Khái niệm số thập phân
1. Ôn lại phân số thập phân
Các phân số có mẫu số là \(10;\,100;\,1000;\,...\) được gọi là các phân số thập phân.
Ví dụ: \(\dfrac{1}{{10}};\,\,\,\,\,\,\,\dfrac{6}{{10}};\,\,\,\,\,\,\,\dfrac{{35}}{{100}};\,\,\,\,\,\,\dfrac{{123}}{{1000}}\) là các phân số thập phân.
2. Khái niệm số thập phân, cấu tạo số thập phân
Khái niệm số thập phân

Các phân số thập phân \(\dfrac{1}{{10}};\,\dfrac{1}{{100}};\,\dfrac{1}{{1000}}\) được viết thành \(0,1;\,\,0,01;\,\,0,001\).
\(0,1\) đọc là: không phẩy một; $0,1 = \dfrac{1}{{10}}$.
\(0,01\) đọc là: không phẩy không một; $0,01 = \dfrac{1}{{100}}$.
\(0,001\) đọc là: không phẩy không không một; $0,001 = \dfrac{1}{{1000}}$.
Các số \(0,1;\,\,\,0,01;\,\,\,0,001\) được gọi là số thập phân.
Tương tự, các phân số thập phân phân \(\dfrac{3}{{10}};\,\dfrac{5}{{100}};\,\dfrac{8}{{1000}}\) được viết thành \(0,3;\,\,0,05;\,\,0,008\).
$\dfrac{3}{{10}} = 0,3;\quad \quad \dfrac{5}{{100}} = 0,05; \quad \quad\dfrac{8}{{1000}} = 0,008$
Các số \(0,3;\,\,\,0,05;\,\,\,0,008\) cũng là số thập phân.

Các số \(3,2;\,\,7,16;\,\,0,241\) cũng là số thập phân.
Cấu tạo số thập phân
Mỗi số thập phân gồm hai phần: phần nguyên và phần thập phân, chúng được phân cách bởi dấu phẩy.
Những chữ số ở bên trái dấu phẩy thuộc về phần nguyên, những chữ số ở bên phải dấu phẩy thuộc về phần thập phân.
Ví dụ:
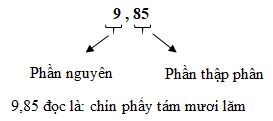
3) Một số dạng bài tập
Dạng 1: Chuyển các phân số thành số thập phân
Phương pháp: Nếu phân số đã cho chưa là phân số thập phân thì ta chuyển các phân số thành phân số thập phân rồi chuyển thành số thập phân.
Ví dụ: Chuyển các phân số sau thành số thập phân:
a) \(\dfrac{7}{{10}}\) b) \(\dfrac{9}{{100}}\)
c) \(\dfrac{2}{5}\) d) \(\dfrac{5}{4}\)
Cách giải:
a) \(\dfrac{7}{{10}} = 0,7\) b) \(\dfrac{9}{{100}} = 0,09\)
c) \(\dfrac{2}{5} = \dfrac{{2 \times 2}}{{5 \times 2}} = \dfrac{4}{{10}} = 0,4\) d) $\dfrac{5}{4} = \dfrac{{5 \times 25}}{{4 \times 25}} = \dfrac{{125}}{{100}} = 1,25$
Mẹo: Khi chuyển phân số thập phân thành số thập phân, ta đếm xem mẫu số có bao nhiêu chữ số \(0\) thì phần thập phân của số thập phân cũng có bấy nhiêu chữ số.
Áp dụng với ví dụ trên:
+) Phân số thập phân \(\dfrac{7}{{10}}\) có \(1\) chữ số \(0\) ở mẫu số nên phần thập phân của số thập phân sẽ có \(1\) chữ số, ta đếm từ phải sang trái, có \(7\)là một chữ số nên ta đặt dấu phẩy trước số \(7\), sau đó thêm \(0\) trước dấu phẩy.
+) Phân số thập phân \(\dfrac{9}{{100}}\) có \(2\) chữ số \(0\) ở mẫu số nên phần thập phân của số thập phân sẽ có \(2\) chữ số, ta đếm từ phải sang trái, có \(9\) là một chữ số nên ta phải thêm \(1\) số \(0\) trước số \(9\) để có đủ \(2\) chữ số rồi đặt dấu phẩy trước số \(0\)vừa thêm, sau đó thêm \(0\) trước dấu phẩy.
Dạng 2: Viết các số đo độ dài, khối lượng ... dưới dạng số thập phân
Phương pháp:
- Tìm mối liên hệ giữa hai đơn vị đo đã cho.
- Chuyển số đo độ dài đã cho thành phân số thập phân có đơn vị đo lớn hơn
- Chuyển từ số đo độ dài dưới dạng phân số thập phân thành số đo độ dài tương ứng dưới dạng số thập phân có đơn vị lớn hơn.
Ví dụ: Điền phân số thập phân và số thập phân thích hợp vào chỗ trống:
a) \(2cm = \dfrac{2}{{10}}dm = ...dm\) b) \(7cm = ...m = ...m\)
Cách giải:
a) \(2cm = \dfrac{2}{{10}}dm = 0,2dm\) b) \(7cm = \dfrac{7}{{100}}m = 0,07m\)
Dạng 3: Viết hỗn số thành số thập phân
Phương pháp: Đổi hỗn số về dạng phân số thập phân, sau đó chuyển thành số thập phân.
Ví dụ: Viết hỗn số sau thành số thập phân:
a) \(3\dfrac{5}{{10}}\) b) \(5\dfrac{7}{{25}}\)
Cách giải:
a) \(3\dfrac{5}{{10}} = \dfrac{{35}}{{10}} = 3,5\) b) \(5\dfrac{7}{{25}} = 5\dfrac{{28}}{{100}} = \dfrac{{528}}{{100}} = 5,28\)
Dạng 4: Chuyển các số thập phân thành phân số thập phân
Phương pháp:
- Phân số thập phân có mẫu số là $10;{\rm{ }}100;{\rm{ }}1000...$
- Nếu phần nguyên của số thập phân bằng \(0\) thì phân số thập phân có tử số nhỏ hơn mẫu số, nếu phần nguyên lớn hơn \(0\) thì tử số lớn hơn mẫu số.
- Số thập phân đã cho ở phần thập phân (bên phải dấu phẩy) có bao nhiêu chữ số thì khi chuyển sang phân số thập phân ở mẫu số cũng sẽ có bấy nhiêu chữ số \(0\).
Ví dụ: Chuyển các số thập phân sau thành phân số thập phân: $0,2;\,\,\,0,09;\,\,\,13,281.$
Cách giải:
$0,2 = \dfrac{2}{{10}};\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,0,09 = \dfrac{9}{{100}};\, \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,13,281 = \dfrac{{13281}}{{1000}}.$
