Chuyển động của hạt mang điện trong từ trường đều

Lý thuyết về chuyển động của hạt mang điện trong từ trường đều môn lý lớp 11 với nhiều dạng bài cùng phương pháp giải nhanh kèm bài tập vận dụng
(387) 1290 29/07/2022
Bài viết đã được lưu
Chia sẻ

Nội dung bài viết

    Xem thêm

    I - NHẬN XÉT

    - Khi hạt điện tích q bay vào trong từ trường thì chịu tác dụng bởi trọng lực với lực lorenxơ nhưng vì \({m_q} \ll \) vì thế có thể bỏ qua trọng lực tác dụng lên điện tích

    => q chỉ chịu tác dụng bởi lực lorenxơ

    - \(\overrightarrow f  \bot \overrightarrow v \) => \(\overrightarrow f \) không sinh công, động năng của hạt được bảo toàn nghĩa là độ lớn vận tốc của hạt không đổi, chuyển động của hạt là chuyển động đều.

    II - CHUYỂN ĐỘNG CỦA HẠT MANG ĐIỆN TRONG TỪ TRƯỜNG ĐỀU

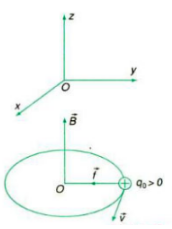
    + Nếu \(\overrightarrow v  \bot \overrightarrow B \) :

    \(\left\{ \begin{array}{l}{f_{{\rm{max}}}} = \left| q \right|vB\\\overrightarrow f  \bot \overrightarrow v \\f = {F_{ht}} \leftrightarrow \left| q \right|vB = m\dfrac{{{v^2}}}{R}\end{array} \right.\)

    => quỹ đạo của q là một chuyển động tròn

    + Nếu \(\overrightarrow v {\rm{//}}\overrightarrow B \):

    \(\overrightarrow f  = \overrightarrow 0 \) => quỹ đạo của q là một đường thẳng

    => q có chuyển động là chuyển động thẳng đều

    + Nếu \(\left( {\overrightarrow v ,\overrightarrow B } \right) = \alpha \):

    => quỹ đạo của q là một đường xoắn ốc bán kính: \(R = \dfrac{{{m_q}v\sin \alpha }}{{\left| q \right|B}}\)

    III - CÁC CÔNG THỨC LIÊN QUAN

    - Định lí động năng: \({A_{ngoailuc}} = \dfrac{{m{v^2}}}{2} - \dfrac{{mv_0^2}}{2} = \left| q \right|U\)

    - Chu kì T(s): \(T = \dfrac{{2\pi R}}{v} = \dfrac{{2\pi }}{\omega }\)  (ω: tốc độ góc (rad/s))

    - Tần số f(Hz) : \(f = \dfrac{1}{T} = \dfrac{\omega }{{2\pi }}\)

    - Công thức liên hệ v-ω: \(v = R\omega \)

    Xem toàn bộ nội dung Vật lý 11:

    (387) 1290 29/07/2022
    Bài viết đã được lưu
    Bài trước
    Chia sẻ
    Bài sau  
    Tìm thêm: Lý thuyết Lý thuyết lớp 11 Vật lý 11