Phương pháp giải các dạng bài tập về quá trình nhân đôi ADN

Phương pháp giải các dạng bài tập về quá trình nhân đôi ADN MÔN SINH Lớp 12 với nhiều phương pháp giải nhanh kèm bài tập vận dụng
(400) 1334 28/07/2022
Bài viết đã được lưu
Chia sẻ

Nội dung bài viết

    Xem thêm

    1. Xác đinh số lần tự nhân đôi, số phân tử ADN và sỗ chuỗi polinucleotit được tạo ra trong quá trình nhân đôi

    a) Tính số phân tử ADN:

    1 ADN mẹ qua 1 lần tự nhân đôi tạo 2= 21 ADN con

    1 ADN mẹ qua 2 lần tự nhân đôi tạo 4= 22 ADN con

    1 ADN mẹ qua 3 lần tự nhân đôi tạo 8= 23 ADN con

    1 ADN mẹ qua k lần tự nhân đôi tạo ra 2k ADN con

    → Qua k lần tự nhân đôi

    $\text{Tổng số ADN tạo thành} = 2^k$

    Trong 2k phân tử ADN tạo thành có một phân tử ADN mẹ ban đầu.

    $\text{Tổng số ADN con} $ $=2^k-1$

    Dù ở đợt tự nhân đôi nào, trong số ADN con tạo ra từ 1 ADN ban đầu, vẫn có 2 ADN con mà mỗi ADN con này có chứa 1 mạch cũ của ADN mẹ. Có nghĩa là luôn có 2 mạch ADN ban đầu.

    Vì vậy số ADN con còn lại có cả 2 mạch có nguyên liệu hoàn toàn từ nucleotit mới của môi trường nội bào. 

    $\text{Số ADN con có 2 mạch mới hoàn toàn} $ $=2^k-2$

    b) Tính số chuỗi polinucleotit.

    Mỗi một phân tử ADN gồm có hai chuỗi polinucleotit. Sau k lần nhân đôi thì số chuỗi polinucleotit được tạo ra là:

    \[2 \times {2^k}\]

    Sau k lần nhân đôi thì số chuỗi polinucleotit có nguyên liệu hoàn toàn từ môi trường được tổng hợp là: 

    \[2 \times \left( {{2^k} - 1} \right)\]

    2. Tính số nucleotit môi trường cung cấp cho quá trình nhân đôi.

    Phân tử ADN mới được tạo ra có thành phần cấu tạo và số lượng các loại nucleotit giống với phân tử ADN ban đầu.

    - Khi gen nhân đôi một lần:

    Nmt = Ngen

    Amt = Tmt = Agen = Tgen

    Gmt = Xmt = Ggen = Xgen

    - Từ đó nếu phân tử ADN nhân đôi k lần thì sẽ có: 

    \[\begin{array}{l}\begin{array}{*{20}{c}}{{N_{mt}} = N \times ({{\bf{2}}^{\bf{k}}} - {\bf{1}})}\\{{A_{mt}} = {T_{mt}} = T \times ({{\bf{2}}^{\bf{k}}} - {\bf{1}}) = A \times ({{\bf{2}}^{\bf{k}}} - {\bf{1}})}\end{array}\\{G_{mt}} = {X_{mt}} = G \times ({{\bf{2}}^{\bf{k}}} - {\bf{1}}) = X \times ({{\bf{2}}^{\bf{k}}} - {\bf{1}})\end{array}\]

    3. Xác định số liên kết hiđrô và liên kết cộng hóa trị được hình thành và bị phá hủy trong nhân đôi.

    a) Tính số liên kết hiđrô (H).

    Số liên kết H trong một phân tử ADN là: 2A + 3G = 2A + 2G + G = N + G

    Số liên kết H được hình thành trong lần nhân đôi thứ k là Hht = H× 2k

    Tổng số liên kết hidro được hình thành sau k lần nhân đôi (bao gồm cả các lần nhân đôi từ 1 → k) là:

    \[\] \(\sum H {\rm{ = }}H \times \left( {{2^1}{\rm{ + }}{2^2}{\rm{ + }}... + {2^k}} \right) = {\bf{2H}} \times ({{\bf{2}}^{\bf{k}}} - {\bf{1}})\)

    Số liên kết H bị phá vỡ là trong lần nhân đôi thứ k là: H = H× 2k – 1

    Tổng số liên kết hidro bị phá vỡ sau k lần nhân đôi là:

    \(\sum H  = H \times \left( {{2^0} + {2^1} + ... + {2^{k - {\rm{ }}1}}} \right) = {\bf{H}} \times ({{\bf{2}}^{\bf{k}}} - {\bf{1}})\)

    b) Tính số liên kết cộng hóa trị

    Liên kết cộng hóa trị giữa các nucleotit trong 1 mạch thì không bị phá vỡ, sau khi nhân đôi thì số lượng liên kết hóa trị tăng lên gấp đôi.

    Sau khi nhân đôi k lần thì số liên kết hóa trị của phân tử là

    \[{\bf{H}}{{\bf{T}}_{{\bf{hinhthanh}}}} = {\bf{HT}} \times \left( {{{\bf{2}}^{\bf{k}}} - {\bf{1}}} \right)\]

    4. Tính số đoạn mồi và đoạn Okazaki xuất hiện trong nhân đôi

    đơn vị tái bản

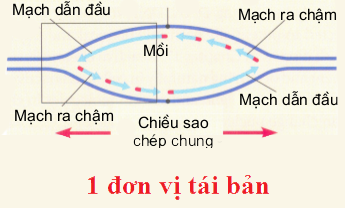
    Xét với một chạc chữ Y:

    Mạch được tổng hợp liên tục có 1 đoạn mồi để khởi đầu, 0 đoạn Okazaki.

    Mạch được tổng hợp gián đoạn có: số đoạn mồi = số đoạn Okazaki

    Trong một đơn vị tái bản thì có hai chạc chữ Y

    → Số đoạn mồi xuất hiện trong một chạc chữ Y là:

    $\text{Số đoạn mồi}$ $=$ $\text{Số đoạn okazaki}$ $+2$

    Xem toàn bộ nội dung Sinh học 12:

    (400) 1334 28/07/2022
    Bài viết đã được lưu
    Bài trước
    Chia sẻ
    Bài sau  
    Tìm thêm: Lý thuyết Lý Thuyết Lớp 12 Sinh học 12