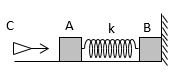
Cho hai vật nhỏ A và B có khối lượng lần lượt là m1 = 900 g, m2 = 4 kg đặt trên mặt phẳng nằm ngang. Hệ số ma sát trượt giữa A, B và mặt phẳng ngang đều là m = 0,1; coi hệ số ma sát nghỉ cực đại bằng hệ số ma sát trượt. Hai vật được nối với nhau bằng một lò xo nhẹ có độ cứng k = 15 N/m; B tựa vào tường thẳng đứng. Ban đầu hai vật nằm yên và lò xo không biến dạng. Vật nhỏ C có khối lượng m = 100 g bay dọc theo trục của lò xo với vận tốc \(\vec{v}\) đến va chạm hoàn toàn mềm với A (sau va chạm C dính liền với A). Bỏ qua thời gian va chạm. Lấy g = 10 m/s2. Giá trị nhỏ nhất của v để B có thể dịch chuyển sang trái là
A. 1,8 m/s
B. 18 m/s
C. 9 m/s
D. 18 cm/s
Lời giải của giáo viên
 HocOn247.com
HocOn247.com
Để B có thể dịch sang trái thì lò xo phải giãn một đoạn ít nhất là xo sao cho:
Fđh = Fms \(\Rightarrow \)kxo = mm2g \(\Rightarrow \)150xo = 40\(\Rightarrow \)\({{\text{x}}_{\text{0}}}=\frac{4}{15}\)m.
Như thế, vận tốc vo mà hệ (m1 + m) có khi bắt đầu chuyển động phải làm cho lò xo có độ co tối đa x sao cho khi nó dãn ra thì độ dãn tối thiểu phải là xo.
Suy ra:
\(\frac{1}{2}k{{x}^{2}}=\mu ({{m}_{1}}+m)g(x+{{x}_{o}})+\frac{1}{2}kx_{o}^{2}\Rightarrow 75{{x}^{2}}-10x-8=0\Rightarrow x=0,4\text{ }m.\)
Theo định luật bảo toàn năng lượng ta có: \(\frac{1}{2}({{m}_{1}}+m)v_{o}^{2}-\frac{1}{2}k{{x}^{2}}=\mu ({{m}_{1}}+m)gx.\)
Từ đó tính được: vo min » 1,8 m/s \(\Rightarrow \)vmin » 18 m/s.
CÂU HỎI CÙNG CHỦ ĐỀ
Điện áp xoay chiều \(u={{U}_{0}}cos\left( 2\pi ft \right)\)V, có \({{U}_{0}}\) không đổi và f thay đổi được vào hai đầu đoạn mạch có R, L, C mắc nối tiếp. Khi \(f={{f}_{0}}\) thì trong đoạn mạch có cộng hưởng điện. Giá trị của \({{f}_{0}}\) là
Một mạch dao động LC lí tưởng đang có dao động điện từ tự do với tần số góc \(\omega \). Gọi \({{q}_{0}}\) là điện tích cực đại của một bản tụ điện thì cường độ dòng điện cực đại trong mạch là
Điện áp \(u={{U}_{0}}cos\left( 100\pi t \right)\) (t tính bằng s) được đặt vào hai đầu đoạn mạch gồm cuộn dây và tụ điện mắc nối tiếp. Cuộn dây có độ tự cảm \(L=\frac{0,15}{\pi }H\) và điện trở \(r=5\sqrt{3}\Omega \), tụ điện có điện dung \(C=\frac{{{10}^{-3}}}{\pi }F\). Tại thời điểm \({{t}_{1}}\)(s) điện áp tức thời hai đầu cuộn dây có giá trị 100 V, đến thời điểm \({{t}_{2}}={{t}_{1}}+\frac{1}{75}s\) thì điện áp tức thời hai đầu tụ điện cũng bằng 100 V. Gía trị của \({{U}_{0}}\) gần đúng là
Hai dao động điều hòa có phương trình dao động lần lượt là \({{x}_{1}}=5cos\left( 2\pi t+\frac{\pi }{6} \right)\)cm và \({{x}_{2}}=5\sqrt{3}cos\left( 2\pi t+\frac{2\pi }{3} \right)\)cm. Biên độ và pha của dao động tổng hợp là
Đoạn mạch MN gồm các phần tử \(R=100\Omega \), \(L=\frac{2}{\pi }H\) và \(C=\frac{100}{\pi }\mu F\) ghép nối điện. Đặt điện áp \(u=220\sqrt{2}cos\left( 100\pi t-\frac{\pi }{4} \right)\)V vào hai đầu đoạn mạch MN. Cường độ dòng điện tức thời qua mạch có biểu thức là
Một vật dao động điều hòa với phương trình dạng cosin. Chọn gốc tính thời gian khi vật đổi chiều chuyển động và khi đó gia tốc của vật đang có giá trị dương. Pha ban đầu là
Cho đoạn mạch LRC. Cuộn dây thuần cảm có cảm kháng . Hệ số công suất của RC bằng hệ số công suất của cả mạch và bằng 0,6. Điện trở thuần có giá trị
Cho đoạn mạch điện trở \(10\Omega \), hiệu điện thế 2 đầu mạch là 20 V. Trong 1 phút điện năng tiêu thụ của mạch là
Để tăng dung kháng của một tụ điện phẳng có điện môi là không khí ta
Cho phản ứng hạt nhân \({}_{1}^{3}H+{}_{1}^{2}H\to {}_{2}^{4}He+{}_{0}^{1}n+17,6MeV\). Năng lượng tỏa ra khi tổng hợp được 1g khí Heli xấp xỉ bằng
Một máy phát điện xoay chiều một pha có phần cảm là roto quay với tốc độ 750 vòng/phút. Tần số của suất điện động cảm ứng là 50 Hz. Số cặp cực của máy phát là
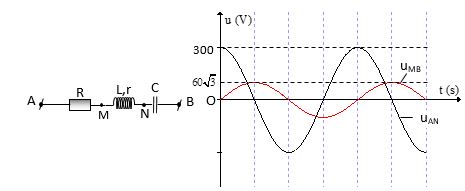
Cho đoạn mạch AB như hình vẽ. Biết R = 80 W, r = 20 W. Đặt vào hai đầu mạch một điện áp xoay chiều \(u\,=\,U\sqrt{2}\cos 100\pi t\text{ }(V).\) Đồ thị biểu diễn sự phụ thuộc của điện áp tức thời giữa hai điểm A, N (uAN) và giữa hai điểm M, B (uMB) theo thời gian được biểu diễn như hình vẽ.
Hệ số công suất của đoạn mạch AB có giá trị gần giá trị nào nhất sau đây?