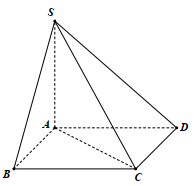
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, \(S A \perp(A B C D) \text { và } S A=a \sqrt{3}\) . Khi đó thể tích của hình chóp S.ABCD bằng:
A. \(\frac{a^{3} \sqrt{3}}{3}\)
B. \(\frac{a^{3} \sqrt{3}}{2}\)
C. \(a^{3} \sqrt{3}\)
D. \(\frac{a^{3} \sqrt{3}}{6}\)
Lời giải của giáo viên
 HocOn247.com
HocOn247.com
Diện tích đáy của hình chóp là \(S_{A B C D}=a^{2}\).
Khi đó \(V_{S . A B CD}=\frac{1}{3} B h=\frac{1}{3} . a^{2}. a \sqrt{3}=\frac{a^{3} \sqrt{3}}{3}\)
CÂU HỎI CÙNG CHỦ ĐỀ
Cho hàm số y=f(x) liên tục trên \(\mathbb{R}\) và có bảng biến thiên như hình vẽ:
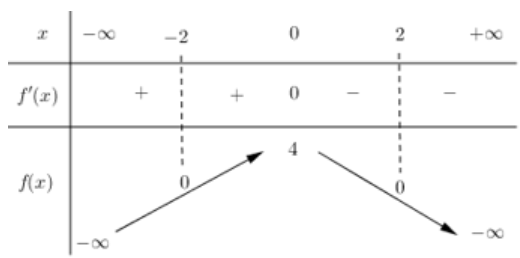
Có bao nhiêu giá trị nguyên của m để phương trình \(f( \sqrt{1+x}-\sqrt{3-x})=f( \sqrt{|m|+1})\) có nghiệm?
Diện tích S của hình phẳng giới hạn bởi các đường \(y=4 x^{2}+x, y=-1, x=0 \text { và } x=1\) được tính bởi công thức nào sau đây?
Xét tích phân \(\int_{1}^{e} \frac{1}{x} \ln x d x . \text { Nếu đặt } \ln x=t \text { thì } \int_{1}^{e} \frac{1}{x} \ln x d x\) bằng:
Số tiệm cận của đồ thị hàm số \(y=\frac{2 x-3}{x+1}\)là:
Có bao nhiêu cặp số nguyên dương \((x ; y)\, với \,x \leq 2020\) thỏa mãn điều kiện \(\log _{2} \frac{x+2}{y+1}+x^{2}+4 x=4 y^{2}+8 y+1\).
Cho hình lập phương ABCD. A' B' C' D' cạnh bằng 3a ,\(K \in C C^{\prime} \text { sao cho } C K=\frac{2}{3} C C^{\prime}\). Mặt phẳng \((\alpha)\) qua A,K và song song với \(B'D'\) chia khối lập phương trình hai phần. Tính thể tích phần khối đa diện chứa đỉnh C.
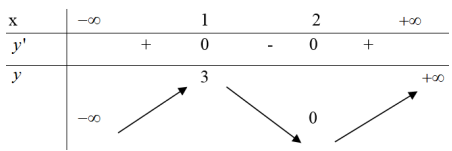
Cho hàm số y=f(x) có bảng biến thiên như hình vẽ. Mệnh đề nào sau đây là sai?
Trong không gian Oxyz , Cho mặt cầu \((S): x^{2}+y^{2}+z^{2}+2 x+2 y-4 z-3=0\). Đường kính của (S) là:
Cho cấp số nhân với \(u_1=3\) và \(u_2 = 9\) . Công bội của cấp số nhân đã cho là:
Trong không gian Oxyz, cho điểm \( M(1 ; 2 ; 3) ; N(-1 ; 1 ; 2)\) Phương trình mặt phẳng trung trực của MN là:
Số giao điểm của đồ thị hàm số \(y=-x^{3}+3 x^{2}-7\) và trục hoành là:
Xét các số thực a, b thỏa mãn: \(\log _{8}\left(4^{a} . 8^{b}\right)=\log _{4} 16\). Mệnh đề nào dưới đây là đúng?
Giá trị nhỏ nhất của hàm số \(f(x)=x^{4}-6 x^{2}-9\) trên đoạn [-1;4] bằng:
Cho lăng trụ tam giác \(A B C \cdot A^{\prime} B^{\prime} C^{\prime} \operatorname{có} B B^{\prime}=a\), góc giữa BB' và mặt phẳng (ABC) bằng \(30^o\). Hình chiếu vuông góc của B' lên mp (ABC) trùng với trọng tâm tam giác ABC. Tính khoảng cách từ A đến mặt phẳng (A'B'C').




