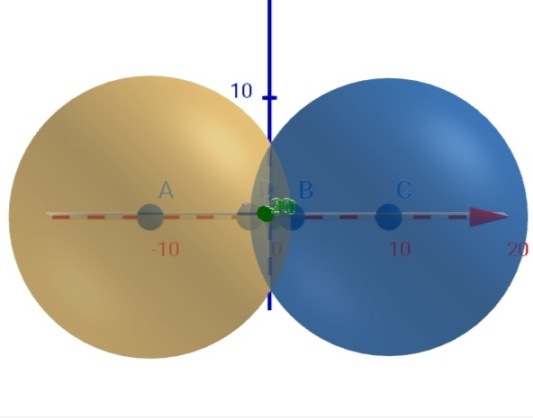
Công ty vàng bạc đá quý muốn làm một món đồ trang sức có hình hai khối cầu bằng nhau giao nhau như hình vẽ. Khối cầu có bán kính 25cm khoảng cách giữa hai tâm khối cầu là 40cm. Giá mạ vàng \(1{{m}^{2}}\) là 470.000 đồng. Nhà sản xuất muốn mạ vàng xung quanh món đồ trang sức đó. Số tiền cần dùng để mạ vàng khối trang sức đó gần nhất với giá trị nào sau đây.
A. 512.000 đồng
B. 664.000 đồng
C. 612.000 đồng
D. 564.000 đồng
Lời giải của giáo viên
 HocOn247.com
HocOn247.com
.png.jpg.png)
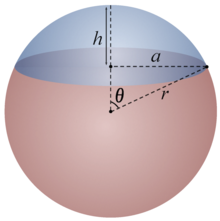
(Phần màu nhạt là phần giao nhau của hai khối cầu)
Gọi h là chiều cao của chỏm cầu. Ta có \(h=\frac{2R-d}{2}=\frac{2.25-40}{2}=5cm\)
(d là khoảng cách giữa hai tâm)
Diện tích xung quanh của chỏm cầu là: \({{S}_{xq}}=2\pi Rh\)
Vì 2 khối cầu bằng nhau nên 2 hình chỏm cầu bằng nhau.
\({{S}_{xq}}\) khối trang sức \(=2{{S}_{xq}}\) khối cầu \(-2{{S}_{xq}}\) chỏm cầu.
Khối trang sức có \({{S}_{xq}}=2.4\pi {{R}^{2}}-2.2\pi Rh=2.4\pi {{.25}^{2}}-2.2\pi .25.5=4500\pi c{{m}^{2}}=0.45{{m}^{2}}\)
Vậy số tiền dùng để mạ vàng khối trang sức đó là \(470.000.0,45\pi \simeq 664.000\) đồng.
CÂU HỎI CÙNG CHỦ ĐỀ
Trong không gian Oxyz, cho mặt cầu \(\left( S \right):{{\left( x-2 \right)}^{2}}+{{\left( y+1 \right)}^{2}}+{{\left( z-1 \right)}^{2}}=9\). Tìm tọa độ tâm I và bán kính R của \(\left( S \right)\) là
Trong không gian với hệ toạ độ Oxyz, viết phương trình mặt phẳng \(\left( \alpha\right)\) chứa trục Ox và đi qua điểm \(M\left( 2;-1;3 \right)\).
Đường tiệm cận ngang của đồ thị hàm số \(y=\frac{3x-2}{x+4}\) là:
Cho số phức \(z=a+bi(a,b\in R)\) thỏa mãn: \(\left| \frac{z-1}{z-i} \right|=1\) và \(\left| \frac{z-3i}{z+i} \right|=1\). Tính 2a+b
Cho hàm số \(y=f\left( x \right)\) có bảng biến thiên như sau
.png)
Hàm số \(y=f\left( x \right)\) nghịch biến trên khoảng nào dưới đây?
Cho hình chóp S.AB có đáy ABC là tam giác vuông cân tại B với AC=a, biết SA vuông góc với mặt phẳng \(\left( ABC \right)\) và SB hợp với \(\left( ABC \right)\) một góc \(60{}^\circ \). Thể tích của khối chóp S.ABC bằng
Cho hàm số \(y=g\left( x \right)\) có bảng biến thiên như sau:
.png)
Điểm cực tiểu của hàm số đã cho là:
Số giao điểm của đồ thị của hàm số \(y={{x}^{3}}-{{x}^{2}}-x-2\) với trục hoành?
Trong không gian với hệ tọa độ Oxyz, cho \(A\left( 1;3;2 \right), B\left( 3;-1;4 \right)\). Tìm tọa độ trung điểm I của AB.
Cho \(\int\limits_{0}^{1}{f\left( x \right)\text{d}x}=-2\) và \(\int\limits_{1}^{5}{\left( 2f\left( x \right) \right)\text{d}x}=6\) khi đó \(\int\limits_{0}^{5}{f\left( x \right)\text{d}x}\) bằng
Trong không gian Oxyz, cho mặt cầu \((S):{{(x-1)}^{2}}+{{(y+1)}^{2}}+{{(z-1)}^{2}}=6\) tâm I. Gọi \((\alpha )\) là mặt phẳng vuông góc với đường thẳng \(d:\frac{x+1}{1}=\frac{y-3}{-4}=\frac{z}{1}\) và cắt mặt cầu (S) theo đường tròn (C) sao cho khối nón có đỉnh I, đáy là đường tròn (C) có thể tích lớn nhất. Biết \((\alpha )\) không đi qua gốc tọa độ, gọi \(H({{x}_{H}},{{y}_{H}},{{z}_{H}})\) là tâm của đường tròn (C). Giá trị của biểu thức \(T={{x}_{H}}+{{y}_{H}}+{{z}_{H}}\) bằng
Tính tích phân \(I=\int\limits_{1}^{2}{\frac{1}{2x-1}\text{d}x}\)
Trong không gian với hệ tọa độ Oxyz, phương trình mặt phẳng vuông góc với đường thẳng \(\frac{x-2}{1}=\frac{y+2}{-2}=\frac{z}{3}\) và đi qua điểm \(A\left( 3;-4;5 \right)\) là
Cho khối trụ có bán kính đáy \(a\sqrt{3}\) và chiều cao \(2a\sqrt{3}\). Thể tích của nó là
Giá trị lớn nhất của hàm số \(f\left( x \right)=-{{x}^{4}}+12{{x}^{2}}+1\) trên đoạn \(\left[ -1;2 \right]\) bằng




