Tiến hành thí nghiệm với 2 con lắc lò xo A và B có quả nặng và chiều dài tự nhiên giống nhau với độ cứng lần lượt là k và 2k. Hai con lắc được treo thẳng đứng vào cùng một giá đỡ. Kéo hai quả nặng đến cùng một vị trí ngang nhau rồi thả nhẹ cùng lúc. Năng lượng dao động của con lắc B gấp 8 lần năng lượng dao động của con lắc A. Gọi tA, tB là khoảng thời gian ngắn nhất kể từ lúc bắt đầu thả hai vật đến khi lực đàn hồi của mỗi con lắc có độ lớn nhỏ nhất. Tỷ số \(\frac{{{t_B}}}{{{t_A}}}\) là:
A. \(\frac{{\sqrt 2 }}{3}\)
B. \(\frac{3}{2}\)
C. \(\frac{{3\sqrt 2 }}{2}\)
D. \(\frac{3}{{2\sqrt 2 }}\)
Lời giải của giáo viên
 HocOn247.com
HocOn247.com
Độ dãn ban đầu của lò xo A là \(\Delta {l_{0A}} = \frac{{mg}}{k}\)
Độ dãn ban đầu của lò xo B là \(\Delta {l_{0B}} = \frac{{mg}}{{2k}} = \frac{1}{2}\Delta {l_{0A}}\)
Áp dụng công thức cơ năng:
\(\left\{ \begin{array}{l}
{{\rm{W}}_A} = \frac{1}{2}.k.A_A^2\\
{{\rm{W}}_B} = \frac{1}{2}.2k.A_B^2
\end{array} \right. \Rightarrow \frac{{{\rm{W}}{}_B}}{{{{\rm{W}}_A}}} = \frac{{2A_B^2}}{{A_A^2}} = 8 \Rightarrow {A_B} = 2{A_A}\)
Từ hình vẽ ta thấy:
\(\begin{array}{l}
\Delta {l_B} + {A_B} = \Delta {l_A} + {A_A} \Leftrightarrow \Delta {l_B} + 2{A_A} = 2\Delta {l_B} + {A_A}\\
\Leftrightarrow {A_A} = \Delta {l_B} = \frac{1}{2}\Delta {l_A} \Rightarrow {A_B} = 2{A_A} = 2\Delta {l_B}
\end{array}\)
Chu kì dao động của con lắc lò xo A:
\({T_A} = 2\pi \sqrt {\frac{m}{k}} \)
Chu kì dao động của con lắc lò xo B:
\({T_B} = 2\pi \sqrt {\frac{m}{{2k}}} = \frac{{{T_A}}}{{\sqrt 2 }}\)
Ta thấy biên độ của A nhỏ hơn độ dãn ban đầu của lò xo, vì vậy lực đàn hồi của lò xo luôn lò là lực kéo và có giá trị nhỏ nhất tại biên âm. Ban đầu vật ở biên dương, nên \({t_A} = \frac{{{T_A}}}{2}\)
Lò xo B có biên độ lớn hơn độ dãn ban đầu, nên lực đàn hồi nhỏ nhất = 0 tại vị trí lò xo không dãn. Ta có VTLG:
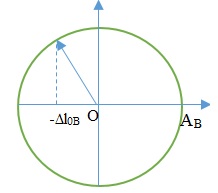
Thời gian:
\({t_B} = \frac{{\frac{\pi }{2} + {\rm{ar}}\cos \frac{{\Delta {l_B}}}{{{A_B}}}}}{{2\pi }}.{T_B} = \frac{{{T_B}}}{3} = \frac{{{T_A}}}{{3\sqrt 2 }}\)
Ta có tỉ số:
\(\frac{{{t_B}}}{{{t_A}}} = \frac{{\frac{{{T_A}}}{{3\sqrt 2 }}}}{{\frac{{{T_A}}}{2}}} = \frac{{\sqrt 2 }}{3}\)
Chọn A.
CÂU HỎI CÙNG CHỦ ĐỀ
Trên một sợi dây đang có sóng dừng. Sóng truyền trên sợi dây có bước sóng λ, khoảng cách giữa hai nút liên tiếp bằng
Vật sáng AB vuông góc với trục chính của thấu kính cho ảnh ngược chiều lớn gấp 4 lần AB và cách AB một khoảng 100cm. Tiêu cự của thấu kính là:
Trong một phản ứng hạt nhân, tổng khối lượng các hạt tham gia sau phản ứng so với trước phản ứng sẽ
Một nguồn có E = 3V, r = 1Ω nối với điện trở ngoài R = 2Ω thành mạch điện kín. Công suất của nguồn điện là:
Trong giao thoa ánh sáng qua hai khe Y-âng, khoảng vân giao thoa bằng i. Nếu đặt toàn bộ thiết bị trong chất lỏng có chiết suất n thì khoảng vân giao thoa sẽ là:
Trong công tác phòng chống dịch bệnh COVID-19 người ta thường dùng nhiệt kế điện tử đo trán để đo thân nhiệt nhằm sàng lọc những người có nguy cơ nhiễm bệnh. Thiết bị này hoạt động dựa trên ứng dụng nào?
.jpg)
Trong dao động cưỡng bức, phát biểu nào sau đây là đúng?
Hai điện tích điểm \({q_1} = + 3\mu C;{q_2} = - 3\mu C\), đặt trong dầu có \(\varepsilon = 2\) cách nhau một khoảng r = 3cm. Lực tương tác giữa hai điện tích đó là:
Đặt điện áp xoay chiều \(u = {U_0}cos\left( {\omega t} \right)\) vào hai đầu đoạn mạch điện chỉ có tụ điện. Nếu điện dung của tụ điện không đổi thì dung kháng của tụ:
Giới hạn quang điện của kẽm là \({\lambda _0} = 0,{35_{}}\mu m\) . Công thoát của electron khỏi kẽm là.
Đặt điện áp xoay chiều có tần số góc 100π rad/s vào hai đầu cuộn cảm thuần có độ tự cảm \(L = \frac{{0,2}}{\pi }H\). Cảm kháng của cuộn dây là
Độ cao là đặc trưng sinh lí của âm, phụ thuộc vào:
Suất điện động \(e = 100\cos \left( {100\pi t + \pi } \right)\left( V \right)\) có giá trị cực đại là:
Một con lắc lò xo dao động với chu kỳ T = 4s. Thời gian ngắn nhất để con lắc đi từ vị trí cân bằng đến biên là:

