Trong thí nghiệm Y-âng về giao thoa ánh sáng, lần thứ nhất, ánh sáng dùng trong thí nghiệm có hai loại bức xạ \({{\lambda }_{1}}=0,56\text{ }\mu \text{m}\) và \({{\lambda }_{2}}\) với \(0,65\text{ }\mu \text{m}<{{\lambda }_{2}}<0,75\text{ }\mu \text{m}\), thì trong khoảng giữa hai vân sáng gần nhau nhất cùng màu với vân sáng trung tâm có 6 vân sáng màu đỏ \({{\lambda }_{2}}\). Lần thứ 2, ánh sáng dùng trong thí nghiệm có 3 loại bức xạ \({{\lambda }_{1}},\text{ }{{\lambda }_{2}}\) và \({{\lambda }_{3}}\), với \({{\lambda }_{3}}=\frac{2}{3}{{\lambda }_{2}}\). Khi đó trong khoảng giữa 2 vân sáng gần nhau nhất và cùng màu với vân sáng trung tâm có bao nhiêu vân sáng màu đỏ?
A. 13
B. 6
C. 7
D. 5
Lời giải của giáo viên
 HocOn247.com
HocOn247.com
Đáp án B
+ Lần thứ nhất: Sử dụng 2 bức xạ \({{\lambda }_{1}}=0,56(\mu m)\) và \({{\lambda }_{2}}\)
Kể luôn 2 vân sáng trùng thì có 8 vân sáng của \({{\lambda }_{2}}\)
→ Vị trí trùng nhau của 2 vân sáng là: \(7{{i}_{2}}\).
Gọi k là số khoảng vân của \({{\lambda }_{1}}$, ta có: $k{{i}_{1}}=7{{i}_{2}}\Leftrightarrow k{{\lambda }_{1}}=7{{\lambda }_{2}}\Rightarrow {{\lambda }_{2}}=\frac{k{{\lambda }_{1}}}{7}\)
\(0,65\text{ }\mu \text{m}<{{\lambda }_{2}}<0,75\text{ }\mu \text{m}\Rightarrow \text{0,65 }\mu \text{m}<\frac{k{{\lambda }_{1}}}{7}<0,75\text{ }\mu \text{m}\Leftrightarrow \text{0,65 }\mu \text{m}<\frac{k.0,56}{7}<0,75\text{ }\mu \text{m}\)
\(\Leftrightarrow 8,125<k<9,375\Rightarrow k=9\Rightarrow {{\lambda }_{2}}=\frac{9.0,56}{7}=0,72\text{ }\mu \text{m}\)
+ Lần thứ 2, sử dụng 3 bức xạ: \({{\lambda }_{1}}=0,56(\mu m);\text{ }{{\lambda }_{2}}=0,72(\mu m);\text{ }{{\lambda }_{3}}=\frac{2}{3}{{\lambda }_{2}}=0,48\text{ }\mu \text{m}\)
Xét vân sáng trùng gần vân sáng trung tâm nhất.
Khi 3 vân sáng trùng nhau \({{x}_{1}}={{x}_{2}}={{x}_{3}}\)
\( \Rightarrow \left\{ \begin{array}{l} \frac{{{k_1}}}{{{k_2}}} = \frac{{{\lambda _2}}}{{{\lambda _1}}} = \frac{9}{7} = \frac{{18}}{{14}}\\ \frac{{{k_2}}}{{{k_3}}} = \frac{{{\lambda _3}}}{{{\lambda _2}}} = \frac{2}{3} = \frac{4}{6} = \frac{6}{9} = \frac{8}{{12}} = \frac{{10}}{{15}} = \frac{{12}}{{18}} = \frac{{14}}{{21}}\\ \frac{{{k_1}}}{{{k_3}}} = \frac{{{\lambda _3}}}{{{\lambda _1}}} = \frac{6}{7} = \frac{{12}}{{14}} = \frac{{18}}{{21}} \end{array} \right. \Rightarrow \left\{ \begin{array}{l} {k_1} = 18\\ {k_2} = 14\\ {k_3} = 21 \end{array} \right.\)
→ Giữa vân trung tâm và vân trùng màu gần vân trung tâm nhất (giữa \({{k}_{2}}=0\) và \({{k}_{2}}=14\)) có 13 vân sáng của bức xạ \({{\lambda }_{2}}\) trong đó có 6 vân trùng màu giữa \({{\lambda }_{2}}\) và \({{\lambda }_{3}}\) (\({{k}_{2}}=2,4,6,8,10,12\)) và 1 vân trùng giữa \({{\lambda }_{1}}\) và \({{\lambda }_{2}}\) (\({{k}_{2}}=7\)).
→ Số vân sáng màu đỏ \({{\lambda }_{2}}\) giữa vân trung tâm và vân trùng màu gần vân trung tâm nhất là: 13-6-1=6 vân.
CÂU HỎI CÙNG CHỦ ĐỀ
Một người cận thị phải đeo kính cận số 0,5 (kính sát mắt). Nếu xem tivi mà không muốn đeo kính, người đó có thể ngồi cách màn hình xa nhất một đoạn là
Cho một sợi dây đang có sóng dừng với tần số góc \(\omega =20\text{ rad/s}\). Tại một điểm A trên dây là một nút sóng, điểm B là bụng sóng gần A nhất, điểm C giữa A và B. Khi sợi dây duỗi thẳng thì khoảng cách AB = 9 cm và AB = 3AC. Khi sợi dây biến dạng nhiều nhất thì khoảng cách giữa A và C là 5 cm. Tốc độ dao động của điểm B khi nó qua vị trí có li độ bằng biên độ của điểm C là
Một chất phóng xạ X có hằng số phóng xạ λ. Ở thời điểm \({{t}_{0}}=0\), có \({{N}_{0}}\) hạt nhân X. Tính từ \({{t}_{0}}\) đến t, số hạt nhân của chất phóng xạ X bị phân rã là
Giả sử hai hạt nhân X và Y có độ hụt khối bằng nhau và số nuclôn của hạt nhân X lớn hơn số nuclôn của hạt nhân Y thì
Điện áp giữa hai cực một vôn kế xoay chiều là \(u=100\sqrt{2}\cos 100\pi t\)(V). Số chỉ của vôn kế là
Cho ba vật dao động điều hòa cùng biên độ A = 10 cm nhưng tần số khác nhau. Biết rằng tại mọi thời điểm, li độ và vận tốc của các vật liên hệ với nhau bởi biểu thức \(\frac{{{x}_{1}}}{{{v}_{1}}}+\frac{{{x}_{2}}}{{{v}_{2}}}=\frac{{{x}_{3}}}{{{v}_{3}}}+2021\). Tại thời điểm t, các vật cách vị trí cân băng của chúng lần lượt là 6 cm, 8 cm và \({{x}_{3}}\). Giá trị \({{x}_{3}}\) gần giá trị nào nhất sau đây?
Hai mạch dao động lí tưởng \(L{{C}_{1}}\) và \(L{{C}_{2}}\) có tần số dao động riêng là \({{f}_{1}}=3f\) và \({{f}_{2}}=4f\). Điện tích trên tụ có giá trị cực đại như nhau và bằng Q. Tại thời điểm dòng điện trong hai mạch dao động có cường độ bằng nhau và bằng 4,8π.f.Q thì tỉ số giữa độ lớn điện tích trên hai tụ \(\frac{{{q}_{2}}}{{{q}_{1}}}\) là
Đặt điện áp \(u=220\sqrt{2}\cos 100\pi t\)(V) vào hai đầu một đoạn mạch gồm điện trở có \(R=50\Omega \), tụ điện có điện dung \(C=\frac{{{10}^{-4}}}{\pi }(F)\) và cuộn cảm thuần có độ tự cảm \(L=\frac{3}{2\pi }(H)\) mắc nối tiếp. Biểu thức của cường độ dòng điện trong mạch là
Một hệ dao động chịu tác dụng của ngoại lực tuần hoàn \({{F}_{n}}={{F}_{0}}\cos \left( 8\pi t+\frac{\pi }{3} \right)\) thì xảy ra hiện tượng cộng hưởng, tần số dao động riêng của hệ phải là
Đồ thị nào sau đây biểu diễn sự phụ thuộc của điện tích của một tụ điện vào hiệu điện thế giữa hai bản của nó?
.jpg)
Điều kiện để hai sóng cơ khi gặp nhau, giao thoa được với nhau là hai sóng phải xuất phát từ hai nguồn dao động
Cho biết \(h=6,{{625.10}^{-34}}J.s,\text{ }c={{3.10}^{8}}m\text{/s}\). Năng lượng photon của tia Rơnghen có bước sóng \({{5.10}^{-11}}m\) là
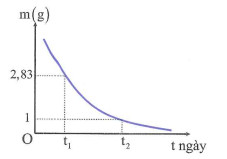
Hình bên là đồ thị biểu diễn khối lượng hạt nhân của một chất phóng xạ X phụ thuộc vào thời gian t. Biết \({{t}_{2}}-{{t}_{1}}=5,7\) ngày. Chu kì bán rã của chất phóng xạ X bằng
Tại một điểm có sóng điện từ truyền qua, cảm ứng từ biến thiên theo phương trình \(B={{B}_{0}}\cos \left( 2\pi {{.10}^{8}}t+\frac{\pi }{3} \right)\) (\({{B}_{0}}>0\), t tính bằng s). Kể từ lúc t = 0, thời điểm đầu tiên để cường độ điện trường tại điểm đó bằng 0 là
Cho mạch điện AMNB, đoạn AM chứa cuộn dây thuần cảm L, đoạn MN chứa điện trở R, đoạn mạch NB chứa tụ điện C. Đặt vào hai đầu AB một điện áp xoay chiều có biểu thức \({{u}_{AB}}=U\sqrt{2}\cos (\omega t)\) V, tần số ω thay đổi được. Khi \(\omega ={{\omega }_{1}}\) thì điện áp giữa hai đầu AN và MB vuông pha nhau, khi đó \({{U}_{AN}}=50\sqrt{5}\)V, \({{U}_{MB}}=100\sqrt{5}\)V. Khi thay đổi tần số góc đến giá trị \(\omega ={{\omega }_{2}}=100\pi \sqrt{2}\)rad/s thì điện áp giữa hai đầu cuộn dây đạt giá trị cực đại. Giá trị của \({{\omega }_{1}}\) là

