Đề thi thử THPT QG năm 2021 môn Vật Lý - Trường THPT Ngô Sỹ Liên
Đề thi thử THPT QG năm 2021 môn Vật Lý
-
Hocon247
-
40 câu hỏi
-
90 phút
-
56 lượt thi
-
Trung bình
Tham gia [ Hs Hocon247.com ] - Cộng Đồng Luyện Thi Trực Tuyến để được học tập những kiến thức bổ ích từ HocOn247.com
Dao động của con lắc đồng hồ là
Dao động của con lắc đồng hồ là dao động duy trì
Máy biến áp là thiết bị có tác dụng
Máy biến áp là thiết bị có khả năng biến đổi điện áp của dòng điện xoay chiều.
Một trong các nguyên tắc chung của việc thông tin liên lạc bằng sóng vô tuyến là phải biến điệu sóng mang. Việc nào dưới đây là thực hiện biến điệu sóng mang?
Thực hiện biến điệu sóng mang: làm sóng cao tần có biên độ biến đổi với tần số âm tần.
Những chất nào sau đây phát ra quang phổ liên tục khi bị nung nóng thích hợp
Những chất phát ra quang phổ liên tục khi bị nung nóng thích hợp là chất rắn, chất lỏng, chất khí có áp suất lớn.
Phát biểu nào về sóng ánh sáng sau đây là không đúng?
Phát biểu không đúng: Bước sóng l’ ánh sáng phát quang bao giờ nhỏ hơn bước sóng l của ánh sáng hấp thụ l’ <l
Quan hệ giữa cường độ điện trường E và hiệu điện thế U giữa hai điểm mà hình chiếu đường nối hai điểm đó lên đường sức là d thì cho bởi biểu thức
Quan hệ giữa cường độ điện trường E và hiệu điện thế U giữa hai điểm mà hình chiếu đường nối hai điểm đó lên đường sức là d thì cho bởi biểu thức: U = E.d.
Đường sức từ không có tính chất nào sau đây?
Đường sức từ không có tính chất : Các đường sức của cùng một từ trường có thể cắt nhau.
Một con lắc lò xo dao động điều hòa với biên độ A =0,03m và có gia tốc cực đại 18m/s2. Biết lò xo của con lắc có độ cứng k = 30N/m. Khối lượng của vật nặng là
amax = ω2.A = kA/m => m = 0,05kg =50g
Một chất điểm dao động điều hòa với tần số góc 10(rad/s). Tại thời điểm ban đầu vật đi qua vị trí có li độ x = 5cm, với tốc độ \(v=50\sqrt{3}\left( cm/s \right)\) theo chiều dương. Phương trình dao động của vật là
Từ đầu bài ta có :
\(\left\{ \begin{align} & A\cos \varphi =5 \\ & -\omega \sin \varphi =50\sqrt{3} \\ \end{align} \right.\)
\(\Rightarrow A=\sqrt{\frac{{{v}^{2}}}{{{\omega }^{2}}}+{{x}^{2}}}=\sqrt{\frac{{{\left( 50\sqrt{3} \right)}^{2}}}{{{10}^{2}}}+{{5}^{2}}}=10\,cm\)
\(\Rightarrow \cos \varphi =\frac{{{x}_{0}}}{A}=\frac{5}{10}=\frac{1}{2}\)
\({{v}_{0}}>0\Rightarrow \varphi =-\arccos \frac{1}{2}=-\frac{\pi }{3}\)
Một sóng cơ có tần số f, truyền trên dây đàn hồi với tốc độ truyền sóng v và bước sóng\(\lambda \). Hệ thức đúng là
Hệ thức đúng là \(v=\frac{\lambda }{f}\)
Dòng điện xoay chiều có biểu thức \(u=220\sqrt{2}\cos (200\pi t)\), t tính bằng s, có điện áp hiệu dụng là bao nhiêu Vôn (V)?
Điện áp hiệu dụng là 100\(\sqrt{2}\)
Số nơtrôn có trong hạt nhân \({}_{11}^{23}Na\) là
Số nơtrôn có trong hạt nhân \({}_{11}^{23}Na\) là 12
Phản ứng hạt nhân nào sau đây không phải là phản ứng nhiệt hạch ?
Phản ứng: \({}_{0}^{1}n+{}_{92}^{235}U={}_{54}^{139}Xe+{}_{38}^{95}Sr+2.{}_{0}^{1}n+200MeV\)
Trong hiện tượng giao thoa sóng trên mặt chất lỏng với hai nguồn có cùng phương trình dao động \({{u}_{O}}=A\cos \omega t\) đặt ở S1, S2. Biết sóng truyền trên mặt nước có bước sóng 4cm. Khoảng cách giữa hai điểm gần nhất mà phần tử nước tại đó dao động với biên độ cực tiểu trên đoạn S1 S2 bằng:
Gọi d là khoảng cách giữa hai điểm gần nhất mà phần tử nước tại đó dao động với biên độ cực tiểu trên đoạn S1 S2:
\(d=\frac{\lambda }{2}=\frac{4}{2}=2cm\)
Đặt điện áp xoay chiều U = 30V vào hai đầu mạch điện không phân nhánh gồm tụ điện và cuộn dây không thuần cảm. .Biết hiệu điện thế 2 đầu tụ điện UC = 40V, hiệu điện thế 2 đầu cuộn dây Udây = 50V. Hệ số công suất của mạch điện là
UC = 40V
\(\begin{align} & {{U}_{day}}=\sqrt{U_{r}^{2}+U_{L}^{2}}=50V \\ & U=\sqrt{U_{r}^{2}+({{U}_{L}}-{{U}_{C}})}=30V \\ \end{align}\)
Từ các phương trình trên ta tìm được UL = 40V, Ur = 30V
Hệ số công suất của mạch điện là: \(\cos \varphi =\frac{{{U}_{r}}}{U}=\frac{30}{30}=1\)
Trong thí nghiệm Y-âng : Hai khe S1 và S2 cách nhau 3mm, hai khe sáng cách màn 2m, bước sóng dùng trong thí nghiệm là 0,6μm thì khoảng cách giữa hai vân tối liên tiếp trên màn là :
Khoảng cách giữa hai vân tối liên tiếp là: \(i=\frac{\lambda D}{a}=\frac{0,6.2}{3}=0,4mm\)
Một tấm kim loại có giới hạn quang điện \({{\lambda }_{o}}=0,35\mu m\), Biết hằng số Plăng h = 6,625.10-34J.s, vận tốc ánh sáng trong chân không c = 3.108 m/s, e = 1,6.10-19 C. Năng lượng cần thiết để gây ra hiện tượng quang điện.
Ta có:
\(\varepsilon =A=\frac{hc}{{{\lambda }_{o}}}=\frac{{{6,625.10}^{-25}}{{.3.10}^{8}}}{{{0,35.10}^{-6}}{{.1,6.10}^{-19}}}=3,55(eV)\)
Hạt nhân càng bền vững khi hạt nhân đó có
Hạt nhân càng bền vững khi hạt nhân đó có năng lượng liên kết riêng càng lớn.
Một khung dây phẳng có diện tích S = 12cm2 đặt trong từ trường đều và có độ lớn B = 5.10-2T. Biết mặt phẳng khung dây hợp với véc tơ cảm ứng từ \(\vec{B}\) một góc 300. Tính từ thông qua khung dây là
Ta có:
\(\Phi =BS\cos \alpha ={{5.10}^{-2}}{{.12.10}^{-2}}.\cos 60={{3.10}^{-5}}Wb\)
Một bức xạ khi truyền trong chân không có bước sóng là\(0,60\mu m\), khi truyền trong thủy tinh có vận tốc là 2.108m/s. Biết chiết suất của thủy tinh đối với bức xạ là 1,5. Tần số của bức xạ là
Ta có:
\(f=\frac{{{v}_{n}}.n}{{{\lambda }_{ck}}}=\frac{{{2.10}^{8}}.1,5}{{{0,6.10}^{-6}}}={{5.10}^{14}}Hz\)
Một sợi dây đàn hổi dài l = 60 cm được treo lơ lửng trên một cần rung. Cần rung có thể dao động theo phương ngang với tần số thay đổi từ 60 Hz đến 180 Hz. Biết tốc độ truyển sóng trên dây là v = 8m/s. Trong quá trình thay đổi thì tần số có bao nhiêu giá trị của tần số có thể tạo ra sóng dừng trên dây:
Phương pháp sử dụng điều kiện có sóng dừng trên dây có 1 đàu là nút một đầu là bụng
Theo bài ra ta có
\(\begin{align} & l=(2k+1)\frac{v}{4f}\Rightarrow f=(2k+1)\frac{v}{4.l}\Rightarrow 60\le (2k+1)\frac{v}{4.l}\le 180 \\ & \Rightarrow \frac{60.2l}{v}-05\le k\le \frac{180.2l}{v}-05\Rightarrow 8,5\le k\le 26,5 \\ \end{align}\)
\(\Rightarrow \) Nghiệm lấy từ ( 9…..26) có 18 giá trị của tần số để có thể tạo ra sóng dừng trên sợi dây
Một mạch dao động gồm tụ điện C = 400 pF và cuộn cảm L = 0,1 mH. Tại thời điểm ban đầu cường độ dòng điện cực đại I\(_{0}\) = 40mA. Nếu điện tích của tụ điện biến thiên theo phương trình q = q\(_{0}\)cos5.10\(^{6}\)t (C) thì cường độ dòng điện trong mạch tại thời điểm đó có biểu thức là:
Ta có:
\(i=\frac{dq}{dt}=-{{q}_{o}}{{.5.10}^{6}}.\sin ({{5.10}^{6}}.t)={{I}_{o}}.\sqrt{LC}{{.5.10}^{6}}\cos ({{5.10}^{6}}+\pi /2)={{4.10}^{-2}}\cos ({{5.10}^{6}}+\pi /2)(A)\)
Hiệu điện thế giữa anốt và catốt của một ống Rơnghen là UAK = 19995V. Động năng ban đầu của các êlectrôn khi bứt ra khỏi catốt là 8.10-19J. Tính bước sóng ngắn nhất của tia X mà ống có thể phát ra.
Ta có:
\({{\varepsilon }_{\max }}=\frac{hc}{{{\lambda }_{\min }}}={{W}_{do}}+\left| e \right|{{U}_{AK}}\Rightarrow {{\lambda }_{\min }}=\frac{hc}{{{W}_{do}}+\left| e \right|{{U}_{AK}}}={{6,211.10}^{-11}}m=62,11pm\)
Nguyên tử hidro gồm một hạt nhân và một electron quay xung quanh nó. Lực tương tác giữa electron và hạt nhân là lực tương tác điện. Biết các hằng số k = 9.109Nm/c2; q = 1,6.10-19C; me = 9,1.10-31kg; h = 6,625.10-34J.s; r0 = 5,3.10-11m. Khi chuyển động trên quỹ đạo N, quãng đường mà êlectrôn đi được là 5,464mm. Tính thời gian êlectrôn chuyển động được quảng đường đó:
Ta có:
\(\begin{align} & v=\sqrt{\frac{k.{{e}^{2}}}{m.16{{r}_{o}}}}=\sqrt{\frac{{{9.10}^{9}}.{{({{1,6.10}^{-19}})}^{2}}}{{{9,1.10}^{-31}}{{.16.5,3.10}^{-11}}}}\approx {{5,464.10}^{5}}m/s \\ & t=\frac{s}{t}=\frac{{{5,464.10}^{-3}}}{{{5,464.10}^{5}}}={{10}^{-8}}s \\ \end{align}\)
Trong chân không, cho hai điện tích \({{q}_{1}}=-{{q}_{2}}={{10}^{-7}}C\) đặt tại hai điểm A và B cách nhau 8cm. Tại điểm C nằm trên đường trung trực của AB và cách AB 3cm người ta đặt điện tích \({{q}_{o}}={{10}^{-7}}C\). Xác định lực điện tổng hợp tác dụng lên qo.
.png)
+ Lực do q1 tác dụng lên qo:
\({{F}_{10}}=k\frac{\left| {{q}_{1}}{{q}_{0}} \right|}{A{{C}^{2}}}={{9.10}^{9}}\frac{\left| {{10}^{-7}}{{.10}^{-7}} \right|}{{{0,05}^{2}}}=0,036N\)
+ Lực do q2 tác dụng lên qo:
\({{F}_{20}}={{F}_{10}}=0,036N\)( do \(\left| {{q}_{1}} \right|=\left| {{q}_{2}} \right|\))
+ Do \({{F}_{20}}={{F}_{10}}\) nên hợp lực Fo tác dụng lên qo:
\( \begin{align} & {{F}_{o}}=2{{F}_{10}}.\cos {{C}_{1}}=2.{{F}_{10}}.\cos A=2.{{F}_{10}}.\frac{AH}{AC} \\ & {{F}_{o}}=2.0,036.\frac{4}{5}={{57,6.10}^{-3}}N \\ \end{align}\)
+ Vậy \({{\vec{F}}_{o}}\) có phương // AB, cùng chiều với vectơ \(\overrightarrow{AB}\) (hình vẽ) và có độ lớn: \({{F}_{o}}={{57,6.10}^{-3}}N\)
Cho mạch điện như hình vẽ. R1 = R2 = RV = 50Ω, ξ = 3V, r = 0.
Bỏ qua điện trở dây nối, số chỉ vôn kế là:
Ta có:
\({{U}_{v}}=\frac{\xi }{{{R}_{1}}+\frac{{{R}_{2}}}{2}+r}.\frac{{{R}_{2}}}{2}=1V\)
Đặt một vật sáng nhỏ vuông góc với trục chính của thấu kính, cách thấu kính 15cm. Thấu kính cho một ảnh ảo lớn gấp hai lần vật. Tiêu cự của thấu kính đó là
Ta có:
\(f=\frac{d.{{d}^{'}}}{d+{{d}^{'}}}=\frac{-2{{d}^{2}}}{-d}=2d=30cm\)
Cho mạch điện như hình vẽ, bỏ qua các điện trở dây nối và ampe kế, ξ = 3V, r = 1Ω, ampe kế chỉ 0,5A. Giá trị của điện trở R là:
Ta có:
\(R=\frac{\xi }{I}-r=5\Omega \)
Hai chất điểm M và N dao động điều hòa dọc theo hai đường thẳng song song nhau và cùng ở sát với trục Ox. Phương trình dao động của chúng lần lượt là \({{x}_{1}}={{A}_{1}}\cos \left( \omega t+\frac{\pi }{3} \right)\,\left( cm \right)\) và \({{x}_{2}}={{A}_{2}}\cos \left( \omega t-\frac{\pi }{6} \right)\,\left( cm \right)\). Biết rằng \(\frac{x_{1}^{2}}{36}+\frac{x_{2}^{2}}{64}=1\). Tại thời điểm t nào đó, chất điểm M có li độ \({{x}_{1}}=-3\sqrt{2}\,cm\) và vận tốc \({{v}_{1}}=60\sqrt{2}\,cm/s\). Khi đó vận tốc tương đối giữa hai chất điểm có độ lớn bằng:
Từ \(\frac{x_{1}^{2}}{36}+\frac{x_{2}^{2}}{64}=1\) ta suy ra được
\(\left\{ \begin{align} & \frac{x_{1}^{2}}{36}\le 1 \\ & \frac{x_{2}^{2}}{64}\le 1 \\ \end{align} \right.\)
\(\Rightarrow \left\{ \begin{align} & -6\le {{x}_{1}}\le 6 \\ & -8\le {{x}_{2}}\le 8 \\ \end{align} \right.\)
\(\Rightarrow \left\{ \begin{align} & {{A}_{1}}=6\left( cm \right) \\ & {{A}_{2}}=8\left( cm \right) \\ \end{align} \right.\)
Ta có:
\(A_{1}^{2}=x_{1}^{2}+\frac{v_{1}^{2}}{{{\omega }^{2}}}\Leftrightarrow {{6}^{2}}={{\left( -3\sqrt{2} \right)}^{2}}+\frac{{{\left( 60\sqrt{2} \right)}^{2}}}{{{\omega }^{2}}}\Rightarrow \omega =20\left( rad/s \right)\)
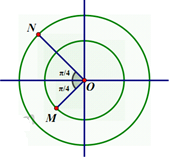
Sử dụng vòng tròn đơn vị: tại thời điểm t, li độ \({{x}_{1}}=\frac{-{{A}_{1}}\sqrt{2}}{2}\)
\({{v}_{1}}>0\)nên ta có điểm M trên hình vẽ. Theo đề bài, N dao động chậm pha hơn M là π/2 nên ta có N như trên hình.
Từ hình vẽ ta suy ra :
\({{x}_{2}}=\frac{-{{A}_{2}}\sqrt{2}}{2}=-4\sqrt{2}\,\left( cm \right)\) và \({{v}_{2}}=\frac{-{{A}_{2}}\omega \sqrt{2}}{2}=-80\sqrt{2}\left( cm/s \right)\)
Vận tốc tương đối:
\(\left| {{v}_{td}} \right|=\left| {{v}_{1}}-{{v}_{2}} \right|=140\sqrt{2}\,\left( cm/s \right)\)
Một chất điểm dao động điều hòa trên trục Ox có vận tốc bằng không tại hai thời điểm liên tiếp t1 = 1,625s và t2 = 2,375s; tốc độ trung bình trong khoảng thời gian đó là 16cm/s. Ở thời điểm t = 0, vận tốc v0 (cm/s) và li độ x0 (cm) của vật thỏa mãn hệ thức:
+ Từ giả thiết ta được \({{t}_{2}}-{{t}_{1}}=0,75s=\frac{T}{2}\Rightarrow T=1,5s\Rightarrow \omega =\frac{4\pi }{3}rad/s\)
+ vtb = 16cm/s nên 2A = 16.0,75 \(\Rightarrow \)A = 6cm
+ Thời điểm \(t=1,625s=\frac{13T}{12}=T+\frac{T}{12}\) giả sử vật ở biên dương, vậy thời điểm t = 0, vật ở vị trí
\(\left\{ \begin{align} & {{x}_{0}}=\frac{6\sqrt{3}}{2}=3\sqrt{3} \\ & {{v}_{0}}=+\frac{{{v}_{\max }}}{2}=4\pi cm/s \\ \end{align} \right.\Rightarrow {{x}_{0}}{{v}_{0}}=12\pi \sqrt{3}\)
Hai chất điểm M và N có cùng khối lượng dao động điều hòa cùng tần số dọc theo hai đường thẳng song song kề nhau và song song với trục tọa độ Ox. Vị trí của M là 6 cm, của N là 8 cm. Trong quá trình dao động khoảng cách lớn nhất giữa M và N theo phương Ox là 10 cm. Mốc thế năng tại vị trí cân bằng. Ở thời điểm mà M có động năng bằng thế năng, tỷ số động năng của M và động năng của N là
Ta có \({{x}_{M}}=6\cos \left( \omega .t+{{\varphi }_{1}} \right);{{x}_{N}}=8\cos \left( \omega .t+{{\varphi }_{2}} \right)\)
Ta có \(x={{x}_{N}}-{{x}_{M}}\)
Biên độ dao động tổng hợp là: \({{A}^{2}}=A_{N}^{2}+A_{M}^{2}\)
Nên 2 dao động vuông pha nhau. Khi M có \({{W}_{d}}={{W}_{t}}=\frac{1}{2}{{W}_{M}}\)
Tức là đang ở vị trí \(x=\pm \frac{A}{\sqrt{2}}\) ứng với \({{\varphi }_{M}}=\frac{\pi }{4}\)
Do 2 dao động vuông pha nên pha dao động của N là \({{\varphi }_{N}}=-\frac{\pi }{4}\)
Nên lúc này vật N cũng có \({{W}_{d}}={{W}_{t}}=\frac{1}{2}{{W}_{N}}\)
Vậy \(\frac{{{W}_{dM}}}{{{W}_{dN}}}=\frac{{{W}_{M}}}{{{W}_{N}}}=\frac{m{{\omega }^{2}}.A_{M}^{2}}{m{{\omega }^{2}}.A_{N}^{2}}=\frac{9}{16}\)
Trên mặt nước có hai nguồn sóng kết hợp A, B cùng pha và cách nhau 6cm, bước sóng λ = 1cm. Xét hai điểm C, D trên mặt nước tạo thành hình vuông ABCD. Số điểm dao động với biên độ cực tiểu trên CD là:
Hai nguồn cùng pha.
Tại M nằm trên CD dao động với biên độ cực tiểu:
\(\begin{align} & CA-CB\le MA-MB=(k+\frac{1}{2})\lambda \le DA-DB \\ & \Leftrightarrow 6-6\sqrt{2}\le (k+\frac{1}{2}).1\le 6\sqrt{2}-6 \\ & \Leftrightarrow -2,9\le k\le 1,9\Rightarrow k=-2;-1;0;1 \\ \end{align}\)
Trên sợi dây nằm ngang đang có sóng dừng ổn định, biên độ dao động của bụng sóng là 2a. Trên dây, cho M, N, P theo thứ tự là ba điểm liên tiếp dao động với cùng biên độ a, cùng pha. Biết MN – NP = 8cm, vận tốc truyền sóng là v = 120cm/s. Tần số dao động của nguồn là
Xét điểm X dao động với biên độ a cách nút sóng gần nhất một đoạn là d
Ta có: \(a=2a\sin \left( \frac{2\pi d}{\lambda } \right)\Rightarrow d=\frac{\lambda }{12}\)
Ba điểm M, N, P được biểu diễn như hình vẽ.
MN – NP = 2λ/3 – λ/3 = λ/3 = 8cm à λ = 24cm
Tần số dao động: f = v/λ = 120/24 = 5Hz
Cho đoạn mạch RLC nối tiếp, R thay đổi được, hiệu điện thế hai đầu đoạn mạch u =60\(\sqrt{2}\(cos100πt (V). Khi R1 = 9Ω hoặc R2 = 16Ω thì công suất trong mạch như nhau. Hỏi với giá trị nào của R thì công suất mạch cực đại, giá trị cực đại đó?
U = 60V; Với hai giá trị R1, R2 của R mạch có cùng công suất P. \({{R}_{1}}+{{R}_{2}}=\frac{{{U}^{2}}}{P}\Rightarrow P=144W\)
Khi R = R0 công suất của mạch cực đại là P0.
Ta có:\({{R}_{0}}=\sqrt{{{R}_{1}}{{R}_{2}}}=12\Omega ;{{R}_{1}}+{{R}_{2}}=\frac{2{{P}_{\max }}}{P}{{R}_{0}}\Rightarrow {{P}_{\max }}=150W\)
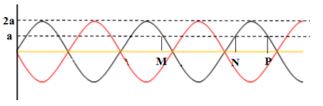
Điện áp xoay chiều giữa hai đầu một đoạn mạch biến đổi điều hòa theo thời gian được mô tả bằng đồ thị hình dưới đây. Biểu thức điện áp tức thời giữa hai đầu đoạn mạch này là
.png)
\(T=0,02s\Rightarrow \omega =100\pi (rad/s)\) và ta có Uo = 200V
Vì u = -Uo/2 = - 100V và đang tiến về biên âm theo chiều âm \(\Rightarrow \varphi =+\frac{2\pi }{3}\)
Người ta cần tải đi một công suất 1 MW từ nhà máy điện về nơi tiêu thụ. Dùng hai công tơ điện đặt ở biến áp tăng thế ở đầu nơi tiêu thụ thì thấy số chỉ chênh lệch mỗi ngày đêm là 216 kWh. Hiệu suất truyền tải điện là
Công suất hao phí:\(\Delta P=\frac{216}{24}=9kW=9000W\)
Hiệu suất truyền tải điện: \(H=\frac{P-\Delta P}{P}=99,1%\)
Đặt điện áp \(u=150\sqrt{2}\cos 100\pi t\,\left( V \right)\) vào hai đầu đoạn mạch AB gồm đoạn AM và MB mắc nối tiếp. Đoạn mạch AM chứa điện trở thuần R không đổi, đoạn mạch MB chứa cuộn cảm thuần có độ tự cảm L không đổi và tụ điện có điện dung C thay đổi được mắc nối tiếp. Ban đầu điện áp hiệu dụng ở hai đầu đoạn mạch AM bằng U1 và điện áp hiệu dụng ở hai đầu đoạn MB là U2. Thay đổi điện dung C của tụ điện đến một giá trị xác định thì thấy điện áp hiệu dụng ở hai đầu đoạn MB bằng \(2\sqrt{2}{{U}_{2}}\) và cường độ dòng điện trong mạch trước và sau khi thay đổi C lệch pha nhau 0,5π. Giá trị của U1 bằng
Gọi \({{\varphi }_{1}},{{\varphi }_{2}}\) lần lượt là độ lệch pha giữa u và i trước và sau khi L thay đổi ta có
\(\tan {{\varphi }_{1}}=\frac{{{U}_{L1}}-{{U}_{C1}}}{{{U}_{R1}}}\)
\(\tan {{\varphi }_{2}}=\frac{{{U}_{L2}}-{{U}_{C2}}}{{{U}_{R2}}}\)
\({{\varphi }_{1}}+{{\varphi }_{2}}=\frac{\pi }{2}\Rightarrow \tan {{\varphi }_{1}}.\tan {{\varphi }_{2}}=-1\)
\({{\left( {{U}_{L1}}-{{U}_{C1}} \right)}^{2}}.{{\left( {{U}_{L2}}-{{U}_{C2}} \right)}^{2}}=U_{R1}^{2}.U_{R2}^{2}\)
\(\Rightarrow {{U}_{MB1}}^{2}.{{U}_{MB2}}^{2}={{U}_{R1}}^{2}.{{U}_{R2}}^{2}\)
\(\Rightarrow 8{{U}_{MB1}}^{2}={{U}_{R1}}^{2}.{{U}_{R2}}^{2}\,\,\left( 1 \right)\)
Mặt khác: \({{U}_{R1}}^{2}+{{U}_{MB1}}^{2}={{U}_{R2}}^{2}+{{U}_{MB2}}^{2}={{U}^{2}}\)
\(\Rightarrow {{U}_{R2}}^{2}={{U}_{R1}}^{2}+{{U}_{MB1}}^{2}-{{U}_{MB2}}^{2}\)
\(\Rightarrow {{U}_{R2}}^{2}={{U}_{R1}}^{2}-7{{U}_{MB1}}^{2}\,\,\,\left( 2 \right)\)
\(\left( 1 \right),\left( 2 \right)\Rightarrow 8{{U}_{MB1}}^{2}={{U}_{R1}}^{2}.\left( {{U}_{R1}}^{2}-7{{U}_{MB1}}^{2} \right)\)
Giải phương trình trùng phương \(\Rightarrow {{U}_{R1}}^{2}=8{{U}_{MB1}}^{2}\,\,\left( 3 \right)\)
Ngoài ra \({{U}_{R1}}^{2}+{{U}_{MB1}}^{2}={{U}^{2}}\,\,\left( 4 \right)\)
Giải \(\left( 3 \right),\left( 4 \right)\Rightarrow {{U}_{R1}}=2.\frac{\sqrt{2}}{3}U=100\sqrt{2}\left( V \right)\).
Trong thí nghiệm Y – âng về giao thoa ánh sáng người ta sử dụng đồng thời ba ánh sáng đơn sắc có bước sóng lần lượt là \({{\lambda }_{1}}=0,48\mu m\) ; \({{\lambda }_{2}}=0,64\mu m\) và \({{\lambda }_{3}}=0,72\mu m\). Số vân sáng đơn sắc quan sát được ở giữa hai vân sáng gần nhất và cùng màu với vân sáng trung tâm là
Ta có : \({{x}_{\equiv }}={{k}_{1}}{{i}_{1}}={{k}_{2}}{{i}_{2}}={{k}_{3}}{{i}_{3}}\)\(\Leftrightarrow \)\(48{{k}_{1}}=64{{k}_{2}}=72{{k}_{3}}\)
BCNN của 48,64,56 là: LCM(LCM( 48,64), 72) = 576
Ta có : \({{k}_{1}}=\frac{576}{48}=12\); \({{k}_{2}}=\frac{576}{64}=9\); \({{k}_{3}}=\frac{576}{72}=8\)
Tổng số vân sáng chưa tính trùng: \(N=\left( {{k}_{1}}-1 \right)+\left( {{k}_{2}}-1 \right)+\left( {{k}_{3}}-1 \right)\) = 11+8+7=26 vân.
. Số vân trùng giữa \({{\lambda }_{1}}\) và \({{\lambda }_{2}}\): \({{k}_{1}}=\frac{4}{3}{{k}_{2}}\)là số từ 1 đến 8 mà chia hết cho 3 có 2 bức xạ.
. Số vân trùng giữa \({{\lambda }_{1}}\) và \({{\lambda }_{3}}\): \({{k}_{1}}=\frac{3}{2}{{k}_{3}}\)là số từ 1 đến 7 mà chia hết cho 2 có 3 bức xạ.
. Số vân trùng giữa \({{\lambda }_{2}}\) và \({{\lambda }_{3}}\): \({{k}_{2}}=\frac{9}{8}{{k}_{3}}\)là số từ 1 đến 7 mà chia hết cho 8 không có bức xạ.
Vậy có \({{N}_{\equiv }}=2+3=5\)\(\Rightarrow \) Số vân thực tế là: N = 26 – 5 = 21 vân.
Trong điều trị bệnh ung thư, bệnh nhân được chiếu xạ với một liều xác định nào đó từ một nguồn phóng xạ. Biết nguồn có chu kỳ bán rã là 4 năm. Khi nguồn được sử dụng lần đầu thì thời gian cho 1 liều xạ là 10 phút. Hỏi sau hai năm thời gian cho 1 liều xạ là bao nhiêu phút
Gọi \(\Delta N\) là liều lượng cho một lần chiếu xạ (\(\Delta N\)= hằng số)
Trong lần chiếu xạ đầu tiên: \(\Delta N={{N}_{01}}\left( 1-{{e}^{-\lambda t1}} \right)\)
Trong lần chiếu xạ tiếp theo sau đó 2 năm: \(\Delta N={{N}_{02}}\left( 1-{{e}^{-\lambda t2}} \right)\)
Với \({{N}_{02}}={{N}_{01}}{{e}^{-\lambda \Delta t}}\) hay \(\Delta N={{N}_{01}}{{e}^{-\lambda \Delta t}}\left( 1-{{e}^{-\lambda t2}} \right)\), (\(\Delta t=2\) năm)
Khi đó ta có: \({{N}_{01}}\left( 1-{{e}^{-\lambda t1}} \right)={{N}_{01}}{{e}^{-\lambda \Delta t}}\left( 1-{{e}^{-\lambda t2}} \right)\)
Với \({{e}^{-\lambda \Delta t}}=\frac{1}{\sqrt{2}}\) và \({{t}_{1}},{{t}_{2}}<<T\) nên \({{e}^{-\lambda t}}\approx 1-\lambda t\)
Ta có: \(\lambda {{t}_{1}}=\frac{1}{\sqrt{2}}\lambda {{t}_{2}}\) suy ra \({{t}_{2}}\approx \sqrt{2}{{t}_{1}}=14,1\) phút
Dùng một hạt α có động năng 4 MeV bắn vào hạt nhân \(_{13}^{27}Al\) đang đứng yên gây ra phản ứng: \(\alpha +_{13}^{27}Al\to _{0}^{1}n+_{15}^{30}P\). Phản ứng này thu năng lượng là 1,2 MeV. Hạt nơtron bay ra theo phương vuông góc với phương bay tới của hạt α. Coi khối lượng của
các hạt nhân bằng số khối (tính theo đơn vị u). Hạt \(_{15}^{30}P\) bay theo phương hợp với phương bay tới của hạt α một góc xấp xỉ bằng:
Có \({{K}_{\alpha }}+1,2={{K}_{n}}+{{K}_{p}}\Rightarrow {{K}_{n}}+{{K}_{p}}=5,2\) (1)
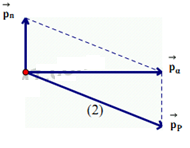
Mặt khác theo giản đồ, ta có
\(p_{P}^{2}=p_{n}^{2}+p_{\alpha }^{2}\Rightarrow {{m}_{P}}{{K}_{p}}={{m}_{n}}{{K}_{n}}+{{m}_{\alpha }}{{K}_{\alpha }}\Rightarrow 30{{K}_{P}}={{K}_{n}}+16\) (2)
Từ (1) và (2) suy ra \({{K}_{n}}=4,5\left( MeV \right)\) và \({{K}_{p}}=0,68\left( MeV \right)\)
Gọi góc giữa hạt P và hạt α là φ, ta có: \(\tan \varphi =\frac{{{p}_{n}}}{{{p}_{\alpha }}}=\sqrt{\frac{{{m}_{n}}{{K}_{n}}}{{{m}_{\alpha }}{{K}_{\alpha }}}}=0,53\Rightarrow \varphi \approx {{28}^{0}}\). Gần với giá trị 300 nhất