Đề thi thử THPT QG năm 2021 môn Vật Lý - Trường THPT Phương Sơn
Đề thi thử THPT QG năm 2021 môn Vật Lý
-
Hocon247
-
40 câu hỏi
-
90 phút
-
56 lượt thi
-
Trung bình
Tham gia [ Hs Hocon247.com ] - Cộng Đồng Luyện Thi Trực Tuyến để được học tập những kiến thức bổ ích từ HocOn247.com
Cho một máy biến áp lý tưởng đang hoạt động ổn định, tần số của điện áp giữa hai đầu cuộn thứ cấp
Máy biến áp là thiết bị dùng để biến đổi biên độ của điện áp xoay chiều, nó hoạt động dựa trên hiện tượng cảm ứng điện từ. Máy biến áp không làm thay đổi tần số của điện áp và dòng điện cho nên tần số của điện áp giữa hai đầu cuộn thứ cấp đúng bằng tần số của điện áp và dòng điện ở cuộn sơ cấp.
Trong dao động cơ điều hòa, những đại lượng nào sau đây có tần số dao động đúng bằng tần số của Li độ?
Phương trình li độ của dao động cơ điều hòa có dạng \(x=Acos\left( \omega t+\varphi \right)\), từ đó ta có thề xác định được:
- Biểu thức vận tốc là \(v={x}'={{v}_{0}}cos\left( \omega t+\varphi +\frac{\pi }{2} \right)\)
- Biểu thức gia tốc là \(a={v}'={{a}_{0}}cos\left( \omega t+\varphi +\pi \right)\)
- Biểu thức lực kéo về là \(F=ma={{F}_{0}}cos\left( \omega t+\varphi +\pi \right)\)
- Biếu thức thế năng là \({{\text{W}}_{t}}=\frac{m{{\omega }^{2}}{{x}^{2}}}{2}=\frac{\text{W}}{2}cos\left( 2\omega t+2\varphi \right)+\frac{\text{W}}{2}\)
- Biểu thức động năng là \({{\text{W}}_{d}}=\frac{m{{v}^{2}}}{2}=-\frac{\text{W}}{2}cos\left( 2\omega t+2\varphi \right)+\frac{\text{W}}{2}\)
- Cơ năng của dao động là một hằng số có biểu thức \(\text{W}=\frac{m{{\omega }^{2}}{{A}^{2}}}{2}\)
Như vậy Vận tốc, Gia tốc và Lực kéo về biến thiên điều hòa với tần số đúng bằng tần số của Li độ dao động.
Trong môi trường chân không, nếu so với ánh sáng trong vùng nhìn thấy thì tia Tử Ngoại có
Trong chân không, tia Tử Ngoại có bước sóng nhỏ hơn bước sóng của ánh sáng Tím (cỡ 380 nm), mà ánh sáng Tím là ánh sáng có bước sóng nhỏ nhất trong vùng nhìn thấy, do đó tia Tử Ngoại có bước sóng nhỏ hơn bước sóng của các ánh sáng trong vùng nhìn thấy.
Khi nói về sóng cơ học, phát biểu nào dưới đây là sai?
Trong quá trình truyền sóng, các phần tử vật chất nơi sóng truyền qua sẽ dao động quanh vị trí cân bằng của nó chứ không truyền đi theo sóng.
Một hạt nhân đang đứng yên thì phóng xạ ra hạt \(\alpha \) và chuyển thành hạt nhân khác. Trong trường hợp này, động năng của hạt \(\alpha \) sinh ra
Phương trình phóng xạ hạt nhân: \({}_{Z}^{A}X={}_{2}^{4}\alpha +{}_{Z-2}^{A-4}Y\)
Áp dụng định luật bảo toàn động lượng ta có \(\overrightarrow{0}={{\overrightarrow{p}}_{\alpha }}+{{\overrightarrow{p}}_{Y}}\)
\(\Rightarrow {{\overrightarrow{p}}_{\alpha }}=-{{\overrightarrow{p}}_{Y}}\Rightarrow p_{\alpha }^{2}=p_{Y}^{2}\Rightarrow {{m}_{\alpha }}{{K}_{\alpha }}={{m}_{Y}}{{K}_{Y}}\)
Do \({{m}_{\alpha }}<{{m}_{Y}}\) ta suy ra \({{K}_{\alpha }}>{{K}_{Y}}\).
Trong dao động cơ học, biên độ của dao động cưỡng bức không phụ thuộc vào
Trong dao động cơ học, biên độ của dao động cưỡng bức có các đặc tính sau:
- Tăng khi biên độ của ngoại lực cưỡng bức tăng.
- Khi tần số ngoại lực càng gần với tần số riêng của vật thì biên độ dao động càng lớn.
- Với cùng một ngoại lực tuần hoàn, nếu lực cản môi trường càng nhỏ thì giá trị cực đại của biên độ càng lớn.
Biên độ của dao động cưỡng bức không phụ thuộc bản chất của ngoại lực cưỡng bức. Dù đó là lực hấp dẫn, lực điện, hay lực từ, ... thì đều có tác dụng cưỡng bức giống nhau.
Khi nói về sóng ánh sáng, phát biểu nào sau đây là đúng?
Thí nghiệm tán sắc ánh sáng mặt trời của Newton qua lăng kính chứng tỏ ánh sáng trắng tự nhiên là sự pha trộn của vô số ánh sáng đơn sắc có màu biến đổi liên tục từ đỏ đến tím. Cần lưu ý là màu sắc của ánh sáng tổng hợp không chỉ phụ thuộc vào sự có mặt của những thành phần đơn sắc nào, mà còn phụ thuộc vào độ mạnh yếu của từng thành phần, do vậy B sai.
Trên sợi dây đàn hồi đang có sóng dừng với C là một điểm trên dây không dao động, khi đó dao động của hai điểm trên dây đối xứng nhau qua C là hai dao động
Dao động của hai điểm đối xứng nhau qua một nút sóng là dao động ngược pha.
Khi nói về cấu tạo của hạt nhân nguyên tử, phát biểu nào là sai?
Trong hạt nhân nguyên tử, hạt prôton mang điện dương (+e) trong khi hạt nơtron không mang điện, do đó điện tích của hạt nhân nguyên tử tính theo đơn vị e (điện tích nguyên tố) đúng bằng tổng số prôton trong hạt nhân.
Cho một mạch đang dao động điện từ LC lý tưởng gồm cuộn dây thuần cảm và một tụ điện. Nếu tăng độ tự cảm của cuộn dây lên gấp đôi và giảm điện dung của tụ điện xuống còn một nửa thì tần số dao động riêng của mạch thay đổi như thế nào?
Tần số dao động của mạch là \(f=\frac{1}{2\pi \sqrt{LC}}\). Nếu độ tự cảm tăng 2 lần và điện dung giảm 2 lần thì tần số sẽ là \(f=\frac{1}{2\pi \sqrt{2L\frac{C}{2}}}=f\), như vậy tần số dao động của mạch không đổi.
Tia bức xạ laze không có đặc điểm nào sau đây?
Tia laze có các đặc tính nổi bật là tính đơn sắc cao, tính định hướng cao, và cường độ lớn. Tuy nhiên, tia laze có bản chất là ánh sáng nên nó bị khúc xạ khi đi qua lăng kính.
Đặc tính nào sau đây của dòng điện xoay chiều là khác với dòng điện không đổi?
Dòng điện xoay chiều có thể chạy qua tụ điện với độ cản trở dòng điện được đặc trưng bởi dung kháng \({{Z}_{C}}=\frac{1}{\omega C}\) , còn dòng điện không đổi thì không thể chạy qua tụ.
Trong mạch dao động LC lý tưởng đang có dao động điện từ với biểu thức điện tích trên tụ là \(q=36cos\left( \frac{{{10}^{6}}}{6}t \right)nC\). Cường độ dòng điện hiệu dụng qua cuộn dây có giá trị là
Ta có cường độ dòng điện hiệu dụng
\(I=\omega Q=\omega \frac{{{Q}_{0}}}{\sqrt{2}}=\frac{{{10}^{6}}}{6}{{.10}^{-9}}.\frac{36}{\sqrt{2}}=3\sqrt{2}{{.10}^{-3}}A=3\sqrt{2}mA\)
Cho dòng điện xoay chiều chạy qua một điện trở thuần có giá trị \(100\,\Omega \) với biểu thức của cường độ dòng điện là \(i=2cos\left( 100\pi t+\frac{\pi }{4} \right)A\) . Giá trị hiệu dụng của hiệu điện thế
Ta có cường độ dòng điện hiệu dụng \(I=\frac{{{I}_{0}}}{\sqrt{2}}=\frac{2}{\sqrt{2}}=\sqrt{2}A\)
Giá trị hiệu dụng của hiệu điện thế \(U=IR=\sqrt{2}.100=100\sqrt{2}\,V\)
Xét trường hợp ánh sáng đỏ có bước sóng là 0,75 μm trong chân không, cho các hằng số \(h={{6,625.10}^{-34}}J.s;\,c={{3.10}^{8}}\,m/s\) và \(e={{1,6.10}^{-19}}C\). Năng lượng phôtôn của ánh sáng này có giá trị bằng
Năng lượng của phôtôn ứng với ánh sáng này là
\(\varepsilon =\frac{hc}{\lambda }=\frac{{{6,625.10}^{-34}}{{.3.10}^{8}}}{{{0,75.10}^{-6}}}={{2,65.10}^{-19}}J\).
Do \(1eV={{1,6.10}^{-19}}J\) nên đổi sang đơn vị eV ta có \(\varepsilon =\frac{{{2,65.10}^{-19}}}{{{1,6.10}^{-19}}}=1,66eV\).
Người ta bắn chùm hạt \(\alpha \) vào hạt nhân \({}_{4}^{9}Be\), phản ứng hạt nhân xảy ra làm xuất hiện một hạt nơtron tự do. Sản phẩm còn lại của phản ứng là
Phương trình hạt nhân \({}_{2}^{4}\alpha +{}_{4}^{9}Be\to {}_{a}^{b}X+{}_{0}^{1}n\).
Áp dụng bảo toàn số khối và bảo toàn điện tích, ta có
\(\left\{ \begin{array}{l}
2 + 4 = a\\
4 + 9 = b + 1
\end{array} \right. \Rightarrow \left\{ \begin{array}{l}
a = 6\\
b = 12
\end{array} \right. \Rightarrow X\)
là cácbon \(\left( {}_{6}^{12}C \right)\)
Chiếu một chùm tia sáng song song hẹp từ không khí tới mặt nước với góc tới là \(60{}^\circ \). Cho chiết suất của nước bằng \(\frac{4}{3}\). Góc hợp bởi tia khúc xạ và tia tới là
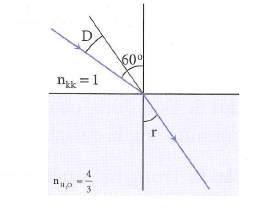
Áp dụng biểu thức định luật khúc xạ ánh sáng có
\(\operatorname{sinr}=\frac{\sin i}{n}=\frac{\sin 60{}^\circ }{\frac{4}{3}}=\frac{3\sqrt{3}}{8}\Rightarrow r=40,5{}^\circ \)
Góc lệch giữa tia tới và tia khúc xạ là
\(D=i-r=60{}^\circ -40,5{}^\circ =19,5{}^\circ \)
Đặt điện áp phương trình \(u={{U}_{0}}cos\left( 100\pi +\frac{\pi }{3} \right)V\) vào giữa hai đầu mạch điện R, L, C mắc nối tiếp thì cường độ dòng điện trong mạch có biểu thức \(i={{I}_{0}}cos\left( 100\pi t+\frac{\pi }{6} \right)\) suất của mạch điện xấp xỉ bằng
Độ lệch pha giữa u và i là \(\varphi ={{\varphi }_{u}}-{{\varphi }_{i}}=\frac{\pi }{3}-\frac{\pi }{6}=\frac{\pi }{6}\).
Hệ số công suất của mạch điện \(k=cos\varphi =cos\frac{\pi }{6}\simeq 0,866\).
Khi một con lắc đơn dao động tự do trong trường trọng lực của trái đất, độ lớn lực căng của sợi dây đạt cực đại khi vật nặng của con lắc đi qua vị trí có
Biểu thức lực căng dây của con lắc đơn
\(T=mg\left( 3cos\alpha -2cos{{\alpha }_{0}} \right)\).
Lực căng đạt cực đại khi \(cos\alpha =1\), khi đó góc lệch của dây treo khỏi phương thẳng đứng là \(\alpha =0\), đây là vị trí mà thành phần lực tác dụng lên vật trên phương tiếp tuyến của quỹ đạo bằng 0 nên gia tốc tiếp tuyến bằng 0.
Trên mặt nước có một nguồn phát sóng dao đông theo phương thẳng đứng với phương trình \(u=5cos\left( 4\pi t-\frac{\pi }{3} \right)\) cm. Sóng truyền trên mặt nước với tốc độ bằng 8 cm/s tới điểm M trên mặt nước cách các nguồn 6 cm. Pha ban đầu của sóng tới tại M bằng
Ta có \(\omega =4\pi \,rad/s\Rightarrow T=0,5s\)
Bước sóng \(\lambda =vT=8.0,5=4cm\)
Phương trình sóng tới tại M là \(u={{A}_{M}}cos\left( 4\pi t-\frac{\pi }{3}-\frac{2\pi {{d}_{M}}}{\lambda } \right)cm\)
Pha ban đầu của sóng tới tại M là \(\varphi =-\frac{\pi }{3}-\frac{2\pi {{d}_{M}}}{\lambda }=-\frac{\pi }{3}-\frac{2\pi .6}{4}=-\frac{10\pi }{3}=-4\pi +\frac{2\pi }{3}\)
Sau khi chuẩn hóa ta có pha ban đầu bằng \(\frac{2\pi }{3}\)
Một ống phát tia X có công suất 400 W đang hoạt động ổn định ở điện áp 10 kV. Cho hằng số \(e={{1,6.10}^{-19}}C\) . Tổng số hạt electron chạy qua ống trong mỗi giây xấp xỉ bằng
Nếu gọi N là số hạt electron chạy qua ống phát tia X trong mỗi giây thì cường độ dòng điện qua ống là \(I=Ne\).
Công suất hoạt động của ống là \(P=UI=UNe\).
Số hạt electron chạy qua ống trong mỗi giây là \(N=\frac{P}{Ue}=\frac{400}{{{10}^{4}}{{.1,6.10}^{-19}}}={{2,5.10}^{17}}\)
Do sự phát bức xạ nên mỗi ngày (86400 s) khối lượng Mặt Trời giảm một lượng \({{3,744.10}^{14}}kg\). Biết vận tốc ánh sáng trong chân không là \({{3.10}^{8}}m/s\). Công suất bức xạ (phát xạ) trung bình của Mặt Trời bằng
Công suất bức xạ trung bình của mặt trời là:
\(P=\frac{E}{t}=\frac{\Delta m{{c}^{2}}}{t}=\frac{{{3,744.10}^{14}}.{{\left( {{3.10}^{8}} \right)}^{2}}}{86400}={{3,9.10}^{26}}\text{W}\)
Biết năng lượng ứng với các trạng thái dừng của nguyên tử Hidro được tính theo biểu thức \({{E}_{n}}=-\frac{{{E}_{0}}}{{{n}^{2}}}\), \({{E}_{0}}\) là hằng số dương, (\(n=1,2,3,...\)). Cho một đám khí Hidro loãng đang ở trạng thái cơ bản. Khi chiếu bức xạ có tần số \({{f}_{1}}\) vào đám nguyên tử này thì chúng chỉ phát ra duy nhất 1 bức xạ đơn sắc. Vậy nếu chiếu bức xạ có tần số \({{f}_{2}}=1,25{{f}_{1}}\) vào đám nguyên tử này thì số bức xạ đơn sắc lớn nhất mà đám khí có thể phát ra là
Do đám khí chỉ phát ra một bức xạ đơn sắc nên bức xạ này tương ứng sự dịch chuyền mức năng lượng \){{E}_{2}}-{{E}_{1}}\), có nghĩa là mức năng lượng kích thích cao nhất của đám khí khi đó là E2, ứng với quỹ đạo L, ta có: \(h{{f}_{1}}={{E}_{2}}-{{E}_{1}}\) (1)
Khi chiếu bức xạ có tần số \({{f}_{2}}=1,25{{f}_{1}}\) thì ta có \(h{{f}_{2}}={{E}_{n}}-{{E}_{1}}\) (2)
Từ (1) và (2) ta có \(\frac{h{{f}_{2}}}{h{{f}_{1}}}=\frac{{{E}_{n}}-{{E}_{1}}}{{{E}_{2}}-{{E}_{1}}}\Rightarrow \frac{-\frac{{{E}_{0}}}{{{n}^{2}}}-\left( -\frac{{{E}_{0}}}{{{1}^{2}}} \right)}{-\frac{{{E}_{0}}}{{{2}^{2}}}-\left( -\frac{{{E}_{0}}}{{{1}^{2}}} \right)}=1,25\)
\(\Rightarrow \frac{-\frac{1}{{{n}^{2}}}+1}{-\frac{1}{{{2}^{2}}}+1}=1,25\Rightarrow n=4\)
Như vậy mức năng lượng kích thích cao nhất trong trường hợp này là mức E4.
Số loại bức xạ do khối khí phát ra là \(N=\frac{4\left( 4-1 \right)}{2}=6\) loại.
Cho mạch điện như hình vẽ. Nguồn điện có suất điện động \(\xi =24V\) và điện trở trong \(r=1\,\Omega \). Trên các bóng đèn Đ1; Đ2 lần lượt có ghi 12V-6W và 12V-12W. Điện trở thuần có giá trị \(R=3\,\Omega \). Cường độ dòng điện chạy qua các bóng đèn có giá trị
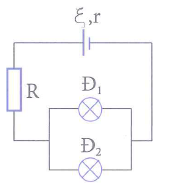
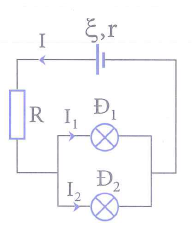
Mỗi bóng đèn dây tóc có bản chất là một điện trở có giá trị R. Nếu Udm và Pdm lần lượt là điện áp định mức và công suất định mức của bóng đèn, khi đó ta có:
\({{P}_{dm}}=\frac{U_{dm}^{2}}{R}\Rightarrow R=\frac{U_{dm}^{2}}{{{P}_{dm}}}\)
Ta có điện trở của mỗi đèn là \({{R}_{d1}}=\frac{{{12}^{2}}}{6}=24\,\Omega \), \({{R}_{d2}}=\frac{{{12}^{2}}}{12}=12\,\Omega \)
Điện trở mạch ngoài là \({{R}_{m}}=R+{{R}_{d12}}=3+8=11\,\Omega \)
Cường độ dòng điện qua mạch chính là \({{I}_{c}}=\frac{\xi }{{{R}_{m}}+r}=\frac{24}{11+1}=2A\)
Hiệu điện thế hai đầu mỗi đèn là \({{U}_{1}}={{U}_{2}}={{U}_{12}}=I.{{R}_{d12}}=2.8=16\,V\)
Cường độ dòng điện qua các bóng đèn là \({{I}_{1}}=\frac{{{U}_{1}}}{{{R}_{d1}}}=\frac{16}{24}=\frac{2}{3}A\) và \({{I}_{2}}=\frac{{{U}_{2}}}{{{R}_{d2}}}=\frac{16}{12}=\frac{4}{3}A\).
Một học sinh thực hiện đo bước sóng của ánh sáng được phát ra từ một nguồn sáng đơn sắc bằng thí nghiệm khe Yâng. Cho số đo khoảng cách giữa hai khe sáng là \(1,00\pm 0,05\) mm và khoảng cách từ mặt phẳng chứa hai khe đến màn là \(2,00\pm 0,01\) m. Trên màn quan sát giao thoa, khoảng cách giữa 10 vân sáng liên tiếp đo được là \(10,80\pm 0,15\) mm. Kết quả biểu diễn bước sóng đo được là
Khoảng cách giữa 10 vân liên tiếp là 9i, ta có \(L=9\frac{\lambda D}{a}\)
\(\Rightarrow \overline{\lambda }=\frac{\overline{aL}}{9\overline{D}}=\frac{1,00.10,80}{9.2,00}=0,60\mu m\)
Sai số của phép đo là \(\Delta \lambda =\overline{\lambda }\left( \frac{\Delta a}{\overline{a}}+\frac{\Delta L}{\overline{L}}+\frac{\Delta D}{\overline{D}} \right)=0,60.\left( \frac{0,05}{1,00}+\frac{0,15}{10,80}+\frac{0,01}{2,00} \right)=0,0413\mu m\)
Theo quy tắc làm tròn sai số, do chữ số có nghĩa đầu tiên lớn hơn 2 nên làm tròn được \(\Delta \lambda =0,04\mu m\)
Từ đó, kết quả làm tròn giá trị trung bình sẽ có hai chữ số có nghĩa, cho nên \(\overline{\lambda }=0,60\mu m\). Suy ra kết quả biểu diễn bước sóng đo được là \(\lambda =0,60\pm 0,04\mu m\)
Đặt điện áp xoay chiều \(u=220\sqrt{2}.cos\left( 100\pi t \right)\) V, với t tính bằng giây, vào hai đầu đoạn mạch gồm điện trở \(R=100\,\Omega \), cuộn cảm thuần \(L=\frac{2}{\pi }H\) và tụ điện \(C=\frac{100}{\pi }\mu F\) mắc nối tiếp. Trong một chu kì của dòng điện, tổng thời gian mà mạch điện sinh công dương là
Trước tiên ta tính được
\(T=\frac{2\pi }{\omega }=\frac{2\pi }{100\pi }=0,02s=20ms\)
\({{Z}_{L}}=\omega L=200\,\Omega $; ${{Z}_{C}}=\frac{1}{\omega C}=100\,\Omega \)
\(\Rightarrow \tan \varphi =\frac{{{Z}_{L}}-{{Z}_{C}}}{R}=\frac{200-100}{100}=1\)
Độ lệch pha giữa u và i là \(\varphi ={{\varphi }_{u}}-{{\varphi }_{i}}=\frac{\pi }{4}\)
Ta có công suất (tiêu thụ điện năng) tức thời trên mạch điện là \(p=ui\).
Để mạch điện sinh công dương thì
\(p = ui < 0 \to \left( \begin{array}{l}
u > 0,{\mkern 1mu} i < 0\\
u < 0,{\mkern 1mu} i > 0
\end{array} \right.\)
tức là u và i phải trái dấu nhau.
Như vậy bài toán đổi thành tính thời gian trong một chu kì, điện áp tức thời giữa hai đầu mạch và cường độ dòng điện tức thời trong mạch trái dấu nhau. Trong trường hợp này, chúng ta sử dụng phương pháp đường tròn hỗn hợp đa trục như hình vẽ. Lấy trục i làm chuẩn trên phương ngang, do u sớm pha \(\frac{\pi }{4}\) so với i nên trục biểu diễn u sẽ lệch \(\frac{\pi }{4}\) theo chiều kim đồng hồ so với trục i.
Dễ thấy khoảng thời gian điện áp hai đầu đoạn mạch sinh công âm ứng với từ M1 tới M2, M3 tới M4, do đó tổng hai góc là \(\Delta \varphi =\frac{\pi }{2}\to \Delta t=\frac{T}{4}={{5.10}^{-3}}s=5ms\).
Hai điện tích điểm \({{q}_{1}}={{2.10}^{-8}}C\) và \({{q}_{2}}=-{{1,8.10}^{-7}}C\) đặt tại hai điểm cố định cách nhau 12 cm trong chân không. Đặt điện tích điểm q3 tại một vị trí sao cho hệ ba điện tích đứng cân bằng. Giá trị của q3 là
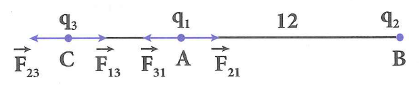
Đề q3 nằm cân bằng thì \({{\overrightarrow{F}}_{13}}=-{{\overrightarrow{F}}_{23}}\), do đó điện tích q3 phải nằm trên đường thẳng nối q1q2 và nằm ngoài ngoài đoạn thẳng q1q2.
Mà \(\left| {{q}_{1}} \right|<\left| {{q}_{2}} \right|\) nên để q3 cân bằng thì q3 phải nằm gần q1 hơn.
Điều kiện đề q3 cân bằng là
\({{F}_{13}}={{F}_{23}}\Rightarrow \frac{k\left| {{q}_{1}}{{q}_{3}} \right|}{C{{A}^{2}}}=\frac{k\left| {{q}_{2}}{{q}_{3}} \right|}{C{{B}^{2}}}\Rightarrow \frac{{{r}_{1}}}{{{r}_{2}}}=\sqrt{\left| \frac{{{q}_{1}}}{{{q}_{2}}} \right|}=\frac{1}{3}\) (1)
Theo bài ra ta có \(CB-CA=12cm\) (2)
Từ (1) và (2) \(\Rightarrow CA=6cm,\,CB=18cm\)
Đề q1 nằm cân bằng thì \({{\overrightarrow{F}}_{21}}=-{{\overrightarrow{F}}_{31}}\Rightarrow {{q}_{3}}<0\) và thỏa mãn \({{F}_{21}}={{F}_{31}}\)
\(\Rightarrow \frac{k\left| {{q}_{1}}{{q}_{2}} \right|}{A{{B}^{2}}}=\frac{k\left| {{q}_{1}}{{q}_{3}} \right|}{C{{A}^{2}}}$$\Rightarrow \left| {{q}_{3}} \right|={{\left( \frac{CA}{AB} \right)}^{2}}.\left| {{q}_{2}} \right|={{\left( \frac{6}{12} \right)}^{2}}.\left| -{{1,8.10}^{-7}} \right|={{45.10}^{-9}}C\)
Như vậy ta có \({{q}_{3}}=-{{4,5.10}^{-8}}C\)
Hai dòng điện không đổi có cường độ \({{I}_{1}}=6A\) và \({{I}_{2}}=9A\) chạy ngược chiều trong hai dây dẫn thẳng, rất dài, song song với nhau và cách nhau 10 cm trong chân không. Cảm ứng từ do hệ hai dòng điện gây ra tại điểm M cách dây dẫn mang dòng điện I1 một đoạn 6 cm và cách dây dẫn mang dòng điện I2 một đoạn 8 cm có độ lớn bằng
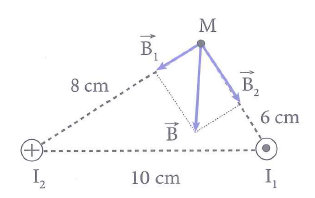
Cảm ứng từ do từng dòng điện I1 và I2 gây ra tại điểm M là
\({{B}_{1}}={{2.10}^{-7}}.\frac{{{i}_{1}}}{{{r}_{1}}}={{2.10}^{-7}}.\frac{6}{0,06}={{2.10}^{-5}}T\)
\({{B}_{2}}={{2.10}^{-7}}.\frac{{{i}_{2}}}{{{r}_{2}}}={{2.10}^{-7}}.\frac{9}{0,08}={{2,25.10}^{-5}}T\)
Do mối liên hệ giữa cách khoảng cách là \({{10}^{2}}={{6}^{2}}+{{8}^{2}}\) thỏa mãn định lý Pitago nên các véc tơ cảm ứng từ tại M vuông góc với nhau, \({{\overrightarrow{B}}_{1}}\bot {{\overrightarrow{B}}_{2}}\).
Suy ra cảm ứng từ tại M là \(B=\sqrt{B_{1}^{2}+B_{2}^{2}}=\sqrt{{{\left( {{2.10}^{-5}} \right)}^{2}}+{{\left( {{2,25.10}^{-5}} \right)}^{2}}}={{3.10}^{-5}}T\) .
Một máy đang phát sóng điện từ ở Hà Nội có phương truyền thẳng đứng hướng lên. Vào một thời điểm, tại điểm M trên phương truyền, véc-tơ cường độ điện trường đang có độ lớn bằng một nửa giá trị cực đại và hướng về phía Nam. Khi đó véc-tơ cảm ứng từ có
Khi đó véc-tơ cảm ứng từ có độ lớn bằng một nửa giá trị cực đại và hướng về phía Đông.
Một con lắc lò xo treo thẳng đứng, đầu trên của lò xo được giữ cố định, đầu dưới gắn với một vật nặng. Khi vật nặng đứng cân bằng thì lò xo giãn 4 cm. Cho \(g=10m/{{s}^{2}}\) và lấy xấp xỉ \({{\pi }^{2}}=10\). Kích thích cho vật dao động điều hòa theo phương thẳng đứng thì thấy trong môt chu kì dao động, khoảng thời gian lò xo bị nén là \(\frac{2}{15}s\). Chọn trục tọa độ trùng với phương dao động của vật, chiều dương hướng xuống dưới, gốc tọa độ tại vị trí cân bằng. Chọn gốc thời gian, t=0, là lúc vật qua vị trí lò xo giãn 8 cm và đang chuyển động chậm dần. Pha ban đầu của dao động là
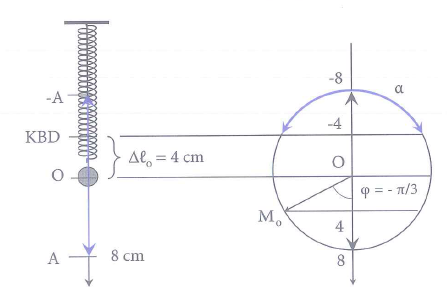
Khi lò xo cân bằng
\({{F}_{dh}}=P\Rightarrow k\Delta \ell =mg\Rightarrow {{\omega }^{2}}=\frac{k}{m}=\frac{g}{\Delta \ell }\)
Chu kì dao động
\(T=2\pi \sqrt{\frac{\Delta \ell }{g}}=2\pi \sqrt{\frac{0,04}{10}}=0,4\left( s \right)\)
Thời gian lò xo nén trong một chu kì là \(\Delta t=\frac{2}{15}=\frac{T}{3}\) tương ứng với một cung \(\alpha =\frac{2\pi }{3}\) trên đường tròn (hình vẽ).
Trong một chu kì dao động, thời gian lò xo bị nén là khoảng thời gian vật đi từ vị trí không biến dạng đến biên âm rồi trở về vị trí không biến dạng, ta có thể suy luận
\(\alpha =\frac{2\pi }{3}rad\Rightarrow \Delta \ell =\frac{A}{2}\Rightarrow A=2\Delta \ell =8\left( cm \right)\)
Khi lò xo giãn 8 cm thì li độ \(x=4cm=\frac{A}{2}\), do vật đang chuyền động chậm dần nên đang đi ra biên dương, như vậy ban đầu vật đang ở vị trí Mo trên đường tròn \(\Rightarrow {{\varphi }_{o}}=-\frac{\pi }{3}rad\)
Một vật dao động điều hòa với tần số f. Chu kì dao động của vật được tính bằng công thức
Chu kì dao động của vật: \(T=\frac{1}{f}\).
Một con lắc lò xo gồm lò xo nhẹ và vật nhỏ có khối lượng m đang dao động điều hòa. Khi vật có tốc độ v thì động năng của con lắc là
Động năng của con lắc là: \({{W}_{}}=\frac{1}{2}m{{v}^{2}}\)
Trong sự truyền sóng cơ, chu kì dao động của một phần tử môi trường có sóng truyền qua được gọi là
Trong sự truyền sóng cơ, chu kì dao động của một phần tử môi trường truyền gọi là chu kì của sóng.
Một sóng âm có chu kì T truyền trong một môi trường với tốc độ v. Bước sóng của sóng âm trong môi trường này là
Bước sóng của sóng âm trong môi trường này: \(\lambda =vT\).
Cường độ dòng điện \(i=2\cos 100\pi t\,\left( A \right)\) (t tình bằng s) có tần số góc bằng
Phương trình của cường độ dòng điện: \(i={{I}_{0}}.\cos \left( \omega t+\varphi \right)=2.\cos 100\pi t\,\left( A \right)\)
Đặt điện áp xoay chiều \(u=60\sqrt{2}\cos 100\pi t\,\left( V \right)\) (t tính bằng s) vào hai đầu đoạn mạch mắc nối tiếp gồm điện trở \(30\Omega \), tụ điện có điện dung \(\frac{{{10}^{-3}}}{4\pi }\) F và cuộn cảm thuần có độ tự cảm L thay đổi được. Điều chỉnh L để cường độ hiệu dụng của dòng điện trong đoạn mạch đạt cực đại. Khi đó, điện áp hiệu dụng giữa hai đầu cuộn cảm là
Dung kháng của tụ điện là:
\({{Z}_{C}}=\frac{1}{2\pi fC}=\frac{1}{2\pi .50.\frac{{{10}^{-3}}}{4\pi }}=40\,\left( \Omega \right)\)
Cường độ dòng điện trong mạch đạt cực đại khi có cộng hưởng:
\(\left\{ \begin{array}{l}
{Z_L} = {Z_C} = 40\left( \Omega \right)\\
{U_R} = U = 60\left( V \right)
\end{array} \right.\)
Cường độ dòng điện trong mạch là:
\(I=\frac{{{U}_{R}}}{R}=\frac{{{U}_{L}}}{{{Z}_{L}}}\Rightarrow \frac{60}{30}=\frac{{{U}_{L}}}{40}\Rightarrow {{U}_{L}}=80\left( V \right)\)
Một con lắc đơn có vật nhỏ mang điện tích dương được treo ở một nơi trên mặt đất trong điện trường đều có cường độ điện trường \(\overrightarrow{E}\). Khi \(\overrightarrow{E}\) hướng thẳng đứng xuống dưới thì con lắc dao động điều hòa với chu kì \({{T}_{1}}\). Khi \(\overrightarrow{E}\) có phương nằm ngang thì con lắc dao động điều hòa với chu kì \({{T}_{2}}\). Biết trong hai trường hợp, độ lớn cường độ điện trường bằng nhau. Tỉ số \(\frac{{{T}_{2}}}{{{T}_{1}}}\) có thể nhận giá trị nào sau đây?
Khi \(\overrightarrow{E}\) hướng thẳng đứng xuống dưới, chu kì của con lắc là: \({{T}_{1}}=2\pi \sqrt{\frac{l}{g+a}}\)
Khi \(\overrightarrow{E}\) có phương nằm ngang , chu kì của con lắc là: \({{T}_{2}}=\sqrt{\frac{l}{\sqrt{{{g}^{2}}+{{a}^{2}}}}}\)
Ta có tỉ số: \(\frac{{{T}_{2}}}{{{T}_{1}}}=\sqrt{\frac{g+a}{\sqrt{{{g}^{2}}+{{a}^{2}}}}}\)
Áp dụng bất đẳng thức Cô – si, ta có:
\({{g}^{2}}+{{a}^{2}}\ge 2ga\) (dấu “=” xảy ra \(\Leftrightarrow g=a\))
\(\Rightarrow 2\left( {{g}^{2}}+{{a}^{2}} \right)\ge {{g}^{2}}+{{a}^{2}}+2ga\Rightarrow 2\left( {{g}^{2}}+{{a}^{2}} \right)\ge {{\left( g+a \right)}^{2}}\)
\(\Rightarrow \frac{{{\left( g+a \right)}^{2}}}{{{g}^{2}}+{{a}^{2}}}\le 2\Rightarrow \sqrt{\frac{g+a}{\sqrt{{{g}^{2}}+{{a}^{2}}}}}\le \sqrt{\sqrt{2}}=1,19\left( 1 \right)\)
Lại có: \(g.a>0\Rightarrow {{g}^{2}}+{{a}^{2}}+2ga>{{g}^{2}}+{{a}^{2}}\)
\(\Rightarrow {{\left( g+a \right)}^{2}}>{{g}^{2}}+{{a}^{2}}\Rightarrow \frac{{{\left( g+a \right)}^{2}}}{\sqrt{{{g}^{2}}+{{a}^{2}}}}>1\,\,\left( 2 \right)\)
Từ (1) và (2), ta có \(\frac{{{T}_{2}}}{{{T}_{1}}}=1,15\) thỏa mãn.
Ở mặt chất lỏng, tại hai điểm A và B có hai nguồn dao động cùng pha theo phương thẳng đứng phát ra hai sóng kết hợp có bước sóng \(\lambda \). Gọi I là trung điểm của đoạn thẳng AB. Ở mặt chất lỏng, gọi \(\left( C \right)\) là hình tròn nhận AB là đường kính, M là một điểm ở ngoài \(\left( C \right)\) gần I nhất mà phần tử chất lỏng ở đó dao động với biên độ cực đại và cùng pha với nguồn. Biết \(AB=6,60\lambda \). Độ dài đoạn thẳng MI có giá trị gần nhất với giá trị nào sau đây?
Độ dài đoạn thẳng MI có giá trị gần nhất với giá trị \(3,31\lambda \).
Cho đoạn mạch AB gồm cuộn cảm thuần L, điện trở \(R=50\Omega \) và tụ điện mắc nối tiếp theo thứ tự đó. Khi đặt vào hai đầu đoạn mạch AB điện áp \(u=100\sqrt{2}\cos 100\pi t\,\left( V \right)\) (t tính bằng s) thì điện áp giữa hai đầu đoạn mạch chứa L và R có biểu thức \({{u}_{LR}}=200\sqrt{2}\cos \left( 100\pi t+\frac{\pi }{3} \right)\,\left( V \right)\). Công suất tiêu thụ của đoạn mạch AB bằng
Hiệu điện thế giữa hai đầu tụ điện là:
\({{u}_{C}}=u-{{u}_{LR}}=100\sqrt{2}\cos 100\pi t-200\sqrt{2}\cos \left( 100\pi t+\frac{\pi }{3} \right)\)
Sử dụng máy tính bỏ túi: \(100\angle 0-200\angle \frac{\pi }{3}=100\sqrt{3}\angle -\frac{\pi }{2}\)
\(\Rightarrow {{u}_{C}}=100\sqrt{6}\cos \left( 100\pi t-\frac{\pi }{2} \right)\left( V \right)\)
Vậy pha ban đầu của dòng điện là: \({{\varphi }_{i}}=0\Rightarrow {{\varphi }_{i}}={{\varphi }_{u}}\)
→ Mạch có cộng hưởng điện: \({{U}_{R}}=U=100\,\left( V \right)\)
Công suất tiêu thụ của đoạn mạch là: \(P=\frac{U_{R}^{2}}{R}=\frac{{{100}^{2}}}{50}=200\,\left( W \right)\)
Trong thí nghiệm về giao thoa sóng ở mặt chất lỏng, tại hai điểm \({{S}_{1}}\) và \({{S}_{2}}\) có hai nguồn dao động cùng pha theo phương thẳng đứng phát ra hai sóng kết hợp với tần số 20 Hz. Ở mặt chất lỏng, tại điểm M cách \({{S}_{1}}\) và \({{S}_{2}}\) lần lượt là 8cm và 15 cm có cực tiểu giao thoa. Biết số cực đại giao thoa trên các đoạn thẳng \(M{{S}_{1}}\) và \(M{{S}_{2}}\) lần lượt là m và \(m+7\). Tốc độ truyền sóng ở mặt chất lỏng là
Số cực đại trên MS1 là m, trên MS2 là m + 7 → số cực đại giữa đường trung trực và M là 3
→ tại M là cực tiểu số 4 (k = 3,5)
Hiệu đường đi tại M là:
\(M{{S}_{2}}-M{{S}_{1}}=3,5\lambda \Rightarrow 15-8=3,5\lambda \Rightarrow \lambda =2\,\left( cm \right)\)
Tốc độ truyền sóng ở mặt chất lỏng là: \(v=\lambda f=2.20=40\,\left( cm/s \right)\)

.JPG)
