Ta có: x = Asinωt => v = ωAcosωt

\(\left\{ \begin{array}{l}
{x_0} = 0\\
{v_0} > 0
\end{array} \right.\) 

Tần số góc của mạch dao động LC:

\(\omega  = \frac{1}{{\sqrt {LC} }}\)

Tia hồng ngoại là những bức xạ có bước sóng lớn hơn 0,76 µm (nằm ngoài vùng ánh sáng nhìn thấy nên không có màu hồng) => C sai 

Vì \(6\left( {cm} \right) \le A \le 18\left( {cm} \right)\) => A không thể bằng 5 cm 

Mạch chỉ có R nên

\(i = \frac{u}{R}i = \frac{{{U_0}}}{R}\)

+ Tính chất sóng của ánh sáng: giao thoa, khúc xạ, phản xạ.

+ Tính chất hạt của ánh sáng: quang điện ngoài, quang điện trong, quang phát quang

Ta có:

\\(\begin{array}{l}
\frac{{{U_2}}}{{{U_1}}} = \frac{{{N_2}}}{{{N_1}}}\\
 \Rightarrow {N_2} = {N_1} = \frac{{{U_2}}}{{{U_1}}} = 2200.\frac{6}{{220}} = 60
\end{array}\\) 

Ta có:

\(\begin{array}{l}
A = \frac{L}{2} = 10\left( {cm} \right)\\
\left\{ \begin{array}{l}
{v_{\max }} = \omega A = 60\left( {cm/s} \right) = 0,6\left( {m/s} \right)\\
{a_{\max }} = {\omega ^2}A = 360\left( {cm/{s^2}} \right) = 3,6\left( {m/{s^2}} \right)
\end{array} \right.
\end{array}\)

+ Công suất hao phí trong quá trình truyền tải:

\(\Delta P = {\left( {\frac{P}{{U\cos \varphi }}} \right)^2}R\)   (*)

+ Dựa vào biểu thức (*) ta thấy biện pháp giảm hao phí trên đường dây tải điện tối ưu nhất là tăng điện áp trước khi truyền tải (sử dụng máy biến áp)

Ta có:

\(v = \sqrt {2g\ell \left( {\cos \alpha  - \cos {\alpha _0}} \right)}  \approx 0,226\left( {m/s} \right)\)

Khi cộng hưởng thì:  

\(\begin{array}{l}
{Z_C} = {Z_L}\\
 \Leftrightarrow \omega L = \frac{1}{{\omega C}} \Leftrightarrow 2\pi fL = \frac{1}{{2\pi fC}}\\
 \Rightarrow L = \frac{1}{{{{\left( {2\pi f} \right)}^2}C}} = \frac{{\sqrt 2 }}{\pi }
\end{array}\)

Ta có:

\(\begin{array}{l}
{v_{\max }} = \omega A = 2v\\
 \Leftrightarrow \omega A = 2\frac{\lambda }{T}\\
 \Leftrightarrow \frac{{2\pi }}{T}A = 2\frac{\lambda }{T} \Rightarrow \lambda  = \pi A
\end{array}\)

Vì hai đầu dây cố định nên: l=kλ/2

Bước sóng sẽ lớn nhất khi k = min = 1 => λ = 2l = 4(m)

Cường độ đòng điện không phụ thuộc vào giới hạn đo của ampe kế. Nếu ampe kế có giới hạn do phù hợp (giới hạn đo phải lớn hơn giá trị cần đo) thì số chỉ ampe kế luôn là giá trị cường độ dòng điện hiệu dụng trong mạch.

Vì hai nguồn cùng pha nên điều kiện cực đại là: d₁ - d₂ = kλ 

Nguyên tắc của mạch chọn sóng trong máy thu thanh dựa trên hiện tượng cộng hưởng điện. Nghĩa là khi máy thu được sóng điện từ thì tần số của mạch dao động trong máy bằng tần số của sóng điện từ thu được lúc đó.

+ Điều kiện để có giao thoa là hai nguồn sóng phải là hai nguồn kết hợp

+ Hai nguồn kết hợp là hai nguồn cùng phương, cùng tần số và có độ lệch pha không đổi theo thời gian 

+ Quang phổ vạch phát xạ của các nguyên tố khác nhau, ở cùng một nhiệt độ thì khác nhau về độ sáng tỉ đối cùa các vạch => A sai

+ Quang phổ vạch phát xạ là một hệ thống những vạch sáng (vạch màu) riêng lẻ, ngăn cách nhau bởi những khoảng tối => B đúng

+ Quang phổ vạch phát xạ do chất khí hay hơi ở áp suất thấp phát ra khi bị kích thích (khi nóng sáng hoặc khi có dòng điện phóng qua) => C sai

+ Đáp án D sai vì thuộc quang phổ liên tục. 

Người ta dựa vào tính chất đâm xuyên và tác dụng lên phim ảnh của tia X để chiếu điện, chụp điện.

Vị trí vân sáng:

\({x_s} = k\frac{{\lambda D}}{a} \Rightarrow {x_{s3}} = 3\frac{{\lambda D}}{a} \Rightarrow \lambda  = 0,4\left( {\mu m} \right)\)

+ Số khối của hạt chì: A = N + Z = 125 + 82 = 207

+ Kí hiệu của hạt nhân Pb là  \(_{82}^{207}Pb\).

Năng lượng phôtôn của bức xạ (I) và bức xạ (II):

\(\left\{ \begin{array}{l}
{\varepsilon _1} = hf = {3,31.10^{ - 19}}J\\
{\varepsilon _2} = \frac{{hc}}{\lambda } = {7,95.10^{ - 19}}J
\end{array} \right.\) 

Điều kiện để xảy ra hiện tượng quang điện là năng lượng hấp thụ được từ phôtôn phải lớn hơn hoặc bằng năng lượng để giải thoát electron (công thoát) => bức xạ II gây ra hiện tượng quang điện, bức xạ I không gây ra hiện tượng quang điện.

+ Pin quang điện là dụng cụ biến quang năng thành điện năng => A sai

+ Quang trở là điện trở có điện trở giảm mạnh khi được chiếu sáng bằng ánh sáng thích hợp => B sai

+ Bước sóng giới hạn của hiện tượng quang điện trong lớn hơn hiện tượng quang điện ngoài vì năng lượng để giải thoát electron khỏi liên kết và trở thành electron dẫn nhỏ hơn năng lượng để bứt electron thoát khỏi kim loại (công thoát electron) => C sai

+ Hiện tượng quang dẫn được giải thích bằng hiện tượng quang điện trong => D đúng.

Đồng vị là những nguyên tử mà hạt nhân có cùng số prôtôn (số Ζ) nhưng khác số nơtron (số N) hay số nuclôn (số khối A = Z + N)

Ta có:

\(\begin{array}{*{20}{l}}
{\varepsilon  = hf = \frac{{hc}}{\lambda } = A + \frac{1}{2}m{v^2}}\\
{ \Rightarrow v = \sqrt {\frac{2}{m}\left( {\frac{{hc}}{\lambda } - A} \right)}  = {{0,73.10}^6}\left( {m/s} \right)}
\end{array}\)

Số hạt còn lại sau thời gian t = 30h:

\(N = {N_0}{2^{ - \frac{t}{T}}} = {N_0}{2^{ - 2}} = \frac{{{N_0}}}{4}\)

Ta có:

\({W_{lk}} = \Delta m{c^2} = \left( {Z.{m_p} + N.{m_n} - m} \right){c^2} = 0,099.931,5 = 92,22MeV\)

Ta có:  

\(\begin{array}{l}
x = k\frac{{\lambda D}}{a}\\
 \Rightarrow \lambda  = \frac{{x.a}}{{kD}} = \frac{5}{k}6,7 \le k \le 12,5\\
 \Rightarrow k = 7,8,9,10,11,12
\end{array}\)

 => có 6 bức xạ.

Vì t = 0 vật ở biên dương nên: x = 13cosωt

+ Vị trí của vật tại thời điểm t cách VTCB đoạn:

\(\left| {{x_1}} \right| = 12 = 13\cos \omega t \Rightarrow \cos \omega t = \frac{{12}}{{13}}\) (1)

+ Vị trí của vật tại thời điểm 2t cách VTCB đoạn:

\(\left| {{x_2}} \right| = 13\cos 2\omega t = 13\left( {2{{\cos }^2}\omega t - 1} \right)\left| {{x_2}} \right| = 13\left[ {2{{\left( {\frac{{12}}{{13}}} \right)}^2} - 1} \right] = 9,15\left( {cm} \right)\)

Năng lượng do nhà máy cung cấp trong thời gian 1 ngày:

\(W = P.t = {1920.10^6}.86400 = {1,66.10^{14}}\left( J \right)\) 

+ Do hiệu suất nhà máy là 30% nên năng lượng do phản ứng hạt nhân cung cấp là:

 \({W_{tp}} = \frac{W}{H} = {5,53.10^{14}}\left( J \right)\)

+ Số phản ứng xảy ra:

 \(n = \frac{{{W_{tp}}}}{{200MeV}} = \frac{{{{5,53.10}^{14}}\left( J \right)}}{{{{200.1,6.10}^{ - 13}}\left( J \right)}} = {1,73.10^{25}}\)

+ Vì một phân hạch ứng với 1 hạt U235 nên số hạt U235 bằng số phản ứng.

+ Do đó khối lượng U235 cần dùng là:

\(m = \frac{{N.A}}{{{N_A}}} = 6746g = 6,746\left( {kg} \right)\)

Biên độ dao động: A = L/2=8/2 = 4(cm)

+ Ta có: 

\(\begin{array}{l}
4\Delta t = \frac{{2T}}{3} \Rightarrow \Delta t = \frac{T}{6}\\
\left| v \right| \ge 8\pi  \Rightarrow \left\{ \begin{array}{l}
v \ge 8\pi \left( {cm/s} \right)\\
v \le  - 8\pi \left( {cm/s} \right)
\end{array} \right.
\end{array}\)

+ Miền thỏa mãn được biểu diễn như hình dưới

\(\begin{array}{l}
 \Rightarrow v = \frac{{{v_{\max }}}}{2} = 8\pi \left( {cm/s} \right)\\
 \Rightarrow {v_{\max }} = 16\pi \left( {cm/s} \right)\\
 \Rightarrow \omega  = \frac{{{v_{\max }}}}{A} = 4\pi \left( {rad/s} \right)\\
W = \frac{1}{2}m{\omega ^2}{A^2} = 0,0128\left( J \right)
\end{array}\)

Khi ω thay đổi để UC = max thì:

\(\begin{array}{l}
{Z_L} = \sqrt {\frac{L}{C} - \frac{{{{\left( {R + r} \right)}^2}}}{2}} \\
 \Rightarrow f = \frac{1}{{2\pi L}}\sqrt {\frac{L}{C} - \frac{{{{\left( {R + r} \right)}^2}}}{2}}  = 61,24\left( {Hz} \right)
\end{array}\)

​

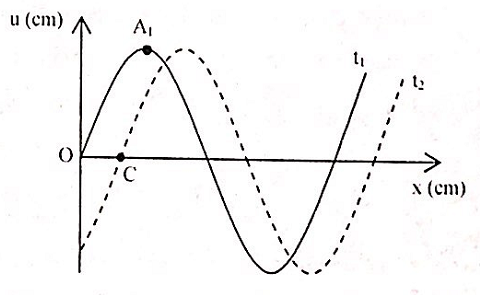
+ Gọi M là hình chiếu của A₁ trên phương truyền sóng (phương Ox).

+ Vì điểm C ở vị trí cân bằng nên:

\(\begin{array}{l}
{v_C} = \omega A \Leftrightarrow \omega A = \frac{\pi }{2}.\frac{\lambda }{T}\\
 \Leftrightarrow \omega A = \frac{\pi }{2}.\frac{{\lambda \omega }}{{2\pi }} \Rightarrow A = \frac{\lambda }{4}
\end{array}\)

+ Trong thời gian Τ/6 sóng truyền pha từ O đến C nên:

\(CO = V.\frac{T}{6} = \frac{\lambda }{6} \Rightarrow CM = \frac{\lambda }{4} - \frac{\lambda }{6} = \frac{\lambda }{{12}}\) 

+ Gọi β là góc tạo A₁CM, ta có: tanβ = \(\frac{{{A_1}M}}{{CM}} = \frac{{\lambda /4}}{{\lambda /12}} = 3 \Rightarrow \beta  = 71,57^\circ \) 

=> A₁CO = 180° - β = 108,43° 

Khi nguyên tử ở trạng thái kích thích chuyển về trạng thái cơ bản có thể phát ra tối đa 15 bức xạ nên n(n-1)/2 = 15 => n = 6 => quỹ đạo P

+ Bước sóng lớn nhất ứng với sự chuyển của electron từ P (n = 6) về O (n = 5):

\(\frac{{hc}}{{{\lambda _{\max }}}} = {E_6} - {E_5} = \frac{{11A}}{{900}}\) 

+ Bước sóng bé nhất ứng với sự chuyển của electron từ P (n = 6) về K (n = 1):

 \(\begin{array}{l}
\frac{{hc}}{{{\lambda _{\min }}}} = {E_6} - {E_1} = \frac{{35A}}{{36}}\\
\frac{{{\lambda _{\max }}}}{{{\lambda _{\min }}}} = \frac{{875}}{{11}} \approx 79,5
\end{array}\)

Khi ω₁ và ω₂ cho cùng U_L thì:

\(Z_{C1}^2 + Z_{C2}^2 = 2Z_x^2\) 

+ Khi ω_L cho U_Lmax thì  

\(\begin{array}{l}
 + Z_C^2 = Z_x^2 \Rightarrow Z_{C1}^2 + Z_{C2}^2 = 2Z_C^2\\
 \Leftrightarrow \frac{1}{{\omega _1^2}} + \frac{1}{{\omega _2^2}} = \frac{2}{{\omega _L^2}}\\
 \Rightarrow {\omega _L} = 48\pi \left( {rad/s} \right)\\
 + Z_C^2 = \frac{L}{C} - \frac{{{R^2}}}{2}\\
 \Leftrightarrow {\left( {\frac{1}{{{\omega _L}C}}} \right)^2} = \frac{L}{C} - \frac{{{R^2}}}{2} \Rightarrow R = 200\Omega \\
 \Rightarrow {U_{L\max }} = \frac{{U\frac{L}{C}}}{{R\sqrt {\frac{L}{C} - \frac{{{R^2}}}{4}} }} = 233,35\left( V \right)
\end{array}\)

+ Bán kính của vệ tinh:

\(v = \omega r = \frac{{2\pi }}{T}.r \Rightarrow r = \frac{{vT}}{{2\pi }} = \frac{{3,07.24.3600}}{{2\pi }} = 42215,53\left( {km} \right)\) 

+ Ta có:

\(\left\{ \begin{array}{l}
{s_{\min }} = r - R = 35815,53\left( {km} \right)\\
{s_{\max }} = \sqrt {{r^2} - {R^2}}  = 41727,58\left( {km} \right)
\end{array} \right.\) 

+ Vậy tỉ số thời gian dài nhất và ngắn nhất là:

\(\frac{{{t_{\max }}}}{{{t_{\min }}}} = \frac{{{s_{\max }}}}{{{s_{\min }}}} = \frac{{41727,58}}{{35815,53}} \approx 1,165\left( s \right)\)

+ Khi 3 bức xạ trùng nhau thì:  

\(\begin{array}{l}
{x_{st}} = {k_1}{i_1} = {k_2}{i_2} = {k_3}{i_3}\\
 \Rightarrow \left\{ \begin{array}{l}
\frac{{{k_1}}}{{{k_2}}} = \frac{9}{8} = \frac{{36}}{{32}}\\
\frac{{{k_3}}}{{{k_2}}} = \frac{{27}}{{32}}
\end{array} \right. \Rightarrow \left\{ \begin{array}{l}
{k_1} = 36n\\
{k_2} = 32n\\
{k_3} = 27n
\end{array} \right.
\end{array}\) (với n là số nguyên)

+ Vì:

\(\begin{array}{l}
{x_M} \le {x_{st}} \le {x_N} \Leftrightarrow  - 14,25 \le 17,28n \le 20,75\\
 \Rightarrow  - 0,82 \le n \le 1,2 \Rightarrow n = 0,1
\end{array}\)

 => Có 2 vị trí

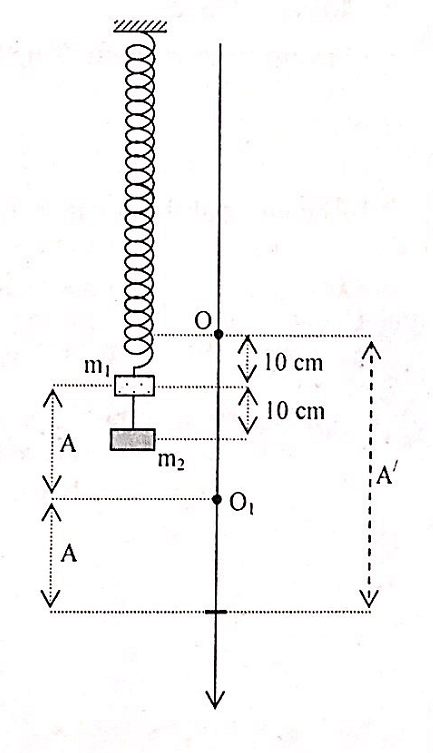
+ Lúc đầu chỉ có m₁, tại VTCB O lò xo dãn 10cm

+ Đưa vật đến vị trí lò xo dãn 20cm thì vật ở dưới VTCB O đoạn x₀ = 10 cm

+ Lúc này gắn thêm m₂ = 3m₁ thì VTCB của hệ bị dịch xuống đoạn: OO₁ = 30 cm

+ Vậy, lúc này hệ ở trên VTCB O₁ đoạn 20cm.

+ Do thả nhẹ nên hệ sẽ dao động với biên độ A = 20cm quanh VTCB O₁.

+ Nhưng khi đến vị trí thấp nhất thì dây đứt, nên VTCB dịch về O.

+ Lúc này m₁ cách O đoạn 50cm và có vận tốc bằng không nên nó sẽ dao động điều hòa quanh O với biên độ A^/ = 50cm.

+ Khi m₁ lên cao nhất thì đã đi được quãng đường s₁ = 2A^/ = 100 cm (kể từ vị trí đứt dây) và mất thời gian:

\(\Delta t = \frac{T}{2} = \frac{{2\pi }}{2}\sqrt {\frac{{\Delta {\ell _0}}}{g}}  = \sqrt {0,1} \left( s \right)\) 

+ Trong thời gian Δt này vật m₂ rơi tự do nên quãng đường m₂ đi được là:

\({s_2} = \frac{1}{2}g\Delta {t^2} = \frac{1}{2}.10.{\left( {\sqrt {0,1} } \right)^2} = 0,5\left( m \right) = 50\left( {cm} \right)\) 

+ Vì dây dài b = 10 cm nên khoảng cách giữa hai vật lúc này là:

\(d = 100 + 10 + 50 = 160\left( {cm} \right) = 1,6\left( m \right)\)

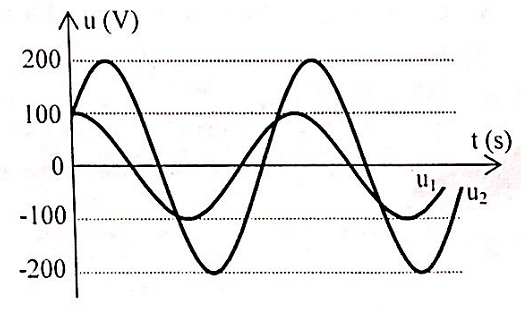
+ Theo đề, ta có:

\({\omega ^2} = \frac{1}{{{L_0}{C_0}}} \Leftrightarrow \omega {L_0} = \frac{1}{{\omega {C_0}}} \Leftrightarrow {Z_L} = {Z_C}\) (1)

+ Từ đồ thị ta viết được biểu thức:

\(\left\{ \begin{array}{l}
{u_1} = 100\cos \omega t\left( V \right)\\
{u_2} = 200\cos \left( {\omega t - \frac{\pi }{3}} \right)\left( V \right)
\end{array} \right.\) 

+ Vì uL và uC ngược pha nên

\(\frac{{{u_L}}}{{{U_{0L}}}} =  - \frac{{{u_C}}}{{{U_{0C}}}} \Leftrightarrow \frac{{{u_L}}}{{{U_L}}} =  - \frac{{{u_C}}}{{{U_C}}}{u_L} =  - {u_C}\)  (2)

+ Lại có:

\(\left\{ \begin{array}{l}
{u_{LX}} = {u_L} + {u_X} = {u_1}\\
{u_{XC}} = {u_X} + {u_C} = {u_2}
\end{array} \right.\left\{ \begin{array}{l}
{u_1} = {u_L} + {u_X}\\
{u_2} = {u_X} - {u_L}
\end{array} \right. \Rightarrow {u_X} = \frac{{{u_1} + {u_2}}}{2}\) 

+ Theo đề, ta có:

\(\begin{array}{l}
{u_X} = \frac{{100 + 200\angle \frac{{ - \pi }}{3}}}{2} = 50\sqrt 7 \angle  - 0,71\\
 \Rightarrow {U_X} = \frac{{{U_{0X}}}}{{\sqrt 2 }} = \frac{{50\sqrt 7 }}{{\sqrt 2 }} = 25\sqrt {14} \left( V \right)
\end{array}\) 

​

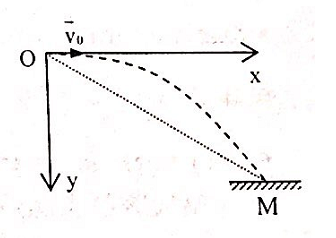
+ Chọn hệ trục tọa độ Oxy có gốc O là vị trí ném, trục Oy hướng xuống

+ Chuyến động của đạn là chuyển động ném ngang với tốc độ ban đầu v0 = 45 (m/s) từ độ cao h = 300 m.

+ Phương trình chuyển động theo các trục: Ox: x = v₀.t

Oy: y = 1/2gt²

+ Khi chạm đất thì: y = h => \(t = \sqrt {\frac{{2h}}{g}}  = \sqrt {\frac{{2.300}}{{10}}}  = 2\sqrt {15} \) (s)

+ Tầm xa khi đó:

\(x = {v_0}t = 45.2\sqrt {15} \left( m \right) = 90\sqrt {15} \left( m \right)\) 

+ Khoảng cách từ vị trí đạn nổ đến vị trí ném:

\(MO = \sqrt {{h^2} + {x^2}}  \approx 459,89\left( m \right)\) 

+ Thời gian truyền âm từ vị trí nổ M đến O là:

\({t_1} = \frac{{MO}}{y} = \frac{{459,89}}{{340}} \approx 1,35\left( s \right)\) 

+ Thời gian nghe được tiếng nổ: Δt = t + t1 = 9,1 (s)