Đề thi thử THPT QG năm 2021 môn Vật Lý - Trường THPT Yên Dũng
Đề thi thử THPT QG năm 2021 môn Vật Lý
-
Hocon247
-
40 câu hỏi
-
90 phút
-
50 lượt thi
-
Trung bình
Tham gia [ Hs Hocon247.com ] - Cộng Đồng Luyện Thi Trực Tuyến để được học tập những kiến thức bổ ích từ HocOn247.com
Một vật dao động điều hoà trong thời gian 1 phút vật thực hiện được 30 dao động. Chu kì dao động của vật là
T = 60/30 = 2s
Một vật nhỏ dao động theo phương trình x = 5cos(wt + 0,25p)(cm). Pha của dao động là
Pha của dao động là 0,125 p
Chọn câu trả lời đúng. Để phân loại sóng ngang hay sóng dọc người ta dựa vào
Để phân loại sóng ngang hay sóng dọc người ta dựa vào phương dao động và phương truyền sóng.
Trong bài hát “Tiếng đàn bầu” do nam ca sĩ Trọng Tấn trình bày có câu “cung thanh là tiếng mẹ, cung trầm là giọng cha…” . “Thanh”,”trầm” trong câu hát này là chỉ đặc tính nào của âm dưới đây?
Trong bài hát “Tiếng đàn bầu” do nam ca sĩ Trọng Tấn trình bày có câu “cung thanh là tiếng mẹ, cung trầm là giọng cha…” . “Thanh”,”trầm” trong câu hát này là chỉ độ cao của âm
Dao động điện từ trong mạch LC tắt càng nhanh khi
Dao động điện từ trong mạch LC tắt càng nhanh khi mạch có điện trở càng lớn.
Đặt điện áp vào hai đầu cuộn dây có độ tự cảm L = 1/π H một điện áp xoay chiều u =141cos100πt V. Cảm kháng của cuộn dây là
Cảm kháng của cuộn dây \({{Z}_{L}}=L\omega =\frac{1}{\pi }100\pi =100\Omega \)
Quang phổ vạch của chất khí loãng có số lượng vạch và vị trí các vạch phụ thuộc vào
Quang phổ vạch của chất khí loãng có số lượng vạch và vị trí các vạch phụ thuộc vào bản chất của chất khí.
Khi nói về ánh sáng đơn sắc, phát biểu nào sau đây đúng?
Ánh sáng đơn sắc không bị tán sắc khi đi qua lăng kính.
Theo mẫu nguyên tử Bo, trạng thái dừng của nguyên tử
Theo mẫu nguyên tử Bo, trạng thái dừng của nguyên tử chỉ là trạng thái cơ bản.
Nội dung chủ yếu của thuyết lượng tử trực tiếp nói về:
Nội dung chủ yếu của thuyết lượng tử trực tiếp nói về sự phát xạ và hấp thụ ánh sáng của nguyên tử, phân tử.
Một vật dao động điều hòa với phương trình x = 2cos(2πt – π/6) cm. Lấy π2= 10. Gia tốc của vật tại thời điểm t = 0,25s là:
x(t=0,25s) = 1cm
\(a=-{{\omega }^{2}}x=40cm/{{s}^{2}}\)
Đồ thị dưới đây biểu diễn x = Acos(wt + j). Phương trình vận tốc dao động là:
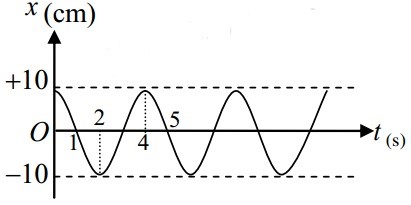
Dựa vào đồ thị tìm được phương trình dao động: x = 10cos(0,5πt)cm
Phương trình vận tốc:v = -5πsin(0,5πt) cm
Cho đoạn mạch gồm điện trở thuần R nối tiếp với tụ điện có điện dung C. Khi dòng điện xoay chiều có tần số góc ω chạy qua thì tổng trở của đoạn mạch là
Khi dòng điện xoay chiều có tần số góc ω chạy qua thì tổng trở của đoạn mạch là \(\sqrt{{{R}^{2}}+{{\left( \frac{1}{\omega C} \right)}^{2}}}\)
Cho điện áp hai đầu đoạn mạch là uAB =120 √2cos(100πt – п/4) V và cường độ dòng điện qua mạch là i = 3 √2cos(100πt + п/12) A. Công suất tiêu thụ trung bình của đoạn mạch là
Ta có:
\(P=UI\cos \varphi =120.3\cos \left( -\frac{\pi }{4}-\frac{\pi }{12} \right)=180W\)
Đặt một điện áp xoay chiều có giá trị tức thời u và giá trị hiệu dụng U vào hai đầu mạch nối tiếp gồm một điện trở thuần R và một tụ điện có điện dung C. Các điện áp tức thời và điện áp hiệu dụng ở hai đầu điện trở và hai đầu tụ điện lần lượt là uR, uC, UR, UC . Hệ thức nào sau đây đúng ?
Hệ thức không đúng là \(U={{U}_{R}}+{{U}_{C}}\)
+ Đoạn mạch RC nối tiếp nên điện áp hai đầu mạch bẳng tổng điện áp thành phần \(u={{u}_{R}}+{{u}_{C}}\)
+ \({{u}_{C}}\bot {{u}_{R}}\Rightarrow \) cống thức độc lập \({{\left( \frac{{{u}_{R}}}{{{U}_{R}}} \right)}^{2}}+{{\left( \frac{{{u}_{C}}}{{{U}_{C}}} \right)}^{2}}=2\)
+ \({{u}_{C}}\bot {{u}_{R}}\Rightarrow {{U}^{2}}=U_{R}^{2}+U_{C}^{2}\)
Trên mặt chất lỏng có hai nguồn sóng kết hợp giống nhau A và B dao động với cùng biên độ 2 cm, cùng tần số 20 Hz, tạo ra trên mặt chất lỏng hai sóng truyền đi với tốc độ 40 cm/s. Điểm M trên mặt chất lỏng cách A đoạn 18 cm và cách B 7 cm có biên độ dao động bằng
Hai nguồn cùng pha \(\Rightarrow {{\varphi }_{A}}={{\varphi }_{B}}=0,{{A}_{1}}={{A}_{2}}=A=2cm\)
Bước sóng: l = = v / f 2cm
Biên độ dao động tổng hợp tại M là:
\({{A}_{M}}=2A\cos \left( \frac{\pi (AM-BM)}{\lambda }+\frac{{{\varphi }_{A}}-{{\varphi }_{B}}}{2} \right)=0\)
Mạch dao động điện từ LC lí tưởng gồm cuộn cảm có độ tự cảm 1mH và tụ điện có điện dung 0,1µF. Dao động điện từ riêng của mạch có chu kì là
Dao động điện từ riêng của mạch có chu kì là 6,28.10-5s.
Trong thí nghiệm Yâng về giao thoa ánh sáng, khoảng cách giữa hai khe là 1mm, khoảng cách từ mặt phẳng chứa hai khe đến màn quan sát là 2m. Nguồn sáng phát ra ánh sáng đơn sắc có bước sóng 0,6 μm. Trên màn, vân sáng thứ ba cách vân trung tâm một khoảng:
Có x = 3t = 3\(\frac{\lambda D}{a}=3,6(mm)\)
Một lăng kính có góc chiết quang A=60, chiết suất của lăng kính đối với tia ló là nđ=1,6444 và đối với tia tím là nt=1,6852. Chiếu tia sáng trắng tới mặt bên của lăng kính dưới góc tới nhỏ. Góc lệch giữa tia ló màu đỏ và tia ló màu tím:
Góc lệch của tia ló màu đỏ: Dđ= (nđ – 1)A; góc lệch của tia ló màu tím: Dt= (nt – 1)A;
Suy ra góc lệch giữa tia đỏ và tím:
D= Dt - Dđ = (nt – nđ)A = (1,6825 – 1,6444).\(\frac{6\pi }{180}\approx 0,0044(rad)\)
Giới hạn quang điện của kim loại đồng là 300 nm. Công thoát electron của kim loại này là
Ta có \(A=\frac{hc}{\lambda }=\frac{{{6,625.10}^{-34}}{{.3.10}^{8}}}{{{300.10}^{-9}}{{.1,6.10}^{-19}}}=4,14eV\)
Chọn câu trả lời đúng. Khối lượng của hạt nhân \({}_{4}^{10}Be\) là 10,0113(u), khối lượng của notron là mn=1,0086u, khối lượng của prôtôn là mp = 1,0072u. Độ hụt khối của hạt nhân \({}_{4}^{10}Be\) là:
Độ hụt khối: \(\Delta m=Z{{m}_{p}}+(A-Z).{{m}_{n}}-{{m}_{hn}}=0,0691u\)
Khi nói về tia β, phát biểu nào sau đây là sai?
Phát biểu sai: Tia β phóng ra từ hạt nhân với tốc độ bằng 2.107 m/s
Chọn câu đúng. Hạt nhân càng bền vững khi có
Hạt nhân càng bền vững khi có năng lượng liên kết riêng càng lớn.
Nếu tăng khoảng cách giữa hai điện tích lên 4 lần thì lực tương tác giữa hai điện tích sẽ :
Nếu tăng khoảng cách giữa hai điện tích lên 4 lần thì lực tương tác giữa hai điện tích sẽ giảm 16 lần
Chọn phương án đúng. Khi một điện tích q = - 2C di chuyển từ điểm M đến điểm N trong điện trường thì lực điện sinh công A = - 6J . Hỏi HĐT UMN là bao nhiêu ?
HĐT UMN là + 3V
Một nguồn âm được coi như một nguồn điểm phát ra sóng âm trong một môi trường coi như không hấp thụ và phản xạ âm thanh. Công suất của nguồn âm là 0,225 W. Cường độ âm chuẩn \({{I}_{0}}={{10}^{-12}}\) \(W/{{m}^{2}}\) . Mức cường độ âm tại một điểm cách nguồn 10 (cm) là
Cường độ ấm tại điểm cách nguồn 10m là \(I=\frac{P}{S}=\frac{0,225}{4.\pi .{{R}^{2}}}=\frac{0,225}{4.\pi {{.10}^{2}}}={{1,79.10}^{-4}}W/{{m}^{2}}\)
Khi đó mức cường độ ấm tại đó là
\(L=\log \frac{I}{{{I}_{0}}}=10\log \left( \frac{{{1,79.10}^{-4}}}{{{10}^{-12}}} \right)=82,53dB\)
Đặt điện áp \(u=U\sqrt{2}\cos \omega t\) (U không đổi, \(\omega \) thay đổi được) vào hai đầu đoạn mạch gồm điện trở thuần R, cuộn cảm thuần có độ tự cảm L và tụ điện có điện dung C mắc nối tiếp. Trên hình vẽ, các đường (1),(2) và (3) là đồ thị của các điện áp hiệu dụng ở hai đầu điện trở \({{\text{U}}_{\text{R}}}\), hai đầu tụ điện \({{\text{U}}_{\text{C}}}\) và hai đầu cuộn cảm \({{\text{U}}_{\text{L}}}\) theo tần số góc \(\omega \). Đường (1),(2) và (3) theo thứ tự tương ứng là
.png)
Quan sát đồ thị ta thấy khi tần số bằng 0 thì nguồn coi như là nguồn 1 chiều. Khi đó chỉ có điện trở hoạt động. Vậy đường số 1 tương ứng với điện trở.
Xét nguyên tử hiđrô theo mẫu nguyên tử Bo. Gọi F là độ lớn lực tương tác điện giữa êlectron và hạt nhân khi êlectron chuyển động trên quỹ đạo dừng K. Khi độ lớn lực tương tác điện giữa êlectron và hạt nhân là \(\frac{\text{F}}{\text{16}}\) thì êlectron đang chuyển động trên quỹ đạo dừng nào?
Lực điện + trên quỹ đạo K :\(F=\frac{k{{e}^{2}}}{{{r}_{0}}^{2}}\)
+ khi lực điện là \(Fn=\frac{F}{16}\Leftrightarrow \frac{k{{e}^{2}}}{{{r}_{n}}^{2}}=\frac{k{{e}^{2}}}{16{{r}_{0}}^{2}}\to {{r}_{n}}=4{{r}_{0}}={{n}^{2}}{{r}_{0}}\to n=2\)
Tương ứng với quỹ đạo L
Một chất phóng xạ có chu kỳ bán rã ℓà 200 ngày, tại thời điểm t ℓượng chất còn ℓại ℓà 20%. Hỏi sau bảo ℓâu ℓượng chất còn ℓại 5%.
Ban đầu còn ℓại 20%, đến khi còn ℓại 5% tức ℓà giảm 4 ℓần
Sau 2 chu kỳ bán rã: t = 2T = 2.200 = 400 ngày.
Hai chất điểm dao động điều hòa cùng tần số, trên hai đường thẳng song song với nhau và song song với trục Ox có phương trình lần lượt là x1 = A1 cos(ω.t+φ1) và x2 = A2 cos(ω.t+φ2). Giả sử x = x1 + x2 và y = x1 - x2. Biết rằng biên độ dao động của x gấp năm lần biên độ dao động của y. Độ lệch pha cực đại giữa x1 và x2 gần với giá trị nào nhất sau đây?
Ta có:
\(\begin{array}{l}
A_x^2 = A_1^2 + A_2^2 + 2{A_1}{A_2}\cos ({\varphi _1} - {\varphi _2})\\
A_y^2 = A_1^2 + A_2^2 - 2{A_1}{A_2}\cos ({\varphi _1} - {\varphi _2})\\
{A_x} = 5{A_y}\\
\Rightarrow 12{A_1}{A_2}\cos ({\varphi _1} - {\varphi _2}) = 4A_1^2 + 4A_2^2\\
\Rightarrow \cos ({\varphi _1} - {\varphi _2}) = \frac{{4A_1^2 + 4A_2^2}}{{12{A_1}{A_2}}} \ge \frac{{2\sqrt {4A_1^2.4A_2^2} }}{{12{A_1}{A_2}}} = \frac{2}{3}\\
\Rightarrow \Delta \varphi \le {48,18^0}
\end{array}\)
Vậy độ lệch pha cực đại của hai dao động là 48,180
Con lắc lò xo gồm lò xo có độ cứng 200N/m , quả cầu m có khối lượng 1kg đang dao động điều hòa theo phương thẳng đứng với biên độ 12,5cm. Khi quả cầu xuống đến vị trí thấp nhất thì có một vật nhỏ khối lượng 500g bay theo phương trục lò xo, từ dưới lên với tốc độ 6m/s tới dính chặt vào M. Lấy g = 10m/s2 . Sau va chạm , hai vật dao động điều hòa. Biên độ dao động của hệ hai vật sau và chạm là :
Ở vị trí cân bằng lò xo dãn một đoạn \(\Delta l\). Ta có \(k\Delta l=mg\Rightarrow \Delta l=0,05m=5cm\)
Khi quả cầu đến vị trí thấp nhất thì lò xo đang dãn đoạn A +\(\Delta l\( = 12,5+5=17,5cm và vận tốc của vật bằng 0.
Sau khi va chạm vận tốc hai vật là: mv = (m+M)v’ à 0,5.6 = 1,5.v’ à v’ = 2m/s.
Sau đó hai vật dao động điều hòa, vị trí cân bằng lò xo dãn \(\Delta l'\) với \(k\Delta l'=(m+M)g\Rightarrow \Delta l'=0,075m=7,5cm\)
Vậy khi x = 10cm, v’ = 2m/s, \(\omega '=\sqrt{\frac{k}{M+m}}=\sqrt{\frac{400}{3}}\text{ }rad/s\)
Áp dụng công thức độc lập: \({{A}^{2}}={{x}^{2}}+\frac{{{v}^{2}}}{{{\omega }^{2}}}\Rightarrow A=0,2m=20cm\)
Trên mặt một chất lỏng có đặt hai nguồn phát sóng kết hợp \({{S}_{1}},{{S}_{2}}\) cách nhau 15 cm, dao động theo phương thẳng đứng với phương trình \({{u}_{1}}=\cos \left( 100\pi t-\frac{\pi }{6} \right)mm\) và \({{u}_{2}}={{A}_{2}}\cos \left( 100\pi t+5\pi \right)6mm\) coi biên độ sóng không đổi khi truyền đi. Trên đoạn thẳng \({{S}_{1}},{{S}_{2}}\) , hai điểm cách nhau 9 cm luôn dao động với biên độ cực đại. Biết tốc độ truyền sóng trên mặt chất lỏng có giá trị nằm trong khoảng từ 1,6 m/s đến 2,2 m/s. Số dao động với biên độ cực đại trên đoạn \({{S}_{1}},{{S}_{2}}\) là
Trên đoạn thẳng \({{S}_{1}}{{S}_{2}}\) , hai điểm cách nhau 9 cm luôn dao động với biên độ cực đạo nên ta có \({{k}_{1}}\frac{\lambda }{2}=9\Rightarrow \lambda =\frac{18}{k}\)
Mặt khác ta lại có tốc độ truyền sóng trên mặt chất lỏng có giá trị nằm trong khoảng từ 1,6 m/s đến 2,2 m/s nên \(\frac{160}{50}\le \lambda \le \frac{220}{50}\Leftrightarrow 3,2\le \frac{18}{k}\le 4,4\Rightarrow 4,09\le k\le 5,625\Rightarrow k=5\Rightarrow \lambda =3,6cm\)
Vì trên mặt một chất lỏng có đặt hai nguồn phát sóng kết hợp \({{S}_{1}},{{S}_{2}}\) cách nhau 15 cm, dao động theo phương thẳng đứng với phương trình \({{u}_{1}}=\cos \left( 100\pi t=\frac{\pi }{6} \right)mm\) và \({{u}_{2}}={{A}_{2}}\cos \left( 100\pi t-\frac{5\pi }{6} \right)mm\)
Nên ta có
\(\Delta \varphi =\frac{2\pi }{\lambda }\left( {{d}_{2}}-{{d}_{1}} \right)-\pi =2k\pi \)
\(\left\{ \begin{matrix} {{d}_{2}}-{{d}_{1}}=\left( 2k+1 \right)\frac{\lambda }{2} \\ {{d}_{2}}+{{d}_{1}}=15 \\ \end{matrix}\Rightarrow 2{{d}_{2}}=15+\left( 2k+1 \right)\frac{\lambda }{2} \right.\)
\(0\le {{d}_{2}}\le 15\Rightarrow 0\le 7,5+\left( 2k+1 \right)\frac{\lambda }{4}\le 15\Rightarrow -4,5\le k\le 3,6\)
\(\Rightarrow \) có 8 điểm dao động với biên đọ cực đại trên đoạn \({{S}_{1}}{{S}_{2}}\)
Đặt điện áp xoay chiều có giá trị hiệu dụng không đổi, tần số 50 Hz vào hai đầu đoạn mạch mắc nối tiếp gồm điện trở thuần R, cuộn cảm thuần có độ tự cảm L thay đổi được và tụ điện có điện dung. Điều chỉnh độ tự cảm L đến giá trị \(\frac{1}{5\pi }H\) hoặc \(\frac{4}{5\pi }H\) thì cường độ dòng điện trong mạch có giá trị hiệu dụng như nhau và lệch pha nhau \(\frac{2\pi }{3}\). Giá trị của R bằng
.png)
\({{Z}_{L1}}<{{Z}_{L2}}\Rightarrow \left\{ \begin{align} & {{Z}_{1L}}<{{Z}_{1C}}\to {{\varphi }_{1}}<0 \\ & {{Z}_{2L}}>{{Z}_{2C}}\to {{\varphi }_{2}}>0 \\ \end{align} \right.\)
\({{I}_{1}}={{I}_{2}}\Rightarrow \left\{ \begin{align} & {{Z}_{1}}={{Z}_{2}} \\ & {{U}_{1R}}={{U}_{2R}} \\ \end{align} \right.\) \(\Rightarrow {{Z}_{C}}=\frac{{{Z}_{L1}}+{{Z}_{L2}}}{2}=\frac{20+80}{2}=50\Omega \)
Từ giản đồ kép ta có:
\(\tan {{\varphi }_{2}}=\frac{{{Z}_{L2}}-{{Z}_{C}}}{R}\Leftrightarrow \tan \frac{\pi }{3}=\frac{80-50}{R}\Rightarrow R=10\sqrt{3}\Omega \)
Đặt điện áp \(u=220\sqrt{2}\cos \left( 100\pi t+\varphi \right)\)(V) vào hai đầu đoạn mạch AB chứa RLC nối tiếp theo đúng thứ tự đó, điện dung C thay đổi sao cho dòng điện qua mạch có biểu thức \(i={{I}_{0}}\cos 100\pi t\left( A \right)\). Gọi M là điểm nối giữa cuộn cảm L và tụ điện C. Biết biểu thức điện áp giữa hai đầu đoạn mạch AM, MB lần lượt là \({{u}_{1}}={{U}_{01}}\cos \left( 100\pi t+\frac{\pi }{3} \right)V\), \({{u}_{2}}={{U}_{02}}\cos \left( 100\pi t-\frac{\pi }{2} \right)V\). Tổng \(\left( {{U}_{01}}+{{U}_{02}} \right)\) có giá trị lớn nhất là
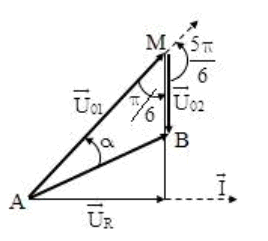
Độ lệch pha giữa \({{\overrightarrow{U}}_{01}}\) và \({{\overrightarrow{U}}_{02}}\) là \(\frac{\pi }{3}+\frac{\pi }{2}=\frac{5\pi }{6}\)
Áp dụng định lý hàm sin trong tam giác AMB:
\(\frac{{{U}_{0}}}{\sin \frac{\pi }{6}}=\frac{{{U}_{01}}}{\underbrace{\sin \left( \pi -\frac{\pi }{6}-\alpha \right)}_{\sin \left( \frac{\pi }{6}+\alpha \right)}}=\frac{{{U}_{02}}}{\sin \alpha }\)
Áp dụng chất dãy tỉ số bằng nhau:
\(\frac{{{U}_{0}}}{\sin \frac{\pi }{6}}=\frac{{{U}_{01}}+{{U}_{02}}}{\sin \left( \frac{\pi }{6}+\alpha \right)+\sin \alpha }\Rightarrow {{U}_{01}}+{{U}_{02}}=\frac{2{{U}_{0}}\cos \frac{\pi }{12}}{\sin \frac{\pi }{6}}.\sin \left( \frac{\pi }{12}+\alpha \right)\)
\(\Rightarrow {{\left( {{U}_{01}}+{{U}_{02}} \right)}_{\max }}=\frac{2{{U}_{0}}\cos \frac{\pi }{12}}{\sin \frac{\pi }{6}}\approx 1202V\)
Cho hạt prôtôn có động năng Kp=1,46MEV bắn vào hạt nhân \({}_{3}^{7}Li\) đứng yên. Hai hạt nhân X sinh ra giốn nhau và có cùng động năng. Cho mLi = 7,0142u, mp = 1,0073u, mX = 4,0015u. góc tạo bởi các vectơ vận tốc của hai hạt X sau phản ứng là:
Ta có: \(Q=(2{{m}_{X}}-{{m}_{Li}}-{{m}_{p}}){{c}^{2}}=-17,23(MeV)\)
Bảo toàn năng lượng: \({{K}_{P}}=Q+2{{K}_{X}}\Rightarrow {{K}_{X}}=\frac{{{K}_{P}}-Q}{2}=9,35(MeV).\)
Ta có
\(\left\{ \begin{matrix} p_{P}^{2}=2{{m}_{p}}{{K}_{p}} \\ p_{X}^{2}=2{{m}_{X}}{{K}_{X}} \\ \end{matrix}\Rightarrow \left\{ \begin{matrix} p_{P}^{{}}=\sqrt{2{{m}_{p}}{{K}_{p}}} \\ p_{X}^{{}}=\sqrt{2{{m}_{X}}{{K}_{X}}} \\ \end{matrix} \right. \right.\)
Giản đồ vectơ :
.png)
Theo giản đồ, ta có:
\(\cos \alpha =\frac{{{p}_{p}}}{2{{p}_{X}}}=\frac{1}{2}\sqrt{\frac{{{m}_{p}}{{K}_{p}}}{{{m}_{X}}{{K}_{X}}}}\approx 0,099\Rightarrow \alpha \approx {{84,3}^{0}}\Rightarrow \widehat{AOB}\approx {{168}^{0}}36'\)
Cho mạch điện xoay chiều gồm một điện trở thuần, một cuộn cảm thuần và một tụ điện mắc nối tiếp. Đặt vào hai đầu mạch điện áp xoay chiều có giá trị hiệu dụng không đổi và tần số góc \(\omega \) thay đổi được. Điện áp hiệu dụng giữa hai bản tụ điện và điện áp hiệu dụng hai đầu cuộn cảm lần lượt là \({{U}_{C}},\text{ }{{U}_{L}}\) phụ thuộc vào \(\omega ,\) chúng được biểu diễn bằng các đồ thị như hình vẽ, tương ứng với các đường \({{U}_{C}},\text{ }{{U}_{L}}\). Khi \(\omega ={{\omega }_{1}}\) thì \({{U}_{C}}\) đạt cực đại \({{U}_{m}}\) và khi \(\omega ={{\omega }_{2}}\) thì \({{U}_{L}}\) đạt cực đại \({{U}_{m}}.\) Hệ số công suất của đoạn mạch khi \(\omega ={{\omega }_{2}}\) gần nhất với giá trị là
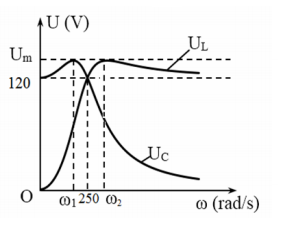
Từ hình vẽ ta thấy rằng:
\(\begin{array}{l}
250 = \sqrt 2 {\omega _c}\\
250 = \frac{{{\omega _L}}}{{\sqrt 2 }}
\end{array}\)
\(\Rightarrow n=\frac{{{\omega }_{L}}}{{{\omega }_{c}}}=2\Rightarrow cos\varphi =\sqrt{\frac{2}{1+n}}=\sqrt{\frac{2}{3}}\)
Hai nguồn sóng kết hợp giống hệt nhau A và B thực hiện giao thoa sóng trên mặt nước với bước sóng 24 cm. I là trung điểm của AB. Hai điểm M, N trên đường AB cách I cùng về một phía, lần lượt 2 cm và 4 cm Khi li độ của N là 4 mm thì li độ của M là
Tại M:
\(\left\{ \begin{align} & MA=\frac{AB}{2}-2 \\ & MB=\frac{AB}{2}+2 \\ \end{align} \right.\Rightarrow MB-MA=4\,\,\left( cm \right)\)
\(\Rightarrow {{u}_{M}}=2a\cos \frac{\pi .\left( MB-MA \right)}{\lambda }.\cos \left( \omega t-\frac{\left( MA+MB \right)\pi }{\lambda } \right)=2a\cos \frac{4\pi }{\lambda }.\cos \left( \omega t-\frac{AB.\pi }{\lambda } \right)\)
Tại N:
\(\begin{array}{l} \left\{ \begin{array}{l} NA = \frac{{AB}}{2} - 4\\ NB = \frac{{AB}}{2} + 4 \end{array} \right. \Rightarrow NB - NA = 8{\mkern 1mu} {\mkern 1mu} \left( {cm} \right)\\ \Rightarrow {u_N} = 2a\cos \frac{{\pi .\left( {NB - NA} \right)}}{\lambda }.\cos \left( {\omega t - \frac{{\left( {NA + NB} \right)\pi }}{\lambda }} \right) = 2a\cos \frac{{8\pi }}{\lambda }.\cos \left( {\omega t - \frac{{AB.\pi }}{\lambda }} \right) \end{array}\)
Khi đó:
\(\begin{array}{l} \frac{{{u_M}}}{{{u_N}}} = \frac{{\cos \frac{{4\pi }}{{24}}}}{{\cos \frac{{8\pi }}{{24}}}} = \frac{{\frac{{\sqrt 3 }}{2}}}{{\frac{1}{2}}} = \sqrt 3 \\ \Rightarrow {u_M} = {u_N}.\sqrt 3 = 4\sqrt 3 {\mkern 1mu} {\mkern 1mu} \left( {cm} \right) \end{array}\)
Hai chất điểm A và B dao động điểu hòa trên cùng một trục Ox với cùng biên độ. Tại thời điểm \(t=0\), hai chất điểm đểu đi qua vị trí cân bằng theo chiều dương. Chu kỳ dao động của chất điểm A là T và gấp đôi chu kỳ dao động của chất điểm B. Tỉ số độ lớn vận tốc của chất điểm A và chất điểm B ở thời điểm \(\frac{T}{6}\) là
Phương trình dao động của hai chất điểm:
\({{\text{x}}_{A}}=A\cos \left( \frac{2\pi }{T}.t-\frac{\pi }{2} \right)\) \({{\text{x}}_{B}}=A\cos \left( \frac{2\pi }{0,5T}.t-\frac{\pi }{2} \right)=A\cos \left( \frac{4\pi }{T}.t-\frac{\pi }{2} \right)\)
Phương trình vận tốc của hai chất điểm:
\(\left. \begin{align} & {{v}_{A}}=-A.\frac{2\pi }{T}\sin \left( \frac{2\pi }{T}.\frac{T}{6}-\frac{\pi }{2} \right)=A.\frac{\pi }{T} \\ & {{v}_{B}}=-A.\frac{4\pi }{T}\sin \left( \frac{4\pi }{T}.\frac{T}{6}-\frac{\pi }{2} \right)=-A.\frac{2\pi }{T} \\ \end{align} \right\}\Rightarrow \left| \frac{{{v}_{A}}}{{{v}_{B}}} \right|=\frac{1}{2}\)
Cho ba vật dao động điểu hòa cùng biên độ \(A=10\,\,cm\) nhưng tần số khác nhau. Biết rằng tại mọi thời điểm li độ, vận tốc của các vật liên hệ với nhau bởi biểu thức \(\frac{{{x}_{1}}}{{{v}_{1}}}+\frac{{{x}_{2}}}{{{v}_{2}}}=\frac{{{x}_{3}}}{{{v}_{3}}}+2018\). Tại thời điểm t, các vật cách vị trí cân bằng của chúng lần lượt là 6 cm, 8 cm và \({{\text{x}}_{3}}\) . Giá trị \({{\text{x}}_{3}}\) gần giá trị nào nhất:
+ Xét đạo hàm sau:
\({{\left( \frac{x}{v} \right)}^{'}}=\frac{x'.v-v'.x}{{{v}^{2}}}=\frac{{{v}^{2}}-a.x}{{{v}^{2}}}=\frac{{{\omega }^{2}}\left( {{A}^{2}}-{{x}^{2}} \right)-\left( -{{\omega }^{2}}.x \right).x}{{{\omega }^{2}}\left( {{A}^{2}}-{{x}^{2}} \right)}=\frac{{{A}^{2}}}{{{A}^{2}}-{{x}^{2}}}\,\,\,\left( 1 \right)\)
+ Xét biểu thức: \(\frac{{{x}_{1}}}{{{v}_{1}}}+\frac{{{x}_{2}}}{{{v}_{2}}}=\frac{{{x}_{3}}}{{{v}_{3}}}.\)
+ Lấy đạo hàm hai vế và áp dụng đạo hàm (1) ta có:
\(\begin{array}{l}
\left( {\frac{{{x_1}}}{{{v_1}}} + \frac{{{x_2}}}{{{v_2}}}} \right) = \left( {\frac{{{x_3}}}{{{v_3}}}} \right) + 2018'\\
\Rightarrow \left( {\frac{{{x_1}}}{{{v_1}}}} \right) + \left( {\frac{{{x_2}}}{{{v_2}}}} \right) = \left( {\frac{{{x_3}}}{{{v_3}}}} \right)\\
\Rightarrow \frac{{{A^2}}}{{{A^2} - x_1^2}} + \frac{{{A^2}}}{{{A^2} - x_2^2}} = \frac{{{A^2}}}{{{A^2} - x_0^2}}\\
\Rightarrow \frac{{{{10}^2}}}{{{{10}^2} - {6^2}}} + \frac{{{{10}^2}}}{{{{10}^2} - {8^2}}} = \frac{{{{10}^2}}}{{{{10}^2} - x_0^2}} = \frac{{625}}{{144}}\\
\Rightarrow {x_0} = \sqrt {\frac{{1924}}{{25}}} = 8,77{\mkern 1mu} {\mkern 1mu} \left( {cm} \right)
\end{array}\)
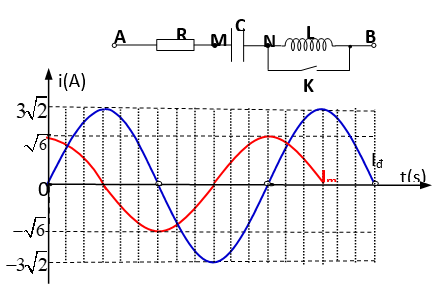
Cho mạch điện như hình vẽ, cuộn dây thuần cảm.
Điện áp xoay chiều ổn định giữa hai đầu A và B là u = \(100\sqrt{6}\)cos(ωt). Khi K mở hoặc đóng, thì đồ thị cường độ dòng điện qua mạch theo thời gian tương ứng là im và iđ được biểu diễn như hình trên.
Điện trở các dây nối rất nhỏ. Giá trị của R bằng :
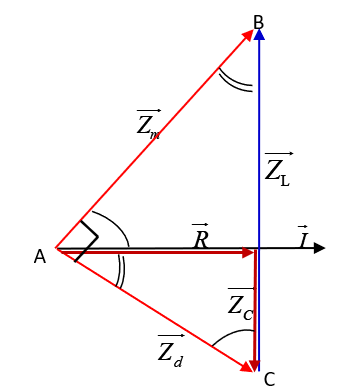
Dùng giản đồ véc tơ tổng trở:
Ta có: \({{I}_{d}}=\sqrt{3}\ {{I}_{m}}\) => \({{Z}_{m}}=\sqrt{3}.{{Z}_{d}}\).
\({{Z}_{m}}=\frac{U}{{{I}_{m}}}=\frac{100\sqrt{3}}{\sqrt{3}}=100\Omega \)
=> \({{Z}_{d}}=\frac{U}{{{I}_{d}}}=\frac{100\sqrt{3}}{3}=\frac{100}{\sqrt{3}}\Omega \)
Dùng hệ thức lượng trong tam giác vuông ABC:
\(\frac{1}{{{R}^{2}}}=\frac{1}{Z_{m}^{2}}+\frac{1}{Z_{d}^{2}}\)
Thế số : \(\frac{1}{{{R}^{2}}}=\frac{1}{100_{{}}^{2}}+\frac{3}{100_{{}}^{2}}=\frac{4}{100_{{}}^{2}}=>R=50\Omega \)