2p\(\frac{x}{\lambda }\) = \(\pi \)x → \(\pi \) = 2 m → v = \(\pi \).\(\frac{\omega }{2\pi }\) = 2.\(\frac{6\pi }{2\pi }\) = 6 (m/s).

Đáp án C.

L’ = lg\(\frac{I'}{I{}_{0}}\) = lg\(\frac{10I}{{{I}_{0}}}\) = lg10 + lg\(\frac{I}{{{I}_{0}}}\) = 1 B + L.

Đáp án C.

U₂ = \(\frac{{{N}_{2}}}{{{N}_{1}}}\)U₁ = 11 V.

Đáp án D.

w = \(\frac{2\pi }{T}\) = 5p rad/s = \(\sqrt{\frac{g}{\Delta {{l}_{0}}}}\) 

Dl₀ = \(\frac{g}{{{\omega }^{2}}}\) = 0,04 m = 4 cm;  

l₀ = l – Dl₀ = 40 cm.

Đáp án B.

d = (5 – 1)\(\frac{\lambda }{2}\) = 2,5\(\lambda \).    

Đáp án C.

I = \(\frac{U}{2\pi fL}\); I’ = \(\frac{U}{2\pi f'L}\)

→ \(\frac{I'}{I}=\frac{f}{f'}\)

→ I’ = I\(\frac{f}{f'}\) = 2,5 A.

Đáp án A.

Điện áp giữa hai bản tụ trể pha \(\frac{\pi }{2}\) so với cường độ dòng điện nên u và i cùng pha (j = 0) → P = P_max = \(\frac{{{U}^{2}}}{R}\) = 400 W.

Đáp án C.

T = 2p\(\sqrt{\frac{l}{g}}\) = 1,1 s

v = \(\frac{L}{T}\)=11,36 m/s = 40,9 km/h.

Đáp án A.

w = \(\frac{2\pi }{T}\)= p rad/s; khi t = 0 thì x = 0 → cosj = cos(±\(\frac{\pi }{2}\)); khi t = 0 thì v > 0 → j = - \(\frac{\pi }{2}\).

Đáp án D.

\(\lambda \) = \(\frac{v}{f}\) = 1,5 cm. - \(\frac{{{S}_{1}}{{S}_{2}}}{\lambda }\)= - 6,7 < k < \(\frac{{{S}_{1}}{{S}_{2}}}{\lambda }\) = 6,7

→ có 13 cực đại. Cực đại gần S₂ nhất ứng với k = 6 nên d₁ – d₂ = 6\(\lambda \)

→ d₂ = d₁ - 6\(\lambda \) = S₁S₂ - 6\(\lambda \) = 1 cm = 10 mm.

Đáp án C.

\(\Delta \)l₀ = A = \(\frac{F}{k}\) = 0,05 m = 5 cm. T = 2π\(\sqrt{\frac{m}{k}}\) = \(\frac{\pi }{10}\) s.

Thời điểm t = \(\frac{\pi }{3}\) = 3\(\frac{\pi }{10}\) + \(\frac{\pi }{30}\) = 3T + \(\frac{T}{3}\) có: x = \(\frac{A}{2}\) và v = v_max\(\frac{\sqrt{3}}{2}\) = wA\(\frac{\sqrt{3}}{2}\).

So với vị trí cân bằng khi không còn lực F tác dụng (vị trí lò xo không biến dạng) thì x’ = A + \(\frac{A}{2}\) = \(\frac{3A}{2}\) và v’ = v = wA\(\frac{\sqrt{3}}{2}\).

Con lắc dao động với biên độ: A’ = \(\sqrt{{{(x')}^{2}}+{{\left( \frac{v'}{\omega } \right)}^{2}}}\)= A\(\sqrt{3}\) = 8,66 cm.

Đáp án A.

Quan sát hình vẽ, ta thấy trong thời gian 0,3 s sóng truyền được quãng đường bằng \(\frac{3}{8}\)l tức là: 0,3 s = \(\frac{3}{8}\)T

→ T = 0,8 s. Tại thời điểm t₂ N đang đi qua vị trí cân bằng theo chiều dương (N đi lên) nên:

v =  v_max = wA = \(\frac{2\pi }{T}\)A = 39,3cm/s.

Đáp án D.

Khi có cộng hưởng điện I = I_max = I_m = \(\frac{U}{R}\);

\(\omega \)\(_{0}^{2}\) =  \(\frac{1}{LC}\) → C = \(\frac{1}{\omega _{0}^{2}L}\) = \(\frac{5\pi }{4\omega _{0}^{2}}\)

Khi \(\omega \)₁ = \(\omega \)₂ thì I₀₁ = I₀₂ = I_m = \(\frac{{{I}_{0m}}}{\sqrt{2}}\)= \(\frac{{{U}_{0}}}{R\sqrt{2}}\) → \(\omega \)\(_{0}^{2}\) = \(\omega \)₁\(\omega \)₂ 

và Z = \(\sqrt{{{R}^{2}}+{{({{Z}_{L}}-{{Z}_{C}})}^{2}}}\)

R = Z_L – Z_C = \(\omega \)₁L - \(\frac{1}{{{\omega }_{1}}C}\) = \(\frac{4}{5\pi }\)\(\omega \)₁ - \(\frac{1}{{{\omega }_{1}}.\frac{5\pi }{4{{\omega }_{1}}{{\omega }_{2}}}}\)  = \(\frac{4}{5\pi }\)(\(\omega \)₁ –  \(\omega \)₂) = 160 W.

Đáp án C.

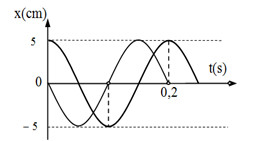
T=0,2s; \(x={{x}_{1}}+{{x}_{2}}=5c\text{os}\left( \text{10}\pi \text{t+}\frac{\pi }{\text{2}} \right)+5c\text{os10}\pi \text{t=5}\sqrt{\text{2}}c\text{os}\left( \text{10}\pi \text{t+}\frac{\pi }{\text{4}} \right)cm\)

Một chu kỳ vật chuyển động được quãng đường 4A=20\(\sqrt{2}\)cm;=> \(t=4T+\frac{T}{8}\)

Tần số dao động của con lắc có chu kì T=1(s) là: \(f=\frac{1}{T}=\frac{1}{1}=1\left( Hz \right)$, $f=\frac{1}{2\pi }\sqrt{\frac{k}{m}}\)

Tần số dao động mới của con lắc xác định từ phương trình

\({{f}^{'}}=\frac{1}{2\pi }\sqrt{\frac{k}{{{m}^{'}}}}\)

\(\Rightarrow \frac{f}{{{f}^{'}}}=\sqrt{\frac{k}{m}}.\sqrt{\frac{{{m}^{'}}}{k}}=\sqrt{\frac{{{m}^{'}}}{m}}\)  

\(\Rightarrow \frac{1}{0,5}=\sqrt{\frac{{{m}^{'}}}{m}}\Leftrightarrow {{m}^{'}}=4m\)

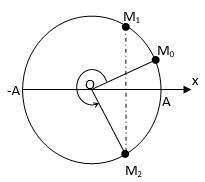
Ta có \(\left\{ \begin{array}{l} x = 2\\ v > 0 \end{array} \right. \Rightarrow \left\{ \begin{array}{l} x = 4c{\rm{os}}(4\pi t + \frac{\pi }{6}) = 2\\ v = - 16\pi \sin (4\pi t + \frac{\pi }{6}) > 0 \end{array} \right. \Rightarrow 4\pi t + \frac{\pi }{6} = - \frac{\pi }{3} + k2\pi \)

→ \(t=-\frac{1}{8}+\frac{k}{2}\text{  k}\in {{\text{N}}^{*}}\)   

Thời điểm thứ 3 ứng với k = 3 → \(t=\frac{11}{8}s\)

Chọn A.

L₂ – L₁=30dB suy ra 10\(10\lg \frac{{{I}_{2}}}{{{I}_{0}}}-10\lg \frac{{{I}_{1}}}{{{I}_{0}}}=30\,\Rightarrow \,\lg \frac{{{I}_{2}}}{{{I}_{1}}}=3\Rightarrow \frac{{{I}_{2}}}{{{I}_{1}}}={{10}^{3}}\)

Chọn A.         

Vì nam châm có dòng điện xoay chiều chạy qua lên nó sẽ tác dụng lên dây một lực tuần hoàn làm dây dao động cưỡng bức.Trong một T(s) dòng điện đổi chiều 2 lần nên nó hút dây 2 lần . Vì vậy tần số dao động của dây = 2 lần tần số của dòng điện.

Tần số sóng trên dây là:   f’ = 2.f =2.50 =100Hz

Vì trên dây có sóng dừng với 2 bó sóng nên: AB = L =2. \(\frac{\lambda }{2}\to \lambda =L=60cm\)

→  v = \(\lambda .f=60.100=6000cm/s=60m/s\)

Chọn A

-Cảm kháng : \({{Z}_{L}}=L.\omega =\frac{3}{\pi }100\pi =300\Omega \);   

Dung kháng : \({{Z}_{C}}=\frac{1}{\omega .C}=\frac{1}{100\pi .\frac{{{10}^{-4}}}{2\pi }}\) = 200 \(\Omega \)

-Tổng trở : Z = \(\sqrt{{{R}^{2}}+{{({{Z}_{L}}-{{Z}_{C}})}^{2}}}=\sqrt{{{100}^{2}}+{{(300-200)}^{2}}}=100\sqrt{2}\Omega \)

- Điện áp cực đại : U₀ = I₀.Z = 2.\(100\sqrt{2}\)V =200\(\sqrt{2}\)V

-Độ lệch pha : \(tg\phi =\frac{{{Z}_{L}}-{{Z}_{C}}}{R}=\frac{300-200}{100}=1\Rightarrow \phi ={{45}^{0}}=\frac{\pi }{4}rad\)

-Pha ban đầu của điện áp: \({{\phi }_{u}}={{\phi }_{i}}+\phi =0+\frac{\pi }{4}=\) \(\frac{\pi }{4}rad\)

-Biểu thức điện áp : u = \({{U}_{0}}\cos (\omega t+{{\phi }_{u}})=200\sqrt{2}\cos (100\pi t+\frac{\pi }{4})\) V

Ta có pha của điện áp hai đầu mạch nhanh hơn điện áp hai đầu tụ \(\frac{\pi }{2}\) ; nghĩa là cùng pha CĐDĐ;

 vì điện áp hai đầu tụ chậm hơn CĐDĐ \(\frac{\pi }{2}\)=> xảy ra hiện tượng cộng hưởng. Khi đó  Z_L = Z_C              

\(\Leftrightarrow {{Z}_{L}}=\frac{1}{\omega .C}\Rightarrow C=\frac{1}{\omega .{{Z}_{L}}}=\frac{1}{100\pi .100}=\frac{{{10}^{-4}}}{\pi }\) F

Chọn A

Dùng \(P=U.I.c\text{os}\varphi \) .Với  j =ju -ji  =  - p/6- (-p/2) = p/3 ; I= 4A; U =100V

Chọn A

\(\text{W}=\frac{q_{0}^{2}}{2C}\) = Wt + Wd  (1)  mà đề cho: Wt =3Wd  (2)  với  \({{\text{W}}_{d}}=\frac{q_{{}}^{2}}{2C}\)

Thế (2) vào (1) :  W = 4Wd  → \(\frac{q_{0}^{2}}{2C}=4\frac{{{q}^{2}}}{2C}\) => \(q=\pm \frac{q_{0}^{{}}}{2}\)

Chọn C:

\(\lambda =\frac{a.i}{D}=\frac{0,{{3.10}^{-3}}{{.3.10}^{-3}}}{1,5}=0,{{6.10}^{-6}}m=0,6\mu m\)

Chọn D: \(i=\frac{\lambda D}{a}=\frac{0,{{6.10}^{-6}}.2,5}{{{10}^{-3}}}=1,{{5.10}^{-3}}m=1,5mm\)

Số vân trên một nửa trường giao thoa: \(\frac{L}{2i}=\frac{12,5}{2.1,5}=4,16\)

→ số vân tối quan sát được trên màn là: N_t = 2.4 = 8 vân tối.

Và số vân sáng quan sát được trên màn là:  N_s = 2.4+1 = 9 vân sáng.

Vậy tổng số vân quan sát được là 8 + 9 =17 vân.

Chọn B:

Vị trí các vân sáng: \({{x}_{s}}=k\frac{\lambda .D}{a}\to \lambda =\frac{{{x}_{s}}.a}{k.D}=\frac{3,3}{k}\)

Với ánh sáng trắng:  0,4 \( \le \lambda  \le \) 0,75 → \(0,4\le \frac{3,3}{k}\le 0,75\to 4,4\le k\le 8,25\) 

Chọn k=5, 6, 7, 8: Có bốn bức xạ cho vân sáng tại đó.

Chọn B: 

Wđ = V_Max.e = \(hc(\frac{1}{\lambda }-\frac{1}{{{\lambda }_{0}}})\)

Số nguyên tử còn lại ≈ 1,69.10­¹⁷

Đáp án B

Trong máy quang phổ lăng kính, lăng kính có tác dụng tán sắc ánh sáng

Đáp án B

Tia hồng ngoại được ứng dụng để sưởi ấm

Đáp án C

Câu C sai do năng lượng của các phôtôn của các ánh sáng đơn sắc khác nhau là khác nhau chứ không phải bằng nhau

Đáp án D

Sự lan truyền sóng cơ là sự truyền các dao động trong môi trường chân không không có phần tử dao động nên sóng cơ không lan truyền được

Đáp án C

Dải sóng điện từ trên có tần số nằm trong khoảng 2.10¹³ Hz đến 8.10¹³ Hz có bước sóng nằm trong khoảng 1,5.10^-5m đến 3,75.10^-6m thuộc vùng tia hồng ngoại

Đáp án B

Tia X bị chặn bởi lớp chì dày vài milimet nên câu B sai

Đáp án D

Bước sóng của sóng điện từ truyền trong chân không được xác định bởi biểu thức  \(\lambda =\frac{c}{f}\)

Đáp án A

Pin quang điện hoạt động dựa trên hiện tượng quang điện trong

Đáp án B

Cảm kháng của cuộn dây được xác định bởi biểu thức:

\({{Z}_{L}}=\omega L=100\pi .\frac{0,2}{\pi }=20\Omega \)

Đáp án A

Giới hạn quang điện của đồng được xác định bởi biểu thức:

\(\lambda =\frac{hc}{A}=\frac{6,{{625.10}^{-34}}{{.3.10}^{8}}}{6,{{625.10}^{-19}}}={{3.10}^{-7}}m=0,3\mu m\)

Đáp án A

Hiện tượng cộng hưởng xảy ra khi tần số của ngoại lực cưỡng bức bằng tần số riêng của hệ

Đáp án B

Vận tốc góc: ω = 100 rad/s

Khi vòng dây quay 1000 vòng thì góc quay được: ∆α = 1000.2π = 2000π (rad/s)

=> Thời gian quay hết 1000 vòng là: \(t=\frac{\Delta \alpha }{\omega }=\frac{2000\pi }{100}=20\pi \left( s \right)\)

=> Nhiệt lượng toả ra trên vòng dây khi nó quay được 1000 vòng là:

\(Q=\frac{{{U}^{2}}}{R}t=\frac{{{\left( \frac{\omega BS}{\sqrt{2}} \right)}^{2}}}{R}t={{\frac{\left( \omega BS \right)}{2R}}^{2}}.t=\frac{{{\left( 100.0,{{1.100.10}^{-4}} \right)}^{2}}}{2.0,314}.20\pi =1J\)

Bước sóng: λ = vT = v/f = 12cm

Biên độ của điểm M và N:

\(\left\{ \begin{align} & {{A}_{M}}=2a.\left| c\text{os}\frac{\pi \left( MB-AM \right)}{\lambda } \right| \\ & {{A}_{N}}=2a.\left| c\text{os}\frac{\pi \left( BN-AN \right)}{\lambda } \right| \\ \end{align} \right.\Rightarrow \frac{{{A}_{M}}}{{{A}_{N}}}=\frac{\left| c\text{os}\frac{\pi \left( MB-AM \right)}{\lambda } \right|}{\left| c\text{os}\frac{\pi \left( BN-AN \right)}{\lambda } \right|}=\frac{\left| c\text{os}\frac{\pi \left( 17-15 \right)}{12} \right|}{\left| c\text{os}\frac{\pi \left( 14,5-10,5 \right)}{12} \right|}\)

\(\Rightarrow \frac{12}{{{A}_{N}}}=\frac{c\text{os}30}{c\text{os}60}=\sqrt{3}\Rightarrow {{A}_{N}}=4\sqrt{3}cm\)