Đề thi thử THPT QG năm 2022 môn Vật Lý - Trường THPT Nguyễn Duy Hiệu
Đề thi thử THPT QG năm 2022 môn Vật Lý
-
Hocon247
-
40 câu hỏi
-
90 phút
-
42 lượt thi
-
Dễ
Tham gia [ Hs Hocon247.com ] - Cộng Đồng Luyện Thi Trực Tuyến để được học tập những kiến thức bổ ích từ HocOn247.com
Điện năng truyền tải đi xa thường bị tiêu hao, chủ yếu do tỏa nhiệt trên đường dây. Gọi R là điện trở đường dây, P là công suất được truyền đi, U là điện áp tại nơi phát, cosφ là hệ số công suất của mạch điện thì công suất tỏa nhiệt trên đường dây là
Công suất tỏa nhiệt trên đường dây là: \(\Delta P=\frac{{{P}^{2}}}{{{(U\cos \varphi )}^{2}}}R\)
Chọn A.
Một dây dẫn thẳng dài đặt trong không khí có dòng điện với cường độ I chạy qua. Độ lớn cảm ứng từ B do dòng điện này gây ra tại một điểm cách dây một đoạn r được tính bởi công thức
Độ lớn cảm ứng từ do dòng điện gây ra là: \(B={{2.10}^{-7}}\frac{I}{r}\)
Chọn D.
Cho đoạn mạch điện xoay chiều gồm 2 trong 3 phần tử R, L, C mắc nối tiếp. Điện áp giữa hai đầu đoạn mạch và cường độ dòng điện trong mạch có biểu thức: \(u={{U}_{0}}\cos \left( 100\pi t-\frac{\pi }{6} \right)\) và \(i={{I}_{0}}\cos \left( 100\pi t+\frac{\pi }{4} \right)\). Mạch điện gồm
Độ lệch pha giữa điện áp và cường độ dòng điện là:
\(\varphi ={{\varphi }_{u}}-{{\varphi }_{i}}=-\frac{\pi }{6}-\frac{\pi }{4}=-\frac{5\pi }{12}\text{ (rad)}\)
→ điện áp trễ pha hơn cường độ dòng điện
→ mạch điện chứa hai phần tử R và C
Chọn C.
Một con lắc lò xo nằm ngang, người ta kích thích cho con lắc dao động điều hòa với biên độ 5 cm thì chu kì dao động là 1,0 s. Nếu kích thích cho con lắc dao động điều hòa với biên độ 10 cm thì chu kì dao động là
Chu kì của con lắc lò xo phụ thuộc vào khối lượng vật nặng và độ cứng của lò xo, không phụ thuộc vào biên độ dao động
→ Chu kì dao động của con lắc là: \(\text{T}=1\text{s}\)
Chọn D.
Để có hiện tượng sóng dừng trên dây một sợi dây đàn hồi có một đầu cố định, một đầu tự do, thì chiều dài l của sợi dây phải thỏa mãn điều kiện
Điều kiện xảy ra sóng dừng trên dây một đầu cố định, một đầu tự do: \(l=(2k+1)\frac{\lambda }{4}(k\in N)\)
Chọn C.
Chọn câu sai. Tổng hợp hai dao động điều hòa cùng phương, cùng tần số, cùng biên độ A là một dao động điều hòa cùng phương, cùng tần số với hai dao động thành phần và có biên độ là
Biên độ dao động tổng hợp là: \(A=\sqrt{A_{1}^{2}+A_{2}^{2}+2{{A}_{1}}{{A}_{2}}\cos \Delta \varphi }\)
Với \(\Delta \varphi =\frac{\pi }{2}\Rightarrow A=A\sqrt{2}\to A\)đúng
Với \(\Delta \varphi =0\Rightarrow A=2A\to B\)đúng
Với \(\Delta \varphi =\frac{2\pi }{3}\Rightarrow A=A\to C\)đúng
Với \(\Delta \varphi =\frac{\pi }{3}\Rightarrow A=A\sqrt{3}\to D\)sai
Chọn D.
Đặt điện áp xoay chiều \(u={{U}_{0}}\cos \omega t\) vào hai đầu đoạn mạch chỉ có điện trở thuần. Gọi I0 là cường độ dòng điện cực đại, U và I là điện áp và cường độ dòng điện hiệu dụng, u và i là giá trị tức thời. Hệ thức nào sau đây sai?
Đoạn mạch chứa điện trở thuần → điện áp cùng pha với cường độ dòng điện
Hệ thức không đúng là: \(\frac{{{u}^{2}}}{U_{0}^{2}}+\frac{{{i}^{2}}}{I_{0}^{2}}=1\)
Chọn B.
Một cây cầu bắc ngang qua sông Phô-tan-ka ở thành phố Xanh Pê-téc-bua (Nga) được thiết kế xây dựng đủ vững chắc, có thể cho cùng lúc 300 người đi qua mà cầu không sập. Năm 1906 có một trung đội bộ binh gồm 36 người đi đều bước qua cây cầu làm cho cây cầu gãy. Sự cố gãy cầu là do
Sự cố gãy cầu là do xảy ra hiện tượng cộng hưởng cơ ở cầu
Chọn B.
Một vật dao động điều hòa theo phương trình \(x=A\cos (\omega t+\varphi )\) với \(A>0,\omega >0.\). Biên độ của dao động là
Phương trình dao động: \(x=A\cos (\omega t+\varphi )\)có biên độ dao động là A
Chọn D.
Để phân loại sóng ngang, sóng dọc, người ta dựa vào
Để phân biệt sóng ngang, sóng dọc, người ta dựa vào phương dao động và phương truyền sóng
Chọn C.
Trong bài hát “Tiếng đàn bầu” của nhạc sỹ Nguyễn Đình Phúc có đoạn: Tiếng đàn bầu của ta cung thanh là tiếng mẹ, cung trầm là giọng cha, ngân nga con vẫn hát, tích tịch tình tang. “Thanh” và “trầm” ở đây nói đến đặc trưng nào của âm?
“Thanh”, “trầm” chỉ đặc trưng độ cao của âm
Chọn B.
Giá trị hiệu dụng của điện áp xoay chiều \(u=200\sqrt{3}\cos (120\pi t)\text{ V}\) là
Điện áp hiệu dụng của dòng điện xoay chiều là:
\(U=\frac{{{U}_{0}}}{\sqrt{2}}=\frac{200\sqrt{3}}{\sqrt{2}}=100\sqrt{6}(V)\)
Chọn D.
Một chất điểm dao động điều hòa theo phương trình vận tốc \(v=20\pi \cos \left( 2\pi t+\frac{3\pi }{4} \right)cm.{{s}^{-1}}.\) Lúc vật chuyển động
Phương trình vận tốc của chất điểm là:
\(v=20\pi \cos \left( 2\pi t+\frac{3\pi }{4} \right)(cm/s)\Rightarrow a=40{{\pi }^{2}}\cos \left( 2\pi t+\frac{5\pi }{4} \right)(cm)\)
Ở thời điểm t = 0,5 s, ta có: \(\left\{ \begin{array}{*{35}{l}} a=20{{\pi }^{2}}\sqrt{2}(cm)>0 \\ v=10\pi \sqrt{2}(cm/s)>0 \\ \end{array} \right.\)
→ Vật chuyển động nhanh dần theo chiều dương
Chọn A.
Con lắc lò xo gồm vật nặng khối lượng m = 100 g và lò xo nhẹ có độ cứng k = 100 N/m. Tác dụng một ngoại lực cưỡng bức biến thiên điều hòa với biên độ F0 và tần số f1 = 6 Hz thì biên độ dao động ổn định là A1. Nếu giữ nguyên biên độ F0 mà tăng tần số ngoại lực đến f2 = 10 Hz thì biên độ dao động ổn định là A2. So sánh A1 và A2
Tần số của con lắc lò xo là: \({{f}_{0}}=\frac{1}{2\pi }\sqrt{\frac{k}{m}}=\frac{1}{2\pi }\sqrt{\frac{100}{0,1}}\approx 5,0\text{3 (Hz)}\)
Nhận xét: tần số f1 gần với tần số dao động riêng f0 của con lắc hơn tần số f2
→ Biên độ A1 > A2
Chọn C.
Để xác định điện động E của một nguồn điện, một học sinh mắc mạch điện như hình bên (H1). Đóng khóa K và điều chỉnh con chạy C, kết quả đo được mô tả bởi đồ thị biểu diễn sự phụ thuộc của \(\frac{1}{I}\) (nghịch đảo số chỉ của ampe kế A) vào giá trị R của biến trở như hình bên (H2). Giá trị trung bình của E được xác định bởi thí nghiệm này là
.jpg)
Từ đồ thị ta thấy có 2 cặp giá trị \(\left( \frac{1}{I};R \right)\) là \((60;40)\) và \((100;80)\)
Ta có công thức định luật Ôm:
\(I=\frac{E}{R+{{R}_{0}}+r}\Rightarrow \frac{1}{I}=\frac{R+{{R}_{0}}+r}{E}\)
Thay các cặp giá trị vào công thức, ta có:
\(\left\{ \begin{array}{*{35}{l}} 60=\frac{40+\left( {{R}_{0}}+r \right)}{E} \\ 100=\frac{80+\left( {{R}_{0}}+r \right)}{E} \\ \end{array}\Rightarrow \left\{ \begin{array}{*{35}{l}} {{R}_{0}}+r=20(\Omega ) \\ E=1(V) \\ \end{array} \right. \right.\)
Chọn C.
Vật sáng AB có dạng đoạn thẳng nhỏ đặt vuông góc với trục chính (A nằm trên trục chính) của thấu kính phân kỳ. Khi tịnh tiến AB dọc theo trục chính ra xa thấu kính thì ảnh A’B’ của AB cho bởi thấu kính
Vật dịch chuyển ra xa thấu kính → ảnh dịch chuyển ra xa thấu kính và dịch chuyển lại gần tiêu điểm ảnh của thấu kính
Độ phóng đại của ảnh là: \(k=\frac{f}{f-d}\)
Vật dịch chuyển ra xa thấu kính → d tăng → k giảm → độ cao của vật nhỏ dần
Chọn B.
Một sóng cơ truyền trên mặt nước với tần số 5 Hz. Tại thời điểm t vị trí các phần tử mặt nước có dạng như hình vẽ. Trong đó khoảng cách từ vị trí cân bằng của A đến vị trí cân bằng của Q là 15 cm và điểm P đang từ vị trí cân bằng của nó đi lên. Sóng này truyền từ
.jpg)
Ta có hình vẽ biểu diễn mối liên hệ giữa chiều truyền sóng và chiều dao động của phần tử môi trường:
Điểm P đang có xu hướng đi xuống → sóng truyền từ phải qua trái (truyền từ B đến A)
Từ hình vẽ ta thấy khoảng cách giữa hai điểm A, Q là:
\(AQ=\frac{3\lambda }{4}=15(cm)\Rightarrow \lambda =20(cm)\)
Vận tốc truyền sóng là: v = λf = 20.5 = 100 (cm/s) = 1 (m/s)
Chọn B.
Một bóng đèn sợi tóc có ghi 220 V – 100 W được mắc vào mạng điện xoay chiều có điện áp hiệu dụng 220 V. Điện năng tiêu thụ của đèn trong 1 giờ là
Điện năng tiêu thụ của đèn trong 1h là:
A = P.t = 100.3600 = 360000 (J) = 100 (Wh)
Chọn A.
Thí nghiệm giao thoa sóng trên mặt chất lỏng với hai nguồn kết hợp cùng pha. Biết bước sóng bằng 20 cm. Nếu điểm M nằm trên đường cực tiểu giao thoa thì hiệu đường đi từ hai nguồn đến điểm M có thể là giá trị
Điểm M là cực tiêu giao thoa có:
\({{d}_{2}}-{{d}_{1}}=\left( k+\frac{1}{2} \right)\lambda =\left( k+\frac{1}{2} \right).20=20k+10(cm)\) với \(\text{k}=0;\pm 1;\pm 2\ldots \)
Với k = 2 → d = 50 cm
Chọn A.
Chọn câu đúng. Đưa quả cầu tích điện Q lại gần quả cầu M nhỏ, nhẹ, bằng bấc, treo ở đầu một sợi chỉ thẳng đứng. Quả cầu bấc M bị hút dính vào quả cầu Q. Sau đó thì
Quả cầu M bị hút dính vào quả cầu Q → sau đó hai quả cầu có điện tích cùng dấu
→ Quả cầu M bị đẩy lệch về phía xa Q
Chọn A.
Một đèn điện mắc vào điện áp xoay chiều \(200\sqrt{2}\cos 100\pi t\text{ (V)}\text{.}\) Đèn chỉ sáng khi điện áp tức thời hai đầu đèn có độ lớn \(\left| u \right|\ge 100\sqrt{2}V.\) Số lần đèn tắt trong 1 s là
Nhận xét: trong 1 chu kì, đèn tắt 2 lần
Chu kì của dòng điện là: \(T=\frac{2\pi }{\omega }=\frac{2\pi }{100\pi }=0,02(s)\)
Trong 1 s, số chu kì của dòng điện là: \(n=\frac{t}{T}=\frac{1}{0,02}=50\)
Số lần đèn tắt trong 1 s là: \(N=2n=100\) (lần)
Chọn B.
Tại một phòng thí nghiệm, học sinh A sử dụng con lắc đơn để đo gia tốc rơi tự do g bằng phép đo gián tiếp. Kết quả đo chu kì và chiều dài của con lắc đơn là T = 1,919 ± 0,001 (s) và l = 0,900 ± 0,002 (m). Bỏ qua sai số của số π. Cách viết kết quả đo nào sau đây là đúng?
Chu kì của con lắc đơn là:
\(T=2\pi \sqrt{\frac{l}{g}}\Rightarrow g=\frac{4{{\pi }^{2}}l}{{{T}^{2}}}\Rightarrow \bar{g}=\frac{4{{\pi }^{2}}\bar{l}}{{{{\bar{T}}}^{2}}}=\frac{4.{{\pi }^{2}}.0,9}{1,{{919}^{2}}}=9,648\left( \text{m/}{{\text{s}}^{\text{2}}} \right)\)
Sai số của phép đo là:
\(\frac{\Delta g}{{\bar{g}}}=\frac{\Delta l}{{\bar{l}}}+2\frac{\Delta T}{{\bar{T}}}\Rightarrow \frac{\Delta g}{9,648}=\frac{0,002}{0,9}+2\cdot \frac{0,001}{1,919}\Rightarrow \Delta g=0,031\left( \text{m/}{{\text{s}}^{\text{2}}} \right)\)
\(\Rightarrow g=9,648\pm 0,031\left( \text{m/}{{\text{s}}^{\text{2}}} \right)\)
Chọn D.
Phương trình sóng tại nguồn O có dạng \({{u}_{O}}=A\cos \left( \omega t-\frac{\pi }{2} \right)cm.\) Sóng truyền dọc theo phương Ox với biên độ A và bước sóng λ không đổi. Điểm M trên phương Ox, cách O một đoạn \(OM=\frac{\lambda }{6}\) vào thời điểm \(t=\frac{\pi }{2\omega }\) có li độ bằng \(\sqrt{3}\text{cm}.\) . Biên độ A có giá trị bằng
Phương trình sóng tại điểm M là:
\({{u}_{M}}=A\cos \left( \omega t-\frac{\pi }{2}-\frac{2\pi d}{\lambda } \right)=A\cos \left( \omega t-\frac{\pi }{2}-\frac{\pi }{3} \right)\)
Tại thời điểm t, điểm M có li độ là:
\({{u}_{M}}=A\cos \left( 2\pi -\frac{\pi }{2}-\frac{\pi }{3} \right)=\sqrt{3}\Rightarrow A=2(cm)\)
Chọn C.
Ở cùng một nơi trên Trái Đất, các con lắc đơn dao động điều hòa. Con lắc đơn có chiều dài l1 dao động điều hòa với chu kì T1, con lắc đơn có chiều dài l2 dao động điều hòa với chu kì T2. Con lắc đơn có chiều dài \(2{{l}_{1}}+3{{l}_{2}}\) dao động điều hòa với chu kì
Chu kì của con lắc đơn là: \(T=2\pi \sqrt{\frac{l}{g}}\Rightarrow l=\frac{g{{T}^{2}}}{4{{\pi }^{2}}}\Rightarrow l\sim {{T}^{2}}\)
→ Chu kì của con lắc đơn có chiều dài \(2{{l}_{1}}+3{{l}_{2}}\) là: \(\sqrt{4T_{1}^{2}+9T_{2}^{2}}\)
Chọn D.
Đặt điện áp xoay chiều \(u=200\cos \left( 100\pi t+\frac{\pi }{4} \right)V\)vào hai đầu đoạn mạch gồm cuộn dây thuần cảm có độ tự cảm L thay đổi được, điện trở R và tụ điện có điện dung C mắc nối tiếp theo thứ tự. Điều chỉnh L thì thấy điện áp hiệu dụng giữa hai đầu cuộn cảm đạt cực đại bằng \(200\sqrt{2}V.\) Khi đó biểu thức điện áp giữa hai đầu tụ điện là
Khi L thay đổi để \({{\text{U}}_{\text{Lmax}}},\) ta có:
\({{U}_{C}}{{U}_{L\max }}=U_{L\max }^{2}-{{U}^{2}}\) \(\Rightarrow {{U}_{C}}=\frac{U_{L\max }^{2}-{{U}^{2}}}{{{U}_{L\max }}}=\frac{{{\left( 200\sqrt{2} \right)}^{2}}-{{\left( 100\sqrt{2} \right)}^{2}}}{200\sqrt{2}}=\frac{300}{\sqrt{2}}(V)\)
\(\Rightarrow {{U}_{0C}}={{U}_{C}}\sqrt{2}=300(V)\)
Lại có: \(\overrightarrow{U}\bot \overrightarrow{{{U}_{RC}}}\Rightarrow {{\varphi }_{RC}}={{\varphi }_{u}}-\frac{\pi }{2}=-\frac{\pi }{4}(rad)\)
Mà \({{\varphi }_{C}}<{{\varphi }_{RC}}\Rightarrow {{\varphi }_{C}}<-\frac{\pi }{4}\Rightarrow {{\varphi }_{C}}=-\frac{5\pi }{12}(rad)\)
\(\Rightarrow {{u}_{C}}=300\cos \left( 100\pi t-\frac{5\pi }{12} \right)(V)\)
Chọn C.
Ở mặt chất lỏng, tại hai điểm A và B có hai nguồn kết hợp, dao động cùng pha theo phương thẳng đứng. Gọi M là điểm thuộc mặt chất lỏng, nằm trên đường thẳng Ax vuông góc với Biết phần tử chất lỏng tại M dao động với biên độ cực đại, giữa M và đường trung trực của AB có 3 cực tiểu giao thoa. Số cực tiểu giao thoa trên đoạn thẳng MB là
Nhận xét: giữa M và đường trung trực của AB có 3 cực tiểu giao thoa
→ Tại M là cực đại bậc 3 (k = 3)
Ta có hình vẽ:
.jpg)
Tại điểm M có:
\(MB-MA=3\lambda \Rightarrow \sqrt{2A{{B}^{2}}}-AB=3\lambda \Rightarrow AB=\frac{3\lambda }{\sqrt{2}-1}=7,24\lambda \)
Số cực tiểu trên đoạn IB là: \(n=\left( \frac{AB}{\lambda } \right)=7\)
Số cực tiểu trên đoạn IM là: 3
Số cực tiểu trên đoạn MB là: 3 + 7 = 10
Chọn A.
Đặt điện áp \(u=200\sqrt{2}\cos (100\pi t)\) (u tính bằng V, t tính bằng s) vào hai đầu đoạn mạch AB gồm điện trở thuần \(R=50\Omega \) mắc nối tiếp với đoạn mạch X. Cường độ dòng điện hiệu dụng qua đoạn mạch là \(\sqrt{3}A.\) Biết ở thời điểm t, điện áp tức thời giữa hai đầu AB có giá trị \(200\sqrt{2}V;\) ở thời điểm \(t+\frac{1}{300}s,\) cường độ dòng điện tức thời qua đoạn mạch bằng không và đang giảm. Công suất tiêu thụ điện của đoạn mạch X là
Ban đầu điện áp có giá trị \(\text{u}={{\text{U}}_{0}}\)
Khoảng thời gian \(\frac{1}{300}s\) tương ứng với góc quét là:
\(\Delta \varphi =\omega \Delta t=100\pi .\frac{1}{300}=\frac{\pi }{3}(rad)\)
Cường độ dòng điện qua mạch bằng 0 và đang giảm, ta có vòng tròn lượng giác:
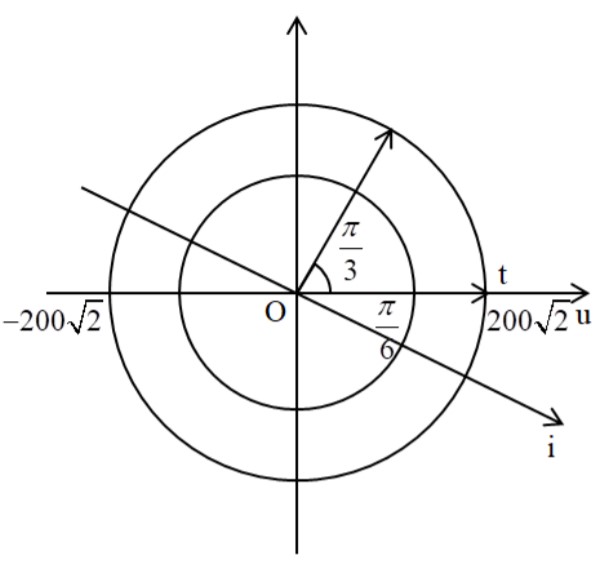
Từ vòng tròn lượng giác, ta thấy cường độ dòng điện sớm pha hơn điện áp góc: \(\varphi =\frac{\pi }{6}(rad)\)
Công suất tiêu thụ trên đoạn mạch X là:
\({{P}_{X}}=P-{{P}_{R}}=UI\cos \varphi -{{I}^{2}}R\) \(\Rightarrow {{P}_{X}}=200.\sqrt{3}.\cos \frac{\pi }{6}-{{\left( \sqrt{3} \right)}^{2}}.50=150(W)\)
Chọn C.
Cho một vật có khối lượng m = 200 g tham gia đồng thời hai dao động điều hòa cùng phương, cùng tần số với phương trình lần lượt là \({{x}_{1}}=\sqrt{3}\sin \left( 20t+\frac{\pi }{2} \right)cm\) và \({{x}_{2}}=2\cos \left( 20\pi t+\frac{5\pi }{6} \right)cm.\)
Độ lớn của hợp lực tác dụng lên vật tại thời điểm \(t=\frac{\pi }{120}s\) là
Ta có phương trình dao động: \({{x}_{1}}=\sqrt{3}\sin \left( 20t+\frac{\pi }{2} \right)=\sqrt{3}\cos (20t)\)
Sử dụng máy tính bỏ túi, ta có:
\(\sqrt{3}\angle 0+2\angle \frac{5\pi }{6}=1\angle \frac{\pi }{2}\Rightarrow \left\{ \begin{array}{*{35}{l}} A=1(cm) \\ \varphi =\frac{\pi }{2}(rad) \\ \end{array} \right.\) \(\Rightarrow x=1\cos \left( 20t+\frac{\pi }{2} \right)(cm)\)
Tại thời điểm \(\frac{\pi }{120}s,\) li độ của vật là
\(x=\cos \left( 20\cdot \frac{\pi }{120}+\frac{\pi }{2} \right)=-0,5(cm)=-0,005(m)\)
Hợp lực tác dụng lên vật có độ lớn là:
\(F=\left| -m{{\omega }^{2}}x \right|=\left| -0,{{2.20}^{2}}.0,005 \right|=0,4(N)\)
Chọn A.
Một hòn đá được thả rơi tự do xuống một giếng cạn nước hình trụ có đường kính 120 cm. Một người dùng đồng hồ bấm giây, ghé sát tai vào miệng giếng, sau 3 s kể từ lúc thả thì người đó nghe thấy tiếng hòn đá đập vào đáy giếng. Giả sử tốc độ truyền âm trong không khí là 330 m/s. Lấy \(\text{g}=9,8\text{m/}{{\text{s}}^{\text{2}}}.\) Thể tích của giếng có giá trị gần đúng là
Thời gian kể từ lúc thả hòn đá đến khi nghe thấy tiếng hòn đá đập vào đáy giếng là: \(t=\sqrt{\frac{2h}{g}}+\frac{h}{v}\Rightarrow \sqrt{\frac{2h}{9,8}}+\frac{h}{330}=3\Rightarrow h\approx 40,4(m)\)
Thể tích của giếng là: \(V=S.h=\pi \frac{{{d}^{2}}}{4}.h=\pi .\frac{1,{{2}^{2}}}{4}.40,4=45,69\left( {{m}^{3}} \right)\)
Thể tích của giếng gần nhất với giá trị 45,87 m3
Chọn B.
Một con lắc đơn có chiều dài 2 m được treo tại một điểm cách mặt sàn nằm ngang 12 m. Con lắc đơn dao động điều hòa với biên độ góc \({{\alpha }_{0}}=0,1\) rad, tại nơi có gia tốc trọng trường g = 9,8 m/s2. Khi vật đang đi qua vị trí thấp nhất thì dây bị đứt. Khoảng cách từ hình chiếu của điểm treo con lắc lên mặt sàn đến điểm mà vật rơi trên sàn là
Tại vị trí thấp nhất, con lắc đi qua vị trí cân bằng (α = 0), tốc độ của vật nặng là:
\(v=\sqrt{2gl\left( \cos \alpha -\cos {{\alpha }_{0}} \right)}=\sqrt{2gl\left( 1-\cos {{\alpha }_{0}} \right)}\)
Độ cao của vật khi dây bị đứt là: \(h=12-2=10(m)\)
Khi dây bị đứt, vật chuyển động như chuyển động ném ngang với vận tốc đầu \({{\text{v}}_{0}}=\text{v}\)
Tầm xa của vật đạt được là:
\(L=v\sqrt{\frac{2h}{g}}=\sqrt{2gl\left( 1-\cos {{\alpha }_{0}} \right)}.\sqrt{\frac{2h}{g}}=2\sqrt{lh\left( 1-\cos {{\alpha }_{0}} \right)}\)
\(\Rightarrow L=2\sqrt{2.10.\left( 1-\cos 5,{{7}^{0}} \right)}\approx 0,632(m)=20\sqrt{10}(cm)\)
Chọn D.
Đặt vào hai đầu cuộn sơ cấp của một máy biến áp lí tưởng (bỏ qua hao phí) một điện áp xoay chiều có giá trị hiệu dụng không đổi thì điện áp hiệu dụng giữa hai đầu cuộn thứ cấp để hở là 100 V. Ở cuộn thứ cấp, nếu giảm bớt n vòng dây thì điện áp hiệu dụng giữa hai đầu để hở của nó là U, nếu tăng thêm n vòng dây thì điện áp đó là 2U. Nếu tăng thêm 3n vòng dây ở cuộn thứ cấp thì điện áp hiệu dụng giữa hai đầu để hở của cuộn này bằng
Áp dụng công thức máy biến áp, ban đầu ta có:
\(\frac{{{N}_{1}}}{{{N}_{2}}}=\frac{{{U}_{1}}}{{{U}_{2}}}=\frac{{{U}_{1}}}{100}\text{ (1)}\)
Thay đổi số vòng dây ở cuộn thứ cấp, ta có:
\(\left\{ \begin{array}{*{35}{l}} \frac{{{N}_{1}}}{{{N}_{2}}-n}=\frac{{{U}_{1}}}{U} \\ \frac{{{N}_{1}}}{{{N}_{2}}+n}=\frac{{{U}_{1}}}{2U} \\ \end{array}\Rightarrow \frac{{{N}_{2}}-n}{{{N}_{2}}+n}=\frac{U}{2U}=\frac{1}{2}\Rightarrow {{N}_{2}}=3n \right.\)
Tăng thêm 3n vòng dây ở cuộn thứ cấp, ta có:
\(\frac{{{N}_{1}}}{{{N}_{2}}+3n}=\frac{{{U}_{1}}}{{{U}_{2}}'}\Rightarrow \frac{{{N}_{2}}}{2{{N}_{2}}}=\frac{{{U}_{1}}}{{{U}_{2}}'}\text{ (2)}\)
Từ (1) và (2) ta có: \(2=\frac{{{U}_{2}}'}{100}\Rightarrow {{U}_{2}}'=200(V)\)
Chọn D.
Một khung dây phẳng quay đều quanh một trục cố định thuộc mặt phẳng của nó, trong một từ trường đều có vectơ cảm ứng từ vuông góc với trục quay. Tại thời điểm t1, từ thông gửi qua khung dây và suất điện động cảm ứng xuất hiện trong khung dây có độ lớn bằng 0,25 Wb và \(5\sqrt{3}V.\) Đến thời điểm t2, từ thông gửi qua khung dây và suất điện động cảm ứng xuất hiện trong khung dây có độ lớn bằng \(0,25\sqrt{3}Wb\) và 5 V. Khi suất điện động cảm ứng xuất hiện trong khung dây có độ lớn bằng giá trị hiệu dụng thì từ thông gửi qua khung dây có độ lớn bằng
Nhận xét: từ thông và suất điện động biến đổi vuông pha
Áp dụng công thức độc lập với thời gian cho hai thời điểm t1 và t2, ta có:
\(\left\{ \begin{array}{*{35}{l}} \frac{{{\left( 5\sqrt{3} \right)}^{2}}}{E_{0}^{2}}+\frac{0,{{25}^{2}}}{\Phi _{0}^{2}}=1 \\ \frac{{{5}^{2}}}{E_{0}^{2}}+\frac{{{\left( 0,25\sqrt{3} \right)}^{2}}}{\Phi _{0}^{2}}=1 \\ \end{array}\Rightarrow \left\{ \begin{array}{*{35}{l}} {{E}_{0}}=10(V) \\ {{\Phi }_{0}}=0,5(Wb) \\ \end{array} \right. \right.\)
Suất điện động có độ lớn bằng giá trị hiệu dụng, ta có:
\(\frac{{{E}^{2}}}{E_{0}^{2}}+\frac{{{\Phi }^{2}}}{\Phi _{0}^{2}}=1\Rightarrow \frac{{{\left( 5\sqrt{2} \right)}^{2}}}{{{10}^{2}}}+\frac{{{\Phi }^{2}}}{0,{{5}^{2}}}=1\Rightarrow \Phi =0,25\sqrt{2}(Wb)\)
Chọn C.
Một chất điểm có khối lượng m = 300 g thực hiện đồng thời hai dao động điều hòa cùng phương, cùng tần số, cùng biên độ, có li độ phụ thuộc thời gian như hình vẽ. Nếu \({{t}_{2}}-{{t}_{1}}=\frac{1}{6}s\) thì cơ năng của chất điểm gần giá trị nào nhất sau đây?
.jpg)
Nhận xét: hai dao động có cùng biên độ A
Từ đồ thị ta thấy trong khoảng thời gian từ t1 đến t2, dao động 1 dịch chuyển từ li độ 4 cm về vị trí cân bằng, dao động 2 dịch chuyển từ li độ 4 cm, đến biên dương và về li độ 4 cm
Ta có vòng tròn lượng giác:
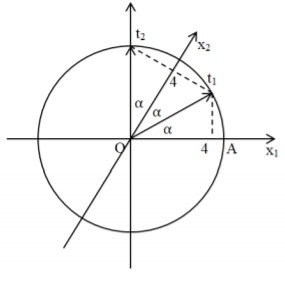
Từ vòng tròn lượng giác ta thấy: \(\alpha ={{30}^{0}}=\frac{\pi }{6}(rad)\)
Khoảng thời gian từ t1 đến t2 là:
\(\Delta t={{t}_{2}}-{{t}_{1}}=\frac{1}{6}\Rightarrow \omega =\frac{\Delta \varphi }{\Delta t}=\frac{2\alpha }{\Delta t}=\frac{\frac{\pi }{3}}{\frac{1}{6}}=2\pi (ra\text{d/s)}\)
Lại có \(ar\cos \frac{4}{A}={{30}^{0}}\Rightarrow \frac{4}{A}=\cos {{30}^{0}}=\frac{\sqrt{3}}{2}\Rightarrow A=\frac{8}{\sqrt{3}}(cm)\)
Độ lệch pha giữa hai dao động là: \(\varphi =2\alpha =\frac{\pi }{3}(rad)\)
Biên độ dao động tổng hợp là:
\({{A}_{0}}=\sqrt{A_{1}^{2}+A_{2}^{2}+2{{A}_{1}}{{A}_{2}}\cos \frac{\pi }{3}}=A\sqrt{3}=8(cm)\)
Cơ năng của vật là:
\(W=\frac{1}{2}m{{\omega }^{2}}A_{0}^{2}=\frac{1}{2}.0,3.{{(2\pi )}^{2}}.0,{{08}^{2}}\approx 0,0379(J)=37,9(mJ)\)
Chọn C.
Có hai con lắc lò xo giống hệt nhau, dao động điều hòa trên mặt phẳng nằm ngang dọc theo hai đường thẳng song song cạnh nhau và song song với trục Ox. Biên độ của con lắc thứ nhất là \({{\text{A}}_{1}}=4\text{cm},\) của con lắc thứ hai là \({{A}_{2}}=4\sqrt{3}cm,\) con lắc thứ hai dao động sớm pha hơn con lắc thứ nhất. Trong quá trình dao động, khoảng cách lớn nhất giữa hai vật là a = 4 cm. Khi động năng của con lắc thứ nhất đạt cực đại là W thì động năng của con lắc thứ hai là
Khoảng cách lớn nhất giữa hai chất điểm là:
\({{d}_{\max }}=\sqrt{A_{1}^{2}+A_{2}^{2}-2{{A}_{1}}{{A}_{2}}\cos \varphi }\) \(\Rightarrow 4=\sqrt{{{4}^{2}}+{{\left( 4\sqrt{3} \right)}^{2}}-2.4.4\sqrt{3}.\cos \varphi }\)
\(\Rightarrow \cos \varphi =\frac{\sqrt{3}}{2}\Rightarrow \varphi ={{\varphi }_{2}}-{{\varphi }_{1}}=\frac{\pi }{6}(rad)\)
Động năng cực đại của con lắc thứ nhất là:
\({{W}_{d1\max }}=W=\frac{1}{2}m{{\omega }^{2}}A_{1}^{2}\text{ (1)}\)
Con lắc thứ nhất có động năng cực đại, giả sử khi đó pha dao động là \({{\varphi }_{1}}=\frac{\pi }{2}\)
\(\Rightarrow {{\varphi }_{2}}=\frac{\pi }{6}+\frac{\pi }{2}=\frac{2\pi }{3}(rad)\Rightarrow {{x}_{2}}={{A}_{2}}\cos {{\varphi }_{2}}=4\sqrt{3}.\cos \frac{2\pi }{3}=-2\sqrt{3}(cm)\)
Động năng của con lắc thứ hai khi đó là:
\({{W}_{d2}}=\frac{1}{2}m{{\omega }^{2}}\left( A_{2}^{2}-x_{2}^{2} \right)\text{ (2)}\)
Từ (1) và (2) ta có:
\(\frac{{{W}_{d2}}}{W}=\frac{A_{2}^{2}-x_{2}^{2}}{A_{1}^{2}}=\frac{{{\left( 4\sqrt{3} \right)}^{2}}-{{\left( 2\sqrt{3} \right)}^{2}}}{{{4}^{2}}}=\frac{9}{4}\Rightarrow {{W}_{d2}}=\frac{9W}{4}\)
Chọn A.
Trên một sợi dây đàn hồi OC đang có sóng dừng ổn định với bước sóng λ, chu kỳ T. Hình ảnh sợi dây tại thời điểm t (nét đứt) và thời điểm \(t+\frac{T}{4}\)(nét liền) được cho như hình vẽ. Biết quãng đường mà điểm B trên dây đi được trong một chu kì T là \(x=\frac{\lambda }{2}.\) Bước sóng λ có giá trị là
.jpg)
Xét điểm D có tọa độ như hình vẽ
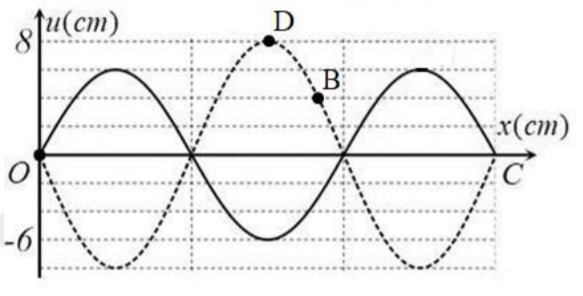
Nhận xét: tại thời điểm t, chất điểm D có li độ u = 8 cm, ở thời điểm \(t+\frac{T}{4},\) chất điểm có li độ u = -6 cm
Hai thời điểm có độ lệch pha là: \(\Delta \varphi =\omega \Delta t=\frac{2\pi }{T}\cdot \frac{T}{4}=\frac{\pi }{2}(rad)\)
Ta có vòng tròn lượng giác:
.jpg)
Từ đồ thị ta thấy: \(ar\cos \frac{8}{{{A}_{D}}}+ar\cos \frac{6}{{{A}_{D}}}={{90}^{0}}\Rightarrow {{A}_{D}}=10(cm)\)
Điểm B và D thuộc cùng bó sóng → chúng dao động cùng pha
Tại thời điểm t, li độ của hai điểm B và D là:
\(\frac{{{u}_{B}}}{{{u}_{D}}}=\frac{{{A}_{B}}}{{{A}_{D}}}\Rightarrow \frac{4}{8}=\frac{{{A}_{B}}}{10}\Rightarrow {{A}_{B}}=5(cm)\)
Quãng đường chất điểm B đi được trong 1 chu kì là:
\(S=4A\Rightarrow \frac{\lambda }{2}=4{{A}_{B}}\Rightarrow \lambda =8{{A}_{B}}=40(cm)\)
Chọn B.
Hai thanh ray xA và yB đặt song song, cách nhau 20 cm trên mặt phẳng ngang. Lò xo có độ cứng k = 15 N/m liên kết với một thanh dẫn MN có khối lượng m = 200 g, có thể chuyển động tịnh tiến, không ma sát, luôn vuông góc và tiếp xúc với hai thanh ray. Hệ thống được đặt trong từ trường đều có phương vuông góc với mặt phẳng hình vẽ, có độ lớn B = 50 T. Tụ điện có điện dung C = 250 µF. Bỏ qua điện trở của hai thanh ray. Kích thích cho thanh MN dao động điều hòa với chu kỳ T. Giá trị của T gần giá trị nào nhất sau đây?
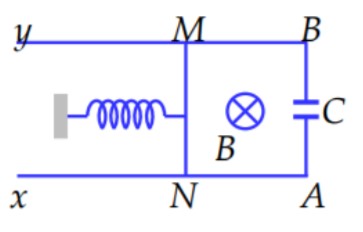
Thanh dẫn MN chuyển động, suất điện động tự cảm trong thanh là: \({{\text{e}}_{\text{c}}}=\text{B}l\text{v}\)
Điện tích của tụ điện là: \(\text{q}=\text{C}.{{\text{e}}_{\text{c}}}=\text{C}.\text{Blv}\)
Cường độ dòng điện chạy qua thanh MN là: \(\text{i}=\text{{q}'}=(\text{CBlv}{)}'=\text{CBla}\)
Lực từ tác dụng lên thanh MN là: \({{\text{F}}_{\text{t}}}=\text{iBl}=\text{C}{{\text{B}}^{2}}{{l}^{2}}\text{a}\)
Áp dụng định luật II Niu-tơn, ta có:
\({{F}_{dh}}+{{F}_{t}}=ma\Rightarrow -kx+C{{B}^{2}}{{l}^{2}}a=ma\)
\(\Rightarrow ~a.~\left( m-C{{B}^{2}}{{l}^{2}} \right)+kx=0\Rightarrow {x}''+\frac{k}{m-C{{B}^{2}}{{l}^{2}}}x=0\)
→ Thanh MN dao động điều hòa với tần số góc \(\omega =\sqrt{\frac{k}{m-C{{B}^{2}}{{l}^{2}}}}\)
Chu kì dao động của thanh là:
\(T=\frac{2\pi }{\omega }=2\pi \sqrt{\frac{m-C{{B}^{2}}{{l}^{2}}}{k}}=2\pi \sqrt{\frac{0,2-{{250.10}^{-6}}{{.50}^{2}}.0,{{2}^{2}}}{15}}\approx 0,679(s)\)
Chu kì T gần nhất với giá trị 0,657 s
Chọn A.
Trong thí nghiệm giao thoa sóng với hai nguồn kết hợp A, B trên mặt nước, dao động cùng pha. Xét hai điểm C, D thuộc đường thẳng Ay vuông góc với AB tại A, với CA = 9 cm, DA = 16 cm. Dịch chuyển nguồn B dọc theo đường thẳng chứa AB đến khi góc CBD là lớn nhất thì thấy C và D thuộc hai cực đại giao thoa liền kề. Gọi M là điểm nằm trên Ay dao động với biên độ cực tiểu. Giá trị lớn nhất của AM là
Ta có hình vẽ:
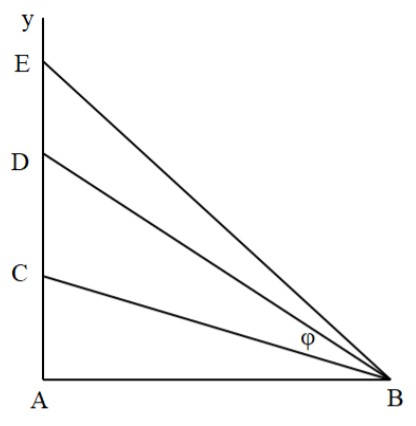
Để \(CB{{D}_{\max }}\Rightarrow {{\alpha }_{\max }}\Rightarrow {{(\tan \alpha )}_{\max }}\)
Xét \(\tan \alpha =\tan (ABD-ABC)=\frac{\tan ABD-\tan ABC}{1+\tan ABD\tan ABC}\)
\(\Rightarrow \tan \alpha =\frac{\frac{AD}{AB}-\frac{AC}{AB}}{1+\frac{AD}{AB}\cdot \frac{AC}{AB}}=\frac{AD-AC}{AB+\frac{AD.AC}{AB}}=\frac{7}{AB+\frac{144}{AB}}\)
Để \({{(\tan \alpha )}_{\max }}\Rightarrow {{\left( AB+\frac{144}{AB} \right)}_{\min }}\)
Áp dụng bất đẳng thức Cô – si, ta có:
\(AB+\frac{144}{AB}\ge 2\sqrt{AB\cdot \frac{144}{AB}}\Rightarrow {{\left( AB+\frac{144}{AB} \right)}_{\min }}\Leftrightarrow AB=12(cm)\)
AB AB AB Tại C, D là hai cực đại liên tiếp
→ D là cực đại bậc k, C là cực đại bậc (k+1), ta có:
\(\left\{ \begin{array}{*{35}{l}} DB-DA=\sqrt{D{{A}^{2}}+A{{B}^{2}}}-DA=k\lambda \Rightarrow k\lambda =4 \\ CB-CA=\sqrt{C{{A}^{2}}+A{{B}^{2}}}-CA=(k+1)\lambda \Rightarrow (k+1)\lambda =6 \\ \end{array}\Rightarrow \lambda =2(cm) \right.\)
Xét điểm E là cực tiểu xa A nhất → E là cực tiểu bậc 1 (k = 0)
Ta có:
\(EB-EA=\frac{1}{2}\lambda \Rightarrow \sqrt{E{{A}^{2}}+A{{B}^{2}}}-EA=\frac{1}{2}\lambda \)
\(\Rightarrow \sqrt{E{{A}^{2}}+{{12}^{2}}}-EA=1\Rightarrow EA=71,5(cm)\)
Chọn D.
Đặt điện áp \(u={{U}_{0}}\cos (100\pi t)\text{ V}\) vào hai đầu mạch điện nối tiếp như hình bên. Đoạn mạch gồm điện trở R, cuộn dây thuần cảm có độ tự cảm L, tụ điện có điện dung C thay đổi được. Khi \(\text{C}={{\text{C}}_{1}}\) và \(\text{C}={{\text{C}}_{2}}=0,5{{\text{C}}_{1}}\) thì điện áp tức thời \({{\text{u}}_{\text{AN}}}\) có cùng giá trị hiệu dụng nhưng lệch pha nhau 600. Cho biết \(R=50\sqrt{3}\Omega ,\) điện dung C1 có giá trị là
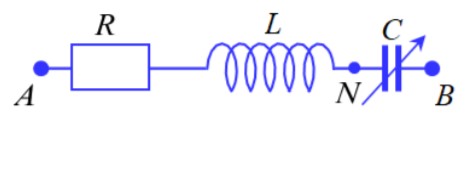
Ta có: \({{Z}_{C2}}=0,5{{Z}_{C1}}=\frac{1}{2}{{Z}_{C1}}\Rightarrow {{Z}_{C2}}=2{{Z}_{C1}}\)
Điện áp hiệu dụng giữa hai đầu đoạn mạch AN là: \({{u}_{AN}}=\frac{U\sqrt{{{R}^{2}}+Z_{L}^{2}}}{\sqrt{{{R}^{2}}+{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}}}\)
Khi C = C1 và C = C2, điện áp hiệu dụng giữa hai đầu đoạn mạch AN có cùng giá trị, ta có:
\(\frac{U\sqrt{{{R}^{2}}+Z_{L}^{2}}}{\sqrt{{{R}^{2}}+{{\left( {{Z}_{L}}-{{Z}_{C1}} \right)}^{2}}}}=\frac{U\sqrt{{{R}^{2}}+Z_{L}^{2}}}{\sqrt{{{R}^{2}}+{{\left( {{Z}_{L}}-{{Z}_{C2}} \right)}^{2}}}}\) \(\Rightarrow {{\left( {{Z}_{L}}-{{Z}_{C1}} \right)}^{2}}={{\left( {{Z}_{L}}-{{Z}_{C2}} \right)}^{2}}\)
\(\Rightarrow \left( \begin{array}{*{35}{l}} {{Z}_{L}}-{{Z}_{C1}}={{Z}_{L}}-{{Z}_{C2}}\text{ (loai)} \\ {{Z}_{L}}-{{Z}_{C1}}=-\left( {{Z}_{L}}-{{Z}_{C2}} \right) \\ \end{array} \right.\) \(\Rightarrow {{Z}_{L}}=\frac{{{Z}_{C1}}+{{Z}_{C2}}}{2}=\frac{3}{2}{{Z}_{C1}}\)
Độ lệch pha giữa điện áp hai đầu đoạn mạch AN và cường độ dòng điện là:
\(\tan {{\varphi }_{AN}}=\frac{{{Z}_{L}}}{R}=~const~\Rightarrow {{\varphi }_{AN/i}}=~const~\)
Độ lệch pha giữa điện áp hai đầu đoạn mạch AN trong các trường hợp là:
\(\Delta \varphi ={{\varphi }_{1{{u}_{AN}}}}-{{\varphi }_{2{{u}_{AN}}}}={{\varphi }_{i1}}-{{\varphi }_{i2}}=\frac{\pi }{3}(rad)\)
Ta có: \(\tan \frac{\pi }{3}=\tan \left( {{\varphi }_{i1}}-{{\varphi }_{i2}} \right)=\frac{\tan {{\varphi }_{i1}}-\tan {{\varphi }_{i2}}}{1+\tan {{\varphi }_{i1}}\tan {{\varphi }_{i2}}}\)
\(\Rightarrow \frac{\frac{{{Z}_{L}}-{{Z}_{C1}}}{R}-\frac{{{Z}_{L}}-{{Z}_{C2}}}{R}}{1+\frac{{{Z}_{L}}-{{Z}_{C1}}}{R}\cdot \frac{{{Z}_{L}}-{{Z}_{C2}}}{R}}=\frac{2R\left( {{Z}_{L}}-{{Z}_{C1}} \right)}{{{R}^{2}}-{{\left( {{Z}_{L}}-{{Z}_{C1}} \right)}^{2}}}=\sqrt{3}\)
\(\Rightarrow 2R\left( {{Z}_{L}}-{{Z}_{C1}} \right)=\sqrt{3}{{R}^{2}}-\sqrt{3}{{\left( {{Z}_{L}}-{{Z}_{C1}} \right)}^{2}}\Rightarrow {{Z}_{L}}-{{Z}_{C1}}=\frac{R}{\sqrt{3}}=50(\Omega )\)
\(\Rightarrow \frac{3}{2}{{Z}_{C1}}-{{Z}_{C1}}=50\Rightarrow {{Z}_{C1}}=100(\Omega )\)
Dung kháng của tụ điện là:
\({{Z}_{C1}}=\frac{1}{\omega {{C}_{1}}}\Rightarrow {{C}_{1}}=\frac{1}{\omega {{Z}_{C1}}}=\frac{1}{100.100\pi }=\frac{{{10}^{-4}}}{\pi }(F)\)
Chọn A.
Đặt điện áp xoay chiều có giá trị hiệu dụng U không đổi vào hai đầu đoạn mạch AB mắc nối tiếp gồm cuộn dây thuần cảm có độ tự cảm L, điện trở R và tụ điện có điện dung C. Tần số góc ω của điện áp là thay đổi được. Hình vẽ bên là đồ thị biểu diễn sự phụ thuộc của điện áp hiệu dụng trên L theo giá trị tần số góc ω. Lần lượt cho ω bằng x, y và z thì mạch AB tiêu thụ công suất lần lượt là P1, P2 và P3. Biểu thức nào sau đây đúng?
.jpg)
Điện áp hiệu dụng giữa hai đầu cuộn dây là:
\({{U}_{L}}=\frac{U.{{Z}_{L}}}{\sqrt{{{R}^{2}}+{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}}}=\frac{U.{{Z}_{L}}}{R}\cdot \frac{R}{\sqrt{{{R}^{2}}+{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}}}=\frac{U.{{Z}_{L}}.\cos \varphi }{R}\)
Với tần số \({{\omega }_{1}}=x;{{\omega }_{2}}=y\) và \({{\omega }_{3}}=z,\) ta có: \(\frac{1}{\omega _{1}^{2}}+\frac{1}{\omega _{3}^{2}}=\frac{2}{\omega _{2}^{2}}\)
Từ đồ thị ta thấy:
\({{U}_{L1}}={{U}_{L3}}=\frac{3}{4}{{U}_{L2}}=\frac{3}{4}{{U}_{L\max }}\) \(\Rightarrow \frac{U.{{Z}_{L1}}\cos {{\varphi }_{1}}}{R}=\frac{U.{{Z}_{L3}}\cos {{\varphi }_{3}}}{R}=\frac{3}{4}\frac{U.{{Z}_{L2}}\cos {{\varphi }_{2}}}{R}\)
\(\Rightarrow \omega _{1}^{2}{{\cos }^{2}}{{\varphi }_{1}}=\omega _{3}^{2}{{\cos }^{2}}{{\varphi }_{3}}=\frac{9}{16}\omega _{2}^{2}{{\cos }^{2}}{{\varphi }_{2}}\)
\(\Rightarrow \left\{ \begin{array}{*{35}{l}} \frac{{{\cos }^{2}}{{\varphi }_{1}}}{{{\cos }^{2}}{{\varphi }_{2}}}=\frac{9}{16}\frac{{{\omega }^{2}}}{\omega _{1}^{2}} \\ \frac{{{\cos }^{2}}{{\varphi }_{2}}}{{{\cos }^{2}}\varphi }=\frac{9}{16}\frac{{{\omega }^{2}}}{\omega _{2}^{2}} \\ \end{array}\Rightarrow \frac{{{\cos }^{2}}{{\varphi }_{1}}}{{{\cos }^{2}}{{\varphi }_{2}}}+\frac{{{\cos }^{2}}{{\varphi }_{3}}}{{{\cos }^{2}}{{\varphi }_{2}}}=\frac{9}{16}{{\omega }^{2}}\cdot \left( \frac{1}{\omega _{1}^{2}}+\frac{1}{\omega _{3}^{2}} \right) \right.\)
\(\Rightarrow \frac{{{\cos }^{2}}{{\varphi }_{1}}}{{{\cos }^{2}}{{\varphi }_{2}}}+\frac{{{\cos }^{2}}{{\varphi }_{2}}}{{{\cos }^{2}}{{\varphi }_{2}}}=\frac{9}{16}\omega _{2}^{2}\cdot \frac{2}{\omega _{2}^{2}}=\frac{9}{8}\text{ (1)}\)
Công suất tiêu thụ của mạch điện là: \(P=\frac{{{U}^{2}}{{\cos }^{2}}\varphi }{R}\Rightarrow P\sim {{\cos }^{2}}\varphi \)
Từ (1) ta có: \(\frac{{{P}_{1}}}{{{P}_{2}}}+\frac{{{P}_{3}}}{{{P}_{2}}}=\frac{9}{8}\Rightarrow \frac{{{P}_{1}}+{{P}_{3}}}{9}=\frac{{{P}_{2}}}{8}\)
Chọn B.
Cho đoạn mạch AB gồm đoạn AM nối tiếp với MB. Biết đoạn AM gồm điện trở R nối tiếp với tụ điện có điện dung C và MB chứa cuộn dây có độ tự cảm L và có điện trở r. Đặt vào AB một điện áp xoay chiều \(u=U\sqrt{2}\cos \omega \text{t (V)}\text{.}\) Biết \(R=r=\sqrt{\frac{L}{C}},\) điện áp hiệu dụng \({{U}_{MB}}=\sqrt{3}{{U}_{AM}}.\) Hệ số công suất của đoạn mạch gần với giá trị nào nhất sau đây?
Ta có: \(R=r=\sqrt{\frac{L}{C}}=\sqrt{{{Z}_{L}}.{{Z}_{C}}}\)
Theo đề bài có điện áp hiệu dụng:
\({{U}_{MB}}=\sqrt{3}{{U}_{AM}}\Rightarrow {{U}_{cd}}=\sqrt{3}{{U}_{RC}}\Rightarrow Z_{cd}^{2}=3{{Z}_{RC}}^{2}\)
\(\Rightarrow {{r}^{2}}+Z_{L}^{2}=3\left( {{R}^{2}}+Z_{C}^{2} \right)\Rightarrow {{R}^{2}}+Z_{L}^{2}=3{{R}^{2}}+3Z_{C}^{2}\)
\(\Rightarrow Z_{L}^{2}-2{{R}^{2}}-3Z_{C}^{2}=0\Rightarrow Z_{L}^{2}-2{{Z}_{L}}{{Z}_{C}}-3Z_{C}^{2}=0\)
\(\Rightarrow {{Z}_{L}}=3{{Z}_{C}}\)
Chuẩn hóa \({{Z}_{C}}=1\Rightarrow {{Z}_{L}}=3\Rightarrow R=r=\sqrt{3}\)
Hệ số công suất của mạch là:
\(\cos \varphi =\frac{R+r}{\sqrt{{{(R+r)}^{2}}+{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}}}=\frac{2\sqrt{3}}{\sqrt{{{(2\sqrt{3})}^{2}}+{{2}^{2}}}}\approx 0,866\)
Chọn D.

