Ôn tập chương 2: Động lực học chất điểm
I – TỔNG HỢP – PHÂN TÍCH LỰC
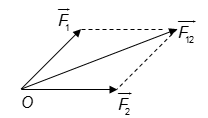
\(\overrightarrow {{F_{12}}} = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} \)
- Độ lớn: \({F^2} = F_1^2 + F_2^2 + 2{F_1}{F_2}cos\alpha \) với \(\alpha \) góc hợp bởi \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} \)
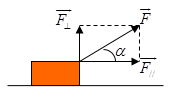
- Khi phân tích lực thành hai thành phần: $\left\{ \begin{array}{l}{F_{//}} = Fcos\alpha \\{F_ \bot } = F\sin \alpha \end{array} \right.$
II – BA ĐỊNH LUẬT NIU-TƠN
1. Định luật 1 Niuton: Khi một vật đứng yên hoặc chuyển động thẳng đều thì hợp lực của các lực tác dụng lên vật bằng 0.
\(\sum {\overrightarrow F = \overrightarrow 0 } \leftrightarrow \overrightarrow {{F_1}} + \overrightarrow {{F_2}} + ... + \overrightarrow {{F_n}} = \overrightarrow 0 \)
2. Định luật 2 Niuton: Véctơ gia tốc của một vật luôn cùng hướng với lực tác dụng lên vật. Độ lớn của véctơ gia tốc tỉ lệ thuận với độ lớn của véctơ lực tác dụng lên vật và tỉ lệ nghịch với khối lượng của vật.
\(\overrightarrow a = \dfrac{{\overrightarrow F }}{m}\) hay \(\overrightarrow F = m\overrightarrow a \)
3. Định luật 3 Niuton: Khi vật A tác dụng lên vật B một lực, thì vật B cũng tác dụng trở lại vật A một lực. Hai lực này là hai lực trực đối.
\({\overrightarrow F _{AB}} = - {\overrightarrow F _{BA}}\)
III – CÁC LOẠI LỰC
1. Lực hấp dẫn
Lực hấp dẫn giữa hai vật (coi như chất điểm) tỉ lệ thuần với tích của hai khối lượng của chúng và tỉ lệ nghịch với bình phương khoảng cách giữa chúng.
\({F_{h{\rm{d}}}} = G\dfrac{{{m_1}{m_2}}}{{{r^2}}}\)
Trong đó:
+ $G{\rm{ }} = {\rm{ }}6,{67.10^{ - 11}}N.{m^2}/kg$ : hằng số hấp dẫn
+${m_1},{\rm{ }}{m_2}$ : là khối lượng của hai vật
+$r$ : khoảng cách giữa hai vật
+ Khoảng cách $r$ được tính từ tâm vật này đến tâm vật kia
+ Lực hấp dẫn của hai chất điểm là cặp lực trực đối
2. Lực đàn hồi
Lực đàn hồi là lực xuất hiện khi một vật bị biến dạng đàn hồi và có xu hướng chống lại nguyên nhân gây ra biến dạng.
Trong giới hạn đàn hồi, lực đàn hồi của lò xo tỉ lệ thuận với độ biến dạng của lò xo: \({F_{dh}} = - k\Delta l\)
- Phương: trùng với phương của trục lò xo
- Chiều: ngược với chiều biến dạng của lò xo
- Độ lớn: \({F_{dh}} = k\left| {\Delta l} \right|\)
Trong đó:
+ \(\Delta l\): độ biến dạng của lò xo
+ k: hệ số đàn hồi (N/m)
+ Dấu “-“ chỉ rằng, lực đàn hồi luôn ngược hướng với chiều biến dạng
3. Lực ma sát
- Ma sát nghỉ: xuất hiện khi một vật đứng yên mà vẫn chịu tác dụng của lực.
+ Độ lớn: Lực ma sát nghỉ có độ lớn bằng độ lớn ngoại lực tác dụng vào vật trên phương song song với mặt tiếp xúc
Chú ý:
+ Lực ma sát nghỉ không có biểu thức.
+ Lực ma sát nghỉ cực đại: \({F_{ms{n_{{\rm{max}}}}}} = {\mu _n}.N\)
- Ma sát trượt: xuất hiện khi một vật trượt trên bề mặt của vật khác. ${F_{mst}} = {\mu _t}.N$
- Ma sát lăn: xuất hiện khi một vật lăn trên bề mặt của vật khác. ${F_{msl}} = {\mu _l}.N$
4. Lực quán tính
Lực quán tính là lực sinh ra trong hệ quy chiếu phi quán tính, lực quán tính cũng gây biến dạng và gia tốc cho vật.
Lực quán tính không có phản lực.
\(\overrightarrow {{F_{qt}}} = - m\overrightarrow a \)
Trong đó:
+ \(m\): khối lượng của vật $\left( {kg} \right)$
+ \(a\): gia tốc của hệ quy chiếu chuyến động $\left( {m/{s^2}} \right)$
5. Lực hướng tâm (đây không phải loại lực cơ học mới như ma sát, đàn hồi, hấp dẫn)
Hợp lực của các lực tác dụng vào vật làm vật chuyển động tròn đều gọi là lực hướng tâm:
\(\overrightarrow {{F_{ht}}} = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} + ... + \overrightarrow {{F_n}} \)
Với \({F_{ht}} = m{a_{ht}} = m\dfrac{{{v^2}}}{r} = m{\omega ^2}r\)
Công thức liên hệ: với $\omega $: tốc độ góc $\left( {rad/s} \right)$, $f$: tần số \(Hz\), $T$: chu kì $\left( s \right)$
Chú ý: $r$ - là khoảng cách từ vật đến tâm quay của vật
IV – CHUYỂN ĐỘNG CỦA VẬT BỊ NÉM
Bài toán vật bị ném ngang từ độ cao h:
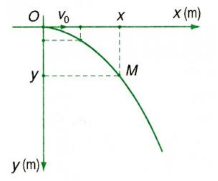
(Chọn trục tọa độ Oxy như hình vẽ)
Trên trục Ox: Vật chuyển động thẳng đều: \(\left\{ \begin{array}{l}x = {v_0}t{\rm{ }}\left( 1 \right)\\{v_x} = {v_0}{\rm{ }}\left( 2 \right)\end{array} \right.\)
Trên trục Oy: Xem như vật rơi tự do với gia tốc g: \(\left\{ \begin{array}{l}y = \dfrac{1}{2}g{t^2}{\rm{ }}\left( 3 \right)\\{v_y} = gt{\rm{ }}\left( 4 \right)\end{array} \right.\)
* Tìm thời gian rơi: \(t = \sqrt {\dfrac{{2h}}{g}} \)
* Tìm vận tốc ở độ cao h1 so với mặt đất (h1<h): \(v = \sqrt {v_x^2 + v_y^2} \)
Với ${v_x} = {\rm{ }}{v_0}$, ${v_y}$ được tìm như sau: cho y = h1 giải PT (3) tìm thời gian t, sau đó thế t vào PT (4) tìm ${v_y}$
* Tìm tầm ném xa: \(L = {v_0}\sqrt {\dfrac{{2h}}{g}} \)
