Va chạm đàn hồi - Va chạm mềm

Lý thuyết Va chạm mềm - Va chạm đàn hồi, cách xác định vận tốc của vật trước và sau va chạm.
(387) 1290 29/07/2022
Bài viết đã được lưu
Chia sẻ

Nội dung bài viết

    Xem thêm

    I - VA CHẠM MỀM (VA CHẠM KHÔNG ĐÀN HỒI)

    Va chạm mềm là va chạm  mà sau khi va chạm hai vật gắn chặt vào nhau và chuyển động với cùng vận tốc:

    \({m_1}{v_1} + {m_2}{v_2} = \left( {{m_1} + {m_2}} \right)V\)

    Trong đó:

         + \({m_1},{m_2}\): khối lượng của vật 1 và vật 2

         + \({v_1},{v_2}\): vận tốc trước va chạm của vật 1 và vật 2

         + \(V\): vận tốc sau va chạm của 2 vật

    Chú ý: \({v_1},{v_2},V\) là các giá trị đại số có thể âm, dương hoặc bằng 0 tùy vào từng trường hợp cụ thể và hệ quy chiếu ta chọn.

    II - VA CHẠM ĐÀN HỔI (Đọc thêm)

    Va chạm đàn hồi là va chạm xuất hiện biến dạng đàn hồi trong khoảng thời gian rất ngắn, sau va chạm vật lấy lại hình dạng ban đầu và tiếp tục chuyển động tách rời nhau.

    1. Va chạm đàn hồi trực diện xuyên tâm

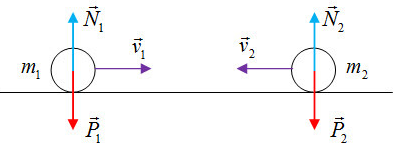
    + Bảo toàn động lượng: \(\overrightarrow {{P_1}}  + \overrightarrow {{P_2}}  = \overrightarrow {P{'_1}}  + \overrightarrow {P{'_2}} \)

    hay \({m_1}{v_1} + {m_2}{v_2} = {m_1}v{'_1} + {m_2}v{'_2}\)  (1)

    với \({v_1},{v_2},v{'_1},v{'_2}\) là các giá trị đại số có thể âm, dương hoặc bằng 0 tùy vào từng trường hơp cụ thể và hệ quy chiếu ta chọn.

    + Bảo toàn động năng:

    \({{\rm{W}}_{{{\rm{d}}_1}}} + {{\rm{W}}_{{d_2}}} = {{\rm{W}}_{d{'_1}}} + {{\rm{W}}_{d{'_2}}}\)
    \( \Leftrightarrow \dfrac{1}{2}{m_1}v_1^2 + \dfrac{1}{2}{m_2}v_2^2 = \dfrac{1}{2}{m_1}{v'}_1^2 + \dfrac{1}{2}{m_2}{v'}_2^2{\rm{ }}\left( 2 \right)\)

    Từ (1) và (2), ta suy ra:

    \(\left\{ \begin{array}{l}v{'_1} = \frac{{\left( {{m_1} - {m_2}} \right){v_1} + 2{m_2}{v_2}}}{{{m_1} + {m_2}}}\\v{'_2} = \frac{{\left( {{m_2} - {m_1}} \right){v_2} + 2{m_1}{v_1}}}{{{m_1} + {m_2}}}\end{array} \right.\)  

    2. Các trường hợp đặc biệt của va chạm đàn hồi xuyên tâm:

    + Hai vật có khối lượng bằng nhau: \({m_1} = {m_2}\)

    Ta suy ra: \(\left\{ \begin{array}{l}v{'_1} = {v_2}\\v{'_2} = {v_1}\end{array} \right.\)

    Điều này có nghĩa là sau va chạm chuyển động của vật \({m_1}\) sẽ truyền cho vật \({m_2}\) và chuyển động của vật \({m_2}\) truyền cho vật \({m_1}\)

    + Vật \({m_1}\) có khối lượng rất nhỏ so với vật \({m_2}\) và ban đầu vật \({m_2}\) có \({v_2} = 0\) (đứng yên)

    \({m_1} \ll {m_2} \to \frac{{{m_1}}}{{{m_2}}} \approx 0\)

    thay vào biểu thức tổng quát trên, ta suy ra: \(\left\{ \begin{array}{l}v{'_1} =  - {v_1}\\v{'_2} = 0\end{array} \right.\)

    Có nghĩa là sau va chạm, vật \({m_2}\) vẫn nằm yên còn vật \({m_1}\) bị bật ngược trở lại

    Xem toàn bộ nội dung Vật lý 10:

    (387) 1290 29/07/2022
    Bài viết đã được lưu
    Bài trước
    Chia sẻ
    Bài sau  
    Tìm thêm: Lý thuyết Lý thuyết lớp 10 Vật lý 10