Phương pháp giải bài tập ba định luật Newton

PHƯƠNG PHÁP CHUNG

- Vận dụng định nghĩa về các định luật Niutơn

Bài tập định luật I Niutơn

\(\overrightarrow F  = 0 \Rightarrow \overrightarrow a  = 0\):

Suy ra: v = 0 (đứng yên) hoặc v không đổi (chuyển động thẳng đều).

Nếu vật chịu tác dụng của nhiều lực thì \(\overrightarrow F  = \overrightarrow {{F_{hl}}}  = \overrightarrow {{F_1}}  + \overrightarrow {{F_2}}  + ... + \overrightarrow {{F_n}} \)

Bài tập định luật II Niutơn

- Xác định gia tốc hay lực, áp dụng biểu thức định II - Niutơn: \(F = ma\)

- Phân tích lực, vận dụng định luật II - Niutơn

Các bước giải:

- Bước 1: Phân tích các lực tác dụng vào vật

- Bước 2: gắn hệ trục tọa độ, chọn chiều dương

- Bước 3: Tính toán các yêu cầu của đề bài

Bài tập định luật III Niutơn

- Công thức vận dụng định luật III - Niutơn

\(\begin{array}{l}{\overrightarrow F _{12}} =  - {\overrightarrow F _{21}} \to {m_1}\overrightarrow {{a_1}}  =  - {m_2}\overrightarrow {{a_2}} \\ \leftrightarrow {m_1}\frac{{\overrightarrow {{v_1}}  - \overrightarrow {{v_{01}}} }}{{\Delta t}} =  - {m_2}\frac{{\overrightarrow {{v_2}}  - \overrightarrow {{v_{02}}} }}{{\Delta t}}\end{array}\)

Trong đó:

• \({v_1},{v_{01}}\): lần lượt là vận tốc của vật m₁ trước và sau va chạm
• \({v_2},{v_{02}}\): lần lượt là vận tốc của vật m₂ trước và sau va chạm

PHƯƠNG PHÁP ĐỘNG HỌC

Bước 1: Chọn vật (hệ vật) khảo sát.

Bước 2: Chọn hệ quy chiếu gắn với vật (cụ thể hóa bằng hệ trục tọa độ vuông góc; trục tọa độ Ox luôn trùng với phương chiều chuyển động, trục tọa độ Oy vuông góc với phương chuyển động).

Bước 3: Xác định các lực và biểu diễn các lực tác dụng lên vật trên hình vẽ (phân tích lực có phương không song song hoặc vuông góc với bề mặt tiếp xúc).

Bước 4: Viết phương trình hợp lực tác dụng lên vật theo định luật II Niutơn.

\(\overrightarrow {{F_{hl}}}  = \sum\limits_{i = 1}^n {\overrightarrow {{F_i}} }  = \overrightarrow {{F_1}}  + \overrightarrow {{F_2}}  + ... + \overrightarrow {{F_n}}  = m\overrightarrow a \) (*)

Bước 5: Chiếu phương trình (*) lên các trục tọa độ Ox, Oy:

\(\left\{ \begin{array}{l}Ox:{F_{1{\rm{x}}}} + {F_{2{\rm{x}}}} + ... + {F_{n{\rm{x}}}} = ma\left( 1 \right)\\Oy:{F_{1y}} + {F_{2y}} + ... + {F_{ny}} = 0\left( 2 \right)\end{array} \right.\)

PHƯƠNG PHÁP CHIẾU

- Nếu lực vuông góc với phương chiếu thì độ lớn đại số của F trên phương đó bằng 0

- Nếu lực song song với phương chiếu thì độ lớn đại số của F trên phương chiếu đó bằng:

+ Trường hợp 1: F cùng hướng với chiều dương phương chiếu:

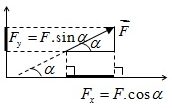
+ Trường hợp 2: F ngược hướng với chiều dương phương chiếu:

Giải phương trình (1) và (2) ta được các đại lượng cần tìm.