Lời giải của giáo viên
 HocOn247.com
HocOn247.com
Ta có: \(y = f\left( {{x^2} + m} \right) \Rightarrow y' = 2x.f'\left( {{x^2} + m} \right)\)
\(y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\f'\left( {{x^2} + m} \right) = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 0\\{x^2} + m = 0\\{x^2} + m = 3\end{array} \right.\) (do tại \(x = 1\) ta có\(y = f'(x)\) không đổi dấu) \( \Leftrightarrow \left[ \begin{array}{l}x = 0\\{x^2} = - m\\{x^2} = 3 - m\end{array} \right.\)
+) \(m = 0\) ta có \(y' = 0 \Rightarrow \left[ \begin{array}{l}x = 0\\x = \pm \sqrt 3 \end{array} \right.\)
\(y' = 0\) tại 3 điểm \(x = 0,\,\,x = \sqrt 3 ,\,\,x = - \sqrt 3 \) và đổi dấu tại 3 điểm này \( \Rightarrow m = 0\) thỏa mãn
+) \(m = 3\) ta có \(y' = 0 \Leftrightarrow x = 0\)\( \Rightarrow m = 3\) không thỏa mãn
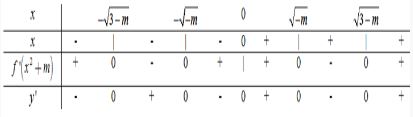
+) \(m < 0\)
\(y' = 0\) có 5 nghiệm phân biệt \(x = 0,\,x = \pm \sqrt { - m} ,\,\,\,x = \pm \sqrt {3 - m} \)
Hàm số có 5 cực trị \( \Rightarrow \) Loại các giá trị \(m < 0\).
+) \(m > 3\)
Phương trình \(y' = 0\) có 1 nghiệm duy nhất \(x = 0\) và đổi dấu tại 1 điểm duy nhất \(x = 0\) \( \Rightarrow \) Loại các giá trị \(m > 3\)
+) \(0 < m < 3\)
\(y' = 0\) có 3 nghiệm phân biệt \(x = 0,\,\,\,x = \pm \sqrt {3 - m} \)
Hàm số có 3 cực trị \(x = 0,\,\,\,x = \pm \sqrt {3 - m} \)\( \Rightarrow \) Các giá trị \(0 < m < 3\) thỏa mãn
Mà \(m \in Z \Rightarrow m \in \left\{ {1;2} \right\}\)
Kết luận: Để hàm số \(y = f({x^2} + m)\) có \(3\) điểm cực trị thì \(m \in \left\{ {0;1;2} \right\}\): có 3 giá trị m thỏa mãn.
Chọn: A
CÂU HỎI CÙNG CHỦ ĐỀ
Cho khối chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D; AB = AD = 2a;CD = a . Góc giữa hai mặt phẳng (SBC) và (ABCD) bằng 600 . Gọi I là trung điểm của AD. Biết 2 mặt phẳng (SBI) và (SCI) cùng vuông góc với mặt phẳng (ABCD). Tính thể tích khối chóp S.ABCD.
Đồ thị sau đây là của hàm số\(y = {x^4} - 3{x^2} - 3\). Với giá trị nào của m thì phương trình \({x^4} - 3{x^2} + m = 0\)có ba nghiệm phân biệt ?
Cho hàm số \(y = \dfrac{{2x + 1}}{{x - 1}}\) xác định trên R\{1} . Đạo hàm của hàm số là:
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(a\), tâm \(O\). Cạnh bên \(SA = 2a\) và vuông góc với mặt đáy \(\left( {ABCD} \right)\). Gọi \(H\) và \(K\) lần lượt là trung điểm của cạnh \(BC\) và \(CD\). Tính khoảng cách giữa hai đường thẳng \(HK\) và \(SD\).
Có 5 học sinh lớp 12A1, 3 học sinh lớp 12A2, 2 học sinh lớp 12D1. Xếp ngẫu nhiên 10 học sinh trên thành một hàng dài. Tính xác suất để trong 10 học sinh trên không có hai học sinh cùng lớp đứng cạnh nhau.
Cho hàm số \(y = f(x)\), biết rằng hàm số \(y = f'(x - 2) + 2\) có đồ thị như hình vẽ bên. Hỏi hàm số \(y = f(x)\) nghịch biến trên khoảng nào trong các khoảng dưới đây?
Tính đạo hàm của hàm số \(f\left( x \right) = x\left( {x - 1} \right)\left( {x - 2} \right)...\left( {x - 2018} \right)\) tại điểm \(x = 0\).
Trong mặt phẳng với hệ tọa độ Oxy, cho hình vuông ABCD. Gọi M(1;3) là trung điểm của cạnh BC, \(N\left( { - \dfrac{3}{2};\dfrac{1}{2}} \right)\) là điểm trên cạnh AC sao cho \(AN = \dfrac{1}{4}AC\) . Xác định tọa độ điểm D, biết D nằm trên đường thẳng \(x - y - 3 = 0\)
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông, \(SA \bot \left( {ABCD} \right).\) Khẳng định nào dưới đây sai?
Cho tam giác ABC vuông cân tại A có BC =2. Tính tích vô hướng \(\overrightarrow {AB} .\overrightarrow {CA} \):
Cho hàm số \(y = f(x)\)có đồ thị như hình vẽ dưới đây. Hàm số \(y = f(x)\)có bao nhiêu điểm cực tiểu?
Gọi giá trị lớn nhất và nhỏ nhất của hàm số \(y = {x^4} + 2{x^2} - 1\) trên đoạn \(\left[ { - 1;2} \right]\) lần lượt là \(M\) và \(m\). Khi đó, giá trị của \(M.m\) là:
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số \(f\left( x \right) = 2{\cos ^3}x - \cos 2x\) trên tập hợp \(D = \left[ { - \dfrac{\pi }{3};\dfrac{\pi }{3}} \right]\)

.JPG)

.JPG)
.JPG)
.JPG)
.JPG)



