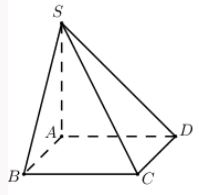
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(a\), cạnh bên \(SA\) vuông góc với đáy \(\left( {ABCD} \right)\). Biết góc tạo bởi hai mặt phẳng \(\left( {SBC} \right)\) và \(\left( {ABCD} \right)\) bằng \(60^\circ \). Tính thể tích \(V\) của khối chóp \(S.ABCD\).
A. \(V = {a^3}\sqrt 3 \).
B. \(V = \dfrac{{{a^3}\sqrt 3 }}{3}\).
C. \(V = \dfrac{{{a^3}\sqrt 3 }}{{12}}\).
D. \(V = \dfrac{{{a^3}\sqrt 3 }}{{24}}\).
Lời giải của giáo viên
 HocOn247.com
HocOn247.com
Ta có: \(\left\{ \begin{array}{l}BC \bot AB\\BC \bot SA\end{array} \right. \Rightarrow BC \bot \left( {SAB} \right) \Rightarrow BC \bot SB\)
\(\left\{ \begin{array}{l}\left( {SBC} \right) \cap \left( {ABCD} \right) = BC\\\left( {SBC} \right) \supset SB \bot BC\\\left( {ABCD} \right) \supset AB \bot BC\end{array} \right. \Rightarrow \angle \left( {\left( {SBC} \right);\left( {ABCD} \right)} \right) = \angle \left( {SB;AB} \right) = \angle SBA = {60^0}\)
Ta có: \(SA = AB\tan 60 = a\sqrt 3 \)\( \Rightarrow {V_{S.ABCD}} = \dfrac{1}{3}SA.{S_{ABCD}} = \dfrac{1}{3}.a\sqrt 3 .{a^2} = \dfrac{{{a^3}\sqrt 3 }}{3}\).
Chọn B.
CÂU HỎI CÙNG CHỦ ĐỀ
Hàm số \(y = {x^4} - 8{x^2} - 4\) nghịch biến trên các khoảng.
Phương trình tiếp tuyến với đồ thị hàm số \(y = \dfrac{{x + 1}}{{x - 1}}\) song song với đường thẳng \(\left( \Delta \right):\,\,2x + y + 1 = 0\) là.
Cho hàm số \(f\left( x \right)\) xác định trên R và có đồ thị hàm số \(y = f'\left( x \right)\) là đường cong trong hình bên. Mệnh đề nào dưới đây đúng?
Hàm số liên tục trên R và có bảng biến thiên như hình vẽ. Mệnh đề nào sau đây là đúng?
Hàm số \(y = \dfrac{{2x - 1}}{{x + 1}}\). Khẳng định nào sau đây đúng.
Số đường tiệm cận của đồ thị hàm số\(y = \dfrac{{{x^2} - 3x + 2}}{{{x^2} - 4}}\) là.
Cho hình chóp tam giác \(S.ABC\)với \(ABC\)là tam giác đều cạnh \(a\). \(SA \bot (ABC)\) và \(SA = a\sqrt 3 .\) Tính thể tích của khối chóp \(S.ABC\).
Phương trình tiếp tuyến của đồ thị hàm số \(y = {x^3} - 3{x^2} - x + 3\) tại điểm \(M\left( {1;0} \right)\) là.
Cho đồ thị của hàm số \(y = {x^3} - 6{x^2} + 9x - 2\) như hình vẽ. Khi đó phương trình \(\left| {{x^3} - 6{x^2} + 9x - 2} \right| = m\) (m là tham số) có 6 nghiệm phân biệt khi và chỉ khi.
Cho \(\sin \alpha = \dfrac{1}{3}\)và \(\dfrac{\pi }{2} < \alpha < \pi \). Khi đó \(\cos \alpha \) có giá trị là.
Khoảng cách từ \(I(1; - 2)\) đến đường thẳng \(\Delta :3x - 4y - 26 = 0\) bằng.
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình chữ nhật, \(AB = a,{\rm{ }}AD = 2a\), \(SA\) vuông góc với mặt phẳng\(\left( {ABCD} \right)\), \(SA = a\sqrt 3 \). Thể tích của khối chóp \(S.ABCD\) là.
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. SA\( \bot \)(ABCD) và \(SB = \sqrt 3 \). Thể tích khối chóp S.ABCD là.
Cho khối lập phương \(ABCD.A'B'C'D'\) cạnh \(a\). Các điểm E và \(F\) lần lượt là trung điểm của C’B’ và C’D’. Mặt phẳng (AEF) cắt khối lập phương đã cho thành hai phần, gọi \({V_1}\) là thể tích khối chứa điểm A’ và \({V_2}\) là thể tích khối chứa điểm C’. Khi đó \(\dfrac{{{V_1}}}{{{V_2}}}\) là.

.JPG)
.JPG)
.JPG)



