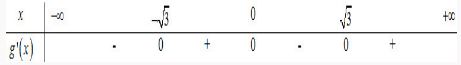Đề thi thử THPT QG năm 2022 môn Toán - Trường THPT Thanh Xuân
Đề thi thử THPT QG năm 2022 môn Toán
-
Hocon247
-
50 câu hỏi
-
90 phút
-
176 lượt thi
-
Trung bình
Tham gia [ Hs Hocon247.com ] - Cộng Đồng Luyện Thi Trực Tuyến để được học tập những kiến thức bổ ích từ HocOn247.com
Hàm số liên tục trên R và có bảng biến thiên như hình vẽ. Mệnh đề nào sau đây là đúng?
Dựa vào BBT của hàm số ta có \({x_{CD}} = 1,\,\,{x_{CT}} = 2\).
Do đó hàm số đã cho có 2 điểm cực trị.
Chọn A.
Cho hàm số \(y = \dfrac{{2x}}{{x + 2}}\) có đồ thị \((C)\). Viết phương trình tiếp tuyến của \((C)\), biết tiếp tuyến tạo với hai trục tọa độ một tam giác có diện tích bằng \(\dfrac{1}{{18}}\).
TXĐ: \(D = R\backslash \left\{ { - 2} \right\}\). Ta có: \(y' = \dfrac{4}{{{{\left( {x + 2} \right)}^2}}}\).
Phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ \(x = {x_0}\) là: \(y = \dfrac{4}{{{{\left( {{x_0} + 2} \right)}^2}}}\left( {x - {x_0}} \right) + \dfrac{{2{x_0}}}{{{x_0} + 2}}\,\,\left( d \right)\)
Gọi \(A = d \cap Ox\). Cho \(y = 0 \Rightarrow \dfrac{{4\left( {x - {x_0}} \right)}}{{{{\left( {{x_0} + 2} \right)}^2}}} + \dfrac{{2{x_0}}}{{{x_0} + 2}} = 0 \Leftrightarrow 4x - 4{x_0} + 2x_0^2 + 4{x_0} = 0 \Leftrightarrow x = \dfrac{{x_0^2}}{2} \Rightarrow A\left( {\dfrac{{x_0^2}}{2};0} \right)\)
\( \Rightarrow OA = \dfrac{{x_0^2}}{2}\) .
Gọi \(B = d \cap Oy\). Cho \(x = 0 \Rightarrow y = \dfrac{{ - 4{x_0}}}{{{{\left( {{x_0} + 2} \right)}^2}}} + \dfrac{{2{x_0}}}{{{x_0} + 2}} = \dfrac{{ - 4{x_0} + 2x_0^2 + 4{x_0}}}{{{{\left( {{x_0} + 2} \right)}^2}}} = \dfrac{{2x_0^2}}{{{{\left( {{x_0} + 2} \right)}^2}}} \Rightarrow B\left( {0;\dfrac{{2x_0^2}}{{{{\left( {{x_0} + 2} \right)}^2}}}} \right)\)
\( \Rightarrow OB = \dfrac{{2x_0^2}}{{{{\left( {{x_0} + 2} \right)}^2}}}\)
\(\begin{array}{l} \Rightarrow {S_{\Delta OAB}} = \dfrac{1}{2}OA.OB = \dfrac{1}{2}.\dfrac{{x_0^2}}{2}.\dfrac{{2x_0^2}}{{{{\left( {{x_0} + 2} \right)}^2}}} = \dfrac{1}{{18}}\\ \Leftrightarrow 9x_0^4 = {\left( {{x_0} + 2} \right)^2} \Leftrightarrow \left[ \begin{array}{l}3x_0^2 = {x_0} + 2\\3x_0^2 = - {x_0} - 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}{x_0} = 1\\{x_0} = \dfrac{{ - 2}}{3}\end{array} \right.\end{array}\)
Vậy có 2 tiếp tuyến thỏa mãn là \(\left[ \begin{array}{l}y = \dfrac{4}{9}x + \dfrac{2}{9}\\y = \dfrac{9}{4}x + \dfrac{1}{2}\end{array} \right.\) .
Chọn A.
Cho hàm số\(y = (x - 2)({x^2} - 5x + 6)\) có đồ thị \(\left( C \right)\). Mệnh đề nào dưới đây đúng.
Xét phương trình hoành độ giao điểm \(\left( {x - 2} \right)\left( {{x^2} - 5x + 6} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 2\\x = 3\end{array} \right.\).
Vậy đồ thị \(\left( C \right)\) cắt trục hoành tại 2 điểm phân biệt.
Chọn D.
Hàm số \(y = {x^4} - 8{x^2} - 4\) nghịch biến trên các khoảng.
TXĐ: \(D = R\). Ta có: \(y' = 4{x^3} - 16x < 0 \Leftrightarrow 4x\left( {{x^2} - 4} \right) < 0 \Leftrightarrow x \in \left( { - \infty ; - 2} \right) \cup \left( {0;2} \right)\).
Vậy hàm số nghịch biến trên \(\left( { - \infty ; - 2} \right)\) và \(\left( {0;2} \right)\).
Chọn B.
Cho khai triển \({\left( {1 - 2x} \right)^n} = {a_0} + {a_1}x + {a_2}{x^2} + ... + {a_n}{x^n}\) biết \(S = \left| {{a_1}} \right| + 2\left| {{a_2}} \right| + ... + n\left| {{a_n}} \right| = 34992\). Tính giá trị của biểu thức \(P = {a_0} + 3{a_1} + 9{a_2} + ... + {3^n}{a_n}\)
Ta có: \({\left( {1 - 2x} \right)^n} = \sum\limits_{k = 0}^n {C_n^k{{\left( { - 2x} \right)}^k}} = \sum\limits_{k = 0}^n {C_n^k{{\left( { - 2} \right)}^k}{x^k}} \)
\( \Rightarrow {a_k} = C_n^k.{\left( { - 2} \right)^k} \Rightarrow \left| {{a_k}} \right| = C_n^k{.2^k}\,\,\forall k = \overline {0;n} \).
Khi đó ta có:
\(S = \left| {{a_1}} \right| + 2\left| {{a_2}} \right| + ... + n\left| {{a_n}} \right| = C_n^1{.2^1} + 2.C_n^2{.2^2} + .... + n.C_n^n{.2^n}\)
Xét khai triển
\(\begin{array}{l}{\left( {1 + x} \right)^n} = \sum\limits_{i = 0}^n {C_n^i.{x^i}} = C_n^0 + C_n^1x + C_n^2{x^2} + ... + C_n^n{x^n}\\ \Rightarrow n{\left( {1 + x} \right)^{n - 1}} = C_n^1 + 2C_n^2x + ... + nC_n^n{x^{n - 1}}\end{array}\)
Thay \(x = 2\) ta có \(n{.3^{n - 1}} = C_n^1 + 2C_n^2.2 + ... + nC_n^n{.2^{n - 1}} \Rightarrow 2.n{.3^{n - 1}} = 2C_n^1 + 2C_n^2{.2^2} + ... + nC_n^n{.2^n}\)
\( \Rightarrow S = 2n{.3^{n - 1}} = 34992 \Leftrightarrow n{.3^{n - 1}} = 17496 \Leftrightarrow n = 8\).
Thay \(n = 8\) vào P ta có
\(\begin{array}{l}P = {a_0} + 3{a_1} + 9{a_2} + ... + {3^8}{a_8}\\P = C_8^0 + 3.C_8^1.{\left( { - 2} \right)^1} + {3^2}.C_8^2.{\left( { - 2} \right)^2} + ... + {3^8}.C_8^8.{\left( { - 2} \right)^8}\\P = C_8^0 - C_8^1{.6^1} + C_8^2{.6^2} - .... + C_8^8{.6^8}\\P = {\left( {1 - 6} \right)^8} = {5^8} = 390625\end{array}\)
Chọn D.
Số đường tiệm cận của đồ thị hàm số\(y = \dfrac{{{x^2} - 3x + 2}}{{{x^2} - 4}}\) là.
Ta có: \(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to - \infty } y = 1 \Rightarrow y = 1\) là TCN của đồ thị hàm số.
Có \(y = \dfrac{{{x^2} - 3x + 2}}{{{x^2} - 4}} = \dfrac{{\left( {x - 2} \right)\left( {x - 1} \right)}}{{\left( {x - 2} \right)\left( {x + 2} \right)}} = \dfrac{{x - 1}}{{x + 2}} \Rightarrow x = - 2\) là TCĐ của đồ thị hàm số.
Vậy đồ thị hàm số đã cho có 2 đường tiệm cận.
Chọn A.
Cho đồ thị của hàm số \(y = {x^3} - 6{x^2} + 9x - 2\) như hình vẽ. Khi đó phương trình \(\left| {{x^3} - 6{x^2} + 9x - 2} \right| = m\) (m là tham số) có 6 nghiệm phân biệt khi và chỉ khi.
Từ đồ thị hàm số \(y = {x^3} - 6{x^2} + 9x - 2\) ta suy ra đồ thị hàm số \(y = \left| {{x^3} - 6{x^2} + 9x - 2} \right|\) như sau:
Số nghiệm của phương trình \(\left| {{x^3} - 6{x^2} + 9x - 2} \right| = m\) là số giao điểm của đồ thị hàm số \(y = \left| {{x^3} - 6{x^2} + 9x - 2} \right|\) và đường thẳng \(y = m\) song song với trục hoành.
Dựa vào đồ thị hàm số ta thấy: Để phương trình có 6 nghiệm phân biệt \( \Leftrightarrow 0 < m < 2\).
Chọn B.
Cho khối lập phương \(ABCD.A'B'C'D'\) cạnh \(a\). Các điểm E và \(F\) lần lượt là trung điểm của C’B’ và C’D’. Mặt phẳng (AEF) cắt khối lập phương đã cho thành hai phần, gọi \({V_1}\) là thể tích khối chứa điểm A’ và \({V_2}\) là thể tích khối chứa điểm C’. Khi đó \(\dfrac{{{V_1}}}{{{V_2}}}\) là.
Gọi \(G = EF \cap A'B',\,\,H = EF \cap A'D',\,\,M = AG \cap BB',\,\,N = AH \cap DD'\).
Khi đó ta có \({V_1} = {V_{A.A'GH}} - {V_{M.B'GE}} - {V_{N.D'FH}}\)
Áp dụng định lí Ta-lét ta có: \(\dfrac{{B'G}}{{C'F}} = \dfrac{{B'E}}{{C'E}} = 1 \Rightarrow B'G = C'F = \dfrac{a}{2}\).
\( \Rightarrow {S_{B'GE}} = \dfrac{1}{2}B'G.B'E = \dfrac{1}{2}.\dfrac{a}{2}.\dfrac{a}{2} = \dfrac{{{a^2}}}{8}\).
Áp dụng định lí Ta-lét ta lại có \(\dfrac{{MB'}}{{AA'}} = \dfrac{{GB'}}{{GA'}} = \dfrac{1}{3} \Rightarrow MB' = \dfrac{1}{3}AA' = \dfrac{a}{3}\).
\( \Rightarrow {V_{M.B'GE}} = \dfrac{1}{3}.\dfrac{a}{3}.\dfrac{{{a^2}}}{8} = \dfrac{{{a^3}}}{{72}}\). Hoàn toàn tương tự ta chứng minh được \({S_{D'FH}} = \dfrac{{{a^2}}}{8};\,\,ND' = \dfrac{a}{3} \Rightarrow {V_{N.D'FH}} = \dfrac{{{a^3}}}{{72}}\). Ta có: \({S_{A'GH}} = {S_{A'B'C'D'}} + {S_{B'GE}} + {S_{D'FH}} - {S_{C'EF}} = {a^2} + \dfrac{{{a^2}}}{8} + \dfrac{{{a^2}}}{8} - \dfrac{{{a^2}}}{8} = \dfrac{{9{a^2}}}{8}\)
\( \Rightarrow {V_{A.A'GH}} = \dfrac{1}{3}.a.\dfrac{{9{a^2}}}{8} = \dfrac{{3{a^3}}}{8}\).
\(\begin{array}{l} \Rightarrow {V_1} = {V_{A.A'GH}} - {V_{M.B'GE}} - {V_{N.D'FH}} = \dfrac{{3{a^3}}}{8} - \dfrac{{{a^3}}}{{72}} - \dfrac{{{a^3}}}{{72}} = \dfrac{{25{a^3}}}{{72}}\\ \Rightarrow {V_2} = {V_{ABCD.A'B'C'D'}} - {V_1} = {a^3} - \dfrac{{25{a^3}}}{{72}} = \dfrac{{47{a^3}}}{{72}}\end{array}\)
Vậy \(\dfrac{{{V_1}}}{{{V_2}}} = \dfrac{{25}}{{47}}\).
Chọn A.
Gọi \(\left( {x;y} \right)\) là nghiệm dương của hệ phương trình \(\left\{ \begin{array}{l}\sqrt {x + y} + \sqrt {x - y} = 4\\{x^2} + {y^2} = 128\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\end{array} \right.\). Tổng \(x + y\) bằng:
\(\left\{ \begin{array}{l}x + y \ge 0\\x - y \ge 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge - y\\x \ge y\\x \ge 0\end{array} \right.\)
Từ phương trình thứ nhất ta có
\(\begin{array}{l}\,\,\,\,\,\sqrt {x + y} + \sqrt {x - y} = 4 \Leftrightarrow x + y + x - y + 2\sqrt {{x^2} - {y^2}} = 16\\ \Leftrightarrow \sqrt {{x^2} - {y^2}} = 8 - x \Leftrightarrow \left\{ \begin{array}{l}8 - x \ge 0\\{x^2} - {y^2} = {x^2} - 16x + 64\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \le 8\\{y^2} = 16x - 64\end{array} \right.\end{array}\)
Thế \({y^2} = 16x - 64\) vào phương trình thứ hai ta có :
\({x^2} + 16x - 64 = 128 \Leftrightarrow \left[ \begin{array}{l}x = 8\,\,\,\,\,\,\,\left( {tm} \right)\\x = - 24\,\,\left( {ktm} \right)\end{array} \right. \Rightarrow {y^2} = 16.8 - 64 = 64 \Leftrightarrow y = 8\,\,\left( {Do\,\,y > 0} \right)\).
Vậy nghiệm dương của hệ phương trình là \(\left( {x;y} \right) = \left( {8;8} \right) \Rightarrow x + y = 16\).
Chọn C.
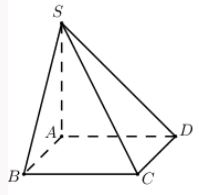
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình chữ nhật, \(AB = a\). Cạnh bên \(SA\) vuông góc với mặt phẳng \((ABCD)\) và \(SA = a\). Góc giữa đường thẳng \(SB\) và \(CD\) là:
Ta có AB // CD \( \Rightarrow \angle \left( {SB,CD} \right) = \angle \left( {SB,AB} \right) = \angle SBA\).
Do tam giác SAB vuông cân tại A nên \(\angle SBA = {45^0}\). Vậy \(\angle \left( {SB;CD} \right) = {45^0}\).
Chọn D.
Gieo một con súc sắc cân đối, đồng chất một lần. Xác suất để xuất hiện mặt chẵn?
Gieo một con súc sắc ta có \(n\left( \Omega \right) = 6\).
Gọi A là biến cố : ‘‘xuất hiện mặt chẵn’’ \( \Rightarrow A = \left\{ {2;4;6} \right\} \Rightarrow n\left( A \right) = 3\).
Vậy \(P\left( A \right) = \dfrac{3}{6} = \dfrac{1}{2}\).
Chọn A.
Số nghiệm nguyên của bất phương trình\(\sqrt {2\left( {{x^2} - 1} \right)} \le x + 1\) là.
ĐK : \({x^2} - 1 \ge 0 \Leftrightarrow \left[ \begin{array}{l}x \ge 1\\x \le - 1\end{array} \right.\).
\(\sqrt {2\left( {{x^2} - 1} \right)} \le x + 1 \Leftrightarrow \left\{ \begin{array}{l}x + 1 \ge 0\\2\left( {{x^2} - 1} \right) \le {x^2} + 2x + 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge - 1\\{x^2} - 2x - 3 \le 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge - 1\\ - 1 \le x \le 3\end{array} \right. \Leftrightarrow - 1 \le x \le 3\).
Kết hợp ĐK ta có \(\left[ \begin{array}{l}x = - 1\\1 \le x \le 3\end{array} \right.\). Vậy số nghiệm nguyên của phương trình là 4.
Chọn C.
Phương trình tiếp tuyến với đồ thị hàm số \(y = \dfrac{{x + 1}}{{x - 1}}\) song song với đường thẳng \(\left( \Delta \right):\,\,2x + y + 1 = 0\) là.
TXĐ: \(D = R\backslash \left\{ 1 \right\}\). Ta có \(y' = \dfrac{{ - 2}}{{{{\left( {x - 1} \right)}^2}}}\).
Phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ \(x = {x_0}\) là : \(y = \dfrac{{ - 2}}{{{{\left( {{x_0} - 1} \right)}^2}}}\left( {x - {x_0}} \right) + \dfrac{{{x_0} + 1}}{{{x_0} - 1}}\,\,\left( d \right)\)
Vì \(\left( d \right)//\Delta :\,\,2x + y + 1 = 0 \Leftrightarrow y = - 2x - 1 \Rightarrow \dfrac{{ - 2}}{{{{\left( {{x_0} - 1} \right)}^2}}} = - 2 \Leftrightarrow {\left( {{x_0} - 1} \right)^2} = 1 \Leftrightarrow \left[ \begin{array}{l}{x_0} = 2\\{x_0} = 0\end{array} \right.\).
Với \({x_0} = 2 \Rightarrow \left( d \right):\,\,y = - 2\left( {x - 2} \right) + 3 = - 2x + 7 \Leftrightarrow 2x + y - 7 = 0\).
Với \({x_0} = 0 \Rightarrow \left( d \right):\,\,y = - 2\left( {x - 0} \right) - 1 = - 2x - 1 \Leftrightarrow 2x + y + 1 = 0\,\,\left( {ktm\,\,do\,\,trung\,\,\Delta } \right)\).
Chọn A.
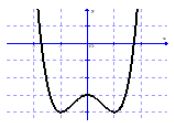
Đường cong trong hình vẽ bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi đó là hàm số nào?
+) Đồ thị hàm số đã cho là hàm bậc bốn trùng phương nên loại đáp án A và D.
+) \(\mathop {\lim }\limits_{x \to + \infty } y = + \infty \Rightarrow a > 0\), loại đáp án B.
Chọn C.
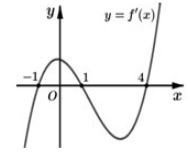
Cho hàm số \(f\left( x \right)\) xác định trên R và có đồ thị hàm số \(y = f'\left( x \right)\) là đường cong trong hình bên. Mệnh đề nào dưới đây đúng?
Dựa vào đồ thị hàm số \(y = f'\left( x \right)\) ta có \(\left\{ \begin{array}{l}f'\left( x \right) > 0 \Leftrightarrow x \in \left( { - 2;0} \right) \cup \left( {2; + \infty } \right)\\f'\left( x \right) > 0 \Leftrightarrow x \in \left( { - \infty ; - 2} \right) \cup \left( {0;2} \right)\end{array} \right.\) , do đó hàm số \(y = f\left( x \right)\) đồng biến trên \(\left( { - 2;0} \right)\) và \(\left( {2; + \infty } \right)\), nghịch biến trên \(\left( { - \infty ; - 2} \right)\) và \(\left( {0;2} \right)\).
Chọn D.
Một hộp đựng 11 tấm thẻ được đánh số từ 1 đến 11. Chọn ngẫu nhiên 6 tấm thẻ. Gọi \(P\) là xác suất để tổng số ghi trên 6 tấm thẻ ấy là một số lẻ. Khi đó \(P\) bằng.
Số phần tử của không gian mẫu là \(n\left( \Omega \right) = C_{11}^6 = 462\).
Gọi A là biến cố :"Tổng số ghi trên 6 tấm thẻ là số lẻ".
TH1: 5 thẻ mang số lẻ và 1 thẻ mang số chẵn \( \Rightarrow \) có \(C_6^5.C_5^1 = 30\) cách chọn.
TH2: 3 thẻ mang số lẻ và 3 thẻ mang số chẵn \( \Rightarrow \) có \(C_6^3.C_5^3 = 200\) cách chọn.
TH3: 1 thẻ mang số lẻ và 5 thẻ mang số chẵn \( \Rightarrow \) có \(C_6^1.C_5^5 = 6\) cách chọn.
\( \Rightarrow n\left( A \right) = 30 + 200 + 6 = 236\),
Vậy \(P\left( A \right) = \dfrac{{236}}{{462}} = \dfrac{{118}}{{231}}\).
Chọn C.
Điểm cực tiểu của hàm số \(y = {x^3} - 3{x^2} - 9x + 2\).
Ta có : \(f'\left( x \right) = 3{x^2} - 6x - 9;\,\,f''\left( x \right) = 6x - 6\).
Xét hệ \(\left\{ \begin{array}{l}f'\left( x \right) = 0\\f''\left( x \right) > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}3{x^2} - 6x - 9 = 0\\6x - 6 > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}x = 3\\x = - 1\end{array} \right.\\x > 1\end{array} \right. \Leftrightarrow x = 3\).
Vậy điểm cực tiểu của hàm số là \(x = 3\).
Chọn B.
Cho hàm số \(y = f(x)\) có bảng biến thiên như bên.
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
Dựa vào BBT của hàm số ta thấy hàm số đã cho nghịch biến trên \(\left( { - \infty ; - 1} \right)\) và \(\left( {0;1} \right)\). Có \(\left( { - \infty ; - 2} \right) \subset \left( { - \infty ; - 1} \right)\) do đó hàm số nghịch biến trên \(\left( { - \infty ; - 2} \right)\).
Chọn D.
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. SA\( \bot \)(ABCD) và \(SB = \sqrt 3 \). Thể tích khối chóp S.ABCD là.
Vì \(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot AB \Rightarrow \Delta SAB\) vuông tại A. Áp dụng định lí Pytago ta có : \(SA = \sqrt {S{B^2} - A{B^2}} = a\sqrt 2 \).
Vậy \({V_{S.ABCD}} = \dfrac{1}{3}SA.{S_{ABCD}} = \dfrac{1}{3}.a\sqrt 2 .{a^2} = \dfrac{{{a^3}\sqrt 2 }}{3}\).
Chọn D.
Phương trình tiếp tuyến của đồ thị hàm số \(y = {x^3} - 3{x^2} - x + 3\) tại điểm \(M\left( {1;0} \right)\) là.
Ta có \(y' = 3{x^2} - 6x - 1 \Rightarrow y'\left( 1 \right) = - 4\).
Vậy phương trình tiếp tuyến của đồ thị hàm số đã cho tại \(M\left( {1;0} \right)\) là \(y = - 4\left( {x - 1} \right) + 0 = - 4x + 4\).
Chọn C.
Giá trị lớn nhất của hàm số \(y = \dfrac{{{x^2} - 3x}}{{x + 1}}\) trên đoạn \(\left[ {0;3} \right]\) bằng.
ĐKXĐ: \(x \ne - 1\).
Ta có: \(y' = \dfrac{{\left( {2x - 3} \right)\left( {x + 1} \right) - \left( {{x^2} - 3x} \right)}}{{{{\left( {x + 1} \right)}^2}}} = \dfrac{{{x^2} + 2x - 3}}{{{{\left( {x + 1} \right)}^2}}} = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1 \in \left[ {0;3} \right]\\x = - 3 \notin \left[ {0;3} \right]\end{array} \right.\)
\(y\left( 1 \right) = - 1;\,\,y\left( 0 \right) = 0;\,\,y\left( 3 \right) = 0 \Rightarrow \mathop {\max }\limits_{\left[ {0;3} \right]} y = 0\).
Chọn C.
Cho hàm số \(y = f\left( x \right) = \dfrac{1}{3}{x^3} - \left( {m + 1} \right){x^2} + \left( {m + 3} \right)x + m - 4\). Tìm để hàm số \(y = f\left( {\left| x \right|} \right)\) có 5 điểm cực trị?
Đồ thị hàm số \(y = f\left( {\left| x \right|} \right)\) nhận đượcbằng cách như sau :
+) Vẽ đồ thị hàm số \(y = f\left( x \right)\).
+) Xóa phần đồ thì hàm số \(y = f\left( x \right)\) bên trái trục Oy.
+) Lấy đối xứng toàn bộ phần đồ thị hàm số \(y = f\left( x \right)\) bên phải trục Oy qua Oy.
Do đó hàm số \(y = f\left( {\left| x \right|} \right)\) có 5 điểm cực trị thì hàm số \(y = f\left( x \right)\) phải có 2 điểm cực trị phân biệt có hoành độ dương \( \Leftrightarrow \) phương trình \(f'\left( x \right) = 0\) có 2 nghiệm dương phân biệt.
Xét phương trình \(f'\left( x \right) = 0 \Leftrightarrow {x^2} - 2\left( {m + 1} \right)x + m + 3 = 0\) có 2 nghiệm dương phân biệt
\( \Leftrightarrow \left\{ \begin{array}{l}\Delta ' = {\left( {m + 1} \right)^2} - \left( {m + 3} \right) > 0\\S = 2\left( {m + 1} \right) > 0\\P = m + 3 > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{m^2} + m - 2 > 0\\m > - 1\\m > - 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}m > 1\\m < - 2\end{array} \right.\\m > - 1\end{array} \right. \Leftrightarrow m > 1\).
Chọn B.
Đồ thị hàm số \(y = \dfrac{{2x + 1}}{{x - 1}}\) có tiệm cận ngang là.
Đồ thị hàm số \(y = \dfrac{{2x + 1}}{{x - 1}}\) có tiệm cận ngang là \(y = 2\).
Chọn A.
Số cách xếp 5 người vào 5 vị trí ngồi thành hàng ngang là.
Xếp 5 người vào 5 vị trí ngồi thành hàng ngang có \(5! = 120\) cách.
Chọn A.
Biết \({m_0}\) là giá trị của tham số m để hàm số \(y = {x^3} - 3{x^2} + mx - 1\) có hai điểm cực trị \({x_1},\,\,{x_2}\) sao cho \(x_1^2 + x_2^2 - {x_1}{x_2} = 13\). Mệnh đề nào dưới đây đúng?
TXĐ : \(D = R\).
Ta có \(y' = 3{x^2} - 6x + m = 0\). Để hàm số có 2 điểm cực trị \({x_1},\,\,{x_2}\) thì phương trình \(y' = 0\) có 2 nghiệm phân biệt \( \Leftrightarrow \Delta ' = 9 - 3m > 0 \Leftrightarrow m < 3\).
Áp dụng định lí Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2\\{x_1}{x_2} = \dfrac{m}{3}\end{array} \right.\).
Theo giả thiết ta có : \(x_1^2 + x_2^2 - {x_1}{x_2} = 13 \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} - 3{x_1}{x_2} = 13 \Leftrightarrow 4 - m = 13 \Leftrightarrow m = - 9\) (tm).
Dựa vào các đáp án ta thấy \({m_0} = - 9 \in \left( { - 15; - 7} \right)\).
Chọn B.
Đồ thị sau đây là của hàm số nào?
Dựa vào đồ thị hàm số ta thấy đồ thị hàm số có TCN \(y = 1\) và TCĐ \(x = 2\).
Chọn B.
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình chữ nhật, \(AB = a,{\rm{ }}AD = 2a\), \(SA\) vuông góc với mặt phẳng\(\left( {ABCD} \right)\), \(SA = a\sqrt 3 \). Thể tích của khối chóp \(S.ABCD\) là.
\({V_{S.ABCD}} = \dfrac{1}{3}SA.{S_{ABCD}} = \dfrac{1}{3}SA.AB.AD = \dfrac{1}{3}.a\sqrt 3 .a.2a = \dfrac{{2{a^3}\sqrt 3 }}{3}\).
Chọn C.
Cho \(\sin \alpha = \dfrac{1}{3}\)và \(\dfrac{\pi }{2} < \alpha < \pi \). Khi đó \(\cos \alpha \) có giá trị là.
Ta có \({\sin ^2}\alpha + {\cos ^2}\alpha = 1 \Leftrightarrow {\cos ^2}\alpha = 1 - {\left( {\dfrac{1}{3}} \right)^2} = \dfrac{8}{9}\).
Do \(\dfrac{\pi }{2} < \alpha < \pi \Rightarrow \cos \alpha < 0 \Leftrightarrow \cos \alpha = \dfrac{{ - 2\sqrt 2 }}{3}\).
Chọn D.
\(\mathop {\lim }\limits_{x \to {1^ + }} \dfrac{{ - 2x + 1}}{{x - 1}}\) bằng.
Khi \(x \to {1^ + }\) Ta có \(\left\{ \begin{array}{l}\mathop {\lim }\limits_{x \to {1^ + }} \left( {x - 1} \right) = 0\\\mathop {\lim }\limits_{x \to {1^ + }} \left( { - 2x + 1} \right) = - 1\\x - 1 > 0\end{array} \right. \Rightarrow \mathop {\lim }\limits_{x \to {1^ + }} \dfrac{{ - 2x + 1}}{{x - 1}} = - \infty \).
Chọn B.
Người ta muốn xây một bể chứa nước dạng hình hộp chữ nhật không nắp có thể tích bằng \(200{m^3}\) đáy bể là hình chữ nhật có chiều dài gấp đôi chiều rộng. Giá thuê nhân công xây bể là 300.000 đồng/m2. Chi phí thuê nhân công thấp nhất là.
Gọi chiều rộng, chiều dài và chiều cao của bể lần lượt là x, 2x, h (\(x > 0,\,\,h > 0\)).
Khi đó thể tích của bể là \(V = 2{x^2}h = 200 \Rightarrow h = \dfrac{{100}}{{{x^2}}}\).
Diện tích xung quanh và diện tích dáy bể là \(S = 2xh + 2.2x.h + 2x.x = 6xh + 2{x^2}\)
\( \Rightarrow S = 6x.\dfrac{{100}}{{{x^2}}} + 2{x^2} = \dfrac{{600}}{x} + 2{x^2} = \dfrac{{300}}{x} + \dfrac{{300}}{x} + 2{x^2} \ge 3\sqrt[3]{{\dfrac{{300}}{x}.\dfrac{{300}}{x}.2{x^2}}} = 3\sqrt[3]{{180000}} = 30\sqrt[3]{{180}}\)
\( \Rightarrow {S_{\min }} = 30\sqrt[3]{{180}}\) . Dấu "=" xảy ra \( \Leftrightarrow \dfrac{{300}}{x} = 2{x^2} \Leftrightarrow x = \sqrt[3]{{150}}\).
Vậy chi phí thấp nhất để xây bể là \(30\sqrt[3]{{180}}.300\,\,000 \approx 50\,815\,945 \simeq 51\) triệu đồng.
Chọn A.
Có bao nhiêu giá trị nguyên m để đường thẳng \(\left( d \right):\,\,y = x - m\) cắt đồ thị hàm số \(y = \dfrac{{x + 1}}{{x - 1}}\) tại hai điểm phân biệt A, B sao cho \(AB = 3\sqrt 2 \).
Xét phương trình hoành độ giao điểm
\(x - m = \dfrac{{x + 1}}{{x - 1}}\,\,\left( {x \ne 1} \right) \Leftrightarrow \left( {x - m} \right)\left( {x - 1} \right) = x + 1 \Leftrightarrow {x^2} - \left( {2 + m} \right)x + m - 1 = 0\,\,\left( * \right)\).
Để đường thẳng thẳng \(\left( d \right):\,\,y = x - m\) cắt đồ thị hàm số \(y = \dfrac{{x + 1}}{{x - 1}}\) tại hai điểm phân biệt A, B thì phương trình (*) phải có 2 nghiệm phân biệt \( \Leftrightarrow \Delta > 0\).
\( \Leftrightarrow {\left( {2 + m} \right)^2} - 4\left( {m - 1} \right) > 0 \Leftrightarrow {m^2} + 8 > 0\) (luôn đúng).
Gọi \({x_A},\,\,{x_B}\) lần lượt là hoành độ của điểm A, B \( \Rightarrow \) \({x_A},\,\,{x_B}\) là 2 nghiệm phân biệt của phương trình (*). Áp dụng định lí Vi-ét ta có : \(\left\{ \begin{array}{l}{x_A} + {x_B} = 2 + m\\{x_A}{x_B} = m - 1\end{array} \right.\).
\(\begin{array}{l}A\left( {{x_A};\,\,{x_A} - m} \right);\,\,B\left( {{x_B};{x_B} - m} \right) \Rightarrow A{B^2} = {\left( {{x_B} - {x_A}} \right)^2} + {\left( {{x_B} - {x_A}} \right)^2} = 2{\left( {{x_B} - {x_A}} \right)^2} = 18\\ \Leftrightarrow {\left( {{x_A} + {x_B}} \right)^2} - 4{x_A}{x_B} = 9 \Leftrightarrow {\left( {2 + m} \right)^2} - 4\left( {m - 1} \right) = 9 \Leftrightarrow {m^2} + 8 = 9 \Leftrightarrow m = \pm 1\end{array}\)
Chọn C.
Cho hàm số \(y = f\left( x \right)\)có đồ thị như hình bên.
Tìm tất cả các giá trị thực của tham số \(m\) để phương trình \(f\left( x \right) = m + 2\) có bốn nghiệm phân biệt.
Số nghiệm của phương trình \(f\left( x \right) = m + 2\) là số giao điểm của đồ thị hàm số \(y = f\left( x \right)\) và đường thẳng \(y = m + 2\) song song với trục hoành.
Dựa vào đồ thị hàm số \(y = f\left( x \right)\) ta thấy để đường thẳng \(y = m + 2\) cắt đồ thị tại 4 điểm phân biệt \( \Leftrightarrow - 4 < m + 2 < - 3 \Leftrightarrow - 6 < m < - 5\).
Chọn D.
Gọi \(S\)là diện tích đáy, \(h\)là chiều cao. Thể tích khối lăng trụ là.
Thể tích khối lăng trụ có chiều cao h và bán kính đáy S là : \(V = Sh\).
Chọn C.
Cho hàm số \(f(x)\) có đạo hàm \(f'(x)\) có đồ thị như hình vẽ. Hàm số \(g(x) = f(x) - \dfrac{{{x^3}}}{3} + {x^2} - x + 2\) đạt cực đại tại điểm nào?
Ta có \(g'\left( x \right) = f'\left( x \right) - {x^2} + 2x - 1 = 0 \Leftrightarrow f'\left( x \right) = {x^2} - 2x + 1\).
Số nghiệm của phương trình là số giao điểm của đồ thị hàm số \(y = f'\left( x \right)\) và đồ thị hàm số \(y = {x^2} - 2x + 1\). Ta có hình ảnh đồ thị hàm số như sau :
Dựa vào đồ thị ta thấy phương trình \(f'\left( x \right) = {x^2} - 2x + 1\) có 3 nghiệm phân biệt.
Ta có bảng xét dấu \(g'\left( x \right)\) như sau :
Vậy hàm số \(y = g\left( x \right)\) đạt cực đại tại \(x = 1\).
Chọn C.
Trong mặt phẳng với hệ toạ độ Oxy, cho tam giác ABC có đỉnh \(B( - 12;1)\), đường phân giác trong góc A có phương trình \(d:x + 2y - 5 = 0\). \(G\left( {\dfrac{1}{3};\dfrac{2}{3}} \right)\) là trọng tâm tam giác ABC. Đường thẳng BC qua điểm nào sau đây.
Gọi M là trung điểm của AC, ta có \(\overrightarrow {BG} = 2\overrightarrow {GM} \Rightarrow \left\{ \begin{array}{l}\dfrac{{37}}{3} = 2\left( {{x_M} - \dfrac{1}{3}} \right)\\\dfrac{{ - 1}}{3} = 2\left( {{y_M} - \dfrac{2}{3}} \right)\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_M} = \dfrac{{13}}{2}\\{y_M} = \dfrac{1}{2}\end{array} \right. \Rightarrow M\left( {\dfrac{{13}}{2};\dfrac{1}{2}} \right)\).
Gọi B’ là điểm đối xứng với B qua đường thẳng \(\left( d \right):\,\,x + 2y - 5 = 0 \Rightarrow B' \in AC\).
Gọi d’ là đường thẳng qua B và vuông góc với (d) \( \Rightarrow \) Phương trình (d’) : \(2x - y + 25 = 0\).
Gọi \(H = \left( {d'} \right) \cap \left( d \right) \Rightarrow H\left( { - 9;7} \right)\) là trung điểm của BB’ \( \Rightarrow B'\left( { - 6;13} \right)\).
Phương trình đường thẳng AC đi qua hai điểm B’, M là \(\dfrac{{x - \dfrac{{13}}{2}}}{{ - 6 - \dfrac{{13}}{2}}} = \dfrac{{y - \dfrac{1}{2}}}{{13 - \dfrac{1}{2}}} \Leftrightarrow \dfrac{{25}}{2}\left( {x - \dfrac{{13}}{2}} \right) = \dfrac{{ - 25}}{2}\left( {y - \dfrac{1}{2}} \right) \Leftrightarrow x - \dfrac{{13}}{2} = - y + \dfrac{1}{2} \Leftrightarrow x + y - 7 = 0\).
\(A = d \cap AC \Rightarrow A\left( {9; - 2} \right)\). M là trung điểm của AC \( \Rightarrow C\left( {4;3} \right)\).
\( \Rightarrow \) Phương trình đường thẳng BC là \(\dfrac{{x + 12}}{{4 + 12}} = \dfrac{{y - 1}}{{3 - 1}} \Leftrightarrow x - 8y + 20 = 0\).
Dựa vào các đáp án ta thấy BC đi qua điểm \(\left( {4;3} \right)\).
Chọn D.
Đồ thị sau đây là của hàm số nào ?
Đồ thị hàm số đã cho là đồ thị hàm đa thức bậc ba có dạng \(y = a{x^3} + b{x^2} + c\,\,\left( {a \ne 0} \right)\).
Ta có : \(\mathop {\lim }\limits_{x \to + \infty } y = - \infty \Rightarrow a < 0 \Rightarrow \) Loại đáp án B và D.
Xét đáp án A có \(y' = - 3{x^2} - 6x = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = - 2\end{array} \right.\) , do đó loại đáp án A.
Chọn C.
Cho hình chóp tam giác \(S.ABC\)với \(ABC\)là tam giác đều cạnh \(a\). \(SA \bot (ABC)\) và \(SA = a\sqrt 3 .\) Tính thể tích của khối chóp \(S.ABC\).
Do tam giác ABC đều cạnh a nên ta có \({S_{\Delta ABC}} = \dfrac{{{a^2}\sqrt 3 }}{4}\).
Vậy \({V_{S.ABC}} = \dfrac{1}{3}SA.{S_{\Delta ABC}} = \dfrac{1}{3}.a\sqrt 3 .\dfrac{{{a^2}\sqrt 3 }}{4} = \dfrac{{{a^3}}}{4}\).
Chọn C.
Hỏi có tất cả bao nhiêu giá trị nguyên của m để đồ thị hàm số \(y = 2{x^3} - 3\left( {m + 3} \right){x^2} + 18mx - 8\) tiếp xúc với trục hoành?
Ta có : \(y' = 6{x^2} - 6\left( {m + 3} \right)x + 18m\).
Để đồ thị hàm số đã cho tiếp xúc với trục hoành thì hệ phương trình \(\left\{ \begin{array}{l}2{x^3} - 3\left( {m + 3} \right){x^2} + 18mx - 8 = 0\,\,\,\left( 1 \right)\\6{x^2} - 6\left( {m + 3} \right) + 18m = 0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 2 \right)\end{array} \right.\) có nghiệm.
\(\left( 2 \right) \Leftrightarrow {x^2} - \left( {m + 3} \right)x + 3m = 0\) có \(\Delta = {\left( {m + 3} \right)^2} - 12m = {\left( {m - 3} \right)^2}\), do đó phương trình (2) có 2 nghiệm \(\left[ \begin{array}{l}x = m\\x = 3\end{array} \right.\)
+) Với \(x = 3\) ta có: \(\left( 1 \right) \Leftrightarrow 54 - 27\left( {m + 3} \right) + 54m - 8 = 0 \Leftrightarrow m = \dfrac{{35}}{{27}}\).
+) Với \(x = m\) ta có: \(\left( 1 \right) \Leftrightarrow 2{m^3} - 3{m^3} - 9{m^2} + 18{m^2} - 8 = 0 \Leftrightarrow - 3{m^3} + 9{m^2} - 8 = 0 \Leftrightarrow \left[ \begin{array}{l}m = 1\\m = 4 \pm 2\sqrt 6 \end{array} \right.\).
Vậy chỉ có 1 giá trị nguyên của m thỏa mãn yêu cầu bài toán là \(m = 1\).
Chọn B.
Gọi\(S\) là tập hợp các số nguyên \(m\) để hàm số \(y = f(x) = \dfrac{{x + 2m - 3}}{{x - 3m + 2}}\) đồng biến trên khoảng \(\left( { - \infty ; - 14} \right)\). Tính tổng \(T\) của các phần tử trong \(S\)?
TXĐ : \(D = R\backslash \left\{ {3m - 2} \right\}\).
Ta có: \(y' = \dfrac{{ - 3m + 2 - 2m + 3}}{{{{\left( {x - 3m + 2} \right)}^2}}} = \dfrac{{ - 5m + 5}}{{{{\left( {x - 3m + 2} \right)}^2}}}\).
Để hàm số đã cho đồng biến trên \(\left( { - \infty ; - 14} \right) \Leftrightarrow \left\{ \begin{array}{l} - 5m + 5 > 0\\3m - 2 \ge - 14\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m < 1\\m \ge - 4\end{array} \right. \Leftrightarrow - 4 \le m < 1\).
\( \Rightarrow S = \left\{ { - 4; - 3; - 2; - 1;0} \right\} \Rightarrow \) Tổng các phần tử của S bằng -10.
Chọn A.
Cho khối chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(2a\). Hình chiếu vuông góc của \(S\) trên mặt phẳng\(\left( {ABCD} \right)\) là điểm \(H\) thuộc đoạn \(BD\) sao cho\(HD = 3HB\). Biết góc giữa mặt phẳng \(\left( {SCD} \right)\) và mặt phẳng đáy bằng\({45^0}\). Khoảng cách giữa hai đường thẳng \(SA\) và \(BD\) là.
Kẻ \(HM//BC \Rightarrow HM \bot CD \Rightarrow \angle \left( {\left( {SCD} \right);\left( {ABCD} \right)} \right) = \angle SMH = {45^0}\).
Kẻ \(AE//BD\,\,\left( {E \in BC} \right)\) \( \Rightarrow BD//\left( {SAE} \right) \Rightarrow d\left( {SA;BD} \right) = d\left( {BD;\left( {SAE} \right)} \right) = d\left( {H;\left( {SAE} \right)} \right)\).
Trong (ABCD) kẻ \(HI//AC\,\,\left( {I \in AE} \right)\). Vì \(AC \bot BD \Rightarrow HI \bot AE\).
Trong (SHI) kẻ \(HK \bot SI\) ta có:
\(\left\{ \begin{array}{l}AE \bot IH\\AE \bot SH\end{array} \right. \Rightarrow AE \bot \left( {SHI} \right) \Rightarrow AE \bot HK \Rightarrow HK \bot \left( {SAE} \right) \Rightarrow d\left( {H;\left( {SAE} \right)} \right) = HK\).
Gọi \(O = AC \cap BD\), dễ dàng chứng minh được OAIH là hình chữ nhật \( \Rightarrow HI = OA = \dfrac{{2a\sqrt 2 }}{2} = a\sqrt 2 \).
Áp dụng định lí Ta-lét ta có : \(\dfrac{{HM}}{{BC}} = \dfrac{{HD}}{{BD}} = \dfrac{3}{4} \Rightarrow HM = \dfrac{3}{4}BC = \dfrac{3}{4}.2a = \dfrac{{3a}}{2}\)
\( \Rightarrow SH = HM\tan {45^0} = \dfrac{{3a}}{2}\).
Áp dụng hệ thức lượng trong tam giác vuông SHI có : \(HK = \dfrac{{SH.HI}}{{\sqrt {S{H^2} + H{I^2}} }} = \dfrac{{\dfrac{{3a}}{2}.a\sqrt 2 }}{{\sqrt {\dfrac{{9{a^2}}}{4} + 2{a^2}} }} = \dfrac{{3a\sqrt {34} }}{{17}}\).
Chọn D.
Hàm số \(y = \dfrac{{2x - 1}}{{x + 1}}\). Khẳng định nào sau đây đúng.
TXĐ : \(D = R\backslash \left\{ 1 \right\}\).
Ta có \(y = \dfrac{{2.1 - 1.1}}{{{{\left( {x + 1} \right)}^2}}} = \dfrac{1}{{{{\left( {x + 1} \right)}^2}}} > 0\,\,\forall x \in D \Rightarrow \) Hàm số đã cho đồng biến trên \(\left( { - \infty ; - 1} \right)\) và \(\left( { - 1; + \infty } \right)\).
Chọn B.
Thể tích khối lăng trụ tam giác đều có tất cả các cạnh bằng a là.
Do đáy là tam giác đều cạnh a nên \({S_{day}} = \dfrac{{{a^2}\sqrt 3 }}{4}\). Chiều cao của lăng trụ là \(h = a\).
\( \Rightarrow {V_{lang\,\,tru}} = {S_{day}}.h = \dfrac{{{a^2}\sqrt 3 }}{4}.a = \dfrac{{{a^3}\sqrt 3 }}{4}\).
Chọn B.
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(a\), cạnh bên \(SA\) vuông góc với đáy \(\left( {ABCD} \right)\). Biết góc tạo bởi hai mặt phẳng \(\left( {SBC} \right)\) và \(\left( {ABCD} \right)\) bằng \(60^\circ \). Tính thể tích \(V\) của khối chóp \(S.ABCD\).
Ta có: \(\left\{ \begin{array}{l}BC \bot AB\\BC \bot SA\end{array} \right. \Rightarrow BC \bot \left( {SAB} \right) \Rightarrow BC \bot SB\)
\(\left\{ \begin{array}{l}\left( {SBC} \right) \cap \left( {ABCD} \right) = BC\\\left( {SBC} \right) \supset SB \bot BC\\\left( {ABCD} \right) \supset AB \bot BC\end{array} \right. \Rightarrow \angle \left( {\left( {SBC} \right);\left( {ABCD} \right)} \right) = \angle \left( {SB;AB} \right) = \angle SBA = {60^0}\)
Ta có: \(SA = AB\tan 60 = a\sqrt 3 \)\( \Rightarrow {V_{S.ABCD}} = \dfrac{1}{3}SA.{S_{ABCD}} = \dfrac{1}{3}.a\sqrt 3 .{a^2} = \dfrac{{{a^3}\sqrt 3 }}{3}\).
Chọn B.
Giá trị cực tiểu của hàm số \(y = {x^4} - 2{x^2} - 3\)là.
Ta có \(y' = 4{x^3} - 4x,\,\,y'' = 12{x^2} - 4\).
Xét hệ \(\left\{ \begin{array}{l}4{x^3} - 4x = 0\\12{x^2} - 4 > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}x = 0\\x = \pm 1\end{array} \right.\\\left[ \begin{array}{l}x > \dfrac{1}{{\sqrt 3 }}\\x < - \dfrac{1}{{\sqrt 3 }}\end{array} \right.\end{array} \right. \Leftrightarrow x = \pm 1\). Do đó hàm số đã cho đạt cực tiểu tại hai điểm \(x = \pm 1\). Khi đó ta có \({y_{CT}} = y\left( { - 1} \right) = y\left( 1 \right) = - 4\).
Chọn D.
Phương trình \(\cos x = \cos \dfrac{\pi }{3}\) có nghiệm là:
\(\cos x = \cos \dfrac{\pi }{3} \Leftrightarrow x = \pm \dfrac{\pi }{3} + k2\pi \,\,\left( {k \in Z} \right)\).
Chọn C.
Hàm số \(y = - {x^3} - 3{x^2} + 9x + 20\) đồng biến trên các khoảng.
TXĐ: \(D = R\). Ta có \(y' = - 3{x^2} - 6x + 9 > 0 \Leftrightarrow - 3 < x < 1 \Rightarrow \) Hàm số đồng biến trên \(\left( { - 3;1} \right)\).
Chọn A.
Khoảng cách từ \(I(1; - 2)\) đến đường thẳng \(\Delta :3x - 4y - 26 = 0\) bằng.
Ta có: \(d\left( {I;\Delta } \right) = \dfrac{{\left| {3.1 - 4\left( { - 2} \right) - 26} \right|}}{{\sqrt {{3^2} + {4^2}} }} = \dfrac{{15}}{5} = 3\).
Chọn A.
Để giá trị lớn nhất của hàm số \(y = \left| {\sqrt {2x - {x^2}} - 3m + 4} \right|\) đạt giá trị nhỏ nhất thì m thỏa.
Đặt \(t = \sqrt {2x - {x^2}} = \sqrt {1 - \left( {1 - 2x + {x^2}} \right)} = \sqrt {1 - {{\left( {x - 1} \right)}^2}} \Rightarrow t \in \left[ {0;1} \right]\).
Khi đó hàm số đã cho trở thành \(y = \left| {t - 3m + 4} \right|\) với \(t \in \left[ {0;1} \right]\).
Khi đó ta có
\(\max y = \max \left\{ {\left| { - 3m + 4} \right|;\left| {5 - 4m} \right|} \right\} \ge \dfrac{{\left| { - 3m + 4} \right| + \left| {5 - 3m} \right|}}{2} = \dfrac{{\left| {3m - 4} \right| + \left| {5 - 3m} \right|}}{2} \ge \dfrac{{\left| {3m - 4 + 5 - 3m} \right|}}{2} = \dfrac{1}{2}\)
Dấu "=" xảy ra \( \Leftrightarrow \left\{ \begin{array}{l}3m - 4 = 5 - 3m\\\left( {3m - 4} \right)\left( {5 - 3m} \right) \ge 0\end{array} \right. \Leftrightarrow m = \dfrac{3}{2}\).
Chọn A.
Cho hàm số \(y = f\left( x \right)\)liên tục trên đoạn \(\left[ { - 1;4} \right]\) và có đồ thị hàm số \(y = f'\left( x \right)\) như hình bên. Hỏi hàm số \(g\left( x \right) = f\left( {{x^2} + 1} \right)\) nghịch biến trên khoảng nào trong các khoảng sau?
Ta có \(g'\left( x \right) = 2xf'\left( {{x^2} + 1} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\{x^2} + 1 = - 1\\{x^2} + 1 = 1\\{x^2} + 1 = 4\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = \pm \sqrt 3 \end{array} \right.\).
Các nghiệm trên đều là các nghiệm bội lẻ, do đó đều là cực trị của hàm số \(y = g'\left( x \right)\).
Xét \(x = - 1\) ta có \(g'\left( { - 1} \right) = - 2f'\left( 2 \right) > 0\), từ đó ta có bảng xét dấu \(g'\left( x \right)\) như sau :
Dựa vào các đáp án ta thấy hàm số \(y = g\left( x \right)\) nghịch biến trên \(\left( {0;1} \right)\).
Chọn B.
Tính thể tích \(V\;\)của khối chóp có đáy là hình vuông cạnh \(2a\) và chiều cao là \(3a\)
Ta có diện tích đáy của hình chóp là: \(S = {\left( {2a} \right)^2} = 4{a^2}.\)
\( \Rightarrow V = \dfrac{1}{3}{S_d}.h = \dfrac{1}{3}.4{a^2}.3a = 4{a^3}.\)
Chọn A.

.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)

.JPG)
.JPG)
.JPG)