Cho hình chóp \(S . A B C D\) có đáy là hình thoi cạnh a ,\(\widehat{ B A D}=60^{\circ},S B=S D=S C\) , M là trung điểm của SD , H là hình chiếu của S trên mặt phẳng (ABCD). Tính khoảng cách giữa hai đường thẳng SH và CM
A. \(\frac{a \sqrt{17}}{14}\)
B. \(\frac{a \sqrt{3}}{14}\)
C. \(\frac{a \sqrt{7}}{7}\)
D. \(\frac{a \sqrt{3}}{7}\)
Lời giải của giáo viên
 HocOn247.com
HocOn247.com
Ta có ABCD là hình thoi có \(\widehat{B A D}=60^{\circ}\) nên tam giác BDC đều cạnh a.
Có \(\left\{\begin{array}{l} S B=S C=S D \\ S H \perp(A B C D) \end{array} \Rightarrow H\right.\) là trọng tâm tam giác BCD.
Gọi I ,N lần lượt là trung điểm của DH, BC.
\(\triangle S D H \text { có } M I\) là đường trung bình
\(\Rightarrow M I / / S H \Rightarrow S H / /(M I C) \Rightarrow d(S H, C M)=d(S H,(M C I))=d(H,(C M I))=H K\)
H K là đường cao của \(\Delta I H C\)
Ta có: \(S_{\Delta H C}=\frac{1}{2} \cdot I H \cdot C N=\frac{1}{2} \cdot \frac{1}{3} \cdot D N \cdot C N=\frac{1}{6} \cdot \frac{a \sqrt{3}}{2} \cdot \frac{a}{2}=\frac{a^{2} \sqrt{3}}{24}\)
\(\begin{array}{l} S_{\Delta H C}=\frac{1}{2} \cdot H K \cdot C I \Rightarrow H K=\frac{2 S_{\triangle H C}}{C I} \\ \Delta D I C \text { có: } I C=\sqrt{D I^{2}+D C^{2}-2 \cdot D I \cdot D C \cdot \cos 30^{\circ}}=\frac{\sqrt{7}}{\sqrt{12}} a \end{array}\)
Vậy \(H K=\frac{2 \mathrm{S}_{\mathrm{NHC}}}{I C}=\frac{2 \mathrm{a}^{2} \sqrt{3}}{24} \cdot \sqrt{\frac{7}{12}} \cdot a=\frac{a \sqrt{7}}{14}\)
CÂU HỎI CÙNG CHỦ ĐỀ
Cho x, y, zlà các số thực không âm thoả mãn \(12^{x}+2^{y}+2^{z}=10\) . Giá trị lớn nhất của biểu thức \(P=x+y+3 z\)gần nhất với số nào sau đây?
Gọi Alà tập các số tự nhiên có 5 chữ số đôi một khác nhau được lập từ các số 1;2;3;4;5;6;7;8;9. Lấy ngẫu nhiên một số thuộc tập A. Tính xác suất để số lấy được luôn có mặt hai chữ số 1;2 và chúng không đứng cạnh nhau
Trong không gian Oxyz , cho đường thẳng \(d: \frac{x-1}{2}=\frac{y+1}{1}=\frac{z-1}{2}\). Véc tơ nào sau đâu là véc tơ chỉ phương của đường thẳng d
Trong không gian Oxyz , mặt phẳng đi qua điểm M (1;2;3) và song song với mặt phẳng \((P): x-2 y+z-3=0\) có phương trình là
Cho lăng trụ tam giác đều \(A B C \cdot A^{\prime} B^{\prime} C^{\prime}\) có độ dài cạnh đáy bằng a, góc giữa đường thẳng AB' và mặt phẳng (ABC) bằng \(60^{\circ} .\) . Tính thể tích V của khối trụ ngoại tiếp lăng trụ đã cho
Tính thể tích V của khối chóp có đáy là hình vuông cạnh bằng 3 và chiều cao bằng 4
Trong không gian Oxyz cho mặt cầu (S) có tâm là I (0;0;1) và tiếp xúc với mặt phẳng \((\alpha): 2 x-2 y+z+8=0\) . Phương trình của (S ) là
Tất cả các giá trị của m để hàm số \(y=\frac{2 \cos x-1}{\cos x-m}\) đồng biến trên khoảng \(\left(0 ; \frac{\pi}{2}\right)\) là
Trên mặt phẳng tọa độ, điểm biểu diễn số phức liên hợp của số phức \(z=3+4 i\) là điểm nào dưới dây?
Trong không gian Oxyz , phương trình mặt phẳng trung trực của đoạn thẳng AB với \(A(3 ;-2 ; 1) \text { và } B(1 ; 0 ; 5)\) là:
Tổng số đường tiệm cận ngang của đồ thị hàm số \(y=\frac{2 x-1}{x+1}\)
Trong không gian Oxyz , cho điểm \(A(1 ;-3 ; 2)\) Tọa độ điểm A' đối xứng với A điểm qua mặt phẳng (Oyz) là
Cho hình chóp S. ABC có \(S A=S B\,\, và \,\,C A=C B\) . Góc giữa hai đường thẳng SC và AB bằng
Cho Hàm số f(x) liên tục trên \(\mathbb{R}\) và có đồ thị hàm số y =f'(x)như hình vẽ bên dưới
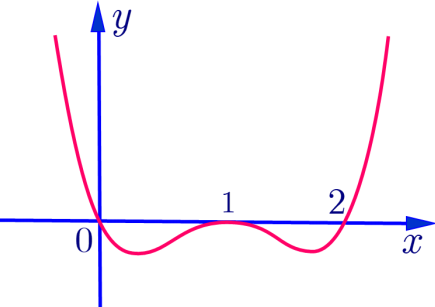
Hàm số \(g(x)=f\left(\frac{5 x}{x^{2}+4}\right)\) có bao nhiêu điểm cực đại?
Tính diện tích xung quanh của hình nón có bán kính đáy \(r=\sqrt{3}\) và chiều cao h = 4




