Lời giải của giáo viên
 HocOn247.com
HocOn247.com
Hình trụ có thiết diện qua trục là hình vuông cạnh 2a nên có đường sinh 2a và bán kính đáy a nên có diện tích toàn phần:
\(S_{t p}=2\pi Rl+2 \pi R^2=6 \pi a^{2}\)
CÂU HỎI CÙNG CHỦ ĐỀ
Cho hàm số y=f(x) liên tục trên \(\mathbb{R}\) và có bảng biến thiên như hình vẽ:
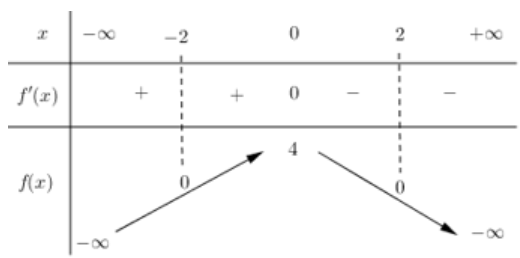
Có bao nhiêu giá trị nguyên của m để phương trình \(f( \sqrt{1+x}-\sqrt{3-x})=f( \sqrt{|m|+1})\) có nghiệm?
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, \(S A \perp(A B C D) \text { và } S A=a \sqrt{3}\) . Khi đó thể tích của hình chóp S.ABCD bằng:
Xét tích phân \(\int_{1}^{e} \frac{1}{x} \ln x d x . \text { Nếu đặt } \ln x=t \text { thì } \int_{1}^{e} \frac{1}{x} \ln x d x\) bằng:
Diện tích S của hình phẳng giới hạn bởi các đường \(y=4 x^{2}+x, y=-1, x=0 \text { và } x=1\) được tính bởi công thức nào sau đây?
Số tiệm cận của đồ thị hàm số \(y=\frac{2 x-3}{x+1}\)là:
Cho cấp số nhân với \(u_1=3\) và \(u_2 = 9\) . Công bội của cấp số nhân đã cho là:
Có bao nhiêu cặp số nguyên dương \((x ; y)\, với \,x \leq 2020\) thỏa mãn điều kiện \(\log _{2} \frac{x+2}{y+1}+x^{2}+4 x=4 y^{2}+8 y+1\).
Cho hình lập phương ABCD. A' B' C' D' cạnh bằng 3a ,\(K \in C C^{\prime} \text { sao cho } C K=\frac{2}{3} C C^{\prime}\). Mặt phẳng \((\alpha)\) qua A,K và song song với \(B'D'\) chia khối lập phương trình hai phần. Tính thể tích phần khối đa diện chứa đỉnh C.
Trong không gian Oxyz , Cho mặt cầu \((S): x^{2}+y^{2}+z^{2}+2 x+2 y-4 z-3=0\). Đường kính của (S) là:
Cho hàm số y=f(x) có bảng biến thiên như hình vẽ. Mệnh đề nào sau đây là sai?
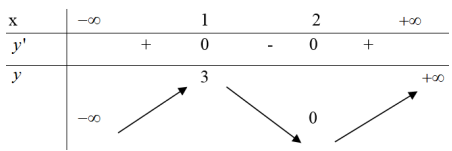
Giá trị nhỏ nhất của hàm số \(f(x)=x^{4}-6 x^{2}-9\) trên đoạn [-1;4] bằng:
Xét các số thực a, b thỏa mãn: \(\log _{8}\left(4^{a} . 8^{b}\right)=\log _{4} 16\). Mệnh đề nào dưới đây là đúng?
Số giao điểm của đồ thị hàm số \(y=-x^{3}+3 x^{2}-7\) và trục hoành là:
Trong không gian Oxyz, cho điểm \( M(1 ; 2 ; 3) ; N(-1 ; 1 ; 2)\) Phương trình mặt phẳng trung trực của MN là:




