Một con lắc lò xo được treo trên trần một thang máy. Khi thang máy đứng yên thì con lắc được kích thích dao động điều hòa theo phương thẳng đứng với chu kỳ 0,4 s, biên độ 5 cm. Vừa lúc quả cầu của con lắc đang đi qua vị trí lò xo không biến dạng theo chiều từ trên xuống thì thang máy chuyển động nhanh dần đều đi lên với gia tốc có độ lớn \(5\,\,{m}/{{{s}^{2}}}\;\). Lấy \(g={{\pi }^{2}}=10\,\,{m}/{{{s}^{2}}}\;\). Sau đó con lắc dao động với biên độ là
A. 7 cm.
B. \(3\sqrt{5}\,\,cm.\)
C. \(5\sqrt{3}\,\,cm.\)
D. \(5\,\,cm.\)
Lời giải của giáo viên
 HocOn247.com
HocOn247.com
Ta có độ biến dạng của lò xo tại vị trí cân bằng: \(\text{x}=\Delta \ell =\frac{mg}{k}=\frac{{{T}^{2}}g}{4{{\pi }^{2}}}=4\,\,cm.\)
Xét chuyển động của con lắc với thang máy: Chọn chiều dương hướng lên. Thang máy chuyển động nhanh dần đều ở vị trí: \(\text{x}=\Delta \ell \).
Khi thang máy chuyển động, vị trí cân bằng bị dịch xuống dưới một đoạn bằng:
\(y=\Delta \ell '=\frac{m\left( g+a \right)}{k}-\frac{mg}{k}=\frac{a}{{{\omega }^{2}}}=\frac{5}{{{\left( 5\pi \right)}^{2}}}=0,02\,m=2\,cm\)
Nên li độ lúc sau là: \(\text{x}'=x+y.\)
Ta có: \(A{{'}^{2}}=x{{'}^{2}}+{{\left( \frac{v}{\omega } \right)}^{2}}={{\left( x+y \right)}^{2}}+{{\left( \frac{v}{\omega } \right)}^{2}}\)
Từ đó ta có: \(A{{'}^{2}}={{x}^{2}}+2\text{x}y+{{y}^{2}}+{{\left( \frac{v}{\omega } \right)}^{2}}={{A}^{2}}+{{y}^{2}}+2\text{x}y\) .
Thay số vào ta được: \(A{{'}^{2}}={{5}^{2}}+{{2}^{2}}+2.4.2=45\Rightarrow A'=\sqrt{45}=3\sqrt{5}\,\,cm\)
CÂU HỎI CÙNG CHỦ ĐỀ
Xét một lượng chất phóng xạ xác định ban đầu khối lượng là m0 . Sau 1 năm, khối lượng chất phóng xạ giảm đi 3 lần. Hỏi sau 2 năm, khối lượng chất phóng xạ trên giảm đi bao nhiêu lần so với ban đầu.
Khi quan sát bong bóng xà phòng hay đĩa CD thì thấy lấp lánh, nhiều màu sặc sỡ là do hiện tượng
Cho ba vật dao động điểu hòa cùng biên độ \(A=10\,\,cm\) nhưng tần số khác nhau. Biết rằng tại mọi thời điểm li độ, vận tốc của các vật liên hệ với nhau bởi biểu thức \(\frac{{{x}_{1}}}{{{v}_{1}}}+\frac{{{x}_{2}}}{{{v}_{2}}}=\frac{{{x}_{3}}}{{{v}_{3}}}+2018\). Tại thời điểm t, các vật cách vị trí cân bằng của chúng lần lượt là 6 cm, 8 cm và \({{\text{x}}_{3}}\) . Giá trị \({{\text{x}}_{3}}\) gần giá trị nào nhất:
Gọi k là hệ số nhân nơtrôn thì điều kiện để phản ứng dây chuyền xảy ra là:
Quang điện trở có nguyên tắc hoạt động dựa trên hiện tượng
Công thoát của electron khỏi một kim loại là 6,625.10- 19J. Biết h = 6,625.10-34Js; c = 3.108m/s. Giới hạn quang điện của kim loại này là
Một máy phát điện xoay chiều một pha có phần cảm là rôto gồm 5 cặp cực (5 cực nam và 5 cực bắc). Để suất điện động do máy này sinh ra có tần số 50 Hz thì rôto phải quay với tốc độ.
Đặt một điện áp xoay chiều \(u=U\sqrt{2}\cos \left( \omega t \right)\,\left( V \right)\) vào hai đầu mạch điện AB mắc nối tiếp theo thứ tự gồm điện trở R, cuộn dây không thuần cảm (L, r) và tụ điện C với R = r. Gọi N là điểm nằm giữa điện trở R và cuộn dây, M là điểm nằm giữa cuộn dây và tụ điện. Điện áp tức thời \({{u}_{AM}}\) và \({{u}_{NB}}\) vuông pha với nhau và có cùng một giá trị hiệu dụng là \(30\sqrt{5}\,V\). Giá trị của U bằng:
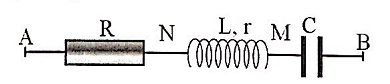
Bắn một hạt nơtron có động năng 2 MeV vào hạt nhân \({}_{3}^{6}Li\) đang đứng yên thì thu được hạt anpha và hạt nhân X có hướng chuyển động hợp với hướng tới của hạt nơtron các góc lần lượt là 25° và 30°. Phản ứng này tỏa hay thu bao nhiêu năng lượng?
Trong nguyên tử hidro, khi êlêctrôn chuyển động trên quỹ đạo K với bán kính \({{r}_{0}}={{5,3.10}^{-11}}m\) thì tốc độ của electron chuyển động trên quỹ đạo đó là
Điện áp giữa hai đầu một đoạn mạch có giá trị cực đại là 220V. Giá trị hiệu dụng của điện áp này là
Một tàu phá băng công suất 16 MW. Tàu dùng năng lượng phân hạch của hạt nhân \(^{235}U\). Trung bình mỗi phân hạch tỏa ra 200 MeV. Nhiên liệu dùng trong lò là \(^{235}U\) làm giàu đến 12,5% (tính theo khối lượng). Hiệu suất của lò là 30 %. Hỏi nếu tàu làm việc liên tục trong 3 tháng thì cần bao nhiêu kg nhiên liệu (coi mỗi ngày làm việc 24 giờ, 1 tháng tính 30 ngày)
Trong phản ứng hạt nhân \({}_{2}^{4}He+{}_{13}^{27}Al\to {}_{15}^{30}P+X\) hạt X là.

