Đề thi thử THPT QG năm 2021 môn Vật Lý - Trường THPT Lạng Giang
Đề thi thử THPT QG năm 2021 môn Vật Lý
-
Hocon247
-
40 câu hỏi
-
90 phút
-
56 lượt thi
-
Trung bình
Tham gia [ Hs Hocon247.com ] - Cộng Đồng Luyện Thi Trực Tuyến để được học tập những kiến thức bổ ích từ HocOn247.com
Một vật dao động tắt dần có các đại lượng nào sau đây giảm liên tục theo thời gian?
Trong dao động tắt dần, hai đại lượng giảm liên tục theo thời gian là: Biên độ và cơ năng.
Một vật m = 200g dao động điều hòa. Trong khoảng thời gian một chu kì vật đi được một đoạn 40cm. Tại vị trí x = 5cm thì động năng của vật là 0,375J. Chu kì dao động:
Chu kì dao động 0,28s
Một sóng cơ có tần số 0,5 Hz truyền trên một sợi dây đàn hồi đủ dài với tốc độ 0,5 m/s. Sóng này có bước sóng là
Sóng này có bước sóng là 1 m
Một sóng dọc truyền trong một môi trường thì phương dao động của các phần tử môi trường
Sóng dọc là sóng có phương dao động trùng với phương truyền sóng.
Một sóng cơ truyền dọc theo trục Ox có phương trình u = Acos(20πt – πx) (cm), với t tính băng s. Tần số của sóng này bằng
Tần số : \(\omega =2\pi f\Rightarrow f=\frac{\omega }{2\pi }=10(Hz)\)
Tại một điểm trên mặt chất lỏng có một nguồn dao động với tần số 120Hz, tạo ra sóng ổn định trên mặt chất lỏng. Xét 5 gợn lồi liên tiếp trên một phương truyền sóng, ở về một phía so với nguồn, gợn thứ nhất cách gợn thứ năm 0,5m. Tốc độ truyền sóng là
Theo đề 5 gợn liên tiếp: => 4λ = 0,5 m => λ = 0,125 m.
Vậy v = λf = 15 m/s.
Một mạch dao động điện từ lý tưởng gồm cuộn cảm thuần có độ tự cảm L và tụ điện có điện dung C. Chu kì dao đông riêng của mạch là
Công thức xác định chu kì dao động của mạch dao động là \(T=2\pi \sqrt{LC}\)
Mạch dao độngLC gồm tụ C = 6(µF) và cuộn cảm thuần . Biết giá trị cực đại của điện áp giữa hai đầu của tụ điện là U0 =14V. Tại thời điểm điện áp giữa hai bản tụ là u=8V, năng lượng từ trường trong mạch bằng
Bảo toàn năng lượng và thay số ta được năng lượng từ trường trong mạch là: 396 µJ
Điện áp giữa hai đầu một đoạn mạch có giá trị cực đại là 220V. Giá trị hiệu dụng của điện áp này là
Giá trị hiệu dụng của điện áp này là \(110\sqrt{2}\) V.
Đặt một điện áp xoay chiều vào hai đầu đoạn mạch gồm điện trở thuần R mắc nối tiếp với tụ điện có điện dung C. Điện áp hiệu dụng giữa hai đầu R là 80 V, điện áp hiệu dụng giữa hai đầu tụ điện là 60 V. Điện áp hiệu dụng giữa hai đầu đoạn mạch là
Ta có:
U = \(\sqrt{U_{R}^{2}+U_{C}^{2}}\)= 100 V.
Một máy phát điện xoay chiều một pha có phần cảm là rôto gồm 5 cặp cực (5 cực nam và 5 cực bắc). Để suất điện động do máy này sinh ra có tần số 50 Hz thì rôto phải quay với tốc độ.
Ta có:
n = \(\frac{f.60}{p}\)= 600 vòng/phút.
Khi quan sát bong bóng xà phòng hay đĩa CD thì thấy lấp lánh, nhiều màu sặc sỡ là do hiện tượng
Khi quan sát bong bóng xà phòng hay đĩa CD thì thấy lấp lánh, nhiều màu sặc sỡ là do hiện tượng giao thoa ánh sáng.
Công thoát của electron khỏi một kim loại là 6,625.10- 19J. Biết h = 6,625.10-34Js; c = 3.108m/s. Giới hạn quang điện của kim loại này là
Giới hạn quang điện của kim loại λ0 = \(\frac{hc}{A}\) = 300 nm.
Quang điện trở có nguyên tắc hoạt động dựa trên hiện tượng
Quang điện trở có nguyên tắc hoạt động dựa vào hiện tượng quang điện trong.
Trong phản ứng hạt nhân \({}_{2}^{4}He+{}_{13}^{27}Al\to {}_{15}^{30}P+X\) hạt X là.
Dùng định luật bảo toàn điện tích và bảo toàn số nuclon:
4+ 27 = 30 + A --> A = 1 ; 2 + 13 = 15 + Z --> Z = 0 , hạt X là nơtron
Hạt nhân 6027Co có cấu tạo gồm
Từ kí hiệu hạt nhân \({}_{Z}^{A}X\) được A = 60 , Z = 27
-->số proton = 27 , số nơtron N = A – Z = 60 – 27 = 33
Gọi k là hệ số nhân nơtrôn thì điều kiện để phản ứng dây chuyền xảy ra là:
Điều kiện để phản ứng dây chuyền xảy ra là k ≥ 1.
Xét một lượng chất phóng xạ xác định ban đầu khối lượng là m0 . Sau 1 năm, khối lượng chất phóng xạ giảm đi 3 lần. Hỏi sau 2 năm, khối lượng chất phóng xạ trên giảm đi bao nhiêu lần so với ban đầu.
+ gọi x là số lần lượng chất phóng xạ đã giảm so với m0 .
+ gọi t1 là thời gian 1 năm ,theo định luật phóng xạ ta có:
\(\frac{{{m}_{0}}}{3}=\frac{{{m}_{0}}}{{{2}^{\frac{{{t}_{1}}}{T}}}}\) --> t1 /T=1,5849
+gọi t2 là thời gian 2 năm ,theo định luật phóng xạ ta có:
\(\frac{{{m}_{0}}}{x}=\frac{{{m}_{0}}}{{{2}^{2x\frac{{{t}_{1}}}{T}}}}\)--> x = 9
Từ trường đều là từ trường mà các đường sức từ là các đường
Từ trường đều là từ trường mà các đường sức từ là các đường thẳng song song và cách đều nhau.
Một người đeo kính có độ tụ -1,5 dp thì nhìn xa vô cùng mà không phải điều tiết. Người này:
Mắc tật cận thị và có điểm cực viễn cách mắt 2/3 m.
Biên độ của dao động:
\({{a}_{\max }}=A{{\omega }^{2}}\Rightarrow A.{{\left( 2\pi \right)}^{2}}=40{{\pi }^{2}}\Rightarrow A=10\,\,cm\)
Gia tốc biến thiên sớm pha \(\pi \)so với li độ nên:
\({{\varphi }_{x}}={{\varphi }_{a}}-\pi =\frac{\pi }{2}-\pi =-\frac{\pi }{2}\)
Phương trình dao động của vật:
\(x=10\cos \left( 2\pi t-\frac{\pi }{2} \right)\,\,cm.\)
Sóng ngang truyền trên mặt chất lỏng với tần số 100Hz. Trên cùng phương truyền sóng, hai điểm cách nhau 15cm dao động cùng pha với nhau. Biết vận tốc truyền sóng trên dây khoảng từ 2,8 m/s đến 3,4 m/s. Vận tốc truyền sóng chính xác là
Khoảng cách của 2 điểm dao động cùng pha:
\(d=n.\lambda =0,15\Rightarrow \lambda =\frac{0,15}{n}\)
Mà vận tốc truyền sóng: \(v=\lambda .f=\frac{15}{k}(m/s)\)
Theo bài ra: \(2,8(m/s)\le k\le 3,4(m/s)\)
\(\Rightarrow 4,41\le k\le 5,36\). Vì k nguyên nên \(k=5\Rightarrow v=3(m/s)\)
Một chất điểm dao động điều hòa với phương trình x = 6cos4πt(cm). Biên độ là bao nhiêu?
Biên độ là 6cm
Cho ba vật dao động điểu hòa cùng biên độ \(A=10\,\,cm\) nhưng tần số khác nhau. Biết rằng tại mọi thời điểm li độ, vận tốc của các vật liên hệ với nhau bởi biểu thức \(\frac{{{x}_{1}}}{{{v}_{1}}}+\frac{{{x}_{2}}}{{{v}_{2}}}=\frac{{{x}_{3}}}{{{v}_{3}}}+2018\). Tại thời điểm t, các vật cách vị trí cân bằng của chúng lần lượt là 6 cm, 8 cm và \({{\text{x}}_{3}}\) . Giá trị \({{\text{x}}_{3}}\) gần giá trị nào nhất:
+ Xét đạo hàm sau: \({{\left( \frac{x}{v} \right)}^{'}}=\frac{x'.v-v'.x}{{{v}^{2}}}=\frac{{{v}^{2}}-a.x}{{{v}^{2}}}=\frac{{{\omega }^{2}}\left( {{A}^{2}}-{{x}^{2}} \right)-\left( -{{\omega }^{2}}.x \right).x}{{{\omega }^{2}}\left( {{A}^{2}}-{{x}^{2}} \right)}=\frac{{{A}^{2}}}{{{A}^{2}}-{{x}^{2}}}\,\,\,\left( 1 \right)\)
+ Xét biểu thức: \(\frac{{{x}_{1}}}{{{v}_{1}}}+\frac{{{x}_{2}}}{{{v}_{2}}}=\frac{{{x}_{3}}}{{{v}_{3}}}.\)
+ Lấy đạo hàm hai vế và áp dụng đạo hàm (1) ta có:
\({{\left( \frac{{{x}_{1}}}{{{v}_{1}}}+\frac{{{x}_{2}}}{{{v}_{2}}} \right)}^{'}}={{\left( \frac{{{x}_{3}}}{{{v}_{3}}} \right)}^{'}}+2018'\Rightarrow {{\left( \frac{{{x}_{1}}}{{{v}_{1}}} \right)}^{'}}+{{\left( \frac{{{x}_{2}}}{{{v}_{2}}} \right)}^{'}}={{\left( \frac{{{x}_{3}}}{{{v}_{3}}} \right)}^{'}}\)
\(\Rightarrow \frac{{{A}^{2}}}{{{A}^{2}}-x_{1}^{2}}+\frac{{{A}^{2}}}{{{A}^{2}}-x_{2}^{2}}=\frac{{{A}^{2}}}{{{A}^{2}}-x_{0}^{2}}\Rightarrow \frac{{{10}^{2}}}{{{10}^{2}}-{{6}^{2}}}+\frac{{{10}^{2}}}{{{10}^{2}}-{{8}^{2}}}=\frac{{{10}^{2}}}{{{10}^{2}}-x_{0}^{2}}=\frac{625}{144}\)
\(\Rightarrow {{x}_{0}}=\sqrt{\frac{1924}{25}}=8,77\,\,\left( cm \right)\)
Một con lắc lò xo được treo trên trần một thang máy. Khi thang máy đứng yên thì con lắc được kích thích dao động điều hòa theo phương thẳng đứng với chu kỳ 0,4 s, biên độ 5 cm. Vừa lúc quả cầu của con lắc đang đi qua vị trí lò xo không biến dạng theo chiều từ trên xuống thì thang máy chuyển động nhanh dần đều đi lên với gia tốc có độ lớn \(5\,\,{m}/{{{s}^{2}}}\;\). Lấy \(g={{\pi }^{2}}=10\,\,{m}/{{{s}^{2}}}\;\). Sau đó con lắc dao động với biên độ là
Ta có độ biến dạng của lò xo tại vị trí cân bằng: \(\text{x}=\Delta \ell =\frac{mg}{k}=\frac{{{T}^{2}}g}{4{{\pi }^{2}}}=4\,\,cm.\)
Xét chuyển động của con lắc với thang máy: Chọn chiều dương hướng lên. Thang máy chuyển động nhanh dần đều ở vị trí: \(\text{x}=\Delta \ell \).
Khi thang máy chuyển động, vị trí cân bằng bị dịch xuống dưới một đoạn bằng:
\(y=\Delta \ell '=\frac{m\left( g+a \right)}{k}-\frac{mg}{k}=\frac{a}{{{\omega }^{2}}}=\frac{5}{{{\left( 5\pi \right)}^{2}}}=0,02\,m=2\,cm\)
Nên li độ lúc sau là: \(\text{x}'=x+y.\)
Ta có: \(A{{'}^{2}}=x{{'}^{2}}+{{\left( \frac{v}{\omega } \right)}^{2}}={{\left( x+y \right)}^{2}}+{{\left( \frac{v}{\omega } \right)}^{2}}\)
Từ đó ta có: \(A{{'}^{2}}={{x}^{2}}+2\text{x}y+{{y}^{2}}+{{\left( \frac{v}{\omega } \right)}^{2}}={{A}^{2}}+{{y}^{2}}+2\text{x}y\) .
Thay số vào ta được: \(A{{'}^{2}}={{5}^{2}}+{{2}^{2}}+2.4.2=45\Rightarrow A'=\sqrt{45}=3\sqrt{5}\,\,cm\)
Một sóng dừng trên một sợi dây có dạng u = 40sin2,5πxcosωt (mm), trong đó u là li độ tại thời điểm t của một phần tử M trên sợi dây mà vị trí cân bằng của nó cách gốc tọa độ O đoạn x (x đo bằng mét, t đo bằng giây). Khoảng thời gian ngắn nhất giữa hai lần liên tiếp để một điểm trên bụng sóng có độ lớn của li độ bằng biên độ của điểm N cách một nút sóng 10cm là 0,125s. Tốc độ truyền sóng trên sợi dây là:
Phương trình sóng trên 1 sợi dây: \(u=40\sin 2,5\pi \cos \omega t\left( mm \right)\)
\(\Rightarrow 2,5.\pi .x=\frac{2\pi .x}{\lambda }\Rightarrow \lambda =0,8\left( m \right)\)
Biên độ dao động của N là: \({{A}_{N}}=2.A.\sin \frac{2\pi .10}{80}=A\sqrt{2}\)
Ta có góc quét: \(\Delta {{\varphi }_{{{M}_{1}}{{M}_{2}}}}=\Delta {{\varphi }_{{{M}_{3}}{{M}_{4}}}}=\frac{\pi }{2}=\omega .0,125\)
=> Tần số góc: \(\omega =4\pi \left( rad/s \right)\)
Tần số \(f=2\left( Hz \right)\)
Vận tốc truyền sóng: \({{v}_{S}}=\lambda .f=0,8.2=1,6\left( m/s \right)=160\left( cm/s \right)\)
Thực hiện thí nghiệm giao thoa ánh sáng đơn sắc bằng khe Y-âng ở không khí (chiết suất \(n=1\)). Đánh dấu điểm M trên màn, tại M có một vân sáng. Trong khoảng từ M đến vân trung tâm còn 3 vân sáng nữa. Nhúng toàn bộ hệ giao thoa vào môi trường chất lỏng thì thấy M vẫn là một vân sáng nhưng khác so với khi ở không khí một bậc. Chiết suất n của môi trường đó là
Giữa M và vân trung tâm còn 3 vân sáng nữa \(\Rightarrow \) M là vân sáng thứ 4: \({{\text{x}}_{M}}=4.\frac{\lambda D}{a}\,\,\,\,\left( 1 \right)\)
Khi nhúng toàn bộ hệ vào môi trường chiết suất n thì bước sóng giảm:
Tại cùng vị trí M, khoảng vân giảm thì bậc của vân tăng nên:
\(k'=k+1=5\Rightarrow {{x}_{M}}=5.\frac{\lambda D}{a}\,\,\left( 2 \right)\)
Từ (1) và (2) ta có:
\(4.\frac{\lambda D}{a}=5.\frac{\lambda D}{n.a}\Rightarrow n=\frac{5}{4}=1,25\)
Trong nguyên tử hidro, khi êlêctrôn chuyển động trên quỹ đạo K với bán kính \({{r}_{0}}={{5,3.10}^{-11}}m\) thì tốc độ của electron chuyển động trên quỹ đạo đó là
Khi electron chuyển động xung quanh hạt nhân thì lực điện đóng vai trò là lực hướng tâm
\({{F}_{ht}}=k\frac{\left| {{q}_{hn}}.e \right|}{{{r}^{2}}}={{m}_{e}}\frac{{{v}^{2}}}{r}\Rightarrow {{v}^{2}}=k\frac{\left| {{q}_{hn}}.e \right|}{{{m}_{e}}.r}\) (Với Hidro: \({{q}_{hn}}=\left| e \right|\))
Thay số vào ta có: \({{v}^{2}}=k\frac{\left| {{q}_{hn}}.e \right|}{{{m}_{e}}.r}={{9.10}^{9}}\frac{{{\left( {{1,6.10}^{-19}} \right)}^{2}}}{{{9,1.10}^{-31}}{{.5,3.10}^{-11}}}={{4,78.10}^{12}}\Rightarrow v={{2,19.10}^{6}}\text{ m/s}\)
Chiếu một bức xạ có bước sóng \(\lambda =0,48\,\,\mu m\) lên một tấm kim loại có công thoát \(A={{2,4.10}^{-19}}\,\,J\). Dùng màn chắn tách ra một chùm hẹp các electron quang điện và hướng chúng bay theo chiều vectơ cường độ điện trường có \(E=1000\,\,{V}/{m}\;\). Quãng đường tối đa mà electron chuyển động được theo chiều vectơ cường độ điện trường xấp xỉ là:
Áp dụng công thức Anh-xtanh: \(\frac{hc}{\lambda }=A+{{W}_{d}}\Rightarrow {{W}_{d}}=\frac{hc}{\lambda }-A\,\,\,\,\,\,\left( 1 \right)\)
Các electron quang điện \(\left( q<0 \right)\) bay theo chiều vectơ cường độ điện trường nên lực điện trường là lực cản. Do đó, electron sẽ bay được một đoạn đường \({{\text{s}}_{\max }}\) rồi dừng lại và bị kéo ngược trở lại.
Đến khi vật dừng lại \(\left( v=0 \right)\). Áp dụng định lí biến thiên động năng ta có:
\({{A}_{ms}}=0-{{W}_{d}}=-\left| e \right|.E{{s}_{\max }}\Rightarrow {{s}_{\max }}=\frac{{{W}_{d}}}{\left| e \right|.E}=\frac{1}{\left| e \right|.E}\left( \frac{hc}{\lambda }-A \right)\)
Thay số vào ta có: \({{s}_{\max }}=\frac{1}{{{1,6.10}^{-19}}.1000}\left( \frac{{{19,875.10}^{-26}}}{{{0,48.10}^{-6}}}-{{2,4.10}^{-19}} \right)=0,00109\,\,m=0,109\,cm\)
Một sợi dây AB dài 100cm căng ngang, đầu B cố định, đầu A gắn với một nhánh của âm thoa dao động điều hòa với tần số 40Hz. Trên dây AB có một sóng dừng ổn định, A được coi là nút sóng. Tốc độ truyền sóng trên dây là 20m/s. Kể cả A và B, trên dây có:
Kể cả A và B, trên dây có 5 nút và 4 bụng.
Đặt một điện áp xoay chiều \(u=U\sqrt{2}\cos \left( \omega t \right)\,\left( V \right)\) vào hai đầu mạch điện AB mắc nối tiếp theo thứ tự gồm điện trở R, cuộn dây không thuần cảm (L, r) và tụ điện C với R = r. Gọi N là điểm nằm giữa điện trở R và cuộn dây, M là điểm nằm giữa cuộn dây và tụ điện. Điện áp tức thời \({{u}_{AM}}\) và \({{u}_{NB}}\) vuông pha với nhau và có cùng một giá trị hiệu dụng là \(30\sqrt{5}\,V\). Giá trị của U bằng:
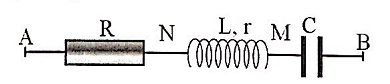
Giản đồ vectơ của mạch:
.png)
Theo đề bài ta có:
\(\left\{ \begin{align} & {{U}_{NB}}={{U}_{AM}}\Rightarrow NB=AM \\ & \angle AMH=\angle BNH \\ \end{align} \right.\Rightarrow \Delta AHM=\Delta BHN\)
( cạnh huyền và góc nhọn bằng nhau)
Suy ra :
\({{U}_{R}}={{U}_{r}}={{U}_{L}}=x\Rightarrow \left\{ \begin{align} & AH=2x \\ & MH=x \\ \end{align} \right.\Rightarrow AM={{U}_{AM}}=\sqrt{{{\left( 2x \right)}^{2}}+{{x}^{2}}}\)
Ta lại có:
\({{U}_{AM}}=30\sqrt{5}\Rightarrow \sqrt{{{\left( 2x \right)}^{2}}+{{x}^{2}}}=30\sqrt{5}\Rightarrow \left\{ \begin{align} & x=30V \\ & AH=2x=60V \\ \end{align} \right.\)
Mà:
\(\Delta AHM=\Delta BHN\Rightarrow AH=HB=2x=60\)
\(\Rightarrow AB=AH\sqrt{2}=60\sqrt{2}\left( V \right)\Rightarrow U=60\sqrt{2}\left( V \right)\)
thì tại M là:
+ Khi khoảng cách 2 khe tới màn là a thì tại M là vân sáng bậc 4 nên \({{\text{x}}_{M}}=4.\frac{\lambda D}{a}\,\,\,\,\,\,\left( 2 \right)\)
+ Nếu lần lượt giảm hoặc tăng khoảng cách \({{S}_{1}}{{S}_{2}}\) một lượng \(\Delta a\) thì tại đó là vân sáng bậc k và bậc 3k nên:
+ Nếu tăng khoảng cách \({{S}_{1}}{{S}_{2}}\) thêm \(2\Delta a\) thì tại M là: \({{\text{x}}_{M}}=k'.\frac{\lambda \text{D}}{a+2\Delta a}=k'.\frac{\lambda D}{a+a}=\frac{1}{2}k'.\frac{\lambda D}{a}\)
+ So sánh với (1) ta có: \({{\text{x}}_{M}}=\frac{1}{2}k'.\frac{\lambda \text{D}}{a}=4.\frac{\lambda \text{D}}{a}\Rightarrow k'=8\Rightarrow \)
Tại M khi đó là vân sáng bậc 8.
Một tàu phá băng công suất 16 MW. Tàu dùng năng lượng phân hạch của hạt nhân \(^{235}U\). Trung bình mỗi phân hạch tỏa ra 200 MeV. Nhiên liệu dùng trong lò là \(^{235}U\) làm giàu đến 12,5% (tính theo khối lượng). Hiệu suất của lò là 30 %. Hỏi nếu tàu làm việc liên tục trong 3 tháng thì cần bao nhiêu kg nhiên liệu (coi mỗi ngày làm việc 24 giờ, 1 tháng tính 30 ngày)
Năng lượng để tàu hoạt động trong 6 tháng
\(E=P.t={{16.10}^{6}}.30.86400={{1,24416.10}^{14}}\,\,\left( J \right)\)
Năng lượng thực tế mà phản ứng hạt nhân đã cung cấp là
\({{E}_{0}}=\frac{E}{H}=\frac{E}{0,3}={{4,1472.10}^{14}}\,\,\left( J \right)\)
Số hạt nhân Urani đã tham gia phản ứng
\(N=\frac{{{E}_{0}}}{{{200.10}^{6}}{{.1,6.10}^{-19}}}={{1,296.10}^{25}}\)
cần là: \({{m}_{U}}=\frac{N}{{{N}_{A}}}.A=\frac{{{1,296.10}^{25}}}{{{6,02.10}^{23}}}.235=5059\,g\)
cần dùng là: \({{m}_{U}}=12,5%m\Rightarrow m=\frac{{{m}_{U}}}{0,125}=40473\,g=40,473\,kg\)
Cho phản ứng hạt nhân \(_{0}^{1}n+_{3}^{6}Li\to _{1}^{3}H+\alpha \). Hạt nhân \(_{3}^{6}Li\) đứng yên, notron có động năng \({{K}_{\alpha }}=2\) MeV. Hạt \(\alpha \) và hạt nhân \(_{1}^{3}H\) bay ra theo các hướng hợp với hướng tới của notron những góc tương ứng bằng \(\theta =15{}^\circ \) và \(\varphi =30{}^\circ \). Lấy tỉ số giữa các khối lượng hạt nhân bằng tỉ số giữa các số khối của chúng. Bỏ qua bức xạ gamma. Hỏi phản ứng tỏa hay thu bao nhiêu năng lượng?
+ Theo định luật bảo toàn động lượng ta có:
\({{\overrightarrow{p}}_{n}}={{\overrightarrow{p}}_{H}}+{{\overrightarrow{p}}_{\alpha }}\)
+ Áp dụng định lí hàm sin cho tam giác ta có: \(\frac{{{p}_{\alpha }}}{\sin 30}=\frac{{{p}_{H}}}{\sin 15}=\frac{{{p}_{n}}}{\sin 135}\)
\(\Rightarrow \left\{ \begin{align} & {{p}_{\alpha }}=\frac{\sin 30}{\sin 135}.{{p}_{n}} \\ & {{p}_{H}}=\frac{\sin 15}{\sin 135}.{{p}_{n}} \\ \end{align} \right.\)
\(\Rightarrow \left\{ \begin{align} & p_{\alpha }^{2}={{\left( \frac{\sin 30}{\sin 135} \right)}^{2}}.p_{n}^{2} \\ & p_{H}^{2}={{\left( \frac{\sin 15}{\sin 135} \right)}^{2}}.p_{n}^{2} \\ \end{align} \right.\)
+ Ta lại có: \({{p}^{2}}=2m.K\) nên:
\(\left\{ \begin{align} & 2{{m}_{\alpha }}.{{K}_{\alpha }}={{\left( \frac{\sin 30}{\sin 135} \right)}^{2}}.2{{m}_{n}}.{{K}_{n}} \\ & 2{{m}_{H}}.{{K}_{H}}={{\left( \frac{\sin 15}{\sin 135} \right)}^{2}}.2{{m}_{n}}.{{K}_{n}} \\ \end{align} \right.\)
\(\Rightarrow \left\{ \begin{align} & {{K}_{\alpha }}={{\left( \frac{\sin 30}{\sin 135} \right)}^{2}}.\frac{{{m}_{n}}}{{{m}_{\alpha }}}.{{K}_{n}} \\ & {{K}_{H}}={{\left( \frac{\sin 15}{\sin 135} \right)}^{2}}.\frac{{{m}_{n}}}{{{m}_{H}}}.{{K}_{n}} \\ \end{align} \right.\)
\(\Rightarrow \left\{ \begin{align} & {{K}_{\alpha }}={{\left( \frac{\sin 30}{\sin 135} \right)}^{2}}.\frac{1}{4}.2=0,25\,\,MeV \\ & {{K}_{H}}={{\left( \frac{\sin 15}{\sin 135} \right)}^{2}}.\frac{1}{3}.2=0,089\,\,MeV \\ \end{align} \right.\)
+ Năng lượng của phản ứng:
\(E=\sum{{{K}_{sau}}}-\sum{{{K}_{truoc}}}={{K}_{H}}+{{K}_{\alpha }}-{{K}_{n}}=0,089+0,25-2=-1,66\,\,MeV\)
+ Phản ứng thu 1,66 MeV
Trong sơ đồ hình vẽ bên, R là một quang điện trở, AS là ánh sáng kích thích, A là ampe kế nhiệt lý tưởng, và V là vôn kế nhiệt lý tưởng. Số chỉ của ampe kế và vôn kế sẽ thay đổi như thế nào nếu tắt chùm sáng kích thích AS?
.png)
Ta biết rằng nguyên tắc hoạt động của quang điện trở dựa trên hiện tượng quang điện trong. Khi tắt chùm sáng kích thích, hiện tượng quang điện trong dừng xảy ra nên giá trị điện trở R của quang điện trở tăng lên.
Do đó cường độ dòng điện trong mạch \(I=\frac{\xi }{R+r}\) bị giảm đi nên số chỉ Ampe kế giảm.
Điện áp trên quang trở \({{U}_{R}}=\xi -Ir\) tăng lên làm số chỉ Vôn kế tăng.
Bắn một hạt nơtron có động năng 2 MeV vào hạt nhân \({}_{3}^{6}Li\) đang đứng yên thì thu được hạt anpha và hạt nhân X có hướng chuyển động hợp với hướng tới của hạt nơtron các góc lần lượt là 25° và 30°. Phản ứng này tỏa hay thu bao nhiêu năng lượng?
Vận dụng các định luật bảo toàn điện tích và bảo toàn số khối, ta viết được phương trình phản ứng hạt nhân đã xảy ra như sau:
\({}_{0}^{1}n+{}_{3}^{6}Li\to {}_{2}^{4}\alpha +{}_{1}^{3}X\)
Vận dụng định luật bảo toàn động lượng, ta vẽ được giản đồ các véc tơ động lượng như hình vẽ.
.png)
Theo định lí hàm số sin trong tam giác, ta có:
\(\frac{{{p}_{n}}}{\sin 125{}^\circ }=\frac{{{p}_{X}}}{\sin 25{}^\circ }=\frac{{{p}_{\alpha }}}{\sin 30{}^\circ }\)
\(\Rightarrow \frac{{{p}_{n}}}{{{p}_{X}}}=\sqrt{\frac{{{m}_{n}}{{K}_{n}}}{{{m}_{X}}{{K}_{X}}}}=\sqrt{\frac{1.2}{3.{{K}_{X}}}}=\frac{\sin 125{}^\circ }{\sin 25{}^\circ }\Rightarrow {{K}_{X}}=0,177MeV\)
\(\Rightarrow \frac{{{p}_{n}}}{{{p}_{\alpha }}}=\sqrt{\frac{{{m}_{n}}{{K}_{n}}}{{{m}_{\alpha }}{{K}_{\alpha }}}}=\sqrt{\frac{1.2}{4.{{K}_{\alpha }}}}=\frac{\sin 125{}^\circ }{\sin 30{}^\circ }\Rightarrow {{K}_{\alpha }}=0,186MeV\)
Năng lượng tỏa ra của phản ứng có thể được tính thông qua động năng của các hạt tham gia phản ứng, ta có:
\(\text{W}={{K}_{He}}+{{K}_{X}}-{{K}_{n}}=0,177+0,186-2=-1,637MeV<0\)
Do \(W<0\) nên phản ứng thu năng lượng 1,637 MeV.
Đặt điện áp xoay chiều lên hai đầu mạch điện như trong hình. Đồ thị biểu diễn sự phụ thuộc của điện áp giữa hai đầu đoạn mạch AN (1) và điện áp giữa hai đầu đoạn mạch MB (2) vào thời gian được cho trên hình vẽ. Số chỉ của vôn kế nhiệt là
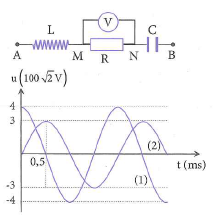
.png)
Dựa vào mối liên hệ giữa giá trị 0,5 ms và đỉnh đồ thị hình sin, ta có
\(\frac{T}{4}=0,5ms\to T=2ms\to \omega =\frac{2\pi }{T}=1000\pi \left( rad/s \right)\)
Biên độ điện áp trên đoạn AN và MB lần lượt là \({{U}_{0AN}}=400\sqrt{2}V và {{U}_{0MB}}=300\sqrt{2}V\)
Pha ban đầu của điện áp trên đoạn AN và MB lần lượt là 0 và \(-\frac{\pi }{2}\)
Từ đó ta có phương trình điện áp trên đoạn AN và MB là
\({{u}_{AN}}=400\sqrt{2}cos\left( 1000\pi t \right)V\) và \({{u}_{MB}}=300\sqrt{2}cos\left( 1000\pi t-\frac{\pi }{2} \right)V\)
Do uAN, uMB vuông pha nhau, ta dựng được giản đồ vecto như hình vẽ, từ đó ta có
\(\frac{1}{U_{R}^{2}}=\frac{1}{U_{AN}^{2}}+\frac{1}{U_{MB}^{2}}=\frac{1}{{{300}^{2}}}+\frac{1}{{{400}^{2}}}\to {{U}_{R}}=240V\).
Vậy vôn kế nhiệt chỉ 240 V, đúng bằng điện áp hiệu dụng trên điện trở R.
Một chất điểm đang dao động điều hòa với phương trình gia tốc \(a=16{{\pi }^{2}}cos\left( 2\pi t+\frac{\pi }{3} \right)cm/{{s}^{2}}\). Tính từ thời điểm ban đầu, \(t=0\), chất điểm đi qua vị trí có vận tốc bằng \(-4\pi \sqrt{3}cm/s\) lần thứ 13 tại thời điểm
.png)
Ta có \(T=\frac{2\pi }{\omega }=\frac{2\pi }{2\pi }=1s\)
\(a=16{{\pi }^{2}}cos\left( 2\pi t+\frac{\pi }{3} \right)cm/{{s}^{2}}\to v=8\pi cos\left( 2\pi t-\frac{\pi }{6} \right)cm/s\)
Trên đường tròn vận tốc, ta biểu diễn vị trí ban đầu của vận tốc (M0) và hai vị trí ứng với vận tốc bằng \(-4\pi \sqrt{3}cm/s\) \(\left( {{M}_{1}},\,{{M}_{2}} \right)\) như trên hình vẽ.
Từ đường tròn, ta suy ra trong mỗi chu kì dao động có 2 lần chất điểm có vận tốc bằng \(-4\pi \sqrt{3}cm/s\).
Tách \(13=6.2+1\to t=6T+\Delta t\).
Do hai điểm M0 và M1 đối xứng tâm trên đường tròn nên ta tính được \(\Delta \varphi =\pi \to \Delta t=\frac{T}{2}=0,5s\)
Từ đó suy ra \(t=6.1+0,5=6,5s\).
Tiến hành thí nghiệm giao thoa ánh sáng đơn sắc có bước sóng 0,4 μm với hai khe Y-âng cách nhau 0,8 mm. Gọi H là chân đường cao hạ từ khe S1 tới màn quan sát. Lúc đầu tại H có một vân tối giao thoa. Dịch màn ra xa dần thì chỉ quan sát được 2 lần tại H cho vân sáng. Trong quá trình dịch chuyền màn, khoảng cách giữa 2 vị trí của màn để tại H đạt cực đại giao thoa lần đầu và đạt cực tiểu giao thoa lần cuối là
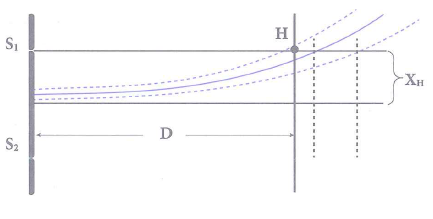
Từ công thức khoảng vân \(i=\frac{\lambda D}{a}\) ta thấy, khi màn rời xa mặt phẳng chứa hai khe thì D tăng, do đó khoảng vân i sẽ tăng dần. Việc trong quá trình di chuyển ra xa dần, tại H chỉ có hai lần cho vân sáng cho thấy vân tối lần đầu tiên là vân tối thứ 3 tính từ vân trung tâm, và trong khoảng từ H đến vân sáng trung tâm khi đó chỉ có hai vân sáng (xem hình vẽ).
Khi màn ở vị trí mà H ứng với cực đại giao thoa lần đầu tiên (vân sáng bậc 2) trong quá trình dịch chuyển màn ra xa dần thì khoảng cách từ H tới vân sáng trung tâm là: \({{x}_{H}}=\frac{a}{2}=2\frac{\lambda D}{a}\to D=0,4m\)
Khi màn ở vị trí mà H là cực tiểu lần cuối, tức là H ứng với vân tối thứ nhất (gần vân sáng trung tâm nhất), ta có:
\(\frac{a}{2}=\frac{\lambda {D}'}{a}\Rightarrow {D}'=1,6m\)
Vậy 2 vị trí màn cách nhau \({D}'-D=1,6-0,4=1,2m\).
Trên một sợi dây đàn hồi căng ngang đang có sóng dừng ổn định, biên độ dao động tại bụng sóng bằng 10 cm, và khoảng cách giữa hai nút sóng gần nhau nhất bằng 36 cm. Tại điểm N trên dây có một nút sóng. Hai điểm E, F trên dây nằm về cùng một phía so với N. Các khoảng cách trên phương truyền sóng từ E và F tới N lần lượt bằng 6 cm và 27 cm. Trong quá trình dao động, khoảng cách xa nhất giữa hai phần tử dây tại E và F xấp xỉ bằng
.png)
Khoảng cách giữa hai nút sóng gần nhau nhất
\(NM=\frac{\lambda }{2}=36cm\to \lambda =72cm\).
Nhìn vào hình vẽ, dựa vào đặc tính của đồ thị hình sin, do điểm E cách N một khoảng là \(6cm=\frac{\lambda }{12}\) nên biên độ dao động tại E là \({{A}_{E}}=5cm\).
Tương tự như vậy, do điểm F cách N một khoảng \(27cm=\frac{3\lambda }{8}\) nên suy ra biên độ dao động tại F là \({{A}_{F}}=5\sqrt{2}cm\).
E, F nằm trong cùng một bó sóng nên hai phần tử dây tại đó dao động cùng pha, suy ra khoảng cách xa nhất giữa hai phần tử dây trong quá trình dao động là \({{d}_{max}}=\sqrt{E{{F}^{2}}+{{\left( {{A}_{F}}-{{A}_{E}} \right)}^{2}}}=21,1cm\) đạt được khi hai phần tử này cùng đi qua vị trí biên.

