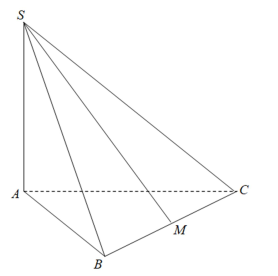
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A , SA vuông góc với mặt phẳng đáy, \(S A=\frac{\sqrt{2} a}{2}, A B=A C=a\) . Gọi M là trung điểm của BC ( xem hình vẽ ). Tính góc giữa đường thẳng SM và mặt phẳng (ABC).

Điểm M trong hình vẽ bên là điểm biểu diễn cho số phức z .

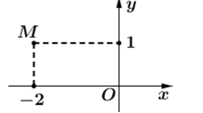
Ký hiệu\(\bar z\) là số phức liên hợp của z . Khi đó mệnh đề nào sau đây là đúng?
 

Cho a và b là hai số thực dương thỏa mãn \(\log _{2}(a b)=\log _{4}\left(a b^{4}\right)\). Mệnh đề nào dưới đây đúng ?
 

Cho hình hộp \(A B C D \cdot A^{\prime} B^{\prime} C^{\prime} D'\) có các cạnh bằng 2a . Biết \(\widehat{B A D}=60^{\circ}, \widehat{A^{\prime} A B}=\widehat{A^{\prime} A D}=120^{\circ}\) Tính thể tích V của khối hộp \(A B C D \cdot A^{\prime} B^{\prime} C^{\prime} D^{\prime}\)

Tính tích phân \(I=\int\limits_{1}^{e} \frac{\sqrt{1+3 \ln x}}{x} \mathrm{d} x\) bằng cách đặt t\(t=\sqrt{1+3 \ln x}\) . Mệnh đề nào sau đây đúng?

Cho hàm sô y =f(x) thỏa mãn \(\left[f^{\prime}(x)\right]^{2}+f(x) \cdot f^{\prime \prime}(x)=x^{3}-2 x, \forall x \in R \text { và } f(0)=f^{\prime}(0)=2\) Tính giá trị của \(T=f^{2}(2)\)
 

Trong không gian toạ độ Oxyz, cho đường thẳng\(d:\left\{\begin{array}{l} x=2+3 t \\ y=5-4 t,(t \in \mathbb{R}) \\ z=-6+7 t \end{array}\right.\) và điểm A(1;2;3) . Đường thẳng đi qua A và song song với đường thẳng d có vectơ chỉ phương là:

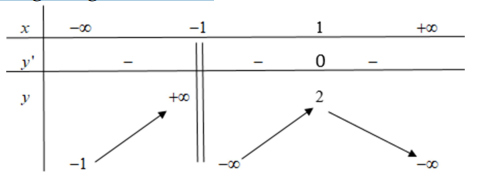
Đồ thị hàm số \(y=f(x)\) với bảng biên thiên như hình vẽ có tổng số đường tiệm cận ngang và tiệm cận đứng bằng bao nhiêu?

Đội học sinh giỏi trường trung học phổ thông chuyên bến tre gồm có 8 học sinh khối 12, 6 học sinh khối 11 và 5 học sinh khối 10. Chọn ngẫu nhiên 8 học sinh. Xác suất để trong 8 học sinh được chọn có đủ 3 khối là

Cho hình chóp tứ giác S.ABCD  có đáy ABCD là hình vuông cạnh a và \(S A \perp(A B C)\), SA=3a . Thể tích của khối chóp S.ABCD là
 

Trong không gian với hệ tọa độ Oxyz , cho ba điểm \(A(2 ;-1 ; 3), B(4 ; 0 ; 1) \text { và } C(-10 ; 5 ; 3)\) Vectơ nào dưới đây là vectơ pháp tuyến của mặt phẳng (ABC)?
 

Cho hình chữ nhật ABCD có \(A C=2 a \sqrt{2} \text { và } \widehat{A C B}=45^{\circ}\) . Quay hình chữ nhật ABCD quanh cạnh AB thì đường gấp khúc ADCB tạo thành hình trụ. Diện tích toàn phần\( S_{tp}\) của hình trụ là
 

Phương trình\(7^{2 x^{2}+5 x+4}=49\) có tổng các nghiệm bằng

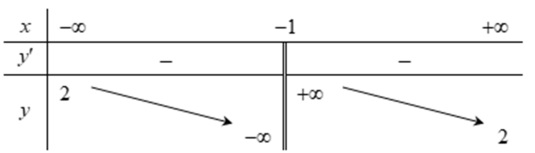
Cho bảng biến thiên của hàm số y =f(x) như hình vẽ. Phát biểu nào sau đây là sai?

Trong không gian Oxyz , hình chiếu vuông góc của điểm M (1;0;2) trên mặt phẳng (Oyz) có tọa độ là