Đề thi thử tốt nghiệp THPT QG môn Toán năm 2020 - Trường THPT chuyên Bến Tre lần 1
Đề thi thử tốt nghiệp THPT QG môn Toán năm 2020 - Trường THPT chuyên Bến Tre lần 1
-
Hocon247
-
50 câu hỏi
-
90 phút
-
51 lượt thi
-
Dễ
Tham gia [ Hs Hocon247.com ] - Cộng Đồng Luyện Thi Trực Tuyến để được học tập những kiến thức bổ ích từ HocOn247.com
Tập nghiệm của bất phương trình \(\log _{2}(x+1)<\log _{2}(3-x)\) là
ĐK: \(-1<x<3\)
Ta có: \(\log _{2}(x+1)<\log _{2}(3-x) \Leftrightarrow(x+1)<(3-x) \Leftrightarrow x<1\)
Kết hợp với điều kiện ta có tập nghiệm của bất phương trình là \(S=(-1 ; 1)\)
Cho hàm số y=f(x) liên tục trên \(\mathbb{R}\) và có bảng xét dấu f'(x) như sau
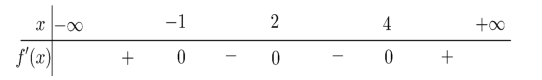
Hàm số y = f(x) có bao nhiêu điểm cực trị?
Từ bảng xét dấu của \(y=f'(x)\) ta thấy f\(y=f'(x)\) đổi dấu qua các điểm x=-1 và x = 4 nên hàm số có hai điểm cực trị.
Trong không gian Oxyz , điểm nào dưới đây thuộc đường thẳng \(d: \frac{x-3}{2}=\frac{y-4}{1}=\frac{z+1}{2} ?\)
Xét điểm \(N(3 ; 4 ;-1)\)
\(\frac{3-3}{2}=\frac{4-4}{1}=\frac{-1+1}{2}\)
Từ đây ta suy ra \(N(3 ; 4 ;-1) \in d\)
Đường cong trong hình vẽ là đồ thị của hàm số nào ?
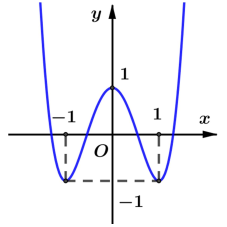
Dựa vào hình dạng đồ thị nhậ thấy đây là đồ thị hàm trùng phương nên loại đáp án C.
Mặt khác, hàm số đạt cực đại tại x = 0 , đạt cực tiểu tại \(x=\pm1\)
Mà \(y(\pm 1)=-1\) nên nhận đáp án D
Với a là số thực dương bất kì, mệnh đề nào dưới đây đúng?
Áp dụng công thức logarit của một lũy thừa ta có \(\log \left(a^{3}\right)=3 \log a\)
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A , SA vuông góc với mặt phẳng đáy, \(S A=\frac{\sqrt{2} a}{2}, A B=A C=a\) . Gọi M là trung điểm của BC ( xem hình vẽ ). Tính góc giữa đường thẳng SM và mặt phẳng (ABC).
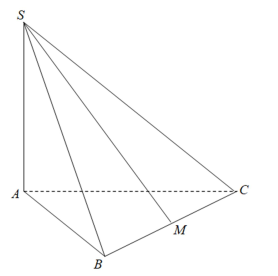
Do SA vuông góc với mặt phẳng (ABC) nên AM là hình chiếu vuông góc của SM trên mặt phẳng (ABC)
Vậy góc giữa đường thẳng SM và mặt phẳng ( ABC) là góc giữa SM và AM hay \(\widehat {SMA}\)
Vì tam giác ABC là tam giác vuông cân tại A nên: \(A M=\frac{1}{2} B C=\frac{a \sqrt{2}}{2}\)
Tam giác SAM vuông tại A và có \(S A=A M=\frac{a \sqrt{2}}{2}\) nên tam giác SAM vuông cân tại A.
\(\Rightarrow \widehat{S M A}=45^{\circ}\)
Tính tích phân \(I=\int\limits_{1}^{e} \frac{\sqrt{1+3 \ln x}}{x} \mathrm{d} x\) bằng cách đặt t\(t=\sqrt{1+3 \ln x}\) . Mệnh đề nào sau đây đúng?
\(I=\int\limits_{1}^{e} \frac{\sqrt{1+3 \ln x}}{x} \mathrm{d} x\)
\(\text { Đặt } t=\sqrt{1+3 \ln x} \Leftrightarrow t^{2}=1+3 \ln x \Rightarrow 2 t \mathrm{d} t=\frac{3}{x} \mathrm{d} x\)
Đổi cận \(\text { Với } x=1 \Rightarrow t=1 ; \text { với } x=e \Rightarrow t=2\)
Khi đó: \(I=\frac{2}{3} \int_{1}^{2} t^{2} \mathrm{d} t\)
Trên mặt phẳng tọa độ Oxy , điểm biểu diễn số phức \(z=(2+i)^{2}\) có tọa độ là
Ta có:
\(z=(2+i)^{2}=3+4 i \Rightarrow\)số phức z có điểm biểu diễn là \(Q(3 ; 4)\)
Hàm số \(y=x^{3}+3 x^{2}+3 x-10\)có bao nhiêu điểm cực trị?
Ta có:\(y^{\prime}=3 x^{2}+6 x+3=0 \Leftrightarrow x=-1 \Rightarrow y^{\prime} \geq 0 \forall x \in \mathbb{R}\)
Vậy hàm số không có cực trị.
Tiệm cận ngang của đồ thị hàm số \(y=\frac{5}{x-1}\) là đường thẳng có phương trình
Ta có \(\lim\limits _{x \rightarrow+\infty} y=0 \Rightarrow y=0\) là đường tiệm cận ngang .
Thể tích V của khối nón có chiều cao \(h = 6 \)và bán kính đáy \(R = 4 \)là :
Thể tích khối nón là: \(V=\frac{1}{3} \pi R^{2} h=\frac{1}{3} \pi .4^{2} .6=32 \pi\)
Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình vuông cạnh a và \(S A \perp(A B C)\), SA=3a . Thể tích của khối chóp S.ABCD là
Thể tích của khối chóp S.ABCD là \(V=\frac{1}{3} \cdot S A \cdot A B^{2}=\frac{1}{3} \cdot 3 a \cdot a^{2}=a^{3}\)
Cho a và b là hai số thực dương thỏa mãn \(\log _{2}(a b)=\log _{4}\left(a b^{4}\right)\). Mệnh đề nào dưới đây đúng ?
\(\begin{array}{l} \log _{2}(a b)=\log _{4}\left(a b^{4}\right) \Leftrightarrow \log _{2}(a b)=\frac{1}{2} \log _{2}\left(a b^{4}\right) \\ \Leftrightarrow \log _{2}(a b)^{2}=\log _{2}\left(a b^{4}\right) \Leftrightarrow a^{2} b^{2}=a b^{4} \Leftrightarrow a=b^{2} \end{array}\)
Trong không gian Oxyz , mặt cầu \((S): x^{2}+y^{2}+6 x-4 y+2 z-2=0\) có bán kính là
Mặt cầu có tâm I(-3;2;-1)
\(R=\sqrt{(-3)^{2}+2^{2}+(-1)^{2}+2}=4\)
Cho bảng biến thiên của hàm số y =f(x) như hình vẽ. Phát biểu nào sau đây là sai?
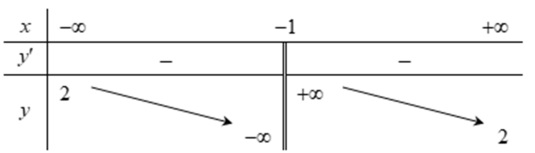
Phát biểu D sai vì hàm số nghịch biến trên \((-\infty ;-1) \text { và }(-1 ;+\infty)\)
Tập xác định của hàm số \(y=\left(x^{2}-4 x+3\right)^{-1}\) là
Hàm số xác định khi \(x^{2}-4 x+3 \neq 0 \Leftrightarrow\left[\begin{array}{l} x \neq 1 \\ x \neq 3 \end{array}\right.\)
Cho hình chữ nhật ABCD có \(A C=2 a \sqrt{2} \text { và } \widehat{A C B}=45^{\circ}\) . Quay hình chữ nhật ABCD quanh cạnh AB thì đường gấp khúc ADCB tạo thành hình trụ. Diện tích toàn phần\( S_{tp}\) của hình trụ là
Hình chữ nhật ABCD có \(A C=2 a \sqrt{2} \text { và } \widehat{A C B}=45^{\circ}\) nên là hình vuông.
\(\Rightarrow A B=B C=C D=D A=2 a\)
Khi quay hình chữ nhật quanh cạnh AB ta được hình trụ có chiều cao \(h=A B=2 a\) và bán kính đáy là \(r=B C=2 a\) .
\(\Rightarrow S_{t p}=2 \pi r l=2 \pi r h=8 \pi a^{2}\)
Giá trị nhỏ nhất của hàm số \(f(x)=-x^{3}-3 x^{2}+9 x+1\) trên đoạn [-2;1] bằng-10
\(\begin{array}{l} f^{\prime}(x)=-3 x^{2}-6 x+9 \\ f^{\prime}(x)=0 \Leftrightarrow\left[\begin{array}{l} x=1\in[-2;1] \\ x=-3 \notin [-2;1] \end{array}\right. \end{array}\)
\(f(-2)=-21 ; f(1)=6\)
Vậy giá trị nhỏ nhất của hàm số đã cho trên đoạn [-2;1] là -21
Trong không gian Oxyz, cho mặt phẳng\((P): 5 x-2 y+z+6=0\) Vectơ nào dưới đây là một vectơ pháp tuyến của (P) ?
Ta có \((P): 5 x-2 y+z+6=0 \Rightarrow \overrightarrow{n_{3}}=(5 ;-2 ; 1)\) là một vectơ pháp tuyến của (P).
Phương trình\(7^{2 x^{2}+5 x+4}=49\) có tổng các nghiệm bằng
Ta có:
\(\begin{array}{l} 7^{2 x^{2}+5 x+4}=49 \Leftrightarrow 7^{2 x^{2}+5 x+4}=7^{2} \Leftrightarrow 2 x^{2}+5 x+4=2 \\ \Leftrightarrow 2 x^{2}+5 x+2=0 \Leftrightarrow\left[\begin{array}{l} x=-2 \\ x=-\frac{1}{2} \end{array}\right. \end{array}\)
Vậy tổng các nghiệm là \(-5\over 2\)
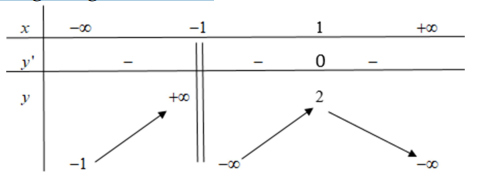
Đồ thị hàm số \(y=f(x)\) với bảng biên thiên như hình vẽ có tổng số đường tiệm cận ngang và tiệm cận đứng bằng bao nhiêu?
Ta có:
\(\lim\limits _{x \rightarrow-\infty} f(x)=-1\Rightarrow \) đồ thị hàm số có tiệm cận ngang y = - 1.
\(\lim \limits_{x \rightarrow-1^{-}} f(x)=+\infty ; \lim\limits _{x \rightarrow-1^{+}} f(x)=-\infty\Rightarrow \) đồ thị hàm số có tiệm cận đứng x = - 1.
Vậy tổng số đường tiệm cận ngang và tiệm cận đứng là 2.
Trong không gian toạ độ Oxyz, cho đường thẳng\(d:\left\{\begin{array}{l} x=2+3 t \\ y=5-4 t,(t \in \mathbb{R}) \\ z=-6+7 t \end{array}\right.\) và điểm A(1;2;3) . Đường thẳng đi qua A và song song với đường thẳng d có vectơ chỉ phương là:
Vec tơ chỉ phương của d là \(\vec{u_d}(3 ;-4 ; 7)\)
Đường thẳng đi qua A và song song với đường thẳng d nhận vec tơ chỉ phương của d làm vectơ chỉ phương.
\(\text { Vậy}: \vec{u}(3 ;-4 ; 7)\)
Cho hàm số\(y=f(x)=x^{4}-5 x^{2}+4\) có đồ thị như hình vẽ bên. Gọi S là diện tích hình phẳng giới hạn bởi đồ thị hàm số y=f(x), trục hoành và hai đường thẳng\(x=0, x=2\) (miền phẳng được gạch chéo trong hình vẽ). Mệnh đề nào sau đây sai?
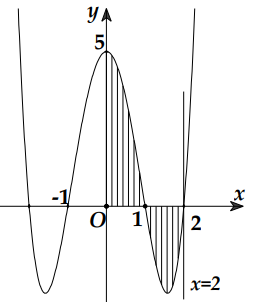
Diện tích hình phẳng giới hạn bởi đồ thị hàm số y=f(x), trục hoành và hai đường thẳng x=0, x=2 được tính bởi công thức
\(\begin{array}{l} S=\int\limits_{0}^{2}|f(x)| \mathrm{d} x=\int\limits_{0}^{1}|f(x)| \mathrm{d} x+\int\limits_{1}^{2}|f(x)| \mathrm{d} x \\ \Rightarrow S=\left|\int\limits_{0}^{1} f(x) \mathrm{d} x\right|+\left|\int\limits_{1}^{2} f(x) \mathrm{d} x\right| \\ \Rightarrow S=\int\limits_{0}^{1} f(x) \mathrm{d} x-\int\limits_{1}^{2} f(x) \mathrm{d} x \end{array}\)
Vậy \(S=\left|\int\limits_{0}^{2} f(x) \mathrm{d} x\right|\) là mệnh đề sai.
Trong không gian Oxyz , hình chiếu vuông góc của điểm M (1;0;2) trên mặt phẳng (Oyz) có tọa độ là
Hình chiếu vuông góc của điểm M (1;0;2) trên mặt phẳng (Oyz) là \(M^{\prime}(0 ; 0 ; 2)\)
Trong không gian với hệ tọa độ Oxyz , cho ba điểm \(A(2 ;-1 ; 3), B(4 ; 0 ; 1) \text { và } C(-10 ; 5 ; 3)\) Vectơ nào dưới đây là vectơ pháp tuyến của mặt phẳng (ABC)?
Ta có:
\(\overrightarrow{A B}=(2 ; 1 ;-2), \overrightarrow{A C}=(-12 ; 6 ; 0) \Rightarrow[{\overrightarrow{A B}, \overrightarrow{A C}}]=(12 ; 24 ; 24)=12(1 ; 2 ; 2)\)
Vậy vectơ pháp tuyến của mặt phẳng \((A B C) \text { là } \vec{n}=(1 ; 2 ; 2)\)
Tổng tất cả các nghiệm của phương trình \(2^{2 x+1}-5 \cdot 2^{x}+2=0\) bằng bao nhiêu?
\(2^{2 x+1}-5.2^{x}+2=0 \Leftrightarrow 2.2^{2 x}-5.2^{x}+2=0 \Leftrightarrow\left[\begin{array}{l} 2^{x}=2 \\ 2^{x}=\frac{1}{2} \end{array} \Leftrightarrow\left[\begin{array}{l} x=1 \\ x=-1 \end{array}\right.\right.\)
Vậy tổng tất cả các nghiệm bằng 0 .
Một mặt cầu có đường kính bằng a có diện tích S bằng bao nhiêu?
Bán kính của mặt cầu là: \(R=\frac{a}{2}\)
Diện tích của mặt cầu là: \(S=4 \pi R^{2}=4 \pi \frac{a^{2}}{4}=\pi a^{2}\)
Gọi l, h, R lần lượt là độ dài đường sinh, chiều cao và bán kính đáy của một hình nón ( N) . Diện tích xung quanh \(S_{x q}\)của hình nón (N) là
Diện tích xung quanh của hình nón ( N) là:
\(S_{x q}=\pi R l\)
Cho số phức z thỏa mãn \((3+2 i) z+(2-i)^{2}=4+i\). Hiệu phần thực và phần ảo của số phức z là
\((3+2 i) z+(2-i)^{2}=4+i \Leftrightarrow(3+2 i) z=4+i-(2-i)^{2} \Leftrightarrow(3+2 i) z=4+i-\left(4-4 i+i^{2}\right)\)
\(\Leftrightarrow(3+2 i) z=1+5 i \Leftrightarrow z=\frac{1+5 i}{3+2 i} \Leftrightarrow z=1+i\)
Vậy hiệu phần thực và phần ảo của số phức z là 0.
Cho hàm đa thức bậc bốn y= f(x) có đồ thị như hành vẽ bên dưới. Số nghiệm phương trình \(3 f(x)=2\) là
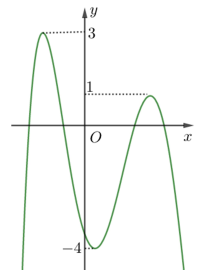
\(3 f(x)=2(1) \Leftrightarrow f(x)=\frac{2}{3}\)
Số nghiệm phương trình (1) là số giao điểm đồ thị hàm số \(y=f(x)\) và đường thẳng \(y=\frac{2}{3}\) .
Từ hình vẽ ta thấy đồ thị hàm số \(y=f(x)\) và đường thẳng \(y=\frac{2}{3}\) cắt nhau tại 4 điểm phân biệt. Vậy phương trình \(3 f(x)=2\) có 4 nghiệm phân biệt.
Điểm M trong hình vẽ bên là điểm biểu diễn cho số phức z .
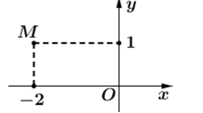
Ký hiệu\(\bar z\) là số phức liên hợp của z . Khi đó mệnh đề nào sau đây là đúng?
Ta có: \(M(-2 ; 1) \Rightarrow z=-2+i \Rightarrow \bar{z}=-2-i\)
Họ nguyên hàm của hàm số \(f(x)=x^{2}+3\) là
Ta có:
\(\int f(x) \mathrm{d} x=\int\left(x^{2}+3\right) \mathrm{d} x=\int x^{2} \mathrm{d} x+\int 3 \mathrm{d} x=\frac{x^{3}}{3}+3 x+C\)
Cho cấp số nhân \((u_n)\) un với\(u_{1}=1, u_{3}=3\). Tính giá trị của \(u_7\) ?
Ta có:
công bội \(u_3=u_1.q^2\Rightarrow q=\sqrt{3}\)
Khi đó:
\(u_7=u_1.q^6=1.(\sqrt3)^6=9\)
Kí hiệu z0 là nghiệm phức có phần thực âm và phần ảo dương của phương trình \(z^{2}+2 z+10=0\) . Trên mặt phẳng tọa độ, điểm nào dưới đây là điểm biểu diễn của số phức \(w=i z_{0}\) ?
Ta có: \(z^{2}+2 z+10=0 \Leftrightarrow\left[\begin{array}{l} z=-1+3 i \\ z=-1-3 i \end{array}\right.\)
Vì \(z_0\) là nghiệm phức có phần thực âm và phần ảo dương nên \(z_{0}=-1+3 i\)
\(\Rightarrow w=i z_{0}=i(-1+3 i)=-i+3 i^{2}=-3-i\)
Vậy điểm biểu diễn là \(M(-3 ;-1)\)
Kí hiệu\(P_{n}, A_{n}^{k}, C_{n}^{k}\) lần lượt là số các hoán vị của tập có n phần tử, số các chỉnh hợp chập k của tập có n phần tử, số các tổ hợp chập k của tập có n phần tử với ,\(k, n \in \mathbb{N}\) ,\(1 \leq k \leq n\) . Trong các đẳng thức sau, đẳng thức nào sai?
Ta có công thức \(A_{n}^{k}=\frac{n !}{(n-k) !}\)
Suy ra \(A_{n}^{n}=\frac{n !}{(n-n) !}=n !\). Vậy C sai.
Cho \(\int\limits_{1}^{2} f(x) \mathrm{d} x=-3 \text { và } \int\limits_{2}^{3} f(x) \mathrm{d} x=4\). Khi đó \(\int\limits_{1}^{3} f(x)dx\) bằng
Ta có:
\(\int\limits_{1}^{3} f(x) \mathrm{d} x=\int\limits_{1}^{2} f(x) \mathrm{d} x+\int\limits_{2}^{3} f(x) \mathrm{d} x=-3+4=1\)
Rút gọn biểu thức \(P=x^{\frac{1}{2}} \sqrt[8]{x}\)
Ta có: \(P=x^{\frac{1}{2}} \sqrt[8]{x}=x^{\frac{1}{2}} \cdot x^{\frac{1}{8}}=x^{\frac{1}{2}+\frac{1}{8}}=x^{\frac{5}{8}}\)
Thể tích khối lăng trụ có diện tích đáy là B và chiều cao là h được tính bởi công thức
Theo công thức tính thể tích khối lăng trụ ta có \(V=B h\)
Gọi S là tập hợp tất cả các giá trị nguyên của tham số m để đường thẳng \(d: y=-x+m\) cắt đồ thị hàm số \(y=\frac{-2 x+1}{x+1}\) tại hai điểm phân biệt A B , sao cho\(A B \leq 2 \sqrt{2}\). Tổng giá trị các phần tử của S bằng
Phương trình hoành độ giao điểm: \(\frac{-2 x+1}{x+1}=-x+m(1)\)
ĐK: \(x \neq-1\)
(1)\(\Rightarrow \frac{-2 x+1}{x+1}=-x+m\)
\(\begin{array}{l} \Leftrightarrow-2 x+1=(-x+m)(x+1) \\ \Leftrightarrow-x^{2}+(m+1) x+m-1=0(2) \end{array}\)
Để đường thẳng \(d: y=-x+m\) cắt đồ thị hàm số \(y=\frac{-2 x+1}{x+1}\) tại hai điểm phân biệt A B, thì phương trình (2) có 2 nghiệm phân biệt khác -1
\(\Leftrightarrow\left\{\begin{array}{l} \Delta>0 \\ -3 \neq 0 \end{array} \Leftrightarrow m^{2}+6 m-3>0\right.\)
\(\Leftrightarrow m \in(-\infty ;-3-2 \sqrt{3}) \cup(-3+2 \sqrt{3} ;+\infty) \text { (3). }\)
Gọi \(A\left(x_{A} ;-x_{A}+m\right), B\left(x_{B} ;-x_{B}+m\right)\) là tọa độ giao điểm:
Theo đề bài ta có:
\(\begin{array}{l} A B \leq 2 \sqrt{2} \Leftrightarrow \sqrt{\left(x_{B}-x_{A}\right)^{2}+\left(x_{B}-x_{A}\right)^{2}} \leq 2 \sqrt{2} \\ \Leftrightarrow 2\left(x_{B}-x_{A}\right)^{2}=8 \Leftrightarrow x_{B}^{2}-2 x_{A} x_{B}+x_{A}^{2}-4 \leq 0 \\ \Leftrightarrow\left(x_{A}+x_{B}\right)^{2}-4 x_{A} \cdot x_{B}-4 \leq 0 \\ \Leftrightarrow(m+1)^{2}-4(1-m)-4<0 \end{array}\)
\(\Leftrightarrow m^{2}+6 m-7<0 \Leftrightarrow m \in(-7 ; 1)(4)\)
Từ (3) và (4) ta có: \(m \in(-7 ;-3-2 \sqrt{2}) \cup(-3+2 \sqrt{2} ; 1)\)
\(Vì \, m \in \mathbb{Z} \Rightarrow m \in\{-6;0\}\)
Vây tổng các phần tử của S là -6
Đội học sinh giỏi trường trung học phổ thông chuyên bến tre gồm có 8 học sinh khối 12, 6 học sinh khối 11 và 5 học sinh khối 10. Chọn ngẫu nhiên 8 học sinh. Xác suất để trong 8 học sinh được chọn có đủ 3 khối là
Số phần tử không gian mẫu: \(n(\Omega)=C_{19}^{8}=75582\)
Gọi A là biến cố:” trong 8 học sinh được chọn có đủ 3 khối”.
Ta có: \(n(A)=C_{19}^{8}-\left(C_{14}^{8}+C_{13}^{8}+C_{11}^{8}-C_{8}^{8}\right)=21128\)
\(P(A)=\frac{71128}{75582}\)
Cho hàm số y=f(x) biết hàm số f(x) có đạo hàm f'(x) và hàm số y=f'(x) có đồ thị như hình vẽ . Đặt \(g(x)=f(x+1)\) . Kết luận nào sau đây đúng?
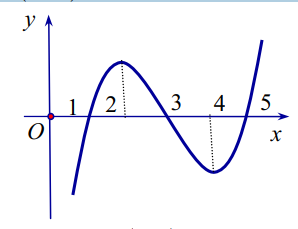
Ta có: \(g^{\prime}(x)=f^{\prime}(x+1)\)
Hàm số g(x) đồng biến \(\Leftrightarrow g^{\prime}(x)>0 \Leftrightarrow f^{\prime}(x+1)>0 \Leftrightarrow\left[\begin{array}{l} x+1>5 \\ 1<x+1<3 \end{array} \Leftrightarrow\left[\begin{array}{l} x>4 \\ 0<x<2 \end{array}\right.\right.\)
Hàm số g(x) nghịch biến \(\Leftrightarrow g^{\prime}(x)<0 \Leftrightarrow f^{\prime}(x+1)>0 \Leftrightarrow\left[\begin{array}{l} 3<x+1<5 \\ x+1<1 \end{array} \Leftrightarrow\left[\begin{array}{l} 2<x<4 \\ x<0 \end{array}\right.\right.\)
Vậy hàm số g(x) đồng biến trên khoảng\((0 ; 2) ;(4 ;+\infty)\) và nghịch biến trên khoảng \((2 ; 4) ;(-\infty ; 0)\)
Một người gởi vào ngân hàng với lãi suất 7,5% / năm với hình thức lãi kép. Hỏi sau ít nhất bao nhiêu năm thì người ấy có số tiền lãi lớn hơn số tiền gốc ban đầu? Giả định trong suốt thời gian gởi, lãi suất không đổi và người đó không rút tiền ra.
Gọi A là số tiền người đó gửi vào ban đầu.
Số tiền người ấy nhận được cả vốn lẫn lãi sau n (năm) là:
\(T_{n}=A(1+7,5 \%)^{n}\)
Theo đề ta có:
\(T_{n}-A>A \Leftrightarrow T_{n}>2 A \Leftrightarrow A(1+7,5 \%)^{n}>2 A \Leftrightarrow(1+7,5 \%)^{n}>2 \Leftrightarrow n>9,58\)
Vậy sau 10 năm thì người ấy có số tiền lãi lớn hơn số tiền gốc ban đầu.
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , SA=2a và vuông góc với (ABCD) . Gọi M là trung điểm của SD . Tính khoảng cách d giữa hai đường thẳng SB và CM.
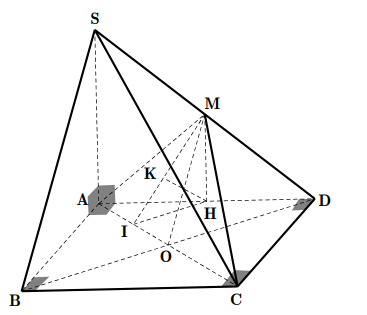
Gọi \(O=A C \cap B D\)
Vì ABCD là hình vuông cạnh a nên O là trung điểm của BD mà M là trung điểm của SD nên OM// SB / suy ra SB//(ACM).
Do đó \(d(S B, C M)=d(S B,(A C M))=d(B,(A C M))=d(D,(A C M))\)
Gọi H là trung điểm của AD nên \(M H / / S A \Rightarrow M H \perp(A B C D)\)
\(\Rightarrow d(S B, C M)=d(D,(A C M))=2 d(H,(A C M))\)
Kẻ \(H I \perp A C \Rightarrow(M H I) \perp(M A C)\) theo giao tuyến MI.
Kẻ \(H K \perp M I \Rightarrow H K \perp(A C M)\) hay \(d(H,(A C M))=H K\)
Ta có:
\(H I=\frac{1}{2} O D=\frac{1}{4} B D=\frac{1}{4} \sqrt{A B^{2}+A D^{2}}=\frac{a \sqrt{2}}{4}, M H=\frac{1}{2} S A=a\)
suy ra \(\frac{1}{H K^{2}}=\frac{1}{H M^{2}}+\frac{1}{H I^{2}} \Leftrightarrow \frac{1}{H K^{2}}=\frac{1}{a^{2}}+\frac{1}{\left(\frac{a \sqrt{2}}{4}\right)^{2}} \Leftrightarrow \frac{1}{H K^{2}}=\frac{9}{a^{2}} \Leftrightarrow H K=\frac{a}{3}\)
Vậy \(d(S B, C M)=2 d(H,(A C M))=2 H K=\frac{2 a}{3}\)
Cho hàm sô y =f(x) thỏa mãn \(\left[f^{\prime}(x)\right]^{2}+f(x) \cdot f^{\prime \prime}(x)=x^{3}-2 x, \forall x \in R \text { và } f(0)=f^{\prime}(0)=2\) Tính giá trị của \(T=f^{2}(2)\)
ta có:
\(\left[f^{\prime}(x)\right]^{2}+f(x) \cdot f^{''}(x)=x^{3}-2 x, \forall x \in R\)
\(\Leftrightarrow\left(f^{\prime}(x) \cdot f(x)\right)^{\prime}=x^{3}-2 x, \forall x \in R\)
Lấy nguyên hàm hai vế ta có:
\(\begin{array}{l} \int\left(f^{\prime}(x) \cdot f(x)\right)^{\prime} d x=\int\left(x^{3}-2 x\right) d x \\ \Leftrightarrow f^{\prime}(x) \cdot f(x)=\frac{x^{4}}{4}-x^{2}+C \end{array}\)
Theo đề bài ta có: \(f^{\prime}(0) \cdot f(0)=C=4\)
\(\begin{array}{l} \int\limits_{0}^{2} f^{\prime}(x) \cdot f(x) \cdot d x=\int\limits_{0}^{2}\left(\frac{x^{4}}{4}-x^{2}+4\right) d x \\ \left.\Leftrightarrow \frac{f^{2}(x)}{2}\right|_{0} ^{2}=\frac{44}{15} \quad \Leftrightarrow f^{2}(2)=\frac{268}{15} \end{array}\)
Một hình trụ có bán kính đáy bằng chiều cao và bằng a . Một hình vuông ABCD có AB, CD là hai dây cung của hai đường tròn đáy và mặt phẳng (ABCD) không vuông góc với đáy. Diện tích hình vuông đó bằng
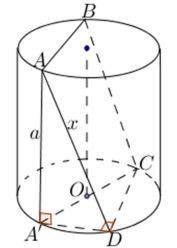
Kẻ đường sinh A A' . Khi đó ta có
\(\left\{\begin{array}{l} C D \perp A D \\ C D \perp A^{\prime} A \end{array} \Rightarrow C D \perp\left(A^{\prime} A D\right) \Rightarrow C D \perp A^{\prime} O \Rightarrow \widehat{A^{\prime} D C}=90^{\circ}\right.\)
Ta có \(\widehat {ADC}\) là góc nội tiếp chắn nửa đường tròn\(\Rightarrow A^{\prime} C=2 a\)
Đặt cạnh hình vuông là x. Khi đó:
\(\left\{\begin{array}{l} A^{\prime} D^{2}=A D^{2}-A^{\prime} A^{2}=x^{2}-a^{2} \\ A^{\prime} D^{2}+D C^{2}=A^{\prime} C^{2} \end{array} \Rightarrow 2 x^{2}-a^{2}=4 a^{2} \Rightarrow x^{2}=S_{A B C D}=\frac{5 a^{2}}{2}\right.\)
Giả sử \(\left(x_{0} ; y_{0}\right)\) là một nghiệm của phương trình\(4^{x-1}+2^{x} \sin \left(2^{x-1}+y-1\right)+2=2^{x}+2 \sin \left(2^{x-1}+y-1\right)\). Mệnh đề nào sau đây đúng?
Ta có:
\(4^{x-1}+2^{x} \sin \left(2^{x-1}+y-1\right)+2=2^{x}+2 \sin \left(2^{x-1}+y-1\right)\)
\(\begin{array}{l} \Leftrightarrow 4^{x}-4.2^{x}+4 .\left(2^{x}-2\right) \cdot \sin \left(2^{x-1}+y-1\right)+4+4=0 \\ \Leftrightarrow\left(2^{x}-2\right)^{2}+4\left(2^{x}-2\right) \sin \left(2^{x-1}+y-1\right)+4\left[\sin ^{2}\left(2^{x-1}+y-1\right)+\cos ^{2}\left(2^{x-1}+y-1\right)\right]=0 \\ \Leftrightarrow\left(2^{x}-2\right)^{2}+2 \cdot\left(2^{x}-2\right) \cdot 2 \sin \left(2^{x-1}+y-1\right)+\left[2 \sin ^{2}\left(2^{x-1}+y-1\right)\right]^{2}+4 \cos ^{2}\left(2^{x-1}+y-1\right)=0 \\ \Leftrightarrow\left[\left(2^{x}-2\right)+2 \sin \left(2^{x-1}+y-1\right)\right]^{2}+4 \cos ^{2}\left(2^{x-1}+y-1\right)=0 \\ \Leftrightarrow\left[\begin{array}{l} 2^{x}-2+2 \sin \left(2^{x-1}+y-1\right)=0 \\ \cos ^{2}\left(2^{x-1}+y-1\right)=0 \end{array}\right. \end{array}\)
Vì \(\cos ^{2}\left(2^{x-1}+y-1\right)=0 \Rightarrow \sin ^{2}\left(2^{x-1}+y-1\right)=\pm 1\)
\(\begin{array}{l} \sin ^{2}\left(2^{x-1}+y-1\right)=1 \Rightarrow 2^{x}=0 \text { (vô nghiệm) } \\ \sin ^{2}\left(2^{x-1}+y-1\right)=-1 \Rightarrow 2^{x}=4 \Rightarrow x=x_{0}=2 \in(-2 ; 4) \end{array}\)
Cho hình hộp \(A B C D \cdot A^{\prime} B^{\prime} C^{\prime} D'\) có các cạnh bằng 2a . Biết \(\widehat{B A D}=60^{\circ}, \widehat{A^{\prime} A B}=\widehat{A^{\prime} A D}=120^{\circ}\) Tính thể tích V của khối hộp \(A B C D \cdot A^{\prime} B^{\prime} C^{\prime} D^{\prime}\)
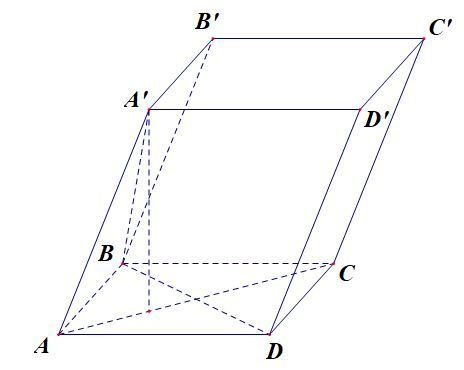
Từ giả thuyết ta có các tam giác \(\Delta A B D, \Delta A^{\prime} A D \text { và } A^{\prime} A B\)là các tam giác đều.
\(\Rightarrow A^{\prime} A=A^{\prime} B=A^{\prime} D\) nên hình chiếu H của A' trên mặt phẳng ( ABCD) là tâm đường tròn ngoại tiếp tam giác đều ABD .
\(\begin{array}{l} \Rightarrow A H=\frac{2}{3} .2 a \cdot \frac{\sqrt{3}}{2}=\frac{2 \sqrt{3}}{3} a \\ \Rightarrow A^{\prime} H=\sqrt{A^{\prime} A^{2}-A H^{2}}=\frac{2 \sqrt{6}}{3} a \end{array}\)
Thể tích khối hộp \(A B C D \cdot A^{\prime} B^{\prime} C^{\prime} D^{\prime}: \)
\(V=A^{\prime} H S_{A B C D}=\frac{2 \sqrt{6}}{3} a \cdot 2 \cdot \frac{4 a^{2} \cdot \sqrt{3}}{4}=4 \sqrt{2} a^{3}\)
Cho hàm số \(y=\left|x^{4}-2 x^{3}+x^{2}+a\right|\) . Có bao nhiêu số thực \(a \text { để } \min\limits _{[1 ; 2]} y+\max\limits _{[1 ; 2]} y=10 ?\)
Đặt \(y=\left|x^{4}-2 x^{3}+x^{2}+a\right|=|f(x)|\)
Xét hàm số \(f(x)=x^{4}-2 x^{3}+x^{2}+a\)
\(f^{\prime}(x)=4 x^{3}-6 x^{2}+2 x=2 x\left(2 x^{2}-3 x+1\right)=0 \Leftrightarrow x \in\left\{0 ; \frac{1}{2} ; 1\right\}\)
\(\Rightarrow f^{\prime}(x) \geq 0, \forall x \in[1 ; 2] \text { và } f(1)=a ; f(2)=a+4\)
ta có \(\forall x \in[1 ; 2] \text { thì }\left\{\begin{array}{l} \max y \in\{|a|,|a+4|\} \\ \min y \in\{|a|, 0,|a+4|\} \end{array}\right.\)
Xét các trường hợp:
\(a \geq 0 \Rightarrow \max y=a+4 ; \min y=a \Rightarrow 2 a+4=10 \Rightarrow a=3, \text {( nhận). }\)
\(a \leq-4 \Rightarrow \max y=-a ; \min y=-a-4 \Rightarrow-a-4-a=10 \Rightarrow a=-7 \text {( nhận) }\)
\(\left\{\begin{array}{l} a<0 \\ a+4>0 \end{array} \Leftrightarrow-4<a<0 \Rightarrow \min y=0 ; \max y \in\{a+4 ;-a\}\right.\)
\(\Rightarrow\left[\begin{array}{l} a+4=10 \\ -a=10 \end{array} \Rightarrow\left[\begin{array}{l} a=6 \\ a=-10 \end{array}\text { (Loại) }\right.\right.\)
Vậy tồn tại hai giá trị a thỏa mãn.
Cho hàm số y=f(x). Đồ thị hàm số y =f'(x) như hình vẽ. Cho bất phương trình \(3 f(x) \geq x^{3}-3 x+m\) (m là tham số thực). Điều kiện cần và đủ để bất phương trình \(3 f(x) \geq x^{3}-3 x+m\) đúng với mọi \(x \in[-\sqrt{3} ; \sqrt{3}]\) là:
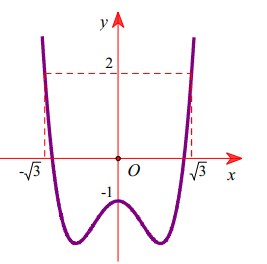
ta có: \(3 f(x) \geq x^{3}-3 x+m \Leftrightarrow 3 f(x)-x^{3}+3 x \geq m\)
Đặt \(g(x)=3 f(x)-x^{3}+3 x\)
\(g^{\prime}(x)=3 f^{\prime}(x)-3 x^{2}+3\)
\(g^{\prime}(x)=0 \Leftrightarrow f^{\prime}(x)=x^{2}-1\)
Nghiệm của phương trình \(g^{\prime}(x)=0\) là hoành độ giao điểm của đồ thị hàm số \(y=f^{\prime}(x)\) và parabol \(y=x^{2}-1\)
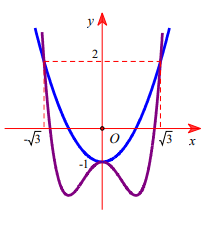
Dựa vào đồ thị hàm số :
\(f^{\prime}(x)=x^{2}-1 \Leftrightarrow\left[\begin{array}{l} x=-\sqrt{3} \\ x=0 \\ x=\sqrt{3} \end{array}\right.\)
Bảng biến thiên:
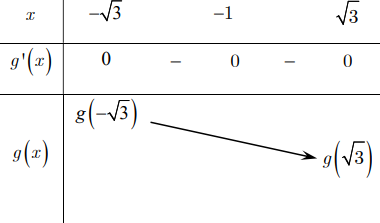
Để bất phương trình nghiệm đúng với mọi \(x \in[-\sqrt{3} ; \sqrt{3}]\)
thì \(m \leq \min\limits _{[-\sqrt{3} ; \sqrt{3}]} g(x)=g(\sqrt{3})=3 f(\sqrt{3})\)
Cho các số thực x y , thỏa mãn \(0 \leq x, y \leq 1 \text { và } \log _{3}\left(\frac{x+y}{1-x y}\right)+(x+1)(y+1)-2=0\). Tìm giá trị nhỏ nhất của P với \(P=2 x+y\)
Ta có:
\(\log _{3}\left(\frac{x+y}{1-x y}\right)+(x+1)(y+1)-2=0 \Leftrightarrow \log _{3}\left(\frac{x+y}{1-x y}\right)+x y+x+y-1=0\)
\(\Leftrightarrow \log _{3}(x+y)+x+y=\log _{3}(1-x y)+1-x y\)
Xét hàm đặc trưng \(f(t)=\log _{3} t+t \text { với } t>0\)
\(f^{\prime}(t)=\frac{1}{t \ln 3}+1>0, \forall t>0\)
suy ra hàm số f(t) đồng biến với \(t>0\)
Vậy:
\(f(x+y)=f(1-x y) \Leftrightarrow x+y=1-x y \Leftrightarrow x(y+1)=1-y \Leftrightarrow x=\frac{1-y}{y+1}\)
Ta có:
\(P=2 x+y=\frac{2-2 y}{y+1}+y=-3+\frac{4}{y+1}+y+1 \geq-3+2 \sqrt{\frac{4}{y+1}(y+1)}=1\)
Vậy giá trị nhỏ nhất của P bằng 1




