40 câu trắc nghiệm chuyên đề Mặt nón, mặt trụ, mặt cầu có lời giải ôn thi THPTQG năm 2019 -
40 câu trắc nghiệm chuyên đề Mặt nón, mặt trụ, mặt cầu có lời giải ôn thi THPTQG năm 2019 -
-
Hocon247
-
40 câu hỏi
-
90 phút
-
49 lượt thi
-
Trung bình
Tham gia [ Hs Hocon247.com ] - Cộng Đồng Luyện Thi Trực Tuyến để được học tập những kiến thức bổ ích từ HocOn247.com
Cho hình lập phương có cạnh bằng 40 cm và một hình trụ có hai đáy là hai hình tròn nội tiếp hai mặt đối diện của hình lập phương. Gọi \(S_1, S_2\) lần lượt là diện tích toàn phần của hình lập phương và diện tích toàn phần của hình trụ. Tính \(S=S_1+S_2\) \(cm^2\).
.png)
Ta có: \({S_1} = {6.40^2} = 9600\).
Bán kính đường tròn nội tiếp hai mặt đối diện của hình lập phương là: \(r = 20{\rm{ cm}}\); hình trụ có đường sinh \(h = 40{\rm{ cm}}\)
Diện tích toàn phần của hình trụ là: \({S_2} = 2.\pi {.20^2} + 2\pi .20.40 = 2400\pi \).
Vậy: \(S = {S_1} + S{}_2 = 9600 + 2400\pi = 2400\left( {4 + \pi } \right)\).
Cho tam giác SAB vuông tại A, \(\widehat {ABS} = 60^0 \), đường phân giác trong của \(\widehat {ABS}\) cắt SA tại điểm I. Vẽ nửa đường tròn tâm I bán kính IA ( như hình vẽ). Cho \(\Delta SAB\) và nửa đường tròn trên cùng quay quanh SA tạo nên các khối cầu và khối nón có thể tích tương ứng \(V_1, V_2\). Khẳng định nào dưới đây đúng?
Đặt \(AB = x \Rightarrow \left\{ \begin{array}{l}
IA = x\tan 30^0 \\
SA = x\tan 60^0
\end{array} \right.\).
Khối cầu: \({V_1} = \frac{4}{3}\pi {R^3} = \frac{4}{3}\pi I{A^3} = \frac{4}{3}\pi {\left( {x\tan 30^0} \right)^3}\).
Khối nón \({V_2} = \frac{1}{3}\pi A{B^2}SA = \frac{1}{3}\pi {x^2}.\left( {x\tan 60^0 } \right)\).
Vậy \(\frac{{{V_1}}}{{{V_2}}} = \frac{4}{9}\) hay \(9{V_1} = 4{V_2}\).
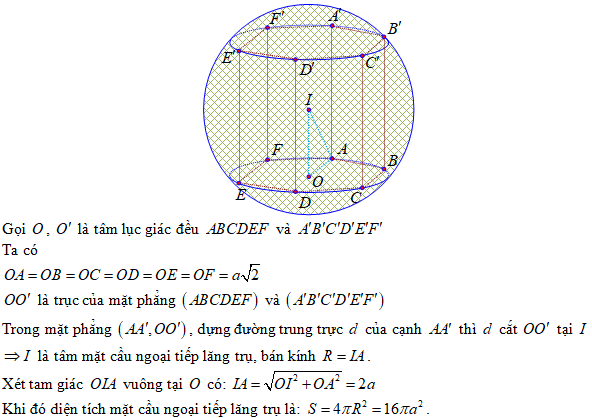
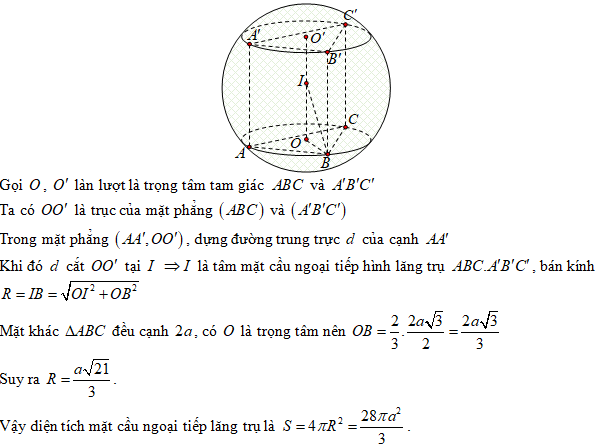
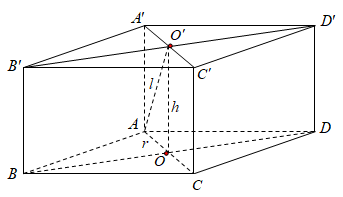
Cho lăng trụ tam giác đều có cạnh đáy bằng \(a\) cạnh bên bằng \(b\). Tính thể tích của khối cầu đi qua các đỉnh của lăng trụ.
Gọi \(I, I'\) lần lượt là tâm hai đáy, O là trung điểm của \(II'\). Khi đó ta có O là tâm mặt cầu ngoại tiếp lăng trụ.
Ta có: \(AI = \frac{{a\sqrt 3 }}{3},\,IO = \frac{b}{2}\) suy ra bán kính mặt cầu ngoại tiếp lăng trụ là \(R = \sqrt {\frac{{{a^2}}}{3} + \frac{{{b^2}}}{4}} = \frac{1}{{2\sqrt 3 }}\sqrt {4{a^2} + 3{b^2}} \)
Vậy \({V_{\left( {O;\,R} \right)}} = \frac{4}{3}\pi {R^3} = \frac{\pi }{{18\sqrt 3 }}\sqrt {{{\left( {4{a^2} + 3{b^2}} \right)}^3}} .\)
Cho hình trụ có thiết diện qua trục là hình vuông ABCD cạnh bằng \(2\sqrt 3 \,\left( {{\rm{cm}}} \right)\) với AB là đường kính của đường tròn đáy tâm O. Gọi M là điểm thuộc cung AB của đường tròn đáy sao cho \(\widehat {ABM} = 60^\circ \). Thể tích của khối tứ diện ACDM là:
Ta có: \(\Delta MAB\) vuông tại Mcó \(\widehat B = 60^0 \) nên \(MB = \sqrt 3 ;\)\(MA = 3\).
Gọi H là hình chiếu của M lên AB, suy ra \(MH \bot \left( {ACD} \right)\) và \(MH = \frac{{MB.MA}}{{AB}} = \frac{3}{2}.\)
Vậy \({V_{M.ACD}} = \frac{1}{3}MH.S{ _{ACD}} = \frac{1}{3}.\frac{3}{2}.6 = 3\,\left( {{\rm{c}}{{\rm{m}}^{\rm{3}}}} \right).\)
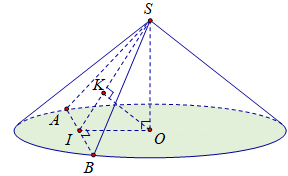
Cho hình nón tròn xoay có chiều cao \(h = 20\,\left( {{\rm{cm}}} \right)\), bán kính đáy \(r = 25\,\left( {{\rm{cm}}} \right)\). Một thiết diện đi qua đỉnh của hình nón có khoảng cách từ tâm đáy đến mặt phẳng chứa thiết diện là \(12\,\left( {{\rm{cm}}} \right)\). Tính diện tích của thiết diện đó.
Theo bài ra ta có \(AO = r = 25;SO = h = 20;\,OK = 12\) (Hình vẽ).
Lại có \(\frac{1}{{O{K^2}}} = \frac{1}{{O{I^2}}} + \frac{1}{{O{S^2}}} \Rightarrow OI = 15\,\left( {{\rm{cm}}} \right)\)
\(AB = 2AI = \sqrt {{{25}^2} - {{15}^2}} = 40\,\left( {{\rm{cm}}} \right);\;SI = \sqrt {S{O^2} + O{I^2}} = 25\,\left( {{\rm{cm}}} \right) \Rightarrow {S_{\Delta SAB}} = \frac{1}{2}.25.40 = 500\,\left( {{\rm{c}}{{\rm{m}}^2}} \right).\)
Cho hình trụ có hai đáy là hai hình tròn (O) và (O]), chiều cao \(R\sqrt 3 \) và bán kính đáy R. Một hình nón có đỉnh là O' và đáy là hình tròn (O;R). Tỷ số diện tích xung quanh của hình trụ và hình nón bằng
Ta có diện tích xung quanh của hình trụ là \({S_1} = 2\pi Rh = 2\pi R.R\sqrt 3 = 2\pi {R^2}\sqrt 3 .\)
Diện tích xung quanh của hình nón là \({S_2} = \pi Rl = \pi R.\sqrt {{{\left( {R\sqrt 3 } \right)}^2} + {R^2}} = 2\pi {R^2}.\)
Tỷ số diện tích xung quanh của hình trụ và hình nón bằng \(\frac{{{S_1}}}{{{S_2}}} = \frac{{2\pi {R^2}\sqrt 3 }}{{2\pi {R^2}}} = \sqrt 3 .\)
Cho hình thang ABCD vuông tại A và B với \(AB = BC = \frac{{AD}}{2} = a\) . Quay hình thang và miền trong của nó quanh đường thẳng chứa cạnh BC. Tính thể tích V của khối tròn xoay được tạo thành
Gọi \(V_1\) là thể tích khối nón có đường sinh là CD , bán kính \(R=AB=a\), chiều cao \(h=a\)
\({V_1} = \frac{1}{3}\pi {R^2}h = \frac{1}{3}\pi {a^2}.a = \frac{{{a^3}}}{3}\pi \).
Gọi \(V_2\) là thể tích khối trụ có đường sinh là \(AD=2a\) , bán kính \(R = AB = a\), chiều cao \(h'=2a\).
\({V_2} = \pi {R^2}h' = \pi .{a^2}.2a = 2{a^3}\pi \) .
Thể tích V của khối tròn xoay được tạo thành là : \(V = {V_2} - {V_1} = 2{a^3}\pi - \frac{{{a^3}\pi }}{3} = \frac{{5{a^3}\pi }}{3}\) .
Cho hình tứ diện ABCD có M, N lần lượt là trung điểm của AB, BD. Các điểm G, H lần lượt trên cạnh AC, CD sao cho NH cắt MG tại I. Khẳng định nào sau đây là khẳng định đúng?
Do NH cắt MG tại I nên bốn điểm M, N, H, G cùng thuộc mặt phẳng \(\left( \alpha \right)\). Xét ba mặt phẳng (ABC), (BCD), \(\left( \alpha \right)\) phân biệt, đồng thời \(\left\{ \begin{array}{l}
\left( \alpha \right) \cap \left( {ABC} \right) = MG\\
\left( \alpha \right) \cap \left( {BCD} \right) = NH\\
\left( {ABC} \right) \cap \left( {BCD} \right) = BC
\end{array} \right.\) mà \(MG \cap NH = I\)
Suy ra MG, NB, BC đồng quy tại I nên B, C, I thẳng hàng.
Hình nón có thiết diện qua trục là tam giác đều và có thể tích \(V = \frac{{\sqrt 3 }}{3}\pi {a^3}\). Diện tích xung quanh S của hình nón đó là
Vì thiết diện là tam giác đều nên \(l=2r\) và \(h = r\sqrt 3 \)
Ta có \(V = \frac{{\sqrt 3 }}{3}\pi {a^3} \Leftrightarrow \frac{1}{3}\pi {r^2}h = \frac{{\sqrt 3 }}{3}\pi {a^3} \Leftrightarrow r = a \Rightarrow l = 2a\)
Vậy \(S = \pi rl = 2\pi {a^2}\).
Cho một khối nón có chiều cao bằng 4cm, độ dài đường sinh 5cm. Tính thể tích khối nón này.

Theo giả thiết ta có: \(h = SO = 4cm,l = SB = 5cm \Rightarrow R = 3cm\).
Vậy thể tích khối nón cần tìm là : \({V_{n\'o n}} = \frac{1}{3}h.\pi {R^2} = 12\pi c{m^3}\).
Cho hình lập phương ABCD.A'B'C'D' cạnh bằng \(3a\). Quay đường tròn ngoại tiếp tam giác A'BD quanh một đường kính của đường tròn ta có một mặt cầu, tính diện tích mặt cầu đó.

Tam giác A'BD là tam giác đều, cạnh bằng \(3a\sqrt 2 \).
Quay đường tròn ngoại tiếp tam giác A'BD quanh một đường kính của đường tròn, ta được mặt cầu có bán kính bằng: \(\frac{{\sqrt 3 }}{3}.3a\sqrt 2 = a\sqrt 6 \).
Diện tích mặt cầu được tạo ra: \(S = 4\pi {R^2} = 4\pi .6{a^2} = 24\pi {a^2}\).
Một hình nón có đường sinh bằng \(a\) và góc ở đỉnh bằng \(90^0\). Cắt hình nón bằng một mặp phẳng \(\left( \alpha \right)\) sao cho góc giữa \(\left( \alpha \right)\) và mặt đáy hình nón bằng \(60^0\). Khi đó diện tích thiết diện là

Gọi S là đỉnh hình nón, O là tâm đường tròn đáy; I là trung điểm AB, Góc tạo bởi mp thiết diện và đáy là góc \(\widehat {SIO}\)
+ Trong tam giác vuông SOA có \(OA = OS = \frac{{a\sqrt 2 }}{2}\);
+ Trong tam giác vuông SOI có \(SI = \frac{{SO}}{{\sin 60^\circ }} = \frac{{a\sqrt 2 }}{{\sqrt 3 }}\); \(OI = \frac{{SO}}{{\tan 60^\circ }} = \frac{{a\sqrt 6 }}{6}\);
\(AI = \sqrt {O{A^2} - O{I^2}} = \frac{a}{{\sqrt 3 }};AB = \frac{{2a}}{{\sqrt 3 }}\)
\({S_{td}} = \frac{1}{2}AB.SI = \frac{{\sqrt 2 {a^2}}}{3}\).
Cho một khối trụ có độ dài đường sinh bằng 10 cm. Biết thể tích khối trụ bằng \(90\pi {\rm{ c}}{{\rm{m}}^3}\). Tính diện tích xung quanh của khối trụ.
Ta có: \(h = l = 10{\rm{ cm}}\)
\(V = 90\pi \Leftrightarrow \pi {r^2}.h = 90\pi \Leftrightarrow {r^2} = 9 \Leftrightarrow r = 3{\rm{ cm}}\)
Vậy \({S_{xq}} = 2\pi rl = 60\pi {\rm{ c}}{{\rm{m}}^2}\)
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng \(a\). Một hình nón có đỉnh là tâm hình vuông A'B'C'D' và có đường tròn đáy ngoại tiếp hình vuông ABCD. Gọi S là diện tích xung quanh của hình nón đó. Tính S.
Ta có \(r = \frac{{AC}}{2} = \frac{{a\sqrt 2 }}{2},h = OO' = AA' = a,l = \sqrt {{h^2} + {r^2}} = \sqrt {{a^2} + \frac{{{a^2}}}{2}} = \frac{{a\sqrt 6 }}{2}\)
\(S = \pi rl = \pi .\frac{{a\sqrt 2 }}{2}.\frac{{a\sqrt 6 }}{2} = \pi \frac{{\sqrt 3 }}{2}{a^2}\)
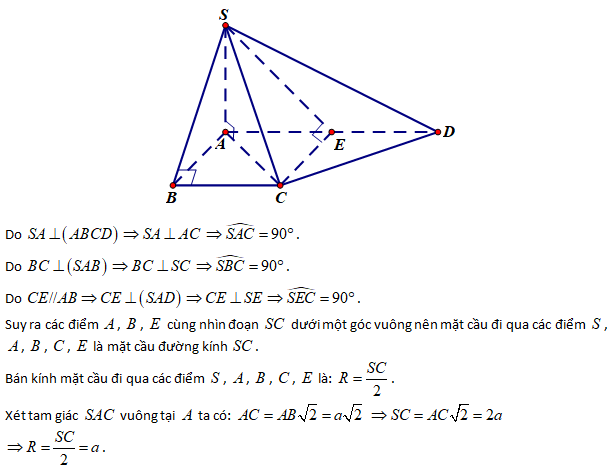
Cho hình chóp S.ABCD có đáy là hình chữ nhật, SA vuông góc với đáy, \(SA=a, AD = 5a,\;AB = 2a.\) Điểm E thuộc cạnh BC sao cho \(CE=a\). Tính theo \(a\) bán kính mặt cầu ngoại tiếp tứ diện S.AED.

Ta có \(A{E^2} = A{B^2} + B{E^2} = 4{a^2} + {\left( {4a} \right)^2} = 20{a^2},D{E^2} = D{C^2} + C{E^2} = 4{a^2} + {a^2} = 5{a^2}.\)
Do đó \(A{E^2} + D{E^2} = A{D^2} = 25{a^2}\), suy ra tam giác AED suy ra tam giác AED vuông ở
E. Suy ra \(ED \bot \left( {SAE} \right) \Rightarrow ED \bot SE\). Vậy A và E đều nhìn SD dưới một góc vuông. Do đó mặt cầu ngoại tiếp tứ diện SAED có bán kính là \(R = \frac{{SD}}{2} = \frac{1}{2}\sqrt {S{A^2} + A{D^2}} = \frac{{a\sqrt {26} }}{2}.\)
Cho mặt cầu \((S_1)\) có bán kính \(R_1\), mặt cầu \((S_2)\) có bán kính \(R_2=2R_1\). Tính tỉ số diện tích của mặt cầu \((S_2)\) và \((S_1)\).
\({S_{\left( {{S_1}} \right)}} = 4\pi R_1^2;{S_{\left( {{S_2}} \right)}} = 4\pi R_{_2}^2 = 16\pi R_{_1}^2\)
Vậy \(\frac{{{S_{\left( {{S_2}} \right)}}}}{{{S_{\left( {{S_1}} \right)}}}} = 4\)
Cho tứ diện đều S.ABC cạnh \(a\). Diện tích xung quanh của hình nón đỉnh S và đường tròn đáy là đường tròn ngoại tiếp tam giác ABC là

\(r = AO = \frac{{a\sqrt 3 }}{3}\)
\({S_{xq}} = \pi rl = \pi r.SA = \frac{{\pi \sqrt 3 }}{3}{a^2}\)
Cho hình chóp S.ABC có tam giác ABC vuông tại B, SA vuông góc với mặt phẳng (ABC). \(SA=5, AB=3, BC=4\). Tính bán kính R của mặt cầu ngoại tiếp hình chóp S.ABC.
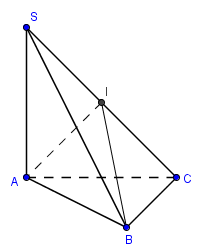
Ta có \(BC \bot SA\) và \(BC \bot AB\) nên \(BC \bot \left( {SAB} \right) \Rightarrow BC \bot SB.\) Vậy hai điểm A, B cùng nhìn cạnh SC dưới một góc vuông. Điều đó chứng tỏ SC là đường kính của mặt cầu ngoại tiếp hình chóp S.ABC. Do đó bán kính
\(R = \frac{{SC}}{2} = \frac{1}{2}\sqrt {S{A^2} + A{C^2}} = \frac{1}{2}\sqrt {S{A^2} + A{B^2} + B{C^2}} = \frac{1}{2}\sqrt {{5^2} + {3^2} + {4^2}} = \frac{{5\sqrt 2 }}{2}.\)
Một hình trụ có bán kính đáy là 2 cm. Một mặt phẳng đi qua trục của hình trụ, cắt hình trụ theo thiết diện là một hình vuông. Tính thể tích khối trụ đó.
Giả sử ABCD là thiết diện qua trục của hình trụ (hình vẽ). Theo giả thiết ABCD là hình vuông nên chiều cao của hình trụ \(h = OO' = 2r = 4\,\left( {{\rm{cm}}} \right)\).
Vậy thể tích khối trụ \(V = \pi {r^2}h = \pi {.2^2}.4 = 16\pi \,\left( {{\rm{c}}{{\rm{m}}^{\rm{3}}}} \right)\).
Cho hình trụ (T) được sinh ra khi quay hình chữ nhật ABCD quanh cạnh AB. Biết \(AC = 2\sqrt 3 a\) và góc \(\widehat {ACB} = 45^\circ \). Diện tích toàn phần \(S_{tp}\) của hình trụ (T) là
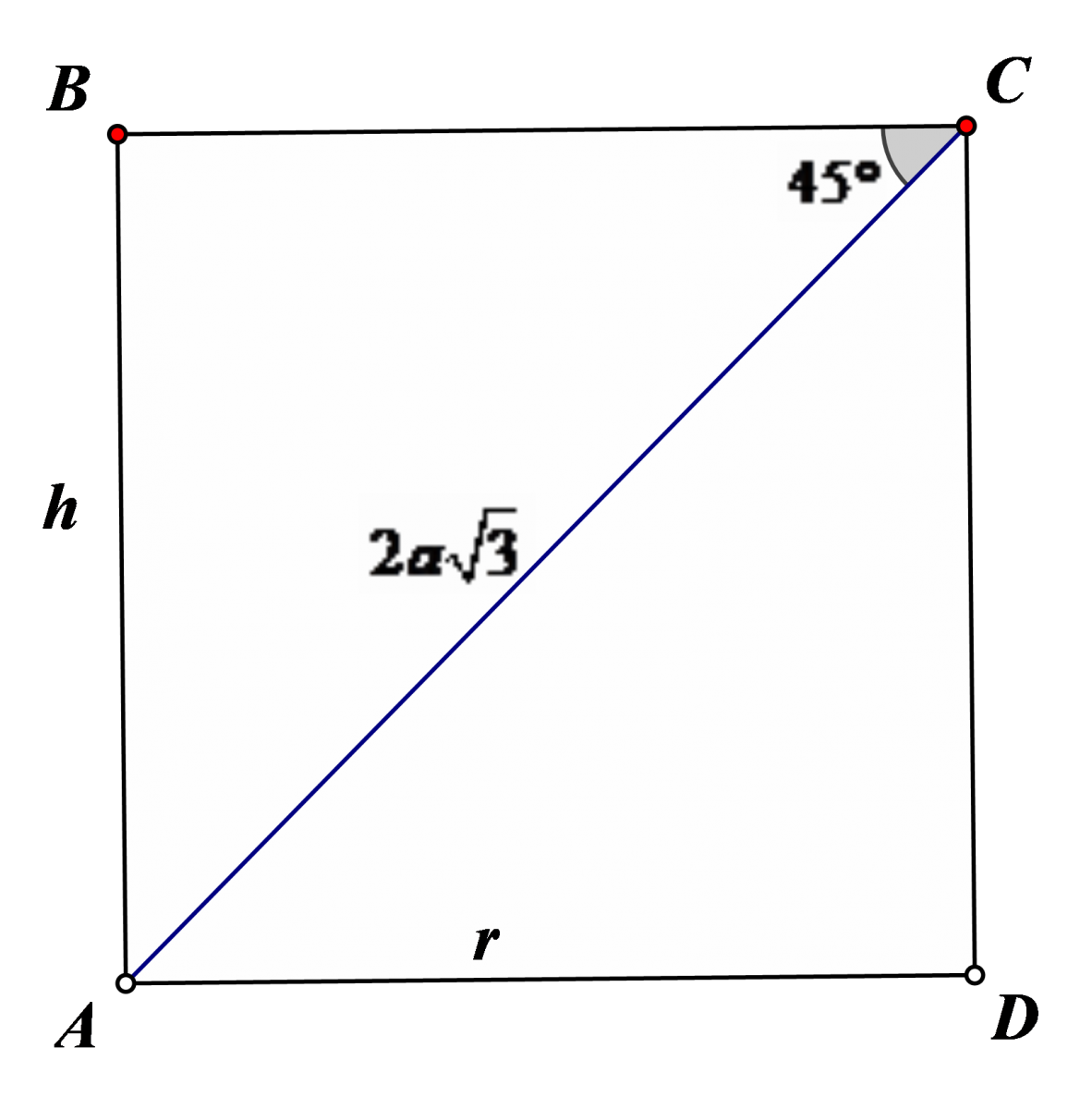
Theo đề bài suy ra ABCD là hình vuông và \(AB = \frac{{AC}}{{\sqrt 2 }} = a\sqrt 6 \).
Hình trụ sinh ra có bán kính \(r = AD = a\sqrt 6 \) và độ dài đường sinh \(l = CD = a\sqrt 6 \).
Vậy diện tích toàn phần của hình trụ là \({S_{tp}} = {S_{xq}} + 2{S_d} = 2\pi {\left( {a\sqrt 6 } \right)^2} + 2\pi {\left( {a\sqrt 6 } \right)^2} = 24\pi {a^2}\).
Thể tích của khối nón có độ dài đường sinh bằng \(2a\) và diện tích xung quanh bằng \(2\pi {a^2}\) là
Gọi \(R, h, l\) lần lượt là bán kính đáy, độ dài đường sinh, chiều cao của hình nón.
\(\begin{array}{l}
{S_{xq}} = 2\pi {a^2} \Leftrightarrow \pi Rl = 2\pi {a^2} \Leftrightarrow Rl = 2{a^2} \Leftrightarrow R = \frac{{2{a^2}}}{l} = \frac{{2{a^2}}}{{2a}} = a\\
h = \sqrt {{l^2} - {R^2}} = \sqrt {4{a^2} - {a^2}} = a\sqrt 3 \\
V = \frac{1}{3}\pi {R^2}h \Leftrightarrow V = \frac{1}{3}\pi {a^2}a\sqrt 3 = \frac{{\sqrt 3 }}{3}\pi {a^3}.
\end{array}\)
Cắt một hình trụ bởi một mặt phẳng qua trục của nó, ta được thiết diện là một hình vuông có cạnh bằng \(3a\). Tính diện tích toàn phần của hình trụ đã cho.
Do mặt phẳng cắt hình trụ đi qua trục của nó nên ta có:
Đường sinh \(l=3a\) và bán kính đáy \(r = \frac{{3a}}{2}\).
Vậy diện tích toàn phần của hình trụ: \({S_{tp}} = 2\pi r\left( {r + l} \right) = \frac{{27\pi {a^2}}}{2}\).
Cho tam giác ABC vuông tại A, \(AB=6cm, AC=8cm\). Gọi \(V_1\) là thể tích khối nón tạo thành khi quay tam giác ABC quanh cạnh AB và \(V_2\) là thể tích khối nón tạo thành khi quay tam giác ABC quanh cạnh AC. Khi đó, tỷ số \(\frac{{{V_1}}}{{{V_2}}}\) bằng:
Khi quay tam giác ABC quanh cạnh AB ta có:
\(h = AB,r = AC \Rightarrow {V_1} = \frac{1}{3}\pi .{r^2}.h = \frac{1}{3}\pi {.8^2}.6 = 128\pi \,\left( {{\rm{c}}{{\rm{m}}^{\rm{3}}}} \right)\).
Khi quay tam giác ABC quanh cạnh AC ta có:
\(h = AC,r = AB \Rightarrow {V_2} = \frac{1}{3}\pi .{r^2}.h = \frac{1}{3}\pi {.6^2}.8 = 96\pi \,\left( {{\rm{c}}{{\rm{m}}^{\rm{3}}}} \right)\).
Vậy \(\frac{{{V_1}}}{{{V_2}}} = \frac{{128}}{{96}} = \frac{4}{3}\).
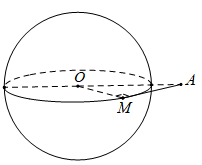
Cho mặt cầu \(S(O;R)\) và điểm A cố định nằm ngoài mặt cầu với \(OA=d\). Qua A kẻ đường thẳng \(\Delta \) tiếp xúc với mặt cầu \(S\left( {O;R} \right)\) tại M. Công thức nào sau đây được dùng để tính độ dài đoạn thẳng AM?
Vì \(\Delta \) tiếp xúc với mặt cầu \(S\left( {O;R} \right)\) tại M nên \(\Delta \) tiếp xúc với một đường tròn lớn của mặt cầu \(S\left( {O;R} \right)\) tại M. Do đó \(\Delta OMA\) vuông tại M, suy ra \(AM = \sqrt {O{A^2} - O{M^2}} = \sqrt {{d^2} - {R^2}} \).
Trong không gian, cho hình chữ nhật ABCD có AB = 1 và AD = 2. Gọi M, N lần lượt là trung điểm của AD và BC. Quay hình chữ nhật đó xung quanh trục MN, ta được một hình trụ. Tính diện tích toàn phần \(S_{tp}\) của hình trụ đó.
.png)
Ta có \({S_{xq}} = 2\pi rl = 2.\pi .1.1 = 2\pi \)
\({S_d} = 2.\pi .{r^2} = 2.\pi .1 = 2\pi \)
Suy ra \({S_{tp}} = {S_{sq}} + {S_d} = 2\pi + 2\pi = 4\pi \)
Cho hình nón có đường sinh bằng đường kính đáy và bằng 2. Bán kính của mặt cầu ngoại tiếp hình nón đó là:
Gọi các điểm như hình vẽ bên.
Trong đó H là tâm đường tròn đáy (C) suy ra \(SH \bot \left( C \right)\), và \(HA=1\).
Điểm I là tâm mặt cầu ngoại tiếp hình nón (N).
Trong tam giác vuông IHA ta có \(IH = \sqrt {{R^2} - 1} \).
Khi đó: \(SH = SI + IH = R + \sqrt {{R^2} - 1} = \sqrt 3 \Leftrightarrow \left\{ \begin{array}{l}
\sqrt 3 - R > 0\\
{R^2} - 1 = {R^2} - 2\sqrt 3 R + 3
\end{array} \right.\) \( \Leftrightarrow R = \frac{{2\sqrt 3 }}{3}\).
Cho tam giác ABC có \(\widehat {ABC} = 45^\circ \widehat {,ACB} = 30^\circ ,AB = \frac{{\sqrt 2 }}{2}\). Quay tam giác ABC xung quanh cạnh BC ta được khối tròn xoay có thể tích V bằng:
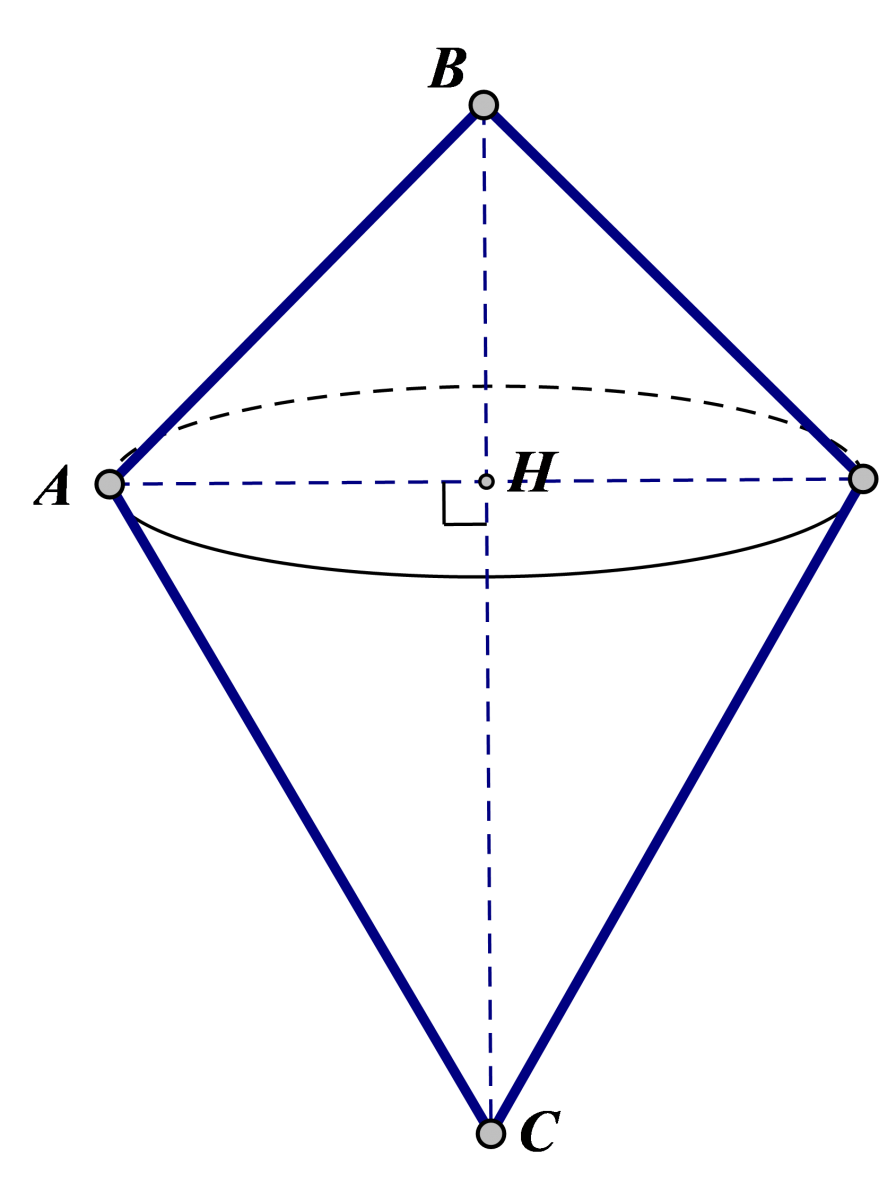
Ta có \(\frac{{AB}}{{\sin 30^\circ }} = \frac{{AC}}{{\sin 45^\circ }} = \frac{{BC}}{{\sin 105^\circ }} \Rightarrow \left\{ \begin{array}{l}
AC = 1\\
BC = \sqrt 2 \sin \frac{{5\pi }}{{12}} = \frac{{1 + \sqrt 3 }}{2}
\end{array} \right.\).
Gọi H là chân đường cao kẻ từ đỉnh A. Ta \(AH.BC = AB.AC.\sin 105^0 \Rightarrow AH = \frac{1}{2}\).
Suy ra thể tích khối tròn xoay cần tìm là \(V = \frac{1}{3}\pi .A{H^2}.BC = \frac{{\pi \left( {1 + \sqrt 3 } \right)}}{{24}}\).
Cắt khối trụ bởi một mặt phẳng qua trục ta được thiết diện là hình chữ nhật có và thuộc hai đáy của hình trụ, \(AB = 4a,AC = 5a\). Tính thể tích khối trụ.

Ta có
+ Bán kính đường tròn đáy là: \(r = \frac{{AB}}{2} = 2a\).
+ Chiều cao khối trụ: \(h = AD = \sqrt {A{C^2} - C{D^2}} = \sqrt {{{\left( {5a} \right)}^2} - {{\left( {4a} \right)}^2}} = 3a\).
+ Thể tích khối trụ: \(V = \pi .{r^2}.h = \pi .{(2a)^2}.3a = 12\pi {a^3}\).
Cho mặt cầu bán kính R ngoại tiếp một hình hộp chữ nhật có các kích thước \(a, 2a, 3a\). Mệnh đề nào dưới đây đúng?
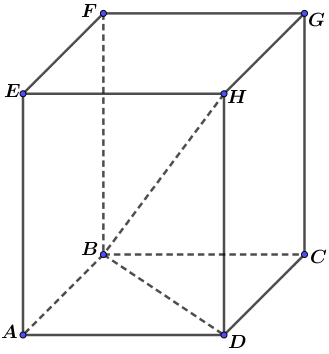
Gọi hình hộp chữ nhật đã cho là ABCD.EFGH. Mặt cầu bán kính ngoại tiếp hình hộp chữ nhật ABCD.EFGH nhận đường chéo BH là đường kính.
Do đó bán kính \(R = \frac{{BH}}{2} = \frac{1}{2}\sqrt {{a^2} + 4{a^2} + 9{a^2}} = \frac{{a\sqrt {14} }}{2} \Rightarrow a = \frac{{2R}}{{\sqrt {14} }} = \frac{{R\sqrt {14} }}{7}\).
Tam giác ABC vuông cân đỉnh A có cạnh huyền là 2. Quay tam giác ABC quanh trục BC thì được khối tròn xoay có thể tích là
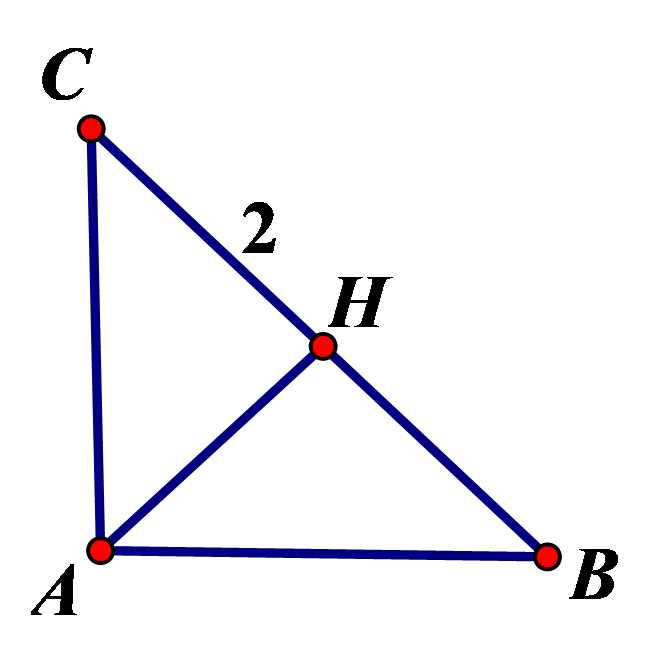
Ta có: \(AB = AC = \sqrt 2 \).
Gọi H là trung điểm của cạnh AB thì \(AH \bot BC\) và AH = 1.
Quay tam giác ABC quanh trục BC thì được khối tròn xoay có thể tích là
\(V = 2.\frac{1}{3}HB.\pi A{H^2} = \frac{{2\pi }}{3}\)
Cho hình chóp S.ABCD có đáy là hình vuông, \(BD=2a\). Tam giác SAC vuông cân tạiÁC và nằm trong mặt phẳng vuông góc với đáy. Thể tích của khối cầu ngoại tiếp hình chóp đó là
Vì tam giác SAC vuông cân tại S \( \Rightarrow OS = OA = OC\) (1).
Mặt khác ta có đáy ABCD là hình vuông \( \Rightarrow OA = OC = OB = OD = \frac{{BD}}{2} = a\) (2).
Từ (1) và (2), suy ra O là tâm mặt cầu ngoại tiếp chóp S.ABCD. Do đó \(R = OA = a\).
Thể tích khối cầu: \(V = \frac{4}{3}\pi {R^3} = \frac{4}{3}\pi {a^3}\).
Cho hình nón đỉnh S, đáy là hình tròn tâm O, bán kính, \(R=3cm\), góc ở đỉnh hình nón là \(\varphi = 120^0 \). Cắt hình nón bởi mặt phẳng qua đỉnh S tạo thành tam giác đều SAB, trong đó A, B thuộc đường tròn đáy. Diện tích tam giác SAB bằng

Theo đề bài ta có góc ở đỉnh hình nón là \(\varphi = 120^0 \) và khi cắt hình nón bởi mặt phẳng qua đỉnh S tạo thành tam giác đều SAB nên mặt phẳng không chứa trục của hình nón.
Do góc ở đỉnh hình nón là \(\varphi = 120^0 \) nên \(\widehat {OSC} = 60^0 \).
Xét tam giác vuông SOC ta có \(\tan \widehat {OSC} = \frac{{OC}}{{SO}} \Rightarrow SO = \frac{{OC}}{{\tan \widehat {OSC}}} = \frac{3}{{\tan 60^\circ }} = \sqrt 3 \).
Xét tam giác vuông SAO ta có \(SA = \sqrt {S{O^2} + O{A^2}} = 2\sqrt 3 \)
Do tam giác SAB đều nên \({S_{\Delta SAB}} = \frac{1}{2}{\left( {2\sqrt 3 } \right)^2}.\sin 60^0 = 3\sqrt 3 \left( {{\rm{c}}{{\rm{m}}^{\rm{2}}}} \right)\).
Cho hình chóp tam giác đều S.ABC. Hình nón có đỉnh S và có đường tròn đáy là đường tròn nội tiếp tam giác ABC gọi là hình nón nội tiếp hình chóp S.ABC, hình nón có đỉnh S và có đường tròn đáy là đường tròn ngoại tiếp tam giác ABC gọi là hình nón ngoại tiếp hình chóp S.ABC. Tỉ số thể tích của hình nón nội tiếp và hình nón ngoại tiếp hình chóp đã cho là

Gọi M là trung điểm của BC.
Gọi O là trọng tâm của tam giác ABC.
Ta có: \(SO \bot \left( {ABC} \right)\) tại O.
Suy ra, Ô là tâm đường tròn nội tiếp và cũng là tâm của đường tròn ngoại tiếp tam giác ABC.
Gọi \(a\) là độ dài cạnh của tam giác ABC.
Gọi \(V_1, V_2\) lần lượt là thể tích của hình nón nội tiếp và hình nón ngoại tiếp hình chóp S.ABC.
Do \(OM = \frac{1}{2}OA\) nên ta có: \(\frac{{{V_1}}}{{{V_2}}} = \frac{{\frac{1}{3}.\pi .O{M^2}.SO}}{{\frac{1}{3}.\pi .O{A^2}.SO}} = \frac{{O{M^2}}}{{O{A^2}}} = {\left( {\frac{{OM}}{{OA}}} \right)^2} = {\left( {\frac{1}{2}} \right)^2} = \frac{1}{4}\).
Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng \(a\). Cạnh bên SA vuông góc với mặt đáy và \(SA = a\sqrt 2 \). Tính thể tích khối cầu ngoại tiếp hình chóp S.ABCD theo \(a\).

Ta chứng minh được các tam giác SBC, SAC và SCD là các tam giác vuông lần lượt tại B, A, D.
Suy ra các điểm B, A, D nhìn cạnh SC dưới một góc vuông.
Gọi I là trung điểm SC \( \Rightarrow I\) là tâm mặt cầu ngoại tiếp hình chóp S.ABCD.
Khi đó bán kính mặt cầu ngoại tiếp hình chóp S.ABCD là:
\(R = AI = \frac{1}{2}\sqrt {S{A^2} + A{C^2}} = \frac{1}{2}\sqrt {{{\left( {a\sqrt 2 } \right)}^2} + {{\left( {a\sqrt 2 } \right)}^2}} = a\).
Vậy thể tích khối cầu ngoại tiếp hình chóp S.ABCD là: \(V = \frac{4}{3}\pi {R^3} = \frac{4}{3}\pi .{a^3} = \frac{{4\pi {a^3}}}{3}\).
Một cái nồi nấu nước người ta làm dạng hình trụ, chiều cao của nồi là 60cm, diện tích đáy \(900\pi cm^2\). Hỏi người ta cần miếng kim loại hình chữ nhật có kích thước là bao nhiêu để làm thân nồi đó? (bỏ qua kích thước các mép gấp).
Gọi R là bán kính mặt đáy. Ta có: \({S_d} = \pi {R^2} \Rightarrow 900\pi = \pi {R^2} \Leftrightarrow {R^2} = 900 \Leftrightarrow R = 30\).
Suy ra chu vi đáy là \(2\pi R = 60\pi \).
Vậy cần miếng kim loại hình chữ nhật có chiều dài \(60\ pi\) cm, chiều rộng 60 cm để làm thân nồi đó.

.PNG)
.PNG)

.PNG)
.PNG)
.PNG)
.PNG)