Đề thi thử THPT QG năm 2021 môn Vật Lý - Trường THPT Chuyên Lê Thánh Tông - Quảng Nam
Đề thi thử THPT QG năm 2021 môn Vật Lý
-
Hocon247
-
40 câu hỏi
-
90 phút
-
60 lượt thi
-
Dễ
Tham gia [ Hs Hocon247.com ] - Cộng Đồng Luyện Thi Trực Tuyến để được học tập những kiến thức bổ ích từ HocOn247.com
Một sóng ngang có biểu thức truyền sóng trên phương x là u=3cos(100πt-x)cm, trong đó x tính bằng mét, t tính bằng giây. Tần số của sóng là
Phương trình sóng: \(u=3\cos (100\pi t-x)(cm)\)
Từ phương trình ta có: \(\omega =100\pi (ra\text{d/s)}\)
\(\Rightarrow \) Tần số của sóng: \(\frac{100\pi }{2\pi }=50\text{Hz}\)
Âm do một chiếc đàn bầu phát ra
Âm do một chiếc đàn bầu phát ra:
- Nghe càng trầm khi tần số nhỏ, nghe càng cao khi tần số lớn.
- Độ cao phụ thuộc vào tần số âm.
- Âm sắc phụ thuộc vào dạng đồ thị dao động của âm.
Một con lắc đơn có chiều dài l = 1m được gắn vào vật m. Cho vật dao động điều hòa tại nơi có gia tốc trọng trường là g = 10 = π2 (m/s2). Tần số dao động của con lắc là
Tần số dao động của con lắc đơn: \(\frac{1}{2\pi }\sqrt{\frac{10}{1}}=0,5Hz\) \(f=\frac{1}{2\pi }\sqrt{\frac{g}{l}}=\)
Khi một vật dao động điều hòa thì
A – sai vì gia tốc của vật có độ lớn cực đại tại vị trí biên.
B – sai vì lực kéo về có độ lớn tỉ lệ với li độ dao động của vật.
C – sai vì lực kéo về có độ lớn cực đại tại biên.
D – đúng.
Hai nguồn sóng kết hợp A, B cùng biên độ a, cùng pha, bước sóng \(\lambda \). Khoảng cách từ trung điểm O của AB đến điểm cực tiểu giao thoa gần nhất trên AB là
Do A, B là hai nguồn có cùng biên độ, cùng pha \(\Rightarrow \) Trung điểm O của AB là cực đại
Khoảng cách từ O đến điểm cực tiểu giao thoa gần nhất trên AB là \(\frac{\lambda }{4}\)
Một con lắc đơn có chiều dài l được kích thích dao động tại nơi có gia tốc trọng trường là g và con lắc dao động với chu kì T. Hỏi nếu giảm chiều dài dây treo đi một nửa thì chu kì của con lắc sẽ thay đổi như thế nào?
+ Khi chiều dài con lắc là l: \(T=2\pi \sqrt{\frac{l}{g}}\)
+ Khi chiều dài con lắc là \(\frac{l}{2}:{T}'=2\pi \sqrt{\frac{\frac{l}{2}}{g}}=\frac{T}{\sqrt{2}}\)
\(\Rightarrow \) Chiều dài của con lắc khi này giảm 2 lần.
Trong một đoạn mạch điện xoay chiều chỉ có tụ điện thì hiệu điện thế ở hai đầu đoạn mạch
Mạch điện xoay chiều chỉ có tụ điện khi đó hiệu điện thế ở hai đầu đoạn mạch trễ pha \(\frac{\pi }{2}\) so với cường độ dòng điện.
Mạch chỉ có R, biểu thức i qua mạch có dạng i = 2cos100πt(A), R = 20Ω. Viết biểu thức u?
Mạch chỉ có điện trở \({{U}_{0}}={{I}_{0}}R=2.20=40\text{V}\)
Và: \({{\varphi }_{u}}={{\varphi }_{i}}=0\)
\(\Rightarrow \) Biểu thức của điện áp: \(u=40\cos (100\pi t)V\)
Một người có điểm cực viễn cách mắt 1m. Người này phải đeo sát mắt kính có độ tụ bao nhiêu để nhìn vật ở xa vô cùng mà không điều tiết?
Ta có: \({d}'=O{{C}_{V}}=-1m,d=\infty \)
Độ tu: \(D=\frac{1}{f}=\frac{1}{d}+\frac{1}{O{{C}_{V}}}=\frac{1}{\infty }+\frac{1}{-1}=-1dp\)
Một sóng truyền theo phương AB. Tại một thời điểm nào đó, hình dạng sóng có dạng như hình vẽ. Biết rằng điểm M đang đi lên vị trí cân bằng. Khi đó, điểm N đang chuyển động như thế nào?
.png)
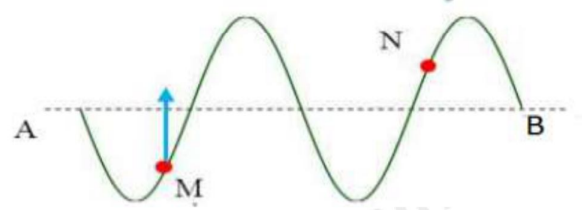
Theo phương truyền sóng, các phần tử trước đỉnh sóng sẽ đi xuống, sau đỉnh sóng sẽ đi lên.
Từ đồ thị ta có, điểm M sau đỉnh sóng đang đi lên.
\(\Rightarrow \) Sóng truyền từ B đến A và N cũng đang đi lên.
Mạch điện có R mắc vào mạng điện một chiều có giá trị suất điện động là U0 thì công suất tiêu thụ điện của mạch là P0. Khi mạch trên được mắc vào mạng điện xoay chiều có \(u={{U}_{0}}\cos (100\pi t)V\)thì công suất của mạch là P. Xác định tỉ số \(\frac{{{\text{P}}_{\text{0}}}}{\text{P}}\)
+ Trong mạch điện 1 chiều, công suất tiêu thụ của mạch: \({{P}_{0}}=\frac{U_{0}^{2}}{R}\)
+ Trong mạch điện xoay chiều, công suất tiêu thụ của mạch: \(P=\frac{{{U}^{2}}}{R}=\frac{U_{0}^{2}}{2R}\)
\(\Rightarrow \frac{{{P}_{0}}}{P}=2\)
Đặc điểm nào sau đây đúng với nhạc âm?
Nhạc âm có đồ thị dao động âm là những đường tuần hoàn có tần số xác định.
Khi nói về sự phản xạ của sóng cơ trên vật cản cố định, câu nào sau đây là đúng?
A – sai: Tần số của 2 sóng là như nhau.
B – sai: Sóng phản xạ luôn ngược pha với sóng tới ở điểm phản xạ.
C – đúng.
D – sai.
Một chất điểm dao động theo phương trình x = 6cos\(\omega \)t(cm). Dao động của chất điểm có độ dài quỹ đạo là
Chiều dài quỹ đạo: L = 2A = 2.6 =12cm
Một vật dao động điều hòa với chu kì T. Chọn gốc thời gian là lúc vật qua vị trí cân bằng, vận tốc của vật bằng 0 lần đầu tiên ở thời điểm
.png)
Vận tốc của vật bằng 0 lần đầu tiên ở thời điểm \(t=\frac{T}{4}\)
Một vật nhỏ khối lượng 100g dao động theo phương trình x = 8cos10t (x tính bằng cm, t tính bằng s). Động năng cực đại của vật bằng
Động năng cực đại của vật:
\({{\text{W}}_{{{d}_{\max }}}}=\frac{1}{2}mv_{\max }^{2}=\frac{1}{2}m{{(A\omega )}^{2}}=\frac{1}{2}\cdot 0,1.{{(0,08.10)}^{2}}=0,032J=32mJ\)
Lực từ tác dụng lên đoạn dây dẫn thẳng mang dòng điện đạt giá trị cực đại khi dây dẫn và véctơ cảm ứng từ của từ trường
Ta có, lực từ: \(F=BIl\sin \alpha \) với \(\alpha =(\overrightarrow{B},\overrightarrow{Il})\)
\(\Rightarrow {{F}_{max}}\)khi sina = 1 hay a = 900
\(\Rightarrow \) Lực từ tác dụng lên đoạn dây dẫn cực đại khi dây dẫn vuông góc với véctơ cảm ứng từ của từ trường.
Đặt điện áp u=U0cos\(\omega \)t vào hai đầu cuộn cảm thuần có độ tự cảm L. Tại thời điểm điện áp giữa hai đầu cuộn cảm có độ lớn cực đại thì cường độ dòng điện qua cuộn cảm bằng
Ta có mạch chỉ có cuộn cảm thuần \(\Rightarrow u\bot i\)
Khi điện áp giữa hai đầu cuộn cảm cực đại \(\Rightarrow \) Cường độ dòng điện qua cuộn cảm khi đó bằng 0A.
Đặt điện áp xoay chiều u = U0cos\(\omega \)t vào hai đầu đoạn mạch chỉ có điện trở thuần. Gọi U là điện áp hiệu dụng giữa hai đầu mạch; i, I0 và I lần lượt là giá trị tức thời, giá trị cực đại và giá trị hiệu dụng của cường độ dòng điện trong đoạn mạch. Hệ thức nào sau đây sai?
Mạch chỉ có điện trở thuần \(\Rightarrow u,i\) cùng pha
\(\Rightarrow \frac{u}{{{U}_{0}}}-\frac{i}{{{I}_{0}}}=\frac{u}{U}-\frac{i}{I}=0\text{ }\!\!~\!\!\text{ }\) và \(\text{ }\!\!~\!\!\text{ }\frac{U}{{{U}_{0}}}+\frac{I}{{{I}_{0}}}=\sqrt{2}\Rightarrow \text{A }\!\!~\!\!\text{ sai }\!\!~\!\!\text{ }\)
Hiện tượng đoản mạch là hiện tượng cường độ dòng điện trong mạch đạt giá trị
Hiện tượng đoản mạch là hiện tượng cường độ dòng điện trong mạch đạt giá trị cực đại do điện trở mạch ngoài bằng không.
Một vật dao động điều hòa có phương trình \(x=A\cos (\omega t+\varphi ).\) Gọi v và a lần lượt là vận tốc và gia tốc của vật. Hệ thức đúng là
Ta có hệ thức độc lập:
\(\left\{ \begin{array}{*{35}{l}} {{A}^{2}}={{x}^{2}}+\frac{{{v}^{2}}}{{{\omega }^{2}}} \\ {{A}^{2}}=\frac{{{v}^{2}}}{{{\omega }^{2}}}+\frac{{{a}^{2}}}{{{\omega }^{4}}} \\ \end{array} \right.\)
Suy ra: A, B, D – sai; C – đúng
Đặt điện áp \(u=100\cos \left( \omega t+\frac{\pi }{6} \right)V\) vào hai đầu đoạn mạch có điện trở thuần, cuộn cảm thuần và tụ điện mắc nối tiếp thì dòng điện qua mạch là \(i=2\cos \left( \omega t+\frac{\pi }{3} \right)A.\)Công suất tiêu thụ của đoạn mạch là
Công suất tiêu thụ của mạch:
\(P=UIcos\varphi =\frac{100}{\sqrt{2}}\cdot \frac{2}{\sqrt{2}}\cdot \cos \left( \frac{\pi }{6}-\frac{\pi }{3} \right)=50\sqrt{3}\text{W}\)
Một vật dao động điều hòa trên đoạn thẳng dài 10cm. Khi pha dao động bằng \(\frac{\pi }{3}\) thì vật có vận tốc \(v=-5\pi \sqrt{3}\text{cm/s}\text{.}\) Khi qua vị trí cân bằng vật có tốc độ là
Ta có:
+ Biên độ dao động: \(A=\frac{L}{2}=\frac{10}{2}=5\text{cm}\)
+ Khi \(\omega t+\varphi =\frac{\pi }{3}\) thì: \(v=-A\omega \sin (\omega t+\varphi )\Leftrightarrow -5\pi \sqrt{3}=-A\omega \sin \frac{\pi }{3}\Rightarrow A\omega =10\pi \)
Tại vị trí cân bằng, tốc độ của vật là \({{v}_{\max }}=A\omega =10\pi (c\text{m/s)}\)
Điện áp hai đầu bóng đèn có biểu thức \(u=100\sqrt{2}\cos 100\pi t(V).\) Đèn chỉ sáng khi \(\left| u \right|\ge 100\text{V}.\) Tỉ lệ thời gian đèn sáng – tối trong một chu kỳ là
+ Hiệu điện thế cực đại: \({{U}_{0}}=100\sqrt{2}(V)\)
+ Tần số góc: \(\omega =100\pi \) (rad/s)
+ Vẽ trên vòng tròn lượng giác, ta được:
.png)
Biết đèn chỉ sáng lên khi \(\left| u \right|\ge {{U}_{1}}=100\text{V}\)
Ta có: \(\cos \Delta \varphi =\frac{{{U}_{1}}}{{{U}_{0}}}=\frac{100}{100\sqrt{2}}=\frac{1}{\sqrt{2}}\Rightarrow \Delta \varphi =\frac{\pi }{4}\)
Thời gian đèn sáng trong 1 chu kì: \(\Delta t=\frac{4\Delta \varphi }{\omega }=\frac{4\frac{\pi }{4}}{100\pi }=\frac{1}{100}s\)
Thời gian đèn tắt trong 1 chu kì: \(\Delta {t}'=T-\Delta t=\frac{1}{50}-\frac{1}{100}=\frac{1}{100}s\)
\(\Rightarrow \) Tỉ lệ thời gian đèn sáng – tắt trong 1 chu kì là 1.
Tại một nổi trên mặt đất, một con lắc đơn dao động điều hòa. Trong khoảng thời gian \(\Delta t,\) con lắc thực hiện được 60 dao động toàn phần, thay đổi chiều dài con lắc một đoạn 44cm thì cũng trong khoảng thời gian \(\Delta t\) ấy, nó thực hiện 50 dao động toàn phần. Chiều dài ban đầu của con lắc là
+ Ban đầu: \(T=2\pi \sqrt{\frac{l}{g}}=\frac{\Delta t}{60}\)
+ Khi thay đổi chiều dài \({l}'=l+0,44:{T}'=2\pi \sqrt{\frac{{{l}'}}{g}}=\frac{\Delta t}{50}\)
\(\Rightarrow \frac{T}{{{T}'}}=\sqrt{\frac{l}{{{l}'}}}=\sqrt{\frac{l}{l+0,44}}=\frac{50}{60}\Rightarrow l=1m=100\text{cm}\)
Một máy biến thế có số vòng dây của cuộn sơ cấp là 800 vòng, của cuộn thứ cấp là 40 vòng. Hiệu điện thế và cường độ hiệu dụng ở mạch thứ cấp là 40V và 6A. Hiệu điện thế và cường độ hiệu dụng ở mạch
Ta có: \(\left\{ \begin{array}{*{35}{l}} {{N}_{1}}=800 \\ {{N}_{2}}=40 \\ {{U}_{2}}=40\text{V} \\ {{I}_{2}}=6\text{A} \\ \end{array} \right.\)
Lại có: \(\frac{{{U}_{1}}}{{{U}_{2}}}=\frac{{{N}_{1}}}{{{N}_{2}}}=\frac{{{I}_{2}}}{{{I}_{1}}}\Rightarrow \left\{ \begin{array}{*{35}{l}} {{U}_{1}}=800\text{V} \\ {{I}_{1}}=0,3\text{A} \\ \end{array} \right.\)
Sóng dọc trên một sợi dây dài lí tưởng với tần số 50Hz, vận tốc sóng là 200cm/s, biên độ sóng là 4cm. Tìm khoảng cách lớn nhất giữa 2 điểm A, B. Biết A, B nằm trên sợi dây, khi chưa có sóng lần lượt cách nguồn một khoảng là 20cm và 42cm.
+ Bước sóng: \(\lambda =\frac{v}{f}=\frac{200}{50}=4cm\)
+ Độ lệch pha giữa 2 điểm AB: \(\Delta \varphi =\frac{2\pi \Delta d}{\lambda }=\frac{2\pi (42-20)}{4}=11\pi \)
\(\Rightarrow \) Hai điểm do động ngược pha nhau
\(\Rightarrow \) Khoảng cách lớn nhất của 2 điểm A, B: \({{d}_{\max }}=\Delta {{u}_{AB}}+\Delta d=2\text{A}+\Delta d=2.4+(42-20)=30\text{cm}\)
Một con lắc đơn có chiều dài 1 = 1m dao động điều hòa với chu kỳ T tại nơi có gia tốc trọng trường là g = 10 = π2 (m/s2). Khi dao động qua vị trí cân bằng, dây treo bị vướng định tại vị trí \(\frac{l}{2}\) và con lắc tiếp tục dao động. Xác định chu kỳ của con lắc đơn khi đó.
Chu kì dao động của con lắc đơn khi đó:
\(T=\frac{1}{2}\left( {{T}_{1}}+{{T}_{2}} \right)\Rightarrow T=\frac{\pi }{\sqrt{g}}\left( {{\sqrt{l}}_{1}}+\sqrt{{{l}_{2}}} \right)=\frac{\pi }{\sqrt{g}}\left( \sqrt{1}+\sqrt{\frac{1}{2}} \right)=\frac{2+\sqrt{2}}{2}s\)
Dòng điện xoay chiều qua một đoạn mạch có biểu thức cường độ là \(i={{I}_{0}}\cos (\omega t+\pi )(A).\) Tính từ lúc t = 0, điện ượng chuyển qua mạch trong \(\frac{\text{T}}{4}\) đầu tiên là
Ta có, điện lượng chạy qua tiết diện dây:
\(\Delta q=\int\limits_{{{t}_{1}}}^{{{t}_{2}}}{i\text{d}t}=\int\limits_{0}^{\frac{T}{4}}{{{I}_{0}}\cos (\omega t+\pi ).dt}=\frac{{{I}_{0}}}{\omega }\sin (\omega t+\pi )\left| \underset{0}{\overset{\frac{T}{4}}{\mathop{{}}}}\, \right.=\frac{{{I}_{0}}}{\omega }(1-0)=\frac{{{I}_{0}}}{\omega }\)
Hai đầu cuộn thuần cảm \(L=\frac{2}{\pi }H\) có hiệu điện thế xoay chiều \(u=100\sqrt{2}\cos \left( 100\pi t-\frac{\pi }{2} \right)V.\) Pha ban đầu của cường độ dòng điện là
Ta có mạch chỉ có cuộn dây thuần cảm, u nhanh pha hơn một góc \(\frac{\pi }{2}\)
\(\Rightarrow {{\varphi }_{i}}={{\varphi }_{u}}-\frac{\pi }{2}=-\frac{\pi }{2}-\frac{\pi }{2}=-\pi (rad)\)
Mạch RLC nối tiếp có L thay đổi được. Điện áp 2 đầu mạch là \({{U}_{AB}}\) ổn định và tần số f = 50Hz. Điều chỉnh L sao cho cường độ hiệu dụng của mạch là cực đại. Biết \(C=\frac{{{10}^{-3}}}{15\pi }F.\) Độ tự cảm L có giá trị
L thay đổi có \({{I}_{\max }}\Rightarrow \) Mạch xảy ra hiện tượng cộng hưởng
Khi đó: \({{Z}_{L}}={{Z}_{C}}\Leftrightarrow \omega L=\frac{1}{\omega C}\Rightarrow L=\frac{1}{{{\omega }^{2}}C}=\frac{1}{{{(100\pi )}^{2}}\frac{{{10}^{-3}}}{15\pi }}=\frac{3}{2\pi }H\)
Một hộp kín X chỉ chứa 1 trong 3 phần tử là điện trở thuần R hoặc tụ điện có điện dung C hoặc cuộn cảm thuần có độ tự cảm L. Đặt vào 2 đầu hộp X một điện áp xoay chiều có phương trình u = U0cos(2πf)(V) , với f = 50Hz thì thấy điện áp và dòng điện trong mạch ở thời điểm t1 có giá trị lần lượt là i1 = 1A; u = 100\(\sqrt{3}\)V , ở thời điểm t2 thì i2 =\(\sqrt{3}A;\) u2 =100V . Biết nếu tần số điện áp là 100Hz thì cường độ dòng điện hiệu dụng trong mạch là \(\frac{1}{\sqrt{2}}\)A. Hộp X chứa
Ta thấy \(\frac{{{u}_{1}}}{{{i}_{1}}}\ne \frac{{{u}_{2}}}{{{i}_{2}}}\Rightarrow \) Mạch kín không thể là R mà là cuộn dây hoặc tụ điện.
Khi đó, ta có: (\({{\left( \frac{{{i}_{1}}}{{{I}_{0}}} \right)}^{2}}+{{\left( \frac{{{u}_{1}}}{{{U}_{0}}} \right)}^{2}}={{\left( \frac{{{i}_{2}}}{{{I}_{0}}} \right)}^{2}}+{{\left( \frac{{{u}_{2}}}{{{U}_{0}}} \right)}^{2}}=1\) (1)
\(\frac{i_{2}^{2}-i_{1}^{2}}{u_{1}^{2}-u_{2}^{2}}=\frac{I_{0}^{2}}{U_{0}^{2}}\Rightarrow Z=\frac{{{U}_{0}}}{{{I}_{0}}}=\sqrt{\frac{u_{1}^{2}-u_{2}^{2}}{i_{2}^{2}-i_{1}^{2}}}=100\Omega \)
Thay vào (1) ta suy ra: \({{I}_{0}}=2\text{A}\Rightarrow I=\sqrt{2}A\)
Khi tần số f = 100Hz thì cường độ dòng điện giảm \(I=\frac{1}{\sqrt{2}}A\)
\(\Rightarrow \) Hộp kín là cuộn cảm thuần có độ tự cảm: \(L=\frac{Z}{{{\omega }_{1}}}=\frac{100}{50.2\pi }=\frac{1}{\pi }H\)
Đặt điện áp u = 200cos100πt (V) vào hai đầu đoạn mạch gồm một biến trở R mắc nối tiếp với một cuộn cảm thuần có độ tự cảm \(\frac{1}{\pi }\)H. Điều chỉnh biến trở để công suất tỏa nhiệt trên biến trở đạt cực đại, khi đó cường độ dòng điện hiệu dụng trong đoạn mạch bằng
Mạch có R thay đổi khi R = Z, thì công suất tỏa nhiệt trên biến trở cực đại.
Khi đó: \(I=\frac{U}{Z}=\frac{U}{\sqrt{2}{{Z}_{L}}}=\frac{100\sqrt{2}}{\sqrt{2}.100}=1\text{A}\)
Một máy bay bay ở độ cao h1=100m, gây ra ở mặt đất ngay phía dưới tiếng ồn có mức cường độ âm L1 = 120(dB). Coi môi trường không hấp thụ âm. Muốn giảm tiếng ồn tới mức chịu được L2 =100dB thì máy bay phải bay ở độ cao
+ Khi máy bay ở độ cao h1 = 100m: L1 =120dB
+ Khi máy bay ở độ cao h: L2 = 100dB
\({{L}_{2}}-{{L}_{1}}=10\log \frac{{{I}_{2}}}{{{I}_{1}}}=10\log {{\left( \frac{{{h}_{1}}}{{{h}_{2}}} \right)}^{2}}\Leftrightarrow 100-120=20\log \frac{{{h}_{1}}}{{{h}_{2}}}\Rightarrow {{h}_{2}}=\frac{{{h}_{1}}}{{{10}^{-1}}}=1000\text{m}\)
Sóng dừng trên sợi dây có chiều dài l, bước sóng \(\lambda \)= 16cm . Xét điểm O trùng với một nút sóng, các điểm M, N, P, Q nằm về một phía của điểm O cách O những đoạn tương ứng là: 59cm, 87cm, 106cm, 143cm. Pha dao động của các điểm trên có tính chất gì?
Ta có:
\(\left\{ \begin{align} & OM=59\text{cm}=3\lambda +\frac{11\lambda }{16} \\ & ON=87\text{cm}=5\lambda +\frac{7\lambda }{16} \\ & OP=106\text{cm}=6\lambda +\frac{5\lambda }{8} \\ & OQ=143\text{cm}=8\lambda +\frac{15\lambda }{16} \\ \end{align} \right.\)
Ta có mọi điểm nằm 2 bên của 1 nút của sóng dừng đều dao động ngược pha.
\(\Rightarrow \) M và N cùng pha với nhau (cùng nằm bó chẵn), P và Q cùng pha với nhau (cùng nằm bó lẻ).
Một con lắc đơn có chiều dài 45cm với vật nhỏ có khối lượng 102g, mang điện tích \(2\mu C.\) Khi con lắc đang đứng cân bằng thì đặt một điện trường đều có véctơ cường độ điện trường hướng theo phương ngang và có độ lớn 3,5.104 V/m trong quãng thời gian 0,336s rồi tắt điện trường. Lấy g = 9,81(m/s2), π = 3,14. Tốc độ cực đại của vật nhỏ trong quá trình dao động sau đó xấp xỉ là
+ Chu kì dao động của con lắc: \(T=2\pi \sqrt{\frac{l}{g}}=1,345\text{s}\)
+ Khi đặt vào điện trường, con lắc lệch khỏi VTCB ban đầu 1 góc α với :
\(\tan \alpha =\frac{F}{P}=\frac{qE}{mg}=\frac{{{2.10}^{-6}}.3,{{5.10}^{4}}}{0,102.9,81}\approx 0,07\Rightarrow \alpha \approx 0,07\text{rad}\)
Khi đó, con lắc có VTCB mới lệch 0,07rad theo chiều điện trường.
Lúc t = 0 con lắc ở vị trí biên âm
Khi t = 0,336s = \(\frac{T}{4}\) con lắc ở CTCB mới và vận tốc khi này \(v=\alpha \omega \)
Khi tắt điện trường thì VTCB trở lại ban đầu \(\Rightarrow {{\alpha }_{0}}=\sqrt{{{\alpha }^{2}}+\frac{{{v}^{2}}}{{{\omega }^{2}}}}=\alpha \sqrt{2}=0,07\sqrt{2}(\text{rad})\)
\(\Rightarrow {{v}_{\max }}=\sqrt{2gl\left( 1-\cos {{\alpha }_{0}} \right)}=20,78\text{cm/s}\)
Đặt một điện áp xoay chiều u = U0cos(cos\(\omega t\)) vào hai đầu đoạn mạch AB gồm điện trở R = 50Ω, cuộn dây có điện trở r = 5Ω và tụ điện có điện dung thay đổi được, mắc nối tiếp theo thứ tự trên. M là điểm nối giữa R và cuộn dây. N là điểm nối giữa cuộn dây và tụ điện. Khi C = C1 thì điện áp hiệu dụng hai đầu đoạn MB đạt giá trị cực tiểu bằng U1. Khi C = \({{C}_{2}}=\frac{{{C}_{1}}}{2}\) thì điện áp hiệu dụng giữa hai đầu đoạn mạch NB đạt giá trị cực đại bằng \({{\text{U}}_{2}}.\) Tỉ số \(\frac{{{\text{U}}_{\text{2}}}}{{{\text{U}}_{\text{1}}}}\) bằng
+ \({{U}_{M{{B}_{\min }}}}\)khi \({{Z}_{{{C}_{1}}}}={{Z}_{L}}\) khi đó: \({{U}_{M{{B}_{\min }}}}={{U}_{r}}=\frac{U}{R+r}r={{U}_{1}}\Rightarrow {{U}_{1}}=\frac{U}{11}\)
+ Khi \(C={{C}_{2}}=\frac{{{C}_{1}}}{2}\Rightarrow {{Z}_{{{C}_{2}}}}=2{{\text{Z}}_{{{C}_{1}}}}\)thì \({{U}_{N{{B}_{\text{max }\!\!~\!\!\text{ }}}}}\left( {{U}_{{{C}_{\text{max }\!\!~\!\!\text{ }}}}} \right)\) khi đó
\({{Z}_{{{C}_{2}}}}=2{{Z}_{{{C}_{1}}}}=\frac{{{(R+r)}^{2}}+Z_{L}^{2}}{{{Z}_{L}}}\Leftrightarrow 2{{Z}_{L}}=\frac{{{(R+r)}^{2}}+Z_{L}^{2}}{{{Z}_{L}}}\Rightarrow R+r={{Z}_{L}}\Rightarrow {{U}_{R+r}}={{U}_{L}}\)
\({{U}_{2}}=\frac{U\sqrt{{{(R+r)}^{2}}+Z_{L}^{2}}}{R+r}=U\sqrt{2}\Rightarrow \frac{{{U}_{2}}}{{{U}_{1}}}=\frac{U\sqrt{2}}{\frac{U}{11}}=11\sqrt{2}A\)
Hai đầu đoạn mạch RLC, cuộn dây thuần cảm, duy trì điện áp \({{u}_{AB}}={{U}_{0}}\cos \omega t(V).\) Thay đổi R, khi điện trở có giá trị R = 24Ω thì công suất tiêu thụ của mạch đạt cực đại 300W. Hỏi khi điện trở bằng 15Ω thì mạch điện tiêu thụ công suất xấp xỉ bằng bao nhiêu?
+ Khi R = 24Ω thì công suất tiêu thụ của mạch đạt cực đại
Khi đó, ta có: \(\left\{ \begin{array}{*{35}{l}} \left| {{Z}_{L}}-{{Z}_{C}} \right|=R=24\Omega \\ P=\frac{{{U}^{2}}}{2R}=300W\Rightarrow U=120V \\ \end{array} \right.\)
+ Khi R = 15Ω, công suất tiêu thụ của mạch khi này;
\(P=\frac{{{U}^{2}}}{{{Z}^{2}}}R=\frac{{{U}^{2}}}{\left( {{R}^{2}}+{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}} \right)}R=\frac{{{120}^{2}}}{{{15}^{2}}+{{24}^{2}}}.15=269,66W\)
Một con lắc lò xo dao động điều hòa theo phương thẳng đứng. Tại thời điểm lò xo dãn a thì tốc độ của vật là \(\sqrt{8}\)b. Tại thời điểm lò xo dãn 2a thì tốc độ của vật là \(\sqrt{6}\)b . Tại thời điểm lò xo dãn 3a thì tốc độ của vật là \(\sqrt{2}\)b. Chọn mốc thế năng tại vị trí cân bằng. Tại vị trí lò xo bị nén 2a thì tỷ số giữa động năng và thế năng của vật là
Ta có: \(\left\{ \begin{align} & {{\left( a-\Delta {{l}_{0}} \right)}^{2}}+{{\left( \frac{\sqrt{8}b}{\varpi } \right)}^{2}}={{A}^{2}}\text{ (1}) \\ & {{\left( 2\text{a}-\Delta {{l}_{0}} \right)}^{2}}+{{\left( \frac{\sqrt{6}b}{\omega } \right)}^{2}}={{A}^{2}}\text{ }(2) \\ & {{\left( 3a-\Delta {{l}_{0}} \right)}^{2}}+{{\left( \frac{\sqrt{2b}}{\omega } \right)}^{2}}={{A}^{2}}\text{ }(3) \\ \end{align} \right.\)
Để đơn giản, ta chuẩn hóa \(\Delta {{l}_{0}}=1\) từ (1), (2) ta được:
\(\left\{ \begin{array}{*{35}{l}} 2\frac{{{b}^{2}}}{{{\omega }^{2}}}=3{{a}^{2}}-2a \\ {{A}^{2}}=13{{a}^{2}}-10a+1 \\ \end{array} \right.\)
Thế vào (3) ta suy ra \(\left\{ \begin{array}{*{35}{l}} a=2 \\ A=\sqrt{33} \\ \end{array} \right.\)
Tại vị trí lò xo nén 2a, li độ khi đó: \(x=2a+\Delta {{l}_{0}}\)
Thế năng tại đó: \({{\text{W}}_{t}}=\frac{1}{2}k{{\text{x}}^{2}}=\frac{1}{2}k{{(2.2+1)}^{2}}=\frac{25k}{2}\)
Cơ năng: \(\text{W}=\frac{1}{2}k{{\text{A}}^{2}}=\frac{33k}{2}\)
Động năng khi đó: \({{\text{W}}_{d}}=\text{W}-{{\text{W}}_{t}}=\frac{33}{2}k-\frac{25}{2}k=\frac{8k}{2}\)
\(\Rightarrow \) Tỉ số giữa động năng và thế năng là: \(\frac{{{\text{W}}_{d}}}{{{W}_{t}}}=\frac{8}{25}\)
Trên mặt thoáng chất lỏng, tại A và B cách nhau 20cm, người ta bố trí hai nguồn đồng bộ có tần số 20Hz. Tốc độ truyền sóng trên mặt thoáng chất lỏng v = 50cm/s. Hình vuông ABCD nằm trên mặt thoáng chất lỏng. I là trung điểm CD. Gọi điểm M nằm trên CD là điểm gần I nhất dao động với biên độ cực đại. Tính khoảng cách từ M đến I?
.png)
Ta có:
+ Bước sóng: \(\lambda =\frac{v}{f}=\frac{50}{20}=2,5\text{cm}\)
Đặt MI = x
Ta có: \(0
Để M dao động cực đại và gần I nhất
\(\Rightarrow \) M thuộc cực đại bậc 1 tính từ trung trực của AB
\(\Rightarrow \) MB – MA = \(\lambda \)
\(\Leftrightarrow \sqrt{{{(OB+x)}^{2}}+I{{O}^{2}}}-\sqrt{{{(OA-x)}^{2}}+I{{\text{O}}^{2}}}=\lambda \)
\(\Leftrightarrow \sqrt{{{(10+x)}^{2}}+{{20}^{2}}}-\sqrt{{{(10-x)}^{2}}+{{20}^{2}}}=2,5\Rightarrow x=2,813\text{cm}\)

