Đề thi thử THPT QG năm 2021 môn Vật Lý - Trường THPT Lương Hữu Phước
Đề thi thử THPT QG năm 2021 môn Vật Lý
-
Hocon247
-
40 câu hỏi
-
90 phút
-
45 lượt thi
-
Dễ
Tham gia [ Hs Hocon247.com ] - Cộng Đồng Luyện Thi Trực Tuyến để được học tập những kiến thức bổ ích từ HocOn247.com
Chọn câu trả lời đúng khi nói về dao động điều hòa:
Tốc độ cực đại của chất điểm dao động điều hòa là vmax = ωA
Số prôtôn và số nơtron trong hạt nhân nguyên từ \(_{30}^{67}Zn\) lần lượt là:
Ta có:
\(\left\{ \begin{array}{l}
Z = 30\\
A = 67
\end{array} \right. \Rightarrow N = A - Z = 37\)
Đặt vào hai đầu điện trở R = 100 Ω thì dòng điện trong mạch có biểu thức \(i = 2\sqrt 2 \cos 100\pi t\)(A). Điện áp hiệu dụng đặt vào hai đầu R là:
Ta có: U = I.R = 2.100 = 200 (V)
Một máy biến áp lí tưởng có số vòng dây ở cuộn sơ cấp là N1, ở cuộn thứ cấp là N2. Khi đặt vào hai đầu cuộn sơ cấp điện áp U1 thì điện áp ở cuộn thứ cấp là:
Công thức máy biến áp:
\(\frac{{{U_2}}}{{{U_1}}} = \frac{{{N_2}}}{{{N_1}}} \Rightarrow {U_2} = {U_1}\frac{{{N_2}}}{{{N_1}}}\)
Đặt điện áp xoay chiều u = U0cosωt vào hai đầu một đoạn mạch gồm tụ điện và cuộn cảm thuần có độ tự cảm L mắc nối tiếp. Tổng trở của đoạn mạch là:
Tổng trở:
\(\begin{array}{l}
Z = \sqrt {{R^2} - {{\left( {{Z_L} - {Z_C}} \right)}^2}} \\
Z = \left| {{Z_L} - {Z_C}} \right| = \left| {\omega L - \frac{1}{{\omega C}}} \right|
\end{array}\)
Cho đoạn mạch điện xoay chiều không phân nhánh gồm cuộn dây thuần cảm có L = 2/π (H), tụ điện C = 10-4/π (F) và một điện trở thuần R. Điện áp đặt vào hai đầu đoạn mạch và cường độ dòng điện qua đoạn mạch có biểu thức u = U0cos100πt (V) và \(i = {I_0}\cos \left( {100\pi t - \frac{\pi }{4}} \right)\). Điện trở R có giá trị là:
Ta có:
\(\begin{array}{l}
{Z_L} = 200\Omega ;{Z_C} = 100\Omega \\
\varphi = {\varphi _u} - {\varphi _i} = \frac{\pi }{4} \Rightarrow \tan \varphi = \frac{{{Z_L} - {Z_C}}}{R}\\
\Leftrightarrow 1 = \frac{{200 - 100}}{R} \Rightarrow R = 100\Omega
\end{array}\)
1 chất điểm dddh với phương trình gia tốc a = 160cos\(\left( {2\pi t + \frac{\pi }{3}} \right)\)cm/s2. Lấy π2 = 10. Chọn câu trả lời đúng:
Gia tốc cực đại: amax = ω2Α <=> 160 = (2π)2.Α => Α = 4 (cm)
Khi nói về sóng cơ học, phát biểu nào sau đây là sai?
Sóng cơ không truyền được trong chân không => B sai
Một sóng cơ khi truyền theo trục Ox có phương trình là: u = 5cos(6πt - πx) (cm), với t đo bằng s, x đo bằng m. Tốc độ truyền sóng này là:
Ta có:
\(\frac{{2\pi x}}{\lambda } = \pi x \Rightarrow \lambda = 2\left( m \right) \Rightarrow v = \lambda f = 6\left( {m/s} \right)\)
Đại lượng không phải là đặc trưng vật lý của âm?
Độ cao của âm là đặc trưng sinh lý của âm.
Câu nào đúng. Sóng điện từ
+ Sóng điện từ là sóng ngang => A sai
+ Sóng điện tử là quá trình lan truyền điện từ trường trong không gian => B đúng
+ Sóng điện từ có E và B dao động theo phương vuông góc nhau => C sai
+ Sóng điện từ truyền được trong chân không => D sai
=> Chọn B.
Sóng vô tuyến do đài VOV3 phát ra có tần số 102,7 MHz, khi truyền trong không khí có bước sóng là bao nhiêu? Lấy tốc độ truyền sóng điện từ trong không khí là c = 3.108 m/s.
Ta có:
\(\lambda = \frac{c}{f} = \frac{{{{3.10}^8}}}{{{{102,7.10}^6}}} = 2,92\left( m \right)\)
Hiện tượng nhiễu xạ và giao thoa ánh sáng chứng tỏ ánh sáng
Hiện tượng nhiều xạ và giao thoa ánh sáng chứng tỏ ánh sáng có tính chất sóng => Chọn A.
Chiếu một chùm sáng đơn sắc hẹp tới mặt bên của một lăng kính thủy tinh đặt trong không khí. Khi đi qua lăng kính, chùm sáng này
Vì ánh sáng đơn sắc nên khi đi qua lăng kính nó không bị tán sắc mà chỉ bị lệch đường đi.
Trong thí nghiệm của Y-âng về giao thoa với ánh sáng đon sắc, khoảng cách giữa vân sáng và vân tối liền kề là 1 mm. Trên màn, tại điểm M cách vân trung tâm một khoảng 6mm có
Khoảng cách giữa vân sáng và vân tối liền kề là:
\(\begin{array}{l}
\frac{i}{2} = 1 \Rightarrow i = 2\left( {mm} \right)\\
\frac{x}{i} = \frac{6}{2} = 3 = k
\end{array}\)
vân sáng bậc 3
Theo thuyết của Anh-xtanh về lượng tử ánh sáng, phôtôn ứng với mỗi ánh sáng đơn sắc có năng lượng càng lớn nếu ánh sáng đơn sắc đó có
Năng lượng phô-tôn của mỗi ánh sáng đơn sắc:
\(\varepsilon = hf = \frac{{hc}}{\lambda }\)
Biết công thoát A của electron khỏi một kim loại là 4,14 eV. Giới hạn quang điện của kim loại đó gần nhất với giá trị nào sau đây:
Ta có:
\(A = \frac{{hc}}{{{\lambda _0}}} \Rightarrow {\lambda _0} = \frac{{hc}}{A} \approx {3.10^{ - 7}}\left( m \right) \approx 0,3\left( {\mu m} \right)\)
Khi nghiên cứu quang phổ của các chất, chất nào dưới đây khi bị nung nóng đến nhiệt độ cao thì không phát ra quang phổ liên tục?
Các chất rắn, lỏng và khí ở áp suất cao khi bị nung nó thì phát ra quang phổ liên tục.
Chọn câu sai về các tia bức xạ:
+ Tia hồng ngoại là những bức xạ có bước sóng λ > 0,76 µm đến vài mm
+ Tia hồng ngoại nằm ngoài vùng ánh sáng nhìn thấy nên mắt người không có cảm giác màu => D sai
Một dải sóng điện từ trong chân không có tần số \({4,0.10^{14}}\;Hz - {7,5.10^{14}}\;Hz\). Biết vận tốc ánh sáng trong chân không c = 3.108 m/s. Dải sóng trên thuộc vùng nào trong thang sóng điện từ?
dài sóng thuộc vùng ánh sáng nhìn thấy
Một CLLX gồm một lò xo nhẹ có độ cứng k, vật nặng có khối lượng m = 100g. Kích thích cho vật dao động điều hòa trên mặt phẳng nằm ngang với biểu thức của lực hồi phục là F = -5cos\(\left( {10\pi t + \frac{\pi }{2}} \right)\) (N) (t đo bằng giây). Lấy π2 = 10. Chọn câu trả lời đúng:
Tần số của con lắc lò xo: \(f = \frac{\omega }{{2\pi }} = \frac{{10\pi }}{{2\pi }} = 5Hz\) => A sai
+ Độ cứng của lò xo:
\({\omega ^2} = \frac{k}{m} \Rightarrow k = m{\omega ^2} = 0,1.{\left( {10\pi } \right)^2} = 100\left( {N/m} \right)\)=> B sai
+ Vì F sớm pha hơn x một góc π nên pha ban dầu của dao động là:
\(\varphi = {\varphi _F} - \pi = - \frac{\pi }{2}\) => C sai
+ Lực hồi phục cực đại:
\({F_{\max }} = m{\omega ^2}A \Leftrightarrow 5 = 0,1.{\left( {10\pi } \right)^2}.A\)
=> A = 0,05 (m) => D đúng
Đặt điện áp u = U0cos\(\left( {100\pi t - \frac{\pi }{{12}}} \right)\) (V) vào hai đầu đoạn mạch mắc nối tiếp gồm điện trở, cuộn cảm và tụ điện thì hiệu điện thế giữa hai bản tụ là uC = U0Ccos\(\left( {100\pi t - \frac{\pi }{3}} \right)\) V. Hệ số công suất của đoạn mạch bằng:
Vì dòng điện i sớm pha hơn uC góc \(\frac{\pi }{2} \Rightarrow {\varphi _1} = - \frac{\pi }{3} + \frac{\pi }{2} = \frac{\pi }{6}\)
+ Độ lệch pha giữa u và i:
\(\varphi = {\varphi _u} - {\varphi _i} = - \frac{\pi }{{12}} - \frac{\pi }{6} = - \frac{\pi }{4}\)
+ Hệ số công suất:
\(\cos \varphi = \frac{{\sqrt 2 }}{2}\)
Độ bền vững của hạt nhân phụ thuộc vào:
Độ bền vững của hạt nhân phụ thuộc vào năng lượng liên kết riêng
Ta có:
\(\Delta {E_{lkr}} = \frac{{{W_{lk}}}}{A} = \frac{{\Delta m.{c^2}}}{A}\)
=> phụ thuộc vào tỉ số giữa độ hụt khối và số khối
Cho đồ thị biểu diễn li độ của một vật dao động điều hòa theo thời gian t như hình bên. Biết A là biên độ, T là chu kì dao động. Tại thời điểm t = 3T/4 vật có vận tốc và gia tốc là:
.png)
Từ đồ thị ta thấy, lúc t=3T/4 => x = 0
+ Lại có:
\(\left\{ \begin{array}{l}
{A^2} = {x^2} + \frac{{{v^2}}}{{{\omega ^2}}}v = \pm \omega A\\
a = - {\omega ^2}xa = 0
\end{array} \right.\)
+ Theo đồ thị, lúc t = 3T/4 vật qua VTCB theo chiều âm nên v < 0
Một máy bay bay ở độ cao 100m, gây ra ở mặt đất ngay phía dưới tiếng ồn có mức cường độ âm L1 = 130 dB. Giả thiết máy bay là nguồn điểm. Nếu muốn giảm tiếng ồn xuống mức chịu đựng được là L2 = 100 dB thì máy bay phải bay ở độ cao bao nhiêu?
Ta có:
\(\begin{array}{l}
{L_1} - {L_2} = 10\lg \frac{{{I_1}}}{{{I_2}}} = 10\lg {\left( {\frac{{{R_2}}}{{{R_1}}}} \right)^2}\\
\Rightarrow \frac{{{R_2}}}{{{R_1}}} = 31,623\\
\Rightarrow {R_2} = 3162,3\left( m \right)
\end{array}\)
Trên một phương truyền sóng có hai điểm M và N cách nhau 80cm. Sóng truyền theo chiều từ M đến N với bước sóng là 1,6m. Coi biên độ của sóng không đổi trong quá trình truyền sóng. Biết phương trình sóng tại N là \(u = 8\cos \left[ {\frac{\pi }{4}\left( {t - 4} \right)} \right]\) (cm) thì phương trình sóng tại M là:
Vì sóng truyền từ M đến N nên sóng ở M sớm pha hơn ở N một góc:
\(\begin{array}{l}
\Delta \varphi = \frac{{2\pi MN}}{\lambda } = \pi \\
\Rightarrow {u_M} = 8\cos \left[ {\frac{\pi }{4}\left( {t - 4} \right) + \pi } \right] = 8\cos \left( {\frac{\pi }{4}t} \right)
\end{array}\)
Hiện nay đèn LED đang có những bước nhảy vọt trong ứng dụng thị trường dân dụng và công nghiệp một cách rộng rãi như bộ phận hiển thị trong các thiết bị điện tử, đèn quảng cáo, đèn giao thông, trang trí nội thất, ngoại thất... Nguyên lý hoạt động của đèn LED dựa vào hiện tượng:
Đèn ống thông dụng (đèn nê-ôn) thuộc loại quang - phát quang
+ Đom đóm thuộc loại hóa - phát quang
+ Màn hình vô tuyến thuộc loại catot phát quang
+ Đèn LED thuộc loại điện phát quang
Một người đi xe máy trên đoạn đường cứ 6 m lại có ổ gà, tần số dao động khung xe là 2 Hz. Để tránh rung lắc mạnh nhất người đó phải tránh tốc độ nào sau đây:
+ Khi rung lắc mạnh nhất => xảy ra cộng hưởng
friêng = fcb = 2Hz => Tcb = 0,5 s
+ Lại có:
\(v = \frac{s}{{{T_{cb}}}} = \frac{6}{{0,5}} = 12\left( {m/s} \right) = 43,2\left( {km/h} \right)\)
Một chất phóng xạ có hằng số phóng xạ λ. Ở thời điểm ban đầu có N0 hạt nhân. Số hạt nhân đã bị phân rã sau thời gian t là:
Số hạt còn lại sau thời gian t:
\(N = {N_0}{.2^{\frac{{ - t}}{T}}} = {N_0}.{e^{ - \lambda t}}\)
Số hạt bị phân rã sau thời gian t:
\(\Delta N = {N_0} - N = {N_0}\left( {1 - {2^{\frac{{ - t}}{T}}}} \right) = {N_0}\left( {1 - {e^{ - \lambda t}}} \right)\)
Cho phản ứng hạt nhân \(_2^4He + _7^{14}N \to _1^1H + _Z^AX\). Hạt nhân \(_Z^AX\) là:
Áp dụng bảo toàn số khối và bảo toàn điện tích, ta có:
\(\left\{ \begin{array}{l}
4 + 14 = 1 + A \Rightarrow A = 17\\
2 + 7 = 1 + Z \Rightarrow Z = 8
\end{array} \right. \Rightarrow X = _8^{17}O\)
Bắn hạt prôtôn với động năng Wp = 1,46MeV vào hạt nhân Li đứng yên, tạo ra hai hạt nhân giống nhau có cùng khối lượng là mX và cùng động năng. Cho mLi = 7,0142u, mp = l,0073u, mX = 4,0015u, 1u = 931,5MeV/c2. Hai hạt sau phản ứng có vectơ vận tốc hợp nhau một góc gần nhất với giá trị nào sau đây:
Bảo toàn động lượng, ta có:
\(\begin{array}{l}
{\overrightarrow p _p} = {\overrightarrow p _X} + {\overrightarrow p _X}\\
\Leftrightarrow p_p^2 = p_X^2 + p_X^2 + 2p_X^2\cos \alpha \\
\Leftrightarrow p_p^2 = 2p_X^2\left( {1 + \cos \alpha } \right)\\
\Leftrightarrow {m_p}{W_p} = 2{m_X}{W_X}\left( {1 + \cos \alpha } \right)\\
\Rightarrow \cos \alpha = \frac{{{m_p}{W_p}}}{{2{m_X}{W_X}}} - 1
\end{array}\)
Thay (1) vào (2), ta có: cosα = -0,98 => α = 168,62°
Trong thí nghiệm giao thoa Y-âng, thực hiện đồng thời với hai ánh sáng đơn sắc có λ1 = 0,4 μm và λ2 = 0,6 µm. M là một điểm thuộc vân sáng bậc 6 của λ1 và O là vân sáng trung tâm. Số vân sáng đếm được trên đoạn MO là:
Ta có: \(\frac{{{k_1}}}{{{k_2}}} = \frac{{{\lambda _2}}}{{{\lambda _1}}} = \frac{{0,6}}{{0,4}} = \frac{3}{2}\)
=> từ O trở ra, vị trí hai vân sáng trùng nhau đầu tiên ứng với bậc 3 của λ1 và bậc 2 của λ2.
+ Ta vẽ được hệ hai vân như hình.
+ Vì O thuộc bậc 0 và M thuộc bậc 6 của λ1 nên O và M được xác định như trên hình
+ Từ hình ta đếm được số vân sáng (vạch sáng) trên đoạn OM là 9 vân (có 4 vân có màu λ1; 2 vân có màu λ2 và 3 vân sáng trùng có màu λ12)
Một đám nguyên tử hiđrô đang ở trạng thái cơ bản. Khi chiếu bức xạ có tần số f1 vào đám nguyên tử này thì chúng phát ra tối đa 3 bức xạ. Khi chiếu bức xạ có tần số f2 vào đám nguyên tử này thì chúng phát ra tối đa 10 bức xạ. Biết năng lượng ứng với các trạng thái dừng của nguyên tử hiđrô được tính theo biểu thức En=-E0/n2 (E0 là hằng số dương, n = 1, 2, 3,...). Tỉ số f1/f2 là:
+ Khi kích thích đám nguyên tử thì số bực xạ tối đa có thể phát là \(\frac{{n\left( {n - 1} \right)}}{2}\)
+ Khi hấp thu f1 thì: \(\frac{{{n_1}\left( {{n_1} - 1} \right)}}{2} = 3 \Rightarrow {n_1} = 3\)
+ Khi hấp thụ f2 thì: \(\frac{{{n_2}\left( {{n_2} - 1} \right)}}{2} = 10 \Rightarrow {n_2} = 5\)
+ Theo tiên đề 2, ta có:
\(\frac{{h{f_1}}}{{h{f_2}}} = \frac{{{E_3} - {E_1}}}{{{E_5} - {E_1}}}\frac{{{f_1}}}{{{f_2}}} = \frac{{ - \frac{1}{{{3^2}}} - \left( { - \frac{1}{{{1^2}}}} \right)}}{{ - \frac{1}{{{5^2}}} - \left( { - \frac{1}{{{1^2}}}} \right)}} \Rightarrow \frac{{{f_1}}}{{{f_2}}} = \frac{{25}}{{27}}\)
Hiện tượng nào dưới đây nhằm khẳng định ánh sáng có tính chất sóng?
Hiện tượng giao thoa ánh sáng khẳng định ánh sáng có tính chất sóng.
Trên mặt nước có hai nguồn sóng giống nhau A, B dao dộng cùng pha với biên độ sóng không đổi bằng a, cách nhau một khoảng AB = 12cm. C và D là hai điểm khác trên mặt nước, cách đều hai nguồn và cách trung điểm O của AB một khoảng 8cm. Biết bước sóng λ = 1,6cm. Số điểm dao động ngược pha với 2 nguồn có trên CD là:
+ Điểm M ngược pha với nguồn A khi:
\(x = AM = \left( {2k + 1} \right)\frac{\lambda }{2}\)
+ Vì C và D đối xứng qua AB nên ta sẽ tìm số điểm ngược pha trên OC sau đó lấy đối xứng suy ra trên CD.
+ Từ hình vẽ, ta có:
\(\begin{array}{l}
AO \le AM \le AC\\
\Leftrightarrow 6 \le 0,8\left( {2k + 1} \right) \le 10\\
\Rightarrow 3,25 \le k \le 5,75 \Rightarrow k = 4,5
\end{array}\)
=>trên OC có 2 điểm
+ Do tính đối xứng nên trên CD có 4 điểm
Một con lắc đơn gồm dây treo có chiều dài 1 m và vật nhỏ có khối lượng 100g mang điện tích 2.10-5 C. Treo con lắc đơn này trong điện trường đều với vectơ cường độ điện trường hướng theo phương ngang và có độ lớn 5.104 V/m. Trong mặt phẳng thẳng đứng đi qua điểm treo và song song với vectơ cường độ điện trường, kéo vật nhỏ theo chiều của vectơ cường độ điện trường sao cho dây treo hợp với vectơ gia tốc trọng trường g một góc 54° rồi buông nhẹ cho con lắc dao động điều hòa. Lấy g = 10 m/s2. Trong quá trình dao động, lực căng dây cực đại gần nhất với giá trị nào sau đây?
.png)
+ Gia tốc trọng trường hiệu dụng:
\({g^/} = \sqrt {{g^2} + {{\left( {\frac{{qE}}{m}} \right)}^2}} = 10\sqrt 2 \left( {m/{s^2}} \right)\)
+ Khi dây treo cân bằng thì tạo với phương thẳng đứng góc β được xác định bởi:
\(\cos \beta = \frac{g}{{{g^/}}} = \frac{{10}}{{10\sqrt 2 }} = \frac{{\sqrt 2 }}{2} \Rightarrow \beta = 45^\circ \)
+ Biên độ góc của con lắc:
\({\alpha _0} = 54 - 45 = 9^\circ = \frac{{9\pi }}{{180}} = \frac{\pi }{{20}}\) (rad)
+ Lực căng dây cực đại của dây treo:
\({T_{\max }} = m{g^/}\left( {3 - 2\cos {\alpha _0}} \right) = 1,45\left( N \right)\)
Đặt điện áp xoay chiều u=U√2cos(ωt + φ) (V) (với U và ω không đổi) vào hai đầu đoạn mạch AB nối tiếp gồm điện trở thuần R, cuộn dây không thuần cảm (có điện trở r), tụ điện, theo thứ tự đó. Biết R = r. Gọi M là điểm nối giữa R và cuộn dây, N là điểm nối giữa cuộn dây và tụ điện. Đồ thị biểu diễn điện áp uAN và uMB như hình vẽ bên. Giá trị của U gần nhất với giá trị nào sau đây:
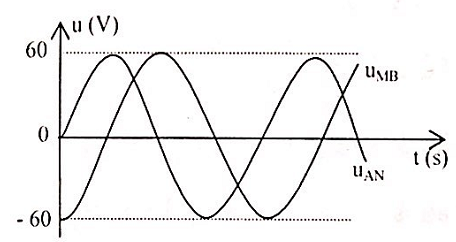
Ta có:
\(\begin{array}{l}
\left\{ \begin{array}{l}
{u_{AN}} = 60\cos \left( {\omega t - \frac{\pi }{2}} \right)\left( V \right)\\
{u_{MB}} = 60\cos \left( {\omega t + \pi } \right)\left( V \right)
\end{array} \right. \Rightarrow {u_{AN}} \bot {u_{MB}}\\
\Rightarrow \tan {\varphi _{AN}}.\tan {\varphi _{MB}} = - 1\\
\Leftrightarrow \frac{{{Z_L}}}{{2R}}.\frac{{{Z_L} - {Z_C}}}{R} = - 1\\
\Leftrightarrow {Z_L}\left( {{Z_C} - {Z_L}} \right) = 2{R^2}
\end{array}\) (1)
+ Lại có:
\({U_{AN}} = {U_{MB}} \Leftrightarrow 4{R^2} + Z_L^2 = {R^2} + {\left( {{Z_L} - {Z_C}} \right)^2} \Rightarrow 3{R^2} = Z_C^2 - 2{Z_L}{Z_C}\) (2)
+ Từ (1) và (2), ta có:
\( \Rightarrow \left\{ \begin{array}{l}
{Z_C} = 3{Z_L}\\
{Z_C} = 0,5{Z_L}
\end{array} \right.{Z_C} = 3{Z_L}R = {Z_L} \Rightarrow {Z_C} = 3R\)
+ Mặt khác, ta có:
\(\begin{array}{l}
{U_{AN}} = 60 = \frac{{U\sqrt {4{R^2} + Z_L^2} }}{{\sqrt {4{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }}\\
60 = \frac{{{U_0}\sqrt {4{R^2} + {R^2}} }}{{\sqrt {4{R^2} + 4{R^2}} }}\\
\Rightarrow {U_0} = 24\sqrt {10} \Rightarrow U \approx 54\left( V \right)
\end{array}\)
Ba con lắc lò xo có cùng độ cứng k, dao động điêu hòa cùng phương, cùng tần số. Tại cùng một thời điểm t nào đó li độ của các vật luôn thỏa mãn hệ thức x3 = x1 + x2. Biết cơ năng của x1, x2 và x3 lần lượt là W, 2W và 3W. Gốc tọa độ tại vị trí cân bằng. Tại thời điếm t, tỉ số |x2/x1|=9/8 thì tỉ số tốc độ |v2/v1| bằng:
Nhận thấy:
\(\begin{array}{l}
{W_3} = {W_1} + {W_2}\\
\Leftrightarrow \frac{1}{2}kA_3^2 = \frac{1}{2}kA_1^2 + \frac{1}{2}kA_2^2 \Leftrightarrow A_3^2 = A_1^2 + A_2^2\\
\Rightarrow {x_1} \bot {x_2} \Rightarrow \frac{{x_1^1}}{{A_1^2}} + \frac{{x_2^2}}{{A_2^2}} = 1 \Leftrightarrow \frac{{2{x_1}{v_1}}}{{A_1^2}} + \frac{{2{x_2}{v_2}}}{{A_2^2}} = 0\\
\Rightarrow \frac{{\left| {{v_1}} \right|}}{{A_1^2}} = \frac{{\left| {{v_2}} \right|}}{{A_2^2}}\left| {\frac{{{x_2}}}{{{x_1}}}} \right|\\
\Rightarrow \frac{{\left| {{v_1}} \right|}}{{A_1^2}} = \frac{{\left| {{v_2}} \right|}}{{A_2^2}}\frac{9}{8}\\
\Rightarrow \left| {\frac{{{v_2}}}{{{v_1}}}} \right| = \frac{8}{9}\frac{{A_2^2}}{{A_1^2}} = \frac{8}{9}\frac{{\frac{1}{2}kA_2^2}}{{\frac{1}{2}kA_1^2}} = \frac{8}{9}\frac{{{W_2}}}{{{W_1}}} = \frac{8}{9}.2 = \frac{{16}}{9}
\end{array}\)
Điện năng được truyền từ nơi phát đến một xưởng sản xuất bằng đường dây một pha với hiệu suất 90%. Ban đầu xưởng có 90 máy hoạt động, sau đó tăng thêm một số máy nên hiệu suất truyền tải điện giảm 10%. Biết điện áp nơi phát không đổi. Tìm số máy tăng thêm.
Ta có:
\(\begin{array}{l}
\left\{ \begin{array}{l}
h = 1 - H = \frac{{P.R}}{{{{\left( {U\cos \varphi } \right)}^2}}}\\
H = \frac{{{P_{tt}}}}{P} \Rightarrow P = \frac{{{P_{tt}}}}{H}
\end{array} \right.\\
\Rightarrow h = 1 - H = \frac{{{P_{tt}}.R}}{{H{{\left( {U\cos \varphi } \right)}^2}}}\\
\Rightarrow \left( {1 - H} \right)H = \frac{{{P_{tt}}.R}}{{{{\left( {U\cos \varphi } \right)}^2}}}\\
\frac{{\left( {1 - {H_1}} \right){H_1}}}{{\left( {1 - {H_2}} \right){H_2}}} = \frac{{{P_{tt1}}}}{{{P_{tt2}}}}\\
\Leftrightarrow \frac{{\left( {1 - 0,9} \right)0,9}}{{\left( {1 - 0,8} \right)0,8}} = \frac{{90}}{{90 + x}} \Rightarrow x = 70
\end{array}\)
Một mạch dao động LC có điện trở thuần bằng không gồm cuộn cảm thuần có độ tự cảm L và tụ điện có điện dung C. Trong mạch có dao động điện từ tự do. Tại thời điểm t1 tỉ số dòng điện tức thời và điện tích tức thời trên hai bản tụ \(\frac{{{i_1}}}{{{q_1}}} = \frac{1}{{\sqrt {3LC} }}\). Sau thời gian Δt tỉ số đó là \(\frac{{{i_2}}}{{{q_2}}} = \sqrt {\frac{3}{{LC}}} \). Giá trị nhỏ nhất của Δt là:
+ Vì mạch LC nên i vuông pha với q nên:
\(\frac{{{i^2}}}{{I_0^2}} + \frac{{{q^2}}}{{Q_0^2}} = 1\frac{{{i^2}}}{{{\omega ^2}}} + {q^2} = Q_0^2\)
+ Tại thời điểm t1, ta có:
\({i_1} = \frac{{{q_1}\omega }}{{\sqrt 3 }} \Rightarrow \frac{{{{\left( {\frac{{{q_1}\omega }}{{\sqrt 3 }}} \right)}^2}}}{{{\omega ^2}}} + q_1^2 = Q_0^2 \Rightarrow {q_1} = \frac{{{Q_0}\sqrt 3 }}{2}\)
+ Tại thời điểm t1 + Δt, ta có:
\({i_2} = {q_2}\omega \sqrt 3 \Rightarrow \frac{{{{\left( {{q_2}\omega \sqrt 3 } \right)}^2}}}{{{\omega ^2}}} + q_2^2 = Q_0^2 \Rightarrow {q_2} = \frac{{{Q_0}}}{2}\)
+ Trong thời gian Δt điện tích từ q1 đến q2 nhỏ nhất nên:
\(\Delta t = \frac{T}{{12}} = \frac{\pi }{{6\omega }} = \frac{{\pi \sqrt {LC} }}{6}\)

