Đề thi thử THPT QG năm 2021 môn Vật Lý - Trường THPT Tiên Du
Đề thi thử THPT QG năm 2021 môn Vật Lý
-
Hocon247
-
40 câu hỏi
-
90 phút
-
44 lượt thi
-
Trung bình
Tham gia [ Hs Hocon247.com ] - Cộng Đồng Luyện Thi Trực Tuyến để được học tập những kiến thức bổ ích từ HocOn247.com
Trong dao động cưỡng bức, khi xảy ra hiện tượng cộng hưởng thì
Khi xảy ra hiện tượng cộng hưởng, tần số ngoại lực bằng tần số dao động riêng.
Một vật nhỏ dao động điều hòa trên trục \(Ox\) theo phương trình: \(x=A\cos \left( \omega t+\varphi \right)\). Gia tốc của vật có biểu thức là:
Phương trình gia tốc: \(a={x}''=-{{\omega }^{2}}A\cos \left( \omega t+\varphi \right)\)
Vật thực hiện đồng thời hai dao động điều hoà cùng phương cùng tần số có phương trình: \({{x}_{1}}={{A}_{1}}\cos \left( \omega t+{{\varphi }_{1}} \right);{{x}_{2}}={{A}_{2}}\cos \left( \omega t+{{\varphi }_{2}} \right)\). Biên độ A của dao động tổng hợp của hai dao động trên được cho bởi công thức nào sau đây?
Biên độ dao động tổng hợp:
\(A=\sqrt{{{A}_{1}}^{2}+{{A}_{2}}^{2}+2{{A}_{1}}{{A}_{2}}\cos \left( {{\varphi }_{1}}-{{\varphi }_{2}} \right)}\)
Công thức tính tần số dao động của con lắc lò xo
Công thức tính tần số của con lắc lò xo là:
\(f=\frac{1}{2\pi }\sqrt{\frac{g}{\Delta {{\text{l}}_{0}}}}\)
Trong dao động tắt dần chậm đại lượng không đổi theo thời gian là
Dao động tắt dần có chu kì không đổi theo thời gian.
Hai dao động điều hòa cùng phương, cùng tần số được gọi là hai dao động cùng pha nếu độ lệch pha của chúng bằng là
Hai dao động cùng phương, cùng tần số, cùng pha có độ lệch pha: \(\Delta \varphi =k2\pi \)
Véc tơ vận tốc của một vật dao động điều hòa luôn
Vận tốc của vật dao động điều hòa luôn cùng hướng chuyển động.
Một con lắc đơn gồm vật nặng có khối lượng m treo vào sợi dây có chiều dài l ở nơi có gia tốc trọng trường g. Khi vật dao động điều hoa có li độ góc là α thì lực kéo về
Lực kéo về của con lắc đơn: \(F=-mg\alpha \)
Con lắc đơn có cấu tạo gồm
Cấu tạo con lắc đơn gồm: một vật nặng treo vào một sợi dây nhẹ, không dãn vào một điểm cố định.
Nguyên nhân gây ra dao động tắt dần của con lắc lò xo dao động trên mặt phẳng nằm ngang là
Nguyên nhân gây ra dao động tắt dần của con lắc lò xo trên mặt phẳng ngang là do ma sát giữa vật và mặt phẳng ngang.
Một vật dao động điều hòa theo phương trình \(x=A\cos \left( \omega t+\varphi \right)\) với \(A>0;\omega >0\). Đại lượng A được gọi là:
Phương trình dao động điều hòa \(x=A\cos \left( \omega t+\varphi \right)\) với A là biên độ dao động
Một con lắc lò xo đang dao động điều hòa, đại lượng nào sau đây của con lắc được bảo toàn?
Trong dao động điều hòa của con lắc lò xo, cơ năng luôn được bảo toàn.
Dao động của đồng hồ quả lắc là:
Dao động của đồng hồ quả lắc là dao động duy trì.
Một vật dao động điều hoà với biên độ A tần số góc ω, gia tốc cực đại là
Gia tốc cực đại của dao động điều hòa: \({{a}_{\max }}={{\omega }^{2}}A\)
Một con lắc lò xo gồm lò xo và vật nhỏ có khối lượng m đang dao động điều hòa theo phương nằm ngang. Khi vật có tốc độ v thì động năng của con lắc được tính bằng công thức nào sau đây?
Động năng của con lắc lò xo: \({{W}_{d}}=\frac{1}{2}m{{v}^{2}}\)
Tại nơi có gia tốc trọng trường g, một con lắc đơn có sợi dây dài l đang dao động điều hoà. Chu kì dao động của con lắc là:
Chu kì của con lắc đơn: \(T=2\pi \sqrt{\frac{\text{l}}{g}}\)
Một con lắc đơn dao động theo phương trình \(s=10\cos \left( 2\pi t \right)\left( cm \right)\). Chu kì dao động là
Chu kì dao động của con lắc là: \(T=\frac{2\pi }{\omega }=\frac{2\pi }{2\pi }=1\left( s \right)\)
Một hệ dao động chịu tác dụng của ngoại lực tuần hoàn \({{F}_{n}}={{F}_{0}}\cos 10\pi t\) thì xảy ra hiện tượng cộng hưởng. Tần số dao động riêng của hệ phải là:
Để xảy ra hiện tượng cộng hưởng, tần số của ngoại lực: \(\omega ={{\omega }_{0}}=10\pi \left( rad/s \right)\)
Tần số dao động riêng của hệ là: \({{f}_{0}}=\frac{{{\omega }_{0}}}{2\pi }=\frac{10\pi }{2\pi }=5\left( Hz \right)\)
Một vật thực hiện đồng thời hai dao động điều hòa cùng phương, cùng tần số, có biên độ lần lượt là 8cm và 5cm. Biên độ dao động tổng hợp có thể nhận giá trị bằng:
Biên độ dao động tổng hợp là: \(A=\sqrt{{{A}_{1}}^{2}+{{A}_{2}}^{2}+2{{A}_{1}}{{A}_{2}}\cos \Delta \varphi }\)
Với \(0\le \varphi \le \pi \Rightarrow \left| {{A}_{1}}+{{A}_{2}} \right|\le A\le {{A}_{1}}+{{A}_{2}}\Rightarrow 3\le A\le 13\left( cm \right)\)
→ Biên độ dao động tổng hợp có thể nhận giá trị 10cm.
Một con lắc lò xo có khối lượng \({{T}_{1}}\) dao động điều hòa với biên độ \(A=10cm\), tần số góc \(10rad/s\). Lực kéo về cực đại là
Lực kéo về cực đại tác dụng lên con lắc là: \({{F}_{\max }}=m{{\omega }^{2}}A=0,{{2.10}^{2}}.0,1=2\left( N \right)\)
Một con lắc lò xo, vật nặng có khối lượng \(m=250g\), lò xo có độ cứng \(k=100N/m\). Tần số góc dao động của con lắc là
Tần số góc dao động của con lắc là: \(\omega =\sqrt{\frac{k}{m}}=\sqrt{\frac{100}{0,25}}=20\left( rad/s \right)\)
Cơ năng của một dao động tắt dần chậm giảm 6% sau mỗi chu kì. Sau mỗi chu kì biên độ giảm
Cơ năng ban đầu của con lắc là: \(W=\frac{1}{2}m{{\omega }^{2}}{{A}^{2}}\)
Sau 1 chu kì, cơ năng của con lắc còn lại là:
\({W}'=W-\Delta W=0,94W=0,94.\frac{1}{2}m{{\omega }^{2}}{{A}^{2}}\)
\(\Rightarrow \frac{1}{2}m{{\omega }^{2}}{{{A}'}^{2}}=0,94.\frac{1}{2}m{{\omega }^{2}}{{A}^{2}}\Rightarrow {A}'=\sqrt{0,94}A\approx 0,97A\)
\(\Rightarrow \Delta A=A-{A}'=0,03A=A.3%\)
Hai dao động điều hòa cùng phương, cùng tần số có phương trình \({{x}_{1}}={{A}_{1}}\cos \left( \omega t+\frac{\pi }{6} \right)cm\) và \({{x}_{2}}={{A}_{2}}\cos \left( \omega t+\frac{\pi }{2} \right)cm\). Độ lệch pha của hai dao động là
Độ lệch pha của hai dao động là: \(\Delta \varphi =\left| {{\varphi }_{1}}-{{\varphi }_{2}} \right|=\left| \frac{\pi }{6}-\frac{\pi }{2} \right|=\frac{\pi }{3}\left( rad \right)\)
Một con lắc lò xo, độ cứng của lò xo 9N/m, khối lượng của vật 1kg dao động điều hoà. Tại thời điểm vật có toạ độ \(2\sqrt{3}cm\) thì vật có vận tốc 6cm/s. Tính cơ năng dao động.
Tần số góc của con lắc là: \(\omega =\sqrt{\frac{k}{m}}=\sqrt{\frac{9}{1}}=3\left( rad/s \right)\)
Áp dụng công thức độc lập với thời gian tại thời điểm t, ta có:
\({{x}^{2}}+\frac{{{v}^{2}}}{{{\omega }^{2}}}={{A}^{2}}\Rightarrow {{\left( 2\sqrt{3} \right)}^{2}}+\frac{{{6}^{2}}}{{{3}^{2}}}={{A}^{2}}\Rightarrow A=4\left( cm \right)\)
Cơ năng của con lắc là: \(W=\frac{1}{2}k{{A}^{2}}=\frac{1}{2}.9.0,{{04}^{2}}=7,{{2.10}^{-3}}\left( J \right)=7,2\left( mJ \right)\)
Một vật nhỏ dao động điều hòa với biên độ 3cm. Chiều dài quỹ đạo của vật là
Chiều dài quỹ đạo của vật là: \(L=2A=2.3=6\left( cm \right)\)
Một chất điểm dao động điều hoà với tần số bằng 4Hz và biên độ dao động 10cm. Vận tốc cực đại của chất điểm bằng
Vận tốc cực đại của chất điểm là:
\({{v}_{\max }}=\omega A=2\pi f.A=2\pi .4.10=80\pi \left( cm/s \right)\)
Một vật nhỏ dao động điều hòa có biên độ A. Quãng đường mà vật đi được trong 1 chu kì là:
Quãng đường vật đi được trong 1 chu kì là: \(S=4A\)
Tại một nơi trên mặt đất có \(g=9,87m/{{s}^{2}}\), một con lắc đơn dao động điều hòa với chu kỳ 1s. Chiều dài con lắc là
Chu kì của con lắc là: \(T=2\pi \sqrt{\frac{l}{g}}\Rightarrow l=\frac{g{{T}^{2}}}{4{{\pi }^{2}}}=\frac{9,{{87.1}^{2}}}{4{{\pi }^{2}}}=0,25\left( m \right)\)
Có hai con lắc đơn mà độ dài của chúng khác nhau 22cm, dao động ở cùng một nơi. Trong cùng một khoảng thời gian, con lắc thứ nhất thực hiện được 30 dao động toàn phần, con lắc thứ hai thực hiện được 36 dao động toàn phần. Độ dài của các con lắc nhận giá trị nào sau đây:
Chu kì của hai con lắc là:
\(\left\{ \begin{array}{*{35}{l}} {{T}_{1}}=2\pi \sqrt{\frac{{{l}_{1}}}{g}} \\ {{T}_{2}}=2\pi \sqrt{\frac{{{l}_{2}}}{g}} \\ \end{array} \right.\Rightarrow \frac{{{T}_{2}}}{{{T}_{1}}}=\sqrt{\frac{{{l}_{2}}}{{{l}_{1}}}}\)
Trong cùng một khoảng thời gian, hai con lắc thực hiện được số chu kì là:
\(\left\{ \begin{array}{*{35}{l}} {{n}_{1}}=\frac{\Delta t}{{{T}_{1}}} \\ {{n}_{2}}=\frac{\Delta t}{{{T}_{2}}} \\ \end{array} \right.\)
\(\Rightarrow \frac{{{n}_{1}}}{{{n}_{2}}}=\frac{{{T}_{2}}}{{{T}_{1}}}=\sqrt{\frac{{{l}_{2}}}{{{l}_{1}}}}\Rightarrow \frac{{{l}_{2}}}{{{l}_{1}}}={{\left( \frac{{{n}_{1}}}{{{n}_{2}}} \right)}^{2}}={{\left( \frac{30}{36} \right)}^{2}}=\frac{25}{36}\Rightarrow {{l}_{2}}=\frac{25}{36}{{l}_{1}}\)
Lại có: \({{l}_{1}}-{{l}_{2}}=22\Rightarrow {{l}_{1}}-\frac{25}{36}{{l}_{1}}=22\Rightarrow {{l}_{1}}=72\left( cm \right)\)
\(\Rightarrow {{l}_{2}}=\frac{25}{36}{{l}_{1}}=50\left( cm \right)\)
Chuyển động của một vật là tổng hợp hai dao động điều hòa cùng phương, cùng tần số, có phương trình là: \({{x}_{1}}=4\cos \left( 10t+\frac{\pi }{4} \right)cm;{{x}_{2}}=3\cos \left( 10t-\frac{3\pi }{4} \right)cm\). Gia tốc cực đại là
Độ lệch pha giữa hai dao động là: \(\Delta \varphi ={{\varphi }_{1}}-{{\varphi }_{2}}=\frac{\pi }{4}-\left( -\frac{3\pi }{4} \right)=\pi \)
→ Hai dao động ngược pha
Biên độ của dao động tổng hợp là: \(A=\left| {{A}_{1}}-{{A}_{2}} \right|=\left| 4-3 \right|=1\left( cm \right)\)
Gia tốc cực đại là: \({{a}_{\max }}={{\omega }^{2}}A={{10}^{2}}.1=100\left( cm/{{s}^{2}} \right)=1\left( m/{{s}^{2}} \right)\)
Một chất điểm dao động điều hòa với phương trình \(x=A\cos \left( \omega t+\varphi \right)\) có pha dao động của li độ quan hệ với thời gian theo đồ thị được biểu diễn như hình vẽ. Biết \({{t}_{2}}-{{t}_{1}}=2s\). Tần số góc là
.png)
Từ đồ thị ta thấy pha dao động tại thời điểm \({{t}_{1}}\) và \({{t}_{2}}\) là:
\(\left\{ \begin{array}{*{35}{l}} {{\varphi }_{1}}=-\frac{\pi }{3}\left( rad \right) \\ {{\varphi }_{2}}=0\left( rad \right) \\ \end{array} \right.\Rightarrow \Delta \varphi ={{\varphi }_{2}}-{{\varphi }_{1}}=\frac{\pi }{3}\left( rad \right)\)
\(\Delta \varphi =\omega \left( {{t}_{2}}-{{t}_{1}} \right)\Rightarrow \omega .2=\frac{\pi }{3}\Rightarrow \omega =\frac{\pi }{6}\left( rad/s \right)\)
Một con lắc lò xo treo vào một điểm cố định, dao động điều hòa theo phương thẳng đứng với chu kì 0,4s, biên độ 8cm. Trong một chu kì, thời gian mà lực đàn hồi ngược chiều lực kéo về là
Chu kì của con lắc là: \(T=2\pi \sqrt{\frac{\Delta l}{g}}\)
\(\Rightarrow \Delta l=\frac{g{{T}^{2}}}{4{{\pi }^{2}}}=\frac{10.0,{{4}^{2}}}{4.{{\pi }^{2}}}=0,04\left( m \right)=4cm\) \(\Rightarrow \Delta l=\frac{A}{2}\)
Ta có VTLG:
.png)
Từ VTLG, ta thấy lực đàn hồi ngược chiều với lực kéo về khi vật có li độ:
\(-\Delta l\le x\le 0\Rightarrow -\frac{A}{2}\le x\le 0\)
Góc quét trong 1 chu kì là: \(\Delta \varphi =2\alpha =2\left( \frac{\pi }{2}-ar\cos \frac{\Delta l}{A} \right)=2.\left( \frac{\pi }{2}-ar\cos \frac{1}{2} \right)=\frac{\pi }{3}\left( rad \right)\)
Thời gian lực đàn hồi ngược chiều lực kéo về trong 1 chu kì là: \(\Delta t=\frac{\Delta \varphi }{\omega }=\frac{\Delta \varphi }{\frac{2\pi }{T}}=\frac{\frac{\pi }{3}}{\frac{2\pi }{0,4}}=\frac{1}{15}\left( s \right)\)
Chuyển động của một vật là tổng hợp của hai dao động điều hòa cùng phương, cùng tần số. Biên độ dao động thứ nhất và dao động tổng hợp là bằng nhau và bằng \(10cm\). Dao động tổng hợp lệch pha \(\frac{\pi }{3}\) so với dao động thứ nhất. Biên độ dao động thứ hai là:
Ta có giản đồ vecto:
.png)
Từ giản đồ vecto, áp dụng định lí hàm cos, ta có:
\({{A}_{2}}^{2}={{A}_{1}}^{2}+{{A}^{2}}-2A.{{A}_{1}}\cos \frac{\pi }{3}\)
\(\Rightarrow {{A}_{2}}^{2}={{10}^{2}}+{{10}^{2}}-2.10.10.\cos \frac{\pi }{3}\)
\(\Rightarrow {{A}_{2}}^{2}=100\Rightarrow {{A}_{2}}=10\left( cm \right)\)
Một vật dao động điều hoà trên trục Ox. Đồ thị biểu diễn sự phụ thuộc vào thời gian của li độ có dạng như hình vẽ bên. Phương trình dao động của li độ là
.png)
Từ đồ thị ta thấy biên độ dao động: \(A=4cm\)
Ở thời điểm đầu, vật có li độ \(x=-2cm=-\frac{A}{2}\) và đang tăng
Ta có VTLG:
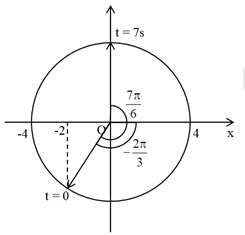
Từ đồ thị ta thấy pha đàu của dao động là: \(\varphi =-\frac{2\pi }{3}\left( rad \right)\)
Ở thời điểm \(t=7s\), vật ở VTCB và đang giảm → pha dao động là: \(\frac{\pi }{2}\left( rad \right)\)
Góc quét từ thời điểm \(t=0\) đến \(t=7s\) là: \(\Delta \varphi =\frac{\pi }{2}-\left( -\frac{2\pi }{3} \right)=\frac{7\pi }{6}\left( rad \right)\)
Tần số góc của dao động là: \(\omega =\frac{\Delta \varphi }{\Delta t}=\frac{\frac{7\pi }{6}}{7}=\frac{\pi }{6}\left( rad/s \right)\)
Phương trình dao động của vật là: \(x=4\cos \left( \frac{\pi }{6}t-\frac{2\pi }{4} \right)\left( cm \right)\)
Một con lắc lò xo nằm ngang gồm vật nhỏ khối lượng 200gam, lò xo có độ cứng \(20N/m\), hệ số ma sát trượt giữa vật và mặt phẳng ngang là 0,1. Ban đầu vật được giữ ở vị trí lò xo dãn 9cm. Độ nén cực đại của lò xo là:
Ban đầu vật ở vị trí lò xo dãn 9cm \(\Rightarrow A=9cm\)
Vật đến vị trí lò xo bị nén cực đại tức là vật đi được nửa chu kì.
.png)
⇒ Độ giảm biên độ sau nửa chu kì: \(\Delta A=\frac{2\mu mg}{k}=\frac{2.0,1.0,2.10}{20}=0,02m=2cm\)
Biên độ dao động của vật sau nửa chu kì: \({A}'=A-\Delta A=9-2=7cm\)
⇒ Độ nén cực đại của lò xo là: \(\Delta {{l}_{nen}}={A}'=7cm\)
Một con lắc đơn gồm quả cầu nhỏ khối lượng m treo vào sợi dây có chiều dài \(l=40cm\). Bỏ qua sức cản không khí. Đưa con lắc lệch khỏi phương thẳng đứng góc \({{\alpha }_{0}}=0,15rad\) rồi thả nhẹ, quả cầu dao động điều hòa. Quãng đường cực đại mà quả cầu đi được trong khoảng thời gian \(\frac{2T}{3}\) là
Biên độ cong: \({{S}_{0}}={{\alpha }_{0}}.l=0,15.40=6cm\)
Có: \(\Delta t=\frac{2T}{3}=\frac{T}{2}+\frac{T}{6}\)
+ Với khoảng thời gian \(\frac{T}{2}\) vật luôn đi được quãng đường là \(2{{S}_{0}}\)
+ Với khoảng thời gian \(\frac{T}{6}\) vật đi được quãng đường lớn nhất khi nó di chuyển gần VTCB. Góc quét được: \({{\varphi }_{\frac{T}{6}}}=\omega .\frac{T}{6}=\frac{2\pi }{T}.\frac{T}{6}=\frac{\pi }{3}\)
Biểu diễn trên VTLG ta có:
.png)
Từ hình vẽ ta tính được quãng đường cực đại mà quả cầu đi được trong \(\frac{2T}{3}\) là:
\(S=2{{S}_{0}}+{{S}_{0}}=3{{S}_{0}}=3.6=18cm\)
Một vật dao động điều hòa với phương trình \(x=10\cos \left( \pi t+\varphi \right)cm\). Khoảng thời gian ngắn nhất giữa hai lần liên tiếp vật cách vị trí cân bằng một khoảng \(a\) bằng với khoảng thời gian ngắn nhất giữa hai lần liên tiếp vật cách vị trí cân bằng một khoảng \(b\) \(\left( b<a<b\sqrt{3} \right)\). Trong một chu kỳ khoảng thời gian mà tốc độ của vật không vượt quá \(\frac{\pi \left( b\sqrt{3}-a \right)}{3}cm/s\) bằng \(\frac{2}{3}s\). Tỉ số giữa a và b gần với giá trị nào nhất sau đây?
+ Ta có VTLG:
.png)
Từ hình vẽ ta có:
\(\left\{ \begin{array}{*{35}{l}} a=A.\sin \frac{\varphi }{2} \\ b=A.\cos \frac{A}{2} \\ \end{array} \right.\Rightarrow {{a}^{2}}+{{b}^{2}}={{A}^{2}}=100\left( c{{m}^{2}} \right)\left( 1 \right)\)
+ Lại có hình vẽ:

Góc quét được sau \(\frac{2}{3}s\) là: \(\Delta \varphi =2\alpha =\omega .\Delta t=\pi .\frac{2}{3}\Rightarrow \alpha =\frac{\pi }{3}\)
Có: \({{v}_{0}}=\omega A.\sin \frac{\alpha }{2}\Leftrightarrow \frac{\pi }{3}.\left( b\sqrt{3}-3 \right)=\pi .10.\sin \frac{\pi }{6}\)
\(\Leftrightarrow b\sqrt{3}-a=15cm\left( 2 \right)\)
Từ (1) và (2) ta có hệ phương trình:
\(\left\{ \begin{array}{*{35}{l}} {{a}^{2}}+{{b}^{2}}=100 \\ b\sqrt{3}-a=15cm \\ \end{array} \right.\)
\( \Leftrightarrow\left\{ \begin{array}{*{35}{l}} a=1,978 \\ b=9,802 \\ \end{array} \right.\Rightarrow \frac{a}{b}=0,2\)
Hai con lắc đơn giống hệt nhau mà các vật nhỏ mang điện tích như nhau, được treo ở một nơi trên mặt đất. Trong mỗi vùng không gian chứa mỗi con lắc có một điện trường đều. Hai điện trường này có cùng cường độ nhưng các đường sức vuông góc với nhau. Giữ hai con lắc ở vị trí các dây treo có phương thẳng đứng rồi thả nhẹ thì chúng dao động điều hòa trong cùng một mặt phẳng với biên độ góc \({{8}^{0}}\) và có chu kì tương ứng là \({{T}_{1}}\) và \({{T}_{2}}={{T}_{1}}+0,25s\). Giá trị của \({{T}_{2}}\) là
Gọi \({{g}_{1}}\) và \({{g}_{2}}\) là gia tốc của hai con lắc khi chịu tác dụng của ngoại lực.
Gọi \({{a}_{1}}\) và \({{a}_{2}}\) là gia tốc do lực điện tác dụng lên con lắc 1 và 2.
.png)
Có \({{a}_{1}}={{a}_{2}}\) vì hai con lắc giống nhau đặt trong cùng điện trường đều: \({{a}_{1}}={{a}_{2}}=\frac{\left| q \right|E}{m}\)
Hai con lắc cùng biên độ nên \(\overrightarrow{{{g}_{1}}}\uparrow \uparrow \overrightarrow{{{g}_{2}}}\)
Có \({{T}_{2}}>{{T}_{1}}\Rightarrow {{g}_{2}}<{{g}_{1}}\)
Xét tam giác ABC có:
\(\left\{ \begin{array}{*{35}{l}} {{q}_{1}}={{q}_{2}} \\ \overrightarrow{{{a}_{1}}}\bot \overrightarrow{{{a}_{2}}} \\ \end{array} \right.\Rightarrow \Delta ABC\) vuông cân.
Tam giác OAC có: \(\widehat{OBA}={{37}^{0}}\Rightarrow \frac{{{g}_{2}}}{\sin 37}=\frac{{{a}_{2}}}{\sin 8}\,\,\left( 1 \right)\)
Tam giác OAC có: \(\frac{{{g}_{1}}}{\sin 127}=\frac{{{a}_{1}}}{\sin 8}\left( 2 \right)\)
Từ (1) và (2) suy ra: \(\frac{{{g}_{1}}}{\sin 127}=\frac{{{g}_{2}}}{\sin 37}\Rightarrow \frac{{{g}_{1}}}{{{g}_{2}}}=\frac{\sin 127}{\sin 37}\)
Mà:
\(\left\{ \begin{array}{*{35}{l}} \frac{{{T}_{1}}}{{{T}_{2}}}=\sqrt{\frac{{{g}_{1}}}{{{g}_{2}}}}=\sqrt{\frac{\sin 127}{\sin 37}}\Rightarrow {{T}_{2}}={{T}_{1}}.\sin \sqrt{\frac{\sin 127}{\sin 37}} \\ {{T}_{2}}={{T}_{1}}+0,25 \\ \end{array} \right.\)
\(\Rightarrow {{T}_{1}}\sin \sqrt{\frac{\sin 127}{\sin 37}}={{T}_{1}}+0,25\Rightarrow {{T}_{1}}=1,645s\)
\(\Rightarrow {{T}_{2}}={{T}_{1}}+0,25=1,645+0,25=1,895s\)
Hai chất điểm dao động điều hòa, cùng phương cùng tần số với li độ lần lượt là \({{x}_{1}}\) và \({{x}_{2}}\). Li độ của hai chất điểm thỏa mãn điều kiện: \(4,5x_{1}^{2}+2x_{2}^{2}=18\left( c{{m}^{2}} \right)\). Tính biên độ dao động tổng hợp của hai dao động trên.
Ta có:
\(4,5x_{1}^{2}+2x_{2}^{2}=18\Leftrightarrow \frac{4,5}{18}x_{1}^{2}+\frac{2}{18}x_{2}^{2}=1\Leftrightarrow \frac{x_{1}^{2}}{4}+\frac{x_{2}^{2}}{9}=1\) \(\Leftrightarrow {{\left( \frac{{{x}_{1}}}{2} \right)}^{2}}+{{\left( \frac{{{x}_{2}}}{3} \right)}^{2}}=1\)
\(\Rightarrow \left\{ \begin{array}{*{35}{l}} {{x}_{1}}\bot {{x}_{2}} \\ {{A}_{1}}=2cm \\ {{A}_{2}}=3cm \\ \end{array} \right.\)
⇒ Biên độ của dao động tổng hợp: \(A=\sqrt{A_{1}^{2}+A_{2}^{2}}=\sqrt{4+9}=\sqrt{13}cm\)
Hai vật A và B có cùng khối lượng 0,5kg và có kích thước nhỏ được nối với nhau bởi sợi dây mảnh nhẹ dài 15cm, hai vật được treo vào lò xo có độ cứng \(k=100N/m\) tại nơi có gia tốc trọng trường \(g=10m/{{s}^{2}}\). Lấy \({{\pi }^{2}}=10\). Khi hệ vật và lò xo đang ở vị trí cân bằng người ta đốt sợi dây nối hai vật và vật B sẽ rơi tự do còn vật A sẽ dao động điều hòa. Lần đầu tiên vật A lên đến vị trí cao nhất thì khoảng cách giữa hai vật bằng bao nhiêu? Biết rằng độ cao đủ lớn.
+ Tại VTCB O của hệ gồm 2 vật A và B lò xo dãn:
\(\Delta l=\frac{\left( {{m}_{A}}+{{m}_{B}} \right).g}{k}=\frac{\left( 0,5+0,5 \right).10}{100}=0,1m=10cm\)
+ Khi dây đứt, tại VTCB của vật A, lò xo dãn:
\(\Delta {{l}_{A}}=\frac{{{m}_{A}}g}{k}=\frac{0,5.10}{100}=0,05m=0,5cm\)
.png)
+ Sau khi đứt dây, vật A dao động điều hòa quanh VTCB \({{O}_{A}}\) , li độ ban đầu của vật (≡ VTCB của hệ ban đầu) cũng là biên độ dao động của A (vì tại đây \({{v}_{A}}=0\)):
\(A=x=\Delta l-\Delta {{l}_{A}}=10-5=5cm\)
Với chu kì: \(T=2\pi \sqrt{\frac{{{m}_{A}}}{k}}=2\pi \sqrt{\frac{0,5}{100}}=\frac{\sqrt{5}}{5}s\)
+ Khi A lên đến vị trí cao nhất ở biên trên thì hết thời gian \(t=\frac{T}{2}=\frac{\sqrt{5}}{10}s\)
Tại thời điểm A ở vị trí cao nhất, B đã đi được quãng đường:
\(S=\frac{1}{2}g{{t}^{2}}=\frac{1}{2}.10.{{\left( \frac{\sqrt{5}}{10} \right)}^{2}}=0,25m=25cm\)
Khoảng cách giữa hai vật: \(d=2A+l+S=2.5+15+25=50cm\)

