Đề thi thử THPT QG năm 2022 môn Vật Lý - Trường THPT Kim Liên
Đề thi thử THPT QG năm 2022 môn Vật Lý
-
Hocon247
-
40 câu hỏi
-
90 phút
-
56 lượt thi
-
Trung bình
Tham gia [ Hs Hocon247.com ] - Cộng Đồng Luyện Thi Trực Tuyến để được học tập những kiến thức bổ ích từ HocOn247.com
Đặt điện áp xoay chiều u = U0cosωt vào hai đầu đoạn mạch gồm điện trở R, cuộn cảm thuần có độ tự cảm L và tụ điện có điện dung C mắc nối tiếp. Tổng trở Z của đoạn mạch là
Tổng trở của đoạn mạch là: \(Z=\sqrt{{{R}^{2}}+{{\left( \omega L-\frac{1}{\omega C} \right)}^{2}}}\)
Chọn B.
Hiện tượng đoản mạch của nguồn điện xảy ra khi
Hiện tượng đoản mạch của nguồn điện xảy ra khi nối hai cực của một nguồn điện bằng dây dẫn có điện trở rất nhỏ
Chọn C.
Một con lắc lò xo dao động điều hoà theo phương thẳng đứng. Trong quá trình dao động của vật, chiều dài của lò xo thay đổi từ 20 cm đến 28 cm. Biên độ dao động của vật là
Chiều dài quỹ đạo chuyển động của con lắc là:
\(L={{l}_{\max }}-{{l}_{\min }}=2A\Rightarrow A=\frac{{{l}_{\max }}-{{l}_{\min }}}{2}=\frac{28-20}{2}=4(\text{cm})\)
Chọn B.
Điện trường xoáy là điện trường
Điện trường xoáy là điện trường có các đường sức là đường cong kín
Chọn A.
Bản chất dòng điện trong chất điện phân là
Bản chất dòng điện trong chất điện phân là dòng ion dương và dòng ion âm chuyển động có hướng theo hai chiều ngược nhau
Chọn A.
Sóng cơ truyền theo một đường thẳng từ M đến N với bước sóng λ. Khoảng cách MN = d. Độ lệch pha ∆φ của dao động tại hai điểm M và N là
Độ lệch pha giữa hai điểm M và N là: \(\Delta \varphi =\frac{2\pi d}{\lambda }\)
Chọn D.
Dao động cơ tắt dần là dao động có
Dao động tắt dần là dao động có biên độ giảm dần theo thời gian.
Chọn A.
Cường độ dòng điện \(i=2\sqrt{2}\cos 100\pi t(A)\) có giá trị hiệu dụng là
Cường độ dòng điện \(i=2\sqrt{2}\cos 100\omega t(A)\) có giá trị hiệu dụng là 2 A
Chọn C.
Đặt điện áp \(u=100\cos \left( 100\pi t+\frac{\pi }{3} \right)(V)\) vào hai đầu đoạn mạch có R, L, C mắc nối tiếp thì dòng điện qua mạch có biểu thức \(i=2\cos \left( 100\pi t-\frac{\pi }{6} \right)(A).\) Độ lệch pha giữa điện áp và cường độ dòng điện là
Độ lệch pha giữa điện áp và cường độ dòng điện là:
\(\Delta \varphi ={{\varphi }_{u}}-{{\varphi }_{i}}=\frac{\pi }{3}-\left( -\frac{\pi }{6} \right)=\frac{\pi }{2}(\text{rad})\)
Chọn C.
Dao động của con lắc đồng hồ khi hoạt động bình thường là
Dao động của con con lắc đồng hồ khi hoạt động bình thường là dao động duy trì
Chọn B.
Độ to của âm gắn liền với
Độ to của âm gắn liền với mức cường độ âm
Chọn C.
Một sóng cơ học lan truyền với tốc độ v, chu kì T, tần số f thì có bước sóng là
Bước sóng của sóng cơ học là: \(\lambda =vT=\frac{v}{f}\)
Chọn D.
Hai điện tích điểm tác điện giữa hai điện tích là q1, q2 trái dấu, đặt cách nhau một khoảng r trong chân không. Độ lớn lực tương tác giữa hai điện tích là
Độ lớn lực tương tác giữa hai điện tích trong chân không là: \(F={{9.10}^{9}}\frac{\left| {{q}_{1}}{{q}_{2}} \right|}{{{r}^{2}}}\)
Chọn B.
Ở Việt Nam, mạng điện xoay chiều dân dụng có điện áp hiệu dụng là
Ở Việt Nam, mạng điện xoay chiều dân dụng có điện áp hiệu dụng là 220 V
Chọn C.
Một con lắc lò xo có vật nhỏ khối lượng m dao động điều hoà theo phương ngang với phương trình x = Acos(ωt+φ). Mốc thế năng ở vị trí cân bằng. Cơ năng của con lắc là
Cơ năng của con lắc là: \(\text{W}=\frac{1}{2}m{{\omega }^{2}}{{A}^{2}}\)
Chọn A.
Đặt điện áp xoay chiều có tần số góc ω vào hai đầu cuộn cảm thuần có độ tự cảm L. Cảm kháng của cuộn cảm này là
Cảm kháng của cuộn dây là: ZL = ωL
Chọn C.
Mạch dao động LC gồm cuộn cảm thuần có độ tự cảm \(\frac{1}{\pi }mH\) và tụ điện có điện dung \(\frac{4}{\pi }nF.\) Tần số dao động riêng của mạch là
Tần số dao động riêng của mạch là:
\(f=\frac{1}{2\pi \sqrt{LC}}=\frac{1}{2\pi .\sqrt{\frac{{{10}^{-3}}}{\pi }\cdot \frac{{{4.19}^{-9}}}{\pi }}}=2,{{5.10}^{5}}(\text{Hz})\)
Chọn D.
Khi con ruồi và con muỗi bay, ta nghe được tiếng vo ve từ muỗi bay mà không nghe được từ ruồi là do
Khi con ruồi và con muỗi bay, ta nghe được tiếng vo ve từ muỗi bay mà không nghe được từ ruồi là do tần số đập cánh của muỗi nằm trong khoảng từ 16 Hz đến 20 000 Hz
Chọn A.
Một con lắc lò xo gồm vật nhỏ nhỏ có khối lượng 100 gam và lò xo nhẹ có độ cứng 40 N/m. Cho con lắc dao động lần lượt dưới tác dụng của ngoại lực: F1 = 2cos5t (N); F2 = 2cos20t (N); F3 = 2cos30t (N) và F4 = 2cos25t (N), trong đó t tính bằng s. Hiện tượng cộng hưởng xảy ra khi con lắc chịu tác dụng của ngoại lực là
Tần số góc của con lắc là: \(\Omega =\sqrt{\frac{k}{m}}=\sqrt{\frac{40}{0,1}}=20(\text{rad/s)}\)
Hiện tượng cộng hưởng xảy ra khi ngoại lực có tần số: ω = Ω = 20 rad/s
→ con lắc chịu tác dụng của ngoại lực F2
Chọn B.
Trong thí nghiệm giao thoa ở mặt nước với hai nguồn kết hợp cùng pha đặt tại A và B, trong khoảng giữa hai nguồn thì
Trong thí nghiệm giao thoa ở mặt nước với hai nguồn cùng pha, số vân cực đại giao thoa luôn bằng số vị trí có phần tử dao động với biên độ cực đại trên đoạn thẳng AB.
Chọn D.
Khi dùng đồng hồ đa năng hiện số để đo điện áp xoay chiều, ta đặt núm xoay ở vị trí
Khi dùng đồng hồ đa năng hiện số để đo điện áp xoay chiều, ta đặt núm xoay ở vị trí ACV
Chọn C.
Một sóng cơ truyền dọc theo trục Ox với phương trình u = 5cos(8πt - 0,04πx) (cm) (x tính bằng cm, t tính bằng s). Li độ của phần tử sóng tại vị trí cách nguồn 25 cm, ở thời điểm t = 3s là
Li độ của phần tử sóng là:
u = 5cos(8πt - 0,04πx) = 5cos(8π.3 - 0,04π.25) = -5 (cm)
Chọn C.
Một vật dao động điều hòa có đồ thị biểu diễn li độ x theo thời gian t như hình bên. Chu kì dao động của vật là
.jpg)
Từ đồ thị ta thấy trong khoảng thời gian từ 10 ms đến 60 ms, vật thực hiện được $\frac{1}{2}$ chu kì:
\(\frac{T}{2}=60-10\Rightarrow T=100(\text{ms})=0,1(s)\)
Chọn C.
Một điện trở 10 Ω có dòng điện xoay chiều chạy qua trong thời gian 30 phút thì nhiệt lượng tỏa ra là 900 kJ. Cường độ dòng điện cực đại chạy qua điện trở là
Nhiệt lượng tỏa ra trên điện trở là:
\(Q={{I}^{2}}Rt\Rightarrow I=\sqrt{\frac{Q}{R.t}}=\sqrt{\frac{{{900.10}^{3}}}{10.30.60}}=\sqrt{50}(A)\)
\(\Rightarrow {{I}_{0}}=I\sqrt{2}=10(A)\)
Chọn D.
Từ thông qua một vòng dây dẫn kín là \(\Phi =\frac{{{2.10}^{-2}}}{\pi }\cos \left( 100\pi t+\frac{\pi }{4} \right)(Wb).\) Biểu thức của suất điện động cảm ứng xuất hiện trong vòng dây là
Suất điện động cảm ứng xuất hiện trong vòng dây là:
\({{e}_{cu}}={\Phi }'=-\frac{{{2.10}^{-2}}}{\pi }\cdot 100\pi \sin \left( 100\pi t+\frac{\pi }{4} \right)=2\sin \left( 100\pi t+\frac{\pi }{4} \right)(V)\)
Chọn B.
Một con lắc đơn có chiều dài 2 m, dao động điều hoà với biên độ góc 0,1 rad. Biên độ dài của con lắc là
Biên độ dài của con lắc là: \({{\text{s}}_{0}}=l.{{\alpha }_{0}}\)= 2.0,1 = 0,2 (m) = 20 (cm)
Chọn D.
Một hạt mang điện tích 4.10-8 C chuyển động với tốc độ 400 m/s trong một từ trường đều theo hướng vuông góc với đường sức từ. Biết cảm ứng từ của từ trường có độ lớn 0,025 T. Lực Lorenxơ tác dụng lên điện tích có độ lớn là
Lực Lorenxơ tác dụng lên điện tích là:
\({{f}_{L}}=\left| q \right|vB\sin \alpha ={{4.10}^{-8}}.400.0,025.\sin {{90}^{0}}={{4.10}^{-7}}(N)\)
Chọn D.
Đặt điện áp xoay chiều vào hai đầu đoạn mạch có R, L, C mắc nối tiếp. Biết điện áp hiệu dụng giữa hai đầu điện trở, cuộn cảm thuần và tụ điện lần lượt là UR = 40 V; UL = 50 V và UC = 80 V. Điện áp cực đại giữa hai đầu đoạn mạch là
Điện áp hiệu dụng giữa hai đầu đoạn mạch là:
\(U=\sqrt{U_{R}^{2}+{{\left( {{U}_{L}}-{{U}_{C}} \right)}^{2}}}=\sqrt{{{40}^{2}}+{{(50-80)}^{2}}}=50(V)\)
\(\Rightarrow {{U}_{0}}=U\sqrt{2}=50\sqrt{2}(V)\)
Chọn B.
Đặt một điện áp xoay chiều vào hai đầu đoạn mạch gồm một điện trở R và cuộn cảm thuần mắc nối tiếp thì cảm kháng của cuộn cảm là \({{Z}_{L}}=R\sqrt{3}.\) Hệ số công suất của đoạn mạch là
Hệ số công suất của đoạn mạch là: \(\cos \varphi =\frac{R}{\sqrt{{{R}^{2}}+Z_{L}^{2}}}=\frac{R}{\sqrt{3{{R}^{2}}+{{R}^{2}}}}=0,5\)
Chọn A.
Một học sinh dùng bộ thí nghiệm con lắc đơn để làm thí nghiệm đo độ lớn gia tốc trọng trường g tại phòng thí nghiệm Vật lí trường THPT Kim Liên. Học sinh chọn chiều dài con lắc là 55 cm, cho con lắc dao động với biên độ góc nhỏ hơn 100 và đếm được 10 dao động trong thời gian 14,925s. Bỏ qua lực cản của không khí. Giá trị của g gần nhất với giá trị nào sau đây?
Chu kì của con lắc là: \(T=\frac{t}{n}=\frac{14,925}{10}=1,4925(s)\)
Lại có: \(T=2\pi \sqrt{\frac{l}{g}}\Rightarrow g=\frac{4{{\pi }^{2}}.l}{{{T}^{2}}}=\frac{4{{\pi }^{2}}.0,55}{1,{{4925}^{2}}}\approx 9,748\left( \text{m/}{{\text{s}}^{\text{2}}} \right)\)
Chọn A.
Đặt điện áp xoay chiều \(u=U\sqrt{2}\cos \omega t\) vào hai đầu đoạn mạch chỉ có tụ điện. Tại thời điểm t1, giá trị tức thời của cường độ dòng điện trong đoạn mạch là 2A và điện áp tức thời giữa hai đầu đoạn mạch bằng 0. Tại thời điểm t2, giá trị tức thời của cường độ dòng điện trong đoạn mạch là 1A và điện áp tức thời giữa hai đầu đoạn mạch là \(2\sqrt{3}\)V. Dung kháng của tụ điện là
Đoạn mạch chỉ chứa tụ điện, áp dụng công thức độc lập với thời gian tại các thời điểm, ta có:
\(\frac{u_{1}^{2}}{U_{0}^{2}}+\frac{i_{1}^{2}}{I_{0}^{2}}=1\Rightarrow \frac{0}{U_{0}^{2}}+\frac{{{2}^{2}}}{I_{0}^{2}}=1\Rightarrow {{I}_{0}}=2(A)\)
\(\frac{u_{2}^{2}}{U_{0}^{2}}+\frac{i_{2}^{2}}{I_{0}^{2}}=1\Rightarrow \frac{{{(2\sqrt{3})}^{2}}}{U_{0}^{2}}+\frac{{{1}^{2}}}{{{2}^{2}}}=1\Rightarrow {{U}_{0}}=4(V)\)
Dung kháng của tụ điện là: \({{Z}_{C}}=\frac{{{U}_{0}}}{{{I}_{0}}}=\frac{4}{2}=2(\Omega )\)
Chọn C.
Theo khảo sát của một tổ chức Y tế, tiếng ồn vượt qua 90 dB bắt đầu gây mệt mỏi, mất ngủ, tổn thương chức năng thính giác, mất thăng bằng cơ thể và suy nhược thần kinh. Tại tổ dân cư 118 phố Đặng Văn Ngữ, thành phố Hà Nội có cơ sở cưa gỗ, khi hoạt động có mức cường độ âm lên đến 110 dB với những hộ dân cách đó chừng 100 m. Tổ dân phố đã có khiếu nại đòi chuyển cơ sở đó ra xa khu dân cư. Để không gây ra các hiện tượng sức khỏe trên với người dân thì cơ sở đó phải cách khu dân cư ít nhất là
Mức cường độ âm tại khu dân cư trức và sau khii chuyển xưởng gỗ là:
\({{L}_{1}}=10\lg \frac{{{I}_{1}}}{{{I}_{0}}}=110(dB)\)
\({{L}_{2}}=10\lg \frac{{{I}_{2}}}{{{I}_{0}}}\le 90(dB)\)
\(\Rightarrow {{L}_{1}}-{{L}_{2}}=10\lg \frac{{{I}_{1}}}{{{I}_{2}}}\ge 20(dB)\Rightarrow \lg \frac{{{I}_{1}}}{{{I}_{2}}}\ge 2\)
Lại có: \(I=\frac{P}{4\pi {{r}^{2}}}\Rightarrow I\sim \frac{1}{{{r}^{2}}}\)
\(\Rightarrow \lg \frac{{{I}_{1}}}{{{I}_{2}}}=\lg \frac{r_{2}^{2}}{r_{1}^{2}}\ge 2\Rightarrow \frac{r_{2}^{2}}{r_{1}^{2}}\ge 100\Rightarrow {{r}_{2}}=10{{r}_{1}}=1000(m)\)
Chọn A.
Một vật dao động là tổng hợp của hai dao động điều hòa cùng phương, cùng tần số có phương trình lần lượt là \({{x}_{1}}=20\cos (\omega t-\pi )(\text{cm})\) và \({{x}_{2}}={{A}_{2}}\cos \left( \omega t-\frac{\pi }{3} \right)(\text{cm}).\) Thay đổi A2 để biên độ dao động tổng hợp có giá trị nhỏ nhất, khi đó lệch pha giữa dao động tổng hợp và dao động thành phần x1 là
Ta có giản đồ vecto:
.jpg)
Từ giản đồ vecto, áp dụng định lí hàm cos, ta có:
\({{A}^{2}}=A_{1}^{2}+A_{2}^{2}+2{{A}_{1}}{{A}_{2}}\cos \frac{2\pi }{3}={{20}^{2}}+A_{2}^{2}-20{{A}_{2}}\)
Đặt \(x={{A}_{2}},\) xét hàm số \(f(x)={{x}^{2}}-20x+{{20}^{2}},\) ta có \(f_{(x)}^{\prime }=2x-20\)
Để \({{A}_{\text{min }\!\!~\!\!\text{ }}}\Rightarrow {{f}_{(x)}}\min \Rightarrow {{\text{f}}_{(x)}}=0\Rightarrow x=10\Rightarrow {{A}_{2}}=10(\text{cm})\)
Khi đó, \({{A}_{\min }}=10\sqrt{3}(\text{cm})\)
Ta có: \(\cos \varphi =\frac{A_{1}^{2}+{{A}^{2}}-A_{2}^{2}}{2A.{{A}_{1}}}=\frac{\sqrt{3}}{2}\Rightarrow \varphi =\frac{\pi }{6}\)
Chọn B.
Đặt điện áp \(u=200\sqrt{2}\cos \left( 100\pi t+\frac{\pi }{4} \right)(V)\)(t tính bằng s) vào hai đầu đoạn mạch gồm điện trở 100 Ω, cuộn cảm thuần có độ tự cảm \(\frac{2}{\pi }H\) và tụ điện có điện dung \(\frac{{{10}^{-4}}}{\pi }F\) mắc nối tiếp. Biểu thức cường độ dòng điện trong đoạn mạch là
Cảm kháng của cuộn dây và dung kháng của tụ điện là:
\(\left\{ \begin{array}{*{35}{l}} {{Z}_{L}}=\omega L=100\pi \cdot \frac{2}{\pi }=200(\Omega ) \\ {{Z}_{C}}=\frac{1}{\omega C}=\frac{1}{100\pi \cdot \frac{{{10}^{-4}}}{\pi }}=100(\Omega ) \\ \end{array} \right.\)
Tổng trở của đoạn mạch là:
\(Z=\sqrt{{{R}^{2}}+{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}}=\sqrt{{{100}^{2}}+{{(200-100)}^{2}}}=100\sqrt{2}(\Omega )\)
Cường độ dòng điện cực đại là: \({{I}_{0}}=\frac{{{U}_{0}}}{Z}=\frac{200\sqrt{2}}{100\sqrt{2}}=2(A)\)
Độ lệch pha giữa điện áp và cường độ dòng điện là:
\(\tan \varphi =\frac{{{Z}_{L}}-{{Z}_{C}}}{R}=\frac{200-100}{100}=1\Rightarrow \varphi =\frac{\pi }{4}(\text{rad})\)
Lại có: \(\varphi ={{\varphi }_{u}}-{{\varphi }_{i}}\Rightarrow {{\varphi }_{i}}={{\varphi }_{u}}-\varphi =\frac{\pi }{4}-\frac{\pi }{4}=0(rad)\)
Vậy biểu thức cường độ dòng điện trong mạch là: i = 2cos100πt (A)
Chọn D.
Một con lắc lò xo gồm lò xo nhẹ có độ cứng 10 N/m và vật nhỏ có khối lượng 100 g dao động điều hòa trên quỹ đạo dài 8 cm. Tại thời điểm t = 0, vật đi qua vị trí có li độ -2 cm theo chiều dương. Phương trình dao động của vật là
Tần số góc của con lắc là: \(\omega =\sqrt{\frac{k}{m}}=\sqrt{\frac{10}{0,1}}=10(\text{rad/s)}\)
Chiều dài quỹ đạo dao động của con lắc là:
\(L=2A\Rightarrow A=\frac{L}{2}=\frac{8}{2}=4(\text{cm})\)
Li độ và vận tốc của vật ở thời điểm t = 0 là:
\(\left\{ \begin{array}{*{35}{l}} x=4\cos \varphi =-2 \\ v=-40\sin \varphi >0 \\ \end{array}\Rightarrow \left\{ \begin{array}{*{35}{l}} \cos \varphi =-\frac{1}{2} \\ \sin \varphi <0 \\ \end{array} \right. \right.\Rightarrow \varphi =-\frac{2\pi }{3}(\text{rad})\)
Phương trình dao động của vật là: \(x=4\cos \left( 10t-\frac{2\pi }{3} \right)(\text{cm})\)
Chọn A.
Một sóng cơ hình sin truyền trên sợi dây rất dài có tần số 10 Hz, theo phương ngang. Ở một thời điểm, hình dạng một phần của sợi dây có dạng như hình bên. Biết hai vị trí cân bằng A, C cách nhau một 20 cm, phần tử B đang có xu hướng đi xuống. Sóng truyền theo chiều từ
.jpg)
Ta có hình vẽ biểu diễn mối liên hệ giữa chiều truyền sóng và chiều dao động của phần tử môi trường:
.jpg)
Điểm B đang có xu hướng đi xuống → sóng truyền từ phải qua trái
Từ hình vẽ ta thấy hai điểm A, C dao động ngược pha và gần nhau nhất, khoảng cách AC là:
\(AC=\frac{\lambda }{2}=20(\text{cm})\Rightarrow \lambda =40(\text{cm})\)
Vận tốc truyền sóng là: v = λf = 40.10 = 400 (cm/s) = 4 (m/s)
Chọn C.
Đặt điện áp u = U0cosωt vào hai đầu đoạn mạch như hình bên. Biết tụ điện có điện dung C thay đổi được. Đồ thị hình bên mô tả số chỉ của vôn kế V1 và vôn kế V2 tương ứng là UV1 và UV2 phụ thuộc vào điện dung C. Biết U3 = 2U2. Tỉ số \(\frac{{{U}_{2}}}{{{U}_{4}}}\) là
.jpg)
Từ đồ thị ta thấy khi \({{Z}_{C}}={{Z}_{C1}}\Rightarrow {{U}_{V1\max }}={{U}_{3}}=U\to \) mạch có cộng hưởng: ZL = ZC1
Khi đó: \({{U}_{V2}}={{U}_{C}}={{U}_{2}}\Rightarrow \frac{U{{Z}_{C1}}}{R}={{U}_{2}}\)
Ta có: \({{U}_{3}}=2{{U}_{2}}\Rightarrow U=2\frac{U.{{Z}_{C1}}}{R}\Rightarrow R=2{{Z}_{C1}}=2{{Z}_{L}}\)
\(\Rightarrow {{U}_{2}}=\frac{U{{Z}_{C1}}}{R}=\frac{U.{{Z}_{L}}}{R}=\frac{U}{2}\)
Khi \({{Z}_{C}}={{Z}_{C2}}\Rightarrow {{U}_{V2\max }}={{U}_{C\max }}={{U}_{4}}\Rightarrow {{U}_{4}}=\frac{U\sqrt{{{R}^{2}}+Z_{L}^{2}}}{R}\)
\(\Rightarrow {{U}_{4}}=\frac{U\sqrt{{{R}^{2}}+Z_{L}^{2}}}{R}=\frac{U.\sqrt{4Z_{L}^{2}+Z_{L}^{2}}}{2{{Z}_{L}}}=\frac{U\sqrt{5}}{2}\)
\(\Rightarrow \frac{{{U}_{2}}}{{{U}_{4}}}=\frac{\frac{U}{2}}{\frac{U\sqrt{5}}{2}}=\frac{1}{\sqrt{5}}\)
Chọn D.
Đặt điện áp \(u=220\sqrt{2}\cos (100\pi t+\varphi )(V)\) vào hai đầu đoạn mạch AB như hình bên. Biết hộp X là đoạn mạch có R, L, C mắc nối tiếp; cường độ dòng điện hiệu dụng trong mạch là \(2\sqrt{2}\text{A}\)và R = \(20\sqrt{2}\Omega \text{.}\) Tại thời điểm t (s) cường độ dòng điện trong mạch bằng 4 A. Đến thời điểm \(t+\frac{1}{300}(s)\) thì điện áp u = 0 và đang giảm. Công suất của đoạn mạch X là
.jpg)
Hai thời điểm lệch pha nhau là: \(\Delta \varphi =\omega \Delta t=100\pi .\frac{1}{300}=\frac{\pi }{3}(rad)\)
Ở thời điểm t, cường độ dòng điện trong mạch: I = 4 (A) = I0
Ta có vòng tròn lượng giác:
.jpg)
Tại thời điểm \(t+\frac{1}{300}s,\)điện áp giữa hai đầu đoạn mạch bằng 0 và đang giảm
→ trục u lệch pha \(\frac{\pi }{6}\) so với trục i \(\Rightarrow \varphi =\frac{\pi }{6}\)
Công suất tiêu thụ của đoạn mạch là:
\(P=UI\cos \varphi =220.2\sqrt{2}.\cos \frac{\pi }{6}=538,9(\text{W})\)
Công suất tiêu thụ của đoạn mạch X là:
\({{P}_{X}}=P-{{I}^{2}}{{R}_{1}}=538,9-{{(2\sqrt{2})}^{2}}.20\sqrt{2}=312,6(\text{W})\)
Chọn A.
Trên một sợi dây đàn hồi đang có sóng dừng ổn định với khoảng cách giữa hai nút sóng liên tiếp là 6 cm. Trên dây các phần tử sóng dao động với tần số 5 Hz và biên độ lớn nhất là 3 cm. Gọi N là vị trí của một nút sóng, C và D là hai phần tử trên dây ở hai bên của N và có vị trí cân bằng cách N lần lượt là 10,5 cm và 7,0 cm. Tại thời điểm t1 (s), phần tử C có li độ 1,5 cm và đang hướng về vị trí cân bằng. Vào thời điểm \({{t}_{2}}={{t}_{1}}+\frac{85}{40}(s),\) phần tử D có li độ là
Giả sử tại điểm N là nút sóng thứ 0
Điểm C cách điểm N 10,5 cm thuộc bó sóng thứ 2 sang bên trái
Điểm D cách điểm N 7 cm thuộc bó sóng thứ 2 sang bên phải
→ điểm C thuộc bó sóng chẵn thì điểm D thuộc bó sóng lẻ
→ hai điểm C, D dao động ngược pha
Khoảng cách giữa hai nút sóng liên tiếp là:
\(\frac{\lambda }{2}=6(\text{cm})\Rightarrow \lambda =12(\text{cm})\)
Biên độ của hai điểm C, D lần lượt là:
\(\left\{ \begin{array}{*{35}{l}} {{A}_{C}}=A\sin \left| \frac{2\pi {{d}_{C}}}{\lambda } \right|=3\sin \left| \frac{2\pi .10,5}{12} \right|=1,5\sqrt{2}(\text{cm}) \\ {{A}_{D}}=A\sin \left| \frac{2\pi {{d}_{D}}}{\lambda } \right|=3\sin \left| \frac{2\pi .7}{12} \right|=1,5(\text{cm}) \\ \end{array} \right.\)
Thời gian \(\frac{85}{40}s\) ứng với góc quét là:
\(\Delta \varphi =\omega \Delta t=2\pi f.\Delta t=2\pi .5\cdot \frac{85}{40}=\frac{85\pi }{4}=\frac{5\pi }{4}(\text{rad})\)
Ở thời điểm t1, điểm C có li độ 1,5 cm và đang hướng về vị trí cân bằng
Ta có vòng tròn lượng giác:
.jpg)
Từ đồ thị ta thấy tại thời điểm t2, điểm D có li độ bằng 0 và đang giảm
Hai chất điểm có cùng khối lượng, dao động điều hòa trên hai đường thẳng song song, có vị trí cân bằng cùng thuộc một đường thẳng vuông góc với các quỹ đạo. Đồ thị biểu diễn sự phụ thuộc của li độ x1 và x2 của hai chất điểm theo thời gian t như hình bên. Kể từ t = 0, thời điểm hai chất điểm có cùng li độ lần thứ 2021 thì tỉ số động năng của hai chất điểm \(\frac{{{\text{W}}_{d2}}}{{{\text{W}}_{d1}}}\) là
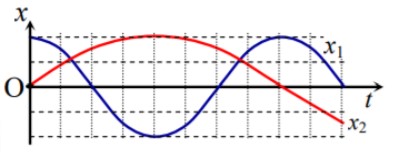
Từ đồ thị ta thấy hai chất điểm có biên độ bằng nhau và bằng A
Chu kì dao động của chất điểm thứ 2: \({{T}_{2}}=2{{T}_{1}}\Rightarrow {{\omega }_{2}}=\frac{{{\omega }_{1}}}{2}\)
Hai chất điểm có cùng li độ x1 = x2, ta có:
\(\frac{{{\text{W}}_{d2}}}{{{\text{W}}_{d1}}}=\frac{\frac{1}{2}m\omega _{2}^{2}\left( {{A}^{2}}-x_{2}^{2} \right)}{\frac{1}{2}m\omega _{1}^{2}\left( {{A}^{2}}-x_{1}^{2} \right)}=\frac{\omega _{2}^{2}}{\omega _{1}^{2}}=\frac{1}{4}=0,25\)
Chọn B.

