+ Lực kéo về biến thiên cùng tần số nhưng ngược pha với li độ, F =  - kx.

Đáp án C

+ Biên độ dao động tổng hợp của vật \(A = \frac{{{v_{max}}}}{{2\pi f}} = \frac{{80\pi \sqrt 7 }}{{20\pi }} = 4\sqrt 7 \)cm.

+ Áp dụng kết quả tổng hợp dao động, ta có:

\({A^2} = A_1^2 + A_2^2 + 2{A_1}{A_2}\cos \Delta \varphi \Rightarrow \cos \Delta \varphi = \frac{{{A^2} - A_1^2A_2^2}}{{2{A_1}{A_2}}} = \frac{{{{\left( {4\sqrt 7 } \right)}^2} - {4^2} - {{\left( {4\sqrt 3 } \right)}^2}}}{{2.4.4\sqrt 3 }} = \frac{{\sqrt 3 }}{2} \Rightarrow \Delta \varphi = \frac{\pi }{6}\)

Đáp án C

+ Vận tốc truyền sóng trên dây \(v = \frac{s}{t} = 0,5\)m.

Bước sóng của sóng \(\lambda  = \frac{v}{f} = \frac{{0,5}}{{10}} = 5\)cm.

Đáp án D

+ Ta có \(f \sim \frac{1}{{\sqrt m }} \Rightarrow \) tăng khối lượng thì tần số của vật sẽ giảm.

Đáp án C

+ Gia tốc của vật có độ lớn cực đại khi vật ở vị trí biên, tại vị trí này thế năng của vật là cực đại.

Đáp án A

+ Tần số của dao động tổng hợp luôn bằng tần số của hai dao động thành phần.

Đáp án A

+ Tần số dao động của con lắc chỉ phụ thuộc vào đặc tính của hệ.

Đáp án D

+ Tỉ số giữa động năng và thế năng của vật \(\frac{{{E_d}}}{{{E_t}}} = \frac{{{A^2} - {x^2}}}{{{x^2}}} = \frac{{1 - 0,{2^2}}}{{0,{2^2}}} = 24\).

Đáp án D

+ Khoảng cách giữa hai ngọn sóng liên tiếp bằng một bước sóng λ = 2 m.

+ 6 ngọn sóng đi qua trong 8 s ứng với 5T = 8\( \Rightarrow T = 1,6\)s.

Vận tốc truyền sóng \(v = \frac{\lambda }{T} = 1,25\) m/s.

Đáp án B

+ Quãng đường vật đi được trong nửa chu kì là S = 2A = 18 cm, vậy A = 9 cm.

Đáp án C

+ Khi sóng truyền đi thì tần số của sóng luôn không đổi theo thời gian.

Đáp án D

+ Chu kì dao động của con lắc \(T = 2\pi \sqrt {\frac{{\Delta {l_0}}}{g}} = \frac{\pi }{{10}}s\)

Đáp án C

+ Công thức liên hệ giữa bước sóng λ, vận tốc truyền sóng v và tần số f: \(\lambda = \frac{v}{f}\).

Đáp án D

+ Tỉ số giữa tốc độ cực đại của các phần tử môi trường và vận tốc truyền sóng là:

\(\delta = \frac{{\omega A}}{v} = \frac{{2\pi fA}}{v} = \frac{{2\pi A}}{\lambda }\).

Đáp án B

+ Chu kì dao động của vât \(T = 2{T_{{E_t}}} = \frac{\pi }{{10}} \Rightarrow \omega  = 20\) rad/s.

Biên độ dao động của vật \(A = \sqrt {\frac{{2E}}{{m{\omega ^2}}}}  = 5\) cm.

Đáp án D

+ Khoảng cách giữa hai điểm gần nhau nhất mà phần tử môi trường tại đó dao động vuông pha nhau là \(\Delta x = \frac{\lambda }{4} = 12,5\) cm.

Đáp án A

+ Trong sóng cơ, tốc độ truyền sóng là tốc độ lan truyền dao động trong môi trường.

Đáp án D

+ Ta có \({E_1} = {E_2} \Leftrightarrow {l_1}\alpha _{01}^2 = {l_2}\alpha _{02}^2 \Rightarrow {\alpha _{02}} = \sqrt {\frac{{{l_1}}}{{{l_2}}}} {\alpha _{01}} = 4,{5^0}\).

Đáp án B

+ Biểu thức liên hệ giữa gia tốc a và li độ x trong dao động điều hòa \(a = - {\omega ^2}x\).

Đáp án B

+ Tốc độ dao động cực đại của vật v_max = ωA = 10π cm/s.

Đáp án A

+ Khoảng cách giữa hai gợn lồi liên tiếp đúng bằng một bước sóng \(\lambda  = \frac{v}{f} = 3\)cm.

Đáp án C

+ Biên độ của dao động tổng hợp không phụ thuộc vào tần số của dao động thành phần.

Đáp án D

+ Dao động của con lắc là dao động tuần hoàn.

Đáp án C

+ Từ phương trình sóng, ta có:

\(\left\{ \begin{array}{l}
\omega  = 2\pi \\
\frac{{2\pi }}{\lambda } = 4\pi 
\end{array} \right. \Rightarrow \left\{ \begin{array}{l}
T = 1\\
\lambda  = 0,5
\end{array} \right. \Rightarrow v = \frac{\lambda }{T} = 0,5\) m/s.

Đáp án A

+ Khi một vật dao động cưỡng bức thì tần số của dao động cưỡng bức đúng bằng tần số của ngoại lực cưỡng bức.

Đáp án A

+ Dao động của con lắc trong trường hợp này là dao động cưỡng bức.

Đáp án C

+ Độ lệch pha giữa hai điểm M, N: \(\Delta \varphi  = \frac{{2\pi \Delta x}}{\lambda } = \frac{{2\pi \Delta x}}{{vT}} = \frac{\pi }{3}\) rad.

Đáp án B

+ Để phân biệt sóng ngang hay sóng dọc người ta dựa vào phương dao động của các phần tử và phương truyền sóng.

Đáp án C

+ Ta có: \(\left\{ \begin{array}{l} {a_{max}} = {\omega ^2}A = 86,4\\ {v_{max}} = \omega A = 2,16 \end{array} \right. \Rightarrow A = 5,4\)cm.

Chiều dài quỹ đạo L = 2A = 10,8 cm.

Đáp án D

+ Khi chất điểm dao động điều hòa đến vị trí cân bằng thì động năng của vật cực đại.

Đáp án C

+ Khi pha dao động của vật là 0,5π → x = 0, vật đi qua vị trí cân bằng, tốc độ của vật là cực đại \(A = \frac{{\left| {{v_0}} \right|}}{\omega } = \frac{{20\sqrt 3 }}{\pi }\) cm.

Động năng của vật khi vật có li độ x = 3π cm.

\({E_d} = E - {E_t} = \frac{1}{2}k\left( {{A^2} - {x^2}} \right) = 0,03\) J.

Đáp án D

+ Với hai dao động vuông pha, ta luôn có \({\left( {\frac{{{x_1}}}{{{A_1}}}} \right)^2} + {\left( {\frac{x}{A}} \right)^2} = 1 \Leftrightarrow {\left( {\frac{{{x_1}}}{6}} \right)^2} + {\left( {\frac{x}{A}} \right)^2} = 1\).

+ Khi dao động thứ hai có li độ bằng biên độ thứ nhất x₂ = 6 cm, dao động tổng hợp có li độ x = 9 cm\( \Rightarrow {x_1} = 9 - 6 = 3\)cm.

Thay vào phương trình độc lập \({\left( {\frac{3}{6}} \right)^2} + {\left( {\frac{9}{A}} \right)^2} = 1 \Rightarrow A = 6\sqrt 3 \) cm.

Đáp án D

+ Biên độ dao động của viên bi cực đại khi xảy ra cộng hưởng \(f = \frac{1}{{2\pi }}\sqrt {\frac{k}{m}} \Rightarrow m = \frac{k}{{{{\left( {2\pi f} \right)}^2}}} = 20\) g.

Đáp án D

+ Ta thấy rằng trong khoảng thời gian Δt = 0,1 s. Sóng truyền đi được quãng đường là \(\frac{\lambda }{{12}} \Rightarrow T = 12.0,1 = 1,2\)s.

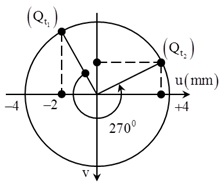
+ Tần số của sóng \(\omega  = \frac{{2\pi }}{T} = \frac{{5\pi }}{3}\) rad/s.

+ Tại thời điểm t = 1 s, điểm Q đi qua vị trí có li độ u =  - 2 cm theo chiều âm. Đến thời điểm  t₃ = t₁ + 0,9 s tương ứng với góc quét \(\Delta \varphi  = \omega \left( {{t_3} - {t_1}} \right) = \frac{{3\pi }}{2}\) rad

Từ hình vẽ, ta xác định được \(v =  - \frac{{{v_{max}}}}{2} =  - \frac{{\omega A}}{2} =  - 1,047\)m/s

Đáp án B

+ Tốc độ của con lắc khi đi qua vị trí cân bằng \({v_0} = {v_{max}} = {\alpha _0}\sqrt {gl} = 0,2\sqrt {10} \)m/s.

+ Tầm ném bay xa của vật theo phương ngang \({x_{max}} = {v_0}t = {v_0}\sqrt {\frac{{2\left( {h - l} \right)}}{g}} = 0,4\sqrt 2 \)m.

Vậy khoảng cách từ vị trí tuột dây đến vị trí vật chạm đất là \(d = \sqrt {{4^2} + {{\left( {0,4\sqrt 2 } \right)}^2}} \approx 4,03\)m

Đáp án B

+ Khoảng thời gian lò xo giãn gấp 2 lần thời gian lò xo bị nén, vậy \(\left\{ \begin{array}{l} {t_g} = \frac{{2T}}{3}\\ {t_n} = \frac{T}{3} \end{array} \right. \Rightarrow A = 2\Delta {l_0} = 5\) cm.

Đáp án C

+ Gia tốc của vật có độ lớn nhỏ nhất khi vật đi qua vị trí cân bằng:

\(\frac{T}{P} = \frac{{mg\left( {3 - 2\cos {\alpha _0}} \right)}}{{mg}} = 2\).

Đáp án D

+ Từ đồ thị, ta có \(T = 3\left( {\frac{{25}}{6} - \frac{5}{6}} \right) = \frac{{20}}{3} \Rightarrow \omega  = \frac{{3\pi }}{{10}}\) rad/s.

+ Biên độ dao động của vật A = 8 cm.

+ Thời điểm \(t = \frac{5}{6}\) s, vật đi qua vị trí biên âm, thời điểm t = 0 tương ứng với góc lùi Δφ = ωΔt = 0,25π rad.

Vậy \(x = 8\cos \left( {\frac{{3\pi }}{{10}}t + \frac{{3\pi }}{4}} \right)\) cm

Đáp án D

+ Ta có tỉ số: \(\frac{{{F_{d{h_{max}}}}}}{{{F_{p{h_{max}}}}}} = \frac{{\Delta {l_0} + A}}{A} \Leftrightarrow \frac{{\Delta {l_0} + 2}}{2} = 4 \Rightarrow \Delta {l_0} = 6\) cm.

Chu kì dao động của con lắc \(T = 2\pi \sqrt {\frac{{\Delta {l_0}}}{g}}  = 2\pi \sqrt {\frac{{{{6.10}^{ - 2}}}}{{10}}}  = 0,49\) s.

Đáp án B

+ Ta có \({a_{1max}} = {\omega ^2}{A_1} = 7,5 \Rightarrow \omega  = 5\pi \) rad/s.

+ Xét dao động (1). Tại thời điểm \(t = \frac{7}{{20}}\)s, chất điểm đang ở vị trí biên dương. Thời điểm t = 0 ứng với góc lùi \(\Delta {\varphi _1} = \omega t = \frac{{7\pi }}{4}\) rad.

Từ hình vẽ ta xác định được \({x_1} = 3\cos \left( {5\pi t + \frac{\pi }{4}} \right)\)cm.

+ Với dao động (2). Tại thời điểm \(t = \frac{1}{6}\)s, chất điểm đang đi qua vị trí cân bằng theo chiều âm. Thời điểm t = 0 ứng với góc lùi \(\Delta {\varphi _2} = \omega t = \frac{{5\pi }}{6}\)rad.

Từ hình vẽ, ta xác định được \({x_2} = 6\cos \left( {5\pi t - \frac{\pi }{3}} \right)\)cm.

+ Khoảng cách lớn nhất giữa hai chất điểm theo phương Ox: \({d_x} = \sqrt {A_1^2 + A_2^2 - 2{A_1}{A_2}\cos \left( {\Delta \varphi } \right)}  \approx 7,37\)cm

Khoảng cách lớn nhất giữa hai chất điểm \({d_{max}} = \sqrt {{5^2} + 7,{{37}^2}}  = 8,9\)cm

Đáp án D