Tần số âm cơ bản do dây đàn phát ra là \({f_0} = \frac{v}{{2l}} = \frac{{450}}{{2.1}} = 225Hz\)

Ta có

\(\eqalign{ & \left\{ \matrix{ {1 \over 2}k{x^2} + 0,48 = {1 \over 2}k{A^2} \hfill \cr {1 \over 2}k{\left( {3x} \right)^2} + 0,32 = {1 \over 2}k{A^2} \hfill \cr} \right. = > {1 \over 2}k{x^2} = 0,02J = > k = 100N/m \cr & = > {1 \over 2}k{A^2} = 0,5J = > A = 0,1m = 10cm \cr} \)

Để người ngoài bể không quan sát thấy viên kim cương thì tia sáng từ viên kim cương đến rìa cảu tấm bè bị phạ xạ toàn phần không cho tia khúc xạ ra ngoài không khí

Góc tới giới hạn ứng với cặp môi trường nước và không khí là \(\sin {i_{gh}} = \frac{{{n_2}}}{{{n_1}}} = \frac{3}{4}\)

Ta có \(\tan {i_{gh}} = \frac{{{R_{\min }}}}{h} = > {R_{\min }} = h\tan {i_{gh}} = 2,27m\)

\(\frac{{u_C^2}}{{U_{0C}^2}} + \frac{{u_R^2}}{{U_{0R}^2}} = 1\)

Đáp án C

Dung kháng và cường độ dòng điện cực đại qua mạch là \({Z_C} = \frac{1}{{\omega C}} = \frac{1}{{100\pi .\frac{{{{10}^{ - 4}}}}{\pi }}} = 100\Omega = > {I_0} = \frac{{{U_0}}}{{{Z_C}}} = \frac{{120\sqrt 2 }}{{100}} = 1,2\sqrt 2 \Omega \)

Vì trong mạch chỉ chứ tụ nên i sớm pha hơn u góc \(\frac{\pi }{2}\) vậy pha ban đầu của i là \({\varphi _i} = \frac{\pi }{6} + \frac{\pi }{2} = \frac{{2\pi }}{3}\)

Dòng điện qua mạch có biểu thức là \(i = 1,2\sqrt 2 \cos \left( {100\pi  + \frac{{2\pi }}{3}} \right)A\)

M và N là hai đỉnh sóng mà giữa chúng còn 1 đỉnh sóng nữa vậy khoảng cách giữa M và N là 2 bước sóng

Cảm kháng, dung kháng và tổng trở của toàn mạch là

\(\eqalign{ & {Z_L} = \omega .L = 100\pi .{1 \over \pi } = 100\Omega ;{Z_C} = {1 \over {\omega C}} = {1 \over {100\pi .{{{{10}^{ - 3}}} \over {6\pi }}}} = 60\Omega \cr & = > Z = \sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} = \sqrt {{{40}^2} + {{\left( {100 - 60} \right)}^2}} = 40\sqrt 2 \Omega \cr} \)

Cường độ dòng điện cực đại qua mạch là \({I_0} = \frac{{{U_0}}}{Z} = \frac{{120}}{{40\sqrt 2 }} = 1,5\sqrt 2 A\)

Độ lệch pha giữ u và i là \(\tan \varphi  = \frac{{{Z_L} - {Z_C}}}{R} = \frac{{100 - 60}}{{40}} = 1;{Z_L} > {Z_C} =  > \varphi  = \frac{\pi }{4} =  > {\varphi _i} = \frac{\pi }{3} - \frac{\pi }{4} = \frac{\pi }{{12}}\)

Biểu thức cường độ dòng điện trong mạch là \(i = 1,5\sqrt 2 \cos \left( {100\pi  + \frac{\pi }{{12}}} \right)A\)

Dòng điện Phu-cô là dòng điện cảm ứng sinh ra trong khối vật dẫn khi khối vật dẫn chuyển động cắt các đường sức từ.

\(P = \frac{{{U^2}}}{R}cos\varphi\)   

Đáp án B

Đáp án B

Mắt không có tật là mắt khi không điều tiết có tiêu điểm nằm trên màng lưới

Đáp án A

Khi R biến thiên để công suất tiêu thụ trên biến trở là cực đại, ta có

\(R = {R_0} = \sqrt {{r^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}}  =  > {Z^2} = {\left( {{R_0} + r} \right)^2} + {\left( {{Z_L} - {Z_C}} \right)^2} = 2{R_0}\left( {r + {R_0}} \right)(1)\)

Công suất tiêu thụ trên mạch khi đó là \({P_{AB}} = \frac{{{U^2}}}{{{Z^2}}}\left( {{R_0} + r} \right) = \frac{{{U^2}}}{{2{R_0}}} \Leftrightarrow 90 = \frac{{{{120}^2}}}{{2{R_0}}} =  > {R_0} = 80\Omega \)

Kết hợp với giải thuyết: \({U_{AM}} = \frac{{U\sqrt {{r^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }}{Z} = U\frac{{{R_0}}}{Z} \Leftrightarrow 40\sqrt 3  = 120\frac{{80}}{Z} =  > Z = 80\sqrt 3 \Omega \)

Thay vào (1) ta tìm được \(r = 40\Omega \)

Vậy công suất tiêu thụ trên MB là \({P_{MB}} = \frac{{{U^2}}}{{{Z^2}}}r = 30W\)

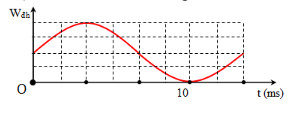
Dựa vào đồ thị

\(\begin{array}{l}
3.\frac{{T'}}{4} = {10.10^{ - 3}}s \to T' = \frac{{40}}{m}{.10^{ - 3}}s\\
 \to T = 2T' = \frac{{80}}{3}{.10^{ - 3}}s \to f = \frac{1}{T} = 37,5Hz
\end{array}\)

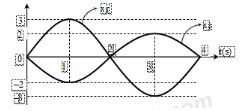
Phương trình dao động của x1, x2 lần lượt là \({x_1} = 3\cos \left( {\frac{\pi }{2}t - \frac{\pi }{2}} \right)cm;{x_2} = 2\cos \left( {\frac{\pi }{2}t + \frac{\pi }{2}} \right)\)

Phương trình dao động tổng quát của x là \(x = {x_1} + {x_2} = 1\cos \left( {\frac{\pi }{2}t - \frac{\pi }{2}} \right)cm\)

Phương trình vận tốc của chất điểm là \(v = x' = \frac{\pi }{2}\cos \frac{\pi }{2}t\left( {cm/s} \right)\)

Công suất tiêu thụ của mạch là

\(\eqalign{
& P = UI\cos \varphi = > U = {P \over {I\cos \varphi }} = {{150} \over {\sqrt 3 .\cos {\pi \over 6}}} = 100V \cr
& = > {U_0} = U\sqrt 2 = 100.\sqrt 2 V \cr} \)

Hình B đúng vì trong hình B khi khung dây lại gần nam châm thì số đường sức từ qua khung tăng lên (B tăng); dòng cảm ứng có chiều làm giảm sự tăng nên cảm ứng từ do khung dây gây ra có chiều từ phải sang trái. (do cảm ứng từ cyar nam châm đi ra từ cực Bắc).

Áp dụng quy tắc nắm tay phải xác định được chiều dòng điện cùng chiều kim đồng hồ.

Chọn C

Đáp án C

Do \({\varphi _1} + {\varphi _2} = {90^0}\;$$ nên ta có: $$x = {Z_{L1}} - {Z_C} = \frac{{{R^2}}}{{{Z_C} - {Z_{L2}}}} = \frac{{{R^2}}}{y}\left( 1 \right)\,\,\,\,\left( {y = {Z_C} - {Z_{L2}}} \right)$ \)

\(\eqalign{ & {U_{MB1}} = {{180x} \over {\sqrt {\left( {{R^2} + {x^2}} \right)} }} = U;{U_{MB2}} = {{180y} \over {\sqrt {\left( {{R^2} + {y^2}} \right)} }} = \sqrt 3 U \cr & = > {x \over y}.{{\sqrt {\left( {{R^2} + {y^2}} \right)} } \over {\sqrt {\left( {{R^2} + {x^2}} \right)} }} = {1 \over {\sqrt 3 }}\left( 2 \right) \cr} \)

Từ (1) và (2) ta được  U = 90V

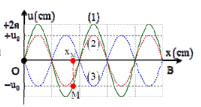
Đáp án C

Chu kỳ sóng là \(\frac{T}{8} = 0,005s =  > T = 0,04s =  > \lambda  = v.T = 16cm\)

${u_0} = \sqrt 2 A$ => M cách nút gần nhất một khoảng \({u_0} = \sqrt 2 A =  > \frac{\lambda }{8} = 2cm\)

Điểm có cùng biên độ với M sẽ nằm ở bó sóng cuối cùng, luôn dao động ngược pha với M. Từ hình vẽ ta có

\({d_{\max }} = \sqrt {{{\left( {2.2\sqrt 2 } \right)}^2} + {{\left( {24} \right)}^2}}  = 24,66cm\)

Khi có góc lệch cực tiểu thì \({i_1} = {i_2} = \frac{{{D_{\min }} + A}}{2},{r_1} = {r_2} = 0,5A\)

Mà \(n = \frac{{\sin \left( {\frac{{{D_{\min }} + A}}{2}} \right)}}{{\sin \frac{A}{2}}};D = A =  > \sqrt 3  = \frac{{\sin A}}{{\sin \frac{A}{2}}} =  > A = {60^0}\)

Đáp án A

+ Ta có Z_C = 40Ω

+ tanφ_AM = \( - \frac{{{Z_C}}}{{{R_1}}} =  - 1 \to {\phi _{AM}} =  - \frac{\pi }{4}\)

+ Từ hình vẽ có: φ_MB = \(\frac{\pi }{3}\)

 tan φ_MB = \(\frac{{{Z_L}}}{{{R_2}}} = \sqrt 3  \to {Z_L} = R_2^{}\sqrt 3 \)

* Xét đoạn mạch AM: \(I = \frac{{{U_{AM}}}}{{{Z_{AM}}}} = \frac{{50}}{{40\sqrt 2 }} = 0,625\sqrt 2 \)

* Xét đoạn mạch MB: \({Z_{MB}} = \frac{{{U_{MB}}}}{I} = 120 = \sqrt {R_2^2 + Z_L^2}  = 2{R_2} \Rightarrow {R_2} = 60;{Z_L} = 60\sqrt 3 \)

Hệ số công suất của mạch AB là :

Cosφ = \(\frac{{{R_1} + {R_2}}}{{\sqrt {{{({R_1} + R{}_2)}^2} + {{(Z_L^{} - {Z_C})}^2}} }}\) » 0,84    

Đáp án D

Tốc độ cực đại của con lắc khi đi qua vị trí cân bằng là \({v_{\max }} = \sqrt {2gl\left( {1 - \cos {\alpha _0}} \right)}  = \sqrt {2.10.1.\left( {1 - \cos 60} \right)}  = \sqrt {10} \left( {m/s} \right)\)

Khi L thay đổi để U_Lmax ta có \({U^2} = {U_L}\left( {{U_L} - {U_C}} \right) = 125.\left( {125 - 80} \right) = {75^2} =  > U = 75V\)

Hiện tượng giao thoa sóng xảy ra khi có hai sóng xuất phát từ hai tâm dao động cùng tần số, cùng pha giao nhau.

Chọn đáp án D

Điện trở của bóng đèn:  \(R = {{U_{dm}^2} \over {{P_{dm}}}} = {{{6^2}} \over 6} = 6W\)

Vì bóng đèn sang bình thường nên  \(I = {I_{dm}} = {{{P_{dm}}} \over {{U_{dm}}}} = {6 \over 6} = 1A\)

Từ công thức  \(I = {E \over {R + r}} \Rightarrow E = I\left( {R + r} \right) = 1\left( {6 + 2} \right) = 8V\)

Chọn đáp án C

Điện trở tương đương của mạch ngoài được tính theo công thức

 \({R_N} = {{{R_1}{R_2}} \over {{R_1} + {R_2}}} = {{20.30} \over {20 + 30}} = 12\Omega \)

Cường độ dòng điện trong mạch:

 \(I = {E \over {{R_N} + r}} = {{15} \over {12 + 0,5}} = 1,2A\)

Công suất của mạch ngoài

 \({P_N} = {I^2}{R_N} = 1,{2^2}.12 = 17,28W\)

Chọn đáp án C

Vì \(f = {1 \over {2\pi }}\sqrt {{g \over l}} \) nên  \({{{f_1}} \over {{f_2}}} = \sqrt {{{{l_2}} \over {{l_1}}}} \)

Chọn đáp án A

Vì quá trình đẳng nhiệt nên ta có

 \({p_1}{V_1} = {p_2}{V_2} \Rightarrow {p_1}{V_1} = \left( {{p_1} + 6} \right){V_2} \Leftrightarrow 10{p_1} = \left( {{p_1} + 6} \right).4 \Rightarrow {p_1} = 4\left( {at} \right)\)

Chọn đáp án C

Thời gian rơi của vật: \(t=\sqrt{\frac{2h}{g}}=\sqrt{\frac{2.45}{10}}=3s\)

Quãng đường vật đi được trong 2s cuối cùng:

 \(\Delta s=h-\frac{1}{2}g{{\left( t-2 \right)}^{2}}=45-\frac{1}{2}.10.{{\left( 3-2 \right)}^{2}}=45-5=40m\)

Chọn D.

Vì hai dao động cùng pha nên biên độ dao động tổng hợp được tính theo công thức A = A₁ + A₂

Chọn đáp án A

Lực Lo-ren-xơ được tính theo công thức

 \(f = \left| q \right|vB\sin \alpha  = {10.10^{ - 6}}{.10^5}.1.\sin {90^0} = 1N\)

Chọn đáp án A

λ = v/f = 8 cm

* Ta có CN =9 cm= λ + λ /8 ; ND = 32/3 cm = λ + λ /3

+ C cách 1 nút là λ /8 => biên độ dao động tại C là : \({A_C} = {\rm{ }}2a|sin{{2\pi d} \over \lambda }| = {\rm{ }}2a\left| {sin{{2\pi {\lambda  \over 8}} \over \lambda }} \right| = {\rm{ a}}\sqrt 2 \)

+ D cách 1 nút là λ/3 => biên độ dao động tại D là :\({A_D} = {\rm{ }}2a|sin{{2\pi d} \over \lambda }| = {\rm{ }}2a\left| {sin{{2\pi {\lambda  \over 3}} \over \lambda }} \right| = {\rm{ a}}\sqrt 3 \)

* Các phần tử trên cùng 1 bó sóng luôn dao động cùng pha, 2 bó sóng cạnh nhau luôn dao động ngược pha. Từ hình vẽ suy ra u­_C và u_D dao động ngược pha. Ta có

 \({u_C} = a\sqrt 2 \cos \omega t;{u_D} =  - a\sqrt 3 \cos \omega t \Rightarrow {{{u_C}} \over {{u_D}}} =  - {{\sqrt 2 } \over {\sqrt 3 }} \Rightarrow {u_D} =  - {u_C}{{\sqrt 3 } \over {\sqrt 2 }}\)

* Ta có Δt = t₂ – t₁ = 9/40 s = 2T + T/2

 Ở thời điểm t₁ : \({u_C} =  - \sqrt 2 cm\)  => ở thời điểm t₂ :  \({u_C} = \sqrt 2 cm\)

=> Ở thời điểm t₂ : \({u_D} = {u_C}{{ - \sqrt 3 } \over {\sqrt 2 }} = - \sqrt 3 cm\)

Chọn D

Δt là khoảng thời gian giữa hai lần liên tiếp vật có động năng bằng thế năng => Δt = T/4

Theo đề bài ta có  \(v_1^2 + v_2^2 = v_{\max }^2 = {\omega ^2}{A^2}\)

Công thức độc lập với thời gian giữa gia tốc và vận tốc

 \(v_1^2 + {{a_1^2} \over {{\omega ^2}}} = {\omega ^2}{A^2} \Leftrightarrow v_1^2 + {{a_1^2} \over {{\omega ^2}}} = v_1^2 + v_2^2 \Leftrightarrow {{a_1^2} \over {{\omega ^2}}} = v_2^2 \Rightarrow \omega  = {{{a_1}} \over {{v_2}}} = {{2250} \over {45\pi }} = 5\pi \left( {rad/s} \right)\)

Thay vào công thức tính được biên độ dao động  \(A = 6\sqrt 3 cm\)

Chọn đáp án A

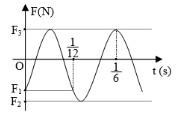
Từ đồ thị ta thấy:

Lực đàn hồi tại thời điểm ban đầu: F = F₁ = - k(Δl₀ + x)

Lực đàn hồi tại vị trí biên dương:  F = F₂= - k(Δl₀ + A)

Lực đàn hồi tại vị trí biên âm: F = F₃ = - k(Δl₀ – A)

Gọi Δt là thời gian từ t = 0 đến t = 1/12s

Ta có: T + Δt/2 = 2Δt => Δt = 2T/3 => x = A/2

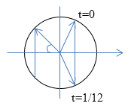
Theo đề bài F₁+2F₂+7F₃=0 => k(Δl₀ + x) +2 k(Δl₀ + A) + 7k(Δl₀ – A) = 0 => Δl₀ = 0,45A

=> Thời gian lo xo nén là t_n = 0,351T

=> Thời gian lò xo giãn là t_g = 0.649T

Do đó tỉ số là 1,849

Chọn đáp án B

Bước sóng λ = v/f = 30/20 = 1,5 cm

Số điểm dao động với biên độ cực đại trên đoạn BM là số giá trị nguyên của k thỏa mãn

 \( - AB \le \left( {k + {1 \over 2}} \right)\lambda  \le MB - MA\)

 \( \Leftrightarrow  - 20 \le \left( {k + {1 \over 2}} \right).1,5 \le 20\sqrt 2  - 20\)

 \( \Leftrightarrow  - 13,8 \le k \le 5,02\)

Có 19 điểm

Chọn đáp án A

Quỹ đạo dài 8 cm => A = 4 cm

Tần số f = 10Hz => ω = 2πf = 20π rad/s

Tại t = 0 vật đi qua vị trí x = - 2cm theo chiều âm => φ = 2π/3 rad

Như vậy, PT dao động của vật là x = 4cos(20pt + 2p/3) cm.

Chọn đáp án D

Vì con ℓắc dao động điều hoà trong điện trường đều mà vectơ cường độ điện trường có độ ℓớn E = 10⁴V/m và hướng thẳng đứng xuống dưới nên

 \(g' = g + a = g + {{\left| q \right|E} \over m} = 10 + {{\left| {{{5.10}^{ - 6}}} \right|{{.10}^4}} \over {0,01}} = 15m/{s^2}\)

Chu kì dao động mới của con lắc đơn

 \(T' = 2\pi \sqrt {{l \over {g'}}}  = 2\pi \sqrt {{{0,5} \over {15}}}  = 1,15s\)

Chọn đáp án C

Công thức của định luật Fa-ra-đây tính khối lượng chất tạo thành ở điện cực là \(m = {1 \over F}.{A \over n}.It\) 

Do  đó ta có  \({{{m_2}} \over {{m_1}}} = {{{t_2}} \over {{t_1}}} = 3 \Rightarrow {m_2} = 3{m_1} = 12g\)

Chọn đáp án B

Mạch RLC xảy ra cộng hưởng nghĩa là Z_L = Z_C → Z = R

Do đó, cường độ dòng điện hiệu dụng được tính theo công thức

 \({U \over R}\)

Chọn đáp án C

Đáp án A

B, C , D – đúng

A – sai

Vì: Một khung dây dẫn hình chữ nhật, quay đều trong một từ trường đều quanh một trục đối xứng OO’ song song với các đường cảm ứng từ thì từ thông trong qua khung không biến thiên, trong khung không xuất hiện dòng điện cảm ứng

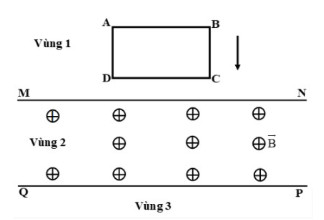
Đáp án: D

Khi khung dây dẫn đang chuyển động giữa vùng 1 và vùng 2, từ thông qua mặt phẳng khung dây tăng, lúc này dòng điện cảm ứng trong khung có chiều ADCBA

Khi khung dây dẫn đang chuyển động giữa vùng 2 và vùng 3, từ thông qua mặt phẳng khung dây giảm, lúc này dòng điện cảm ứng trong khung dây có chiều ABCDA

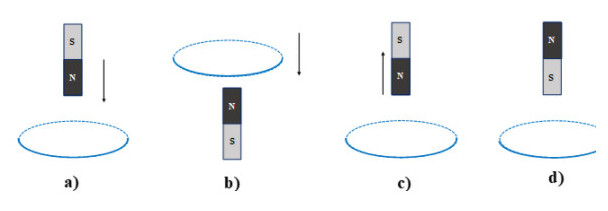
Đáp án: D

Áp dụng định định luật Len – xơ dùng để xác định chiều của dòng điện cảm ứng:

Dòng điện cảm ứng có chiều sao cho nó có tác dụng chống lại nguyên nhân đã sinh ra nó.

Sau đó sử dụng quay tắc nắm bàn tay phải ta xác định được chiều của dòng điện cảm ứng.