Đề thi thử tốt nghiệp THPT QG 2020 môn Vật lý - Trường THPT Thoại Ngọc Hầu
Đề thi thử tốt nghiệp THPT QG 2020 môn Vật lý
-
Hocon247
-
40 câu hỏi
-
90 phút
-
44 lượt thi
-
Trung bình
Tham gia [ Hs Hocon247.com ] - Cộng Đồng Luyện Thi Trực Tuyến để được học tập những kiến thức bổ ích từ HocOn247.com
Một con lắc lò xo gồm lò xo nhẹ và vật nhỏ khối lượng 100g đang dao động điều hòa theo phương ngang, mốc tính thế năng tại vị trí cân bằng. Từ thời điểm t1 = 0 đến \({t_2} = \frac{\pi }{{48}}s\), động năng của con lắc tăng từ 0,096J đến giá trị cực đại rồi giảm về 0,064J. Ở thời điểm t2, thế năng của con lắc bằng 0,064J. Biên độ dao động của con lắc là
Tại thời điểm t1 = 0:
\(\begin{array}{l} {{\rm{W}}_d} = 0,096J;{{\rm{W}}_t} = {\rm{W}} - {{\rm{W}}_d} = 0,032\\ \Rightarrow \frac{{{{\rm{W}}_d}}}{{{{\rm{W}}_t}}} = \frac{{{A^2} - {x^2}}}{{{x^2}}} = 3\\ \Rightarrow x = \pm \frac{A}{2} \end{array}\)
Tại thời điểm t2:
\(\begin{array}{l} {{\rm{W}}_d} = {{\rm{W}}_t}\\ \Rightarrow x = \pm \frac{A}{{\sqrt 2 }}\\ \sin \alpha = \frac{{{x_0}}}{A} = \frac{1}{2} \Rightarrow \alpha = \frac{\pi }{6};\\ \sin \beta = \frac{{\left| {{x_1}} \right|}}{A} = \frac{{\sqrt 2 }}{2} \Rightarrow \beta = \frac{\pi }{4}\\ \Rightarrow \Delta \varphi = \alpha + \beta = \frac{{5\pi }}{{12}}\\ \Delta t = {t_2} - {t_1} = \frac{{\Delta \varphi }}{\omega }\\ \Rightarrow \omega = \frac{{\Delta \varphi }}{{\Delta t}} = 20rad/s\\ \Rightarrow {\rm{W}} = \frac{1}{2}m{\omega ^2}{A^2}\\ \Rightarrow A = \sqrt {\frac{{2W}}{{m{\omega ^2}}}} = 8cm \end{array}\)
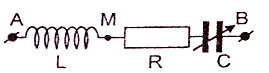
Đặt điện áp xoay chiều ổn định vào hai đầu đoạn mạch AB mắc nối tiếp (hình vẽ). Biết tụ điện có dung kháng ZC, cuộn cảm thuần có cảm kháng ZL và 3ZL = 2ZC. Đồ thị biểu diễn sự phụ thuộc vào thời gian của điện áp giữa hai đầu đoạn mạch AN và điện áp giữa hai đầu đoạn mạch MB như hình vẽ. Điệp áp hiệu dụng giữa hai điểm M và N là
Từ đồ thị:
\(\begin{array}{l} T = {2.10^{ - 2}}s \Rightarrow \omega = \frac{{2\pi }}{T} = 100\pi rad/s;\\ {U_{0AN}} = 200V;{\varphi _{uAN}} = 0;\\ {U_{0MB}} = 100V\\ Khi\,\,t = \frac{2}{3}{.10^{ - 2}}s:\left\{ \begin{array}{l} {\varphi _{t{u_{MB}}}} = \pi \\ {\varphi _{t{u_{AN}}}} = \frac{{2\pi }}{3} \end{array} \right.\\ \Rightarrow {\varphi _{t{u_{MB}}}} - {\varphi _{t{u_{AN}}}} = {\varphi _{{u_{MB}}}} - {\varphi _{{u_{AN}}}} = \frac{\pi }{3}\\ \Rightarrow {\varphi _{{u_{MB}}}} = {\varphi _{{u_{AN}}}} + \frac{\pi }{3} = \frac{\pi }{3} \end{array}\)
Ta có:
\(\begin{array}{l} 3{Z_L} = 2{Z_C} \Rightarrow {U_C} = 1,5{U_L}\\ \left\{ \begin{array}{l} \overrightarrow {{U_{MB}}} = \overrightarrow {{U_L}} + \overrightarrow {{U_X}} \\ \overrightarrow {{U_{AN}}} = \overrightarrow {{U_C}} + \overrightarrow {{U_X}} \end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l} 1,5\overrightarrow {{U_{MB}}} = 1,5\overrightarrow {{U_L}} + 1,5\overrightarrow {{U_X}} \\ \overrightarrow {{U_{AN}}} = \overrightarrow {{U_L}} + \overrightarrow {{U_X}} \end{array} \right.\\ \Rightarrow 2,5\overrightarrow {{U_X}} = 1,5\overrightarrow {{U_{MB}}} + \overrightarrow {{U_{AN}}} \end{array}\)
Dựa vào giản đồ vectơ:
\({U_X} = \frac{{\sqrt {{{\left( {1,5{U_{MB}}} \right)}^2} + U_{AN}^2 + 2.1,5{U_{MB}}.{U_{AN}}\cos \frac{\pi }{3}} }}{{2,5}} = 86V\)
Khi nói về tia hồng ngoại và tia tử ngoại, phát biểu nào sau đây đúng?
Tần số của tia hồng ngoại nhỏ hơn tần số của tia tử ngoại.
Đặt điện áp \(u = 180\sqrt 2 \cos \left( {\omega t} \right)V\) (với \(\omega \) không đổi) vào hai đầu đoạn mạch AB (hình vẽ). R là điện trở thuần, tụ điện có điện dung C, cuộn cảm thuần có độ tự cảm L thay đổi được. Điện áp hiệu dụng ở hai đầu đoạn mạch MB và độ lớn góc lệch pha của cường độ dòng điện so với điện áp u khi L= L1 là U và j1, còn khi L = L2 thì tương ứng là \( \sqrt 8 U\) và j2. Biết \({\varphi _1} + {\varphi _2} = {90^0}\). Giá trị U bằng
Do :
\(\begin{array}{l} {\varphi _1} + {\varphi _2} = \frac{\pi }{2}\\ \Rightarrow x = {Z_{L1}} - {Z_C} = \frac{{{R^2}}}{{{Z_C} - {Z_{{L_2}}}}} = \frac{{{R^2}}}{y}\left( 1 \right)\\ {U_{MB1}} = \frac{{U.\left( {{Z_{L1}} - {Z_C}} \right)}}{{\sqrt {{R^2} + {{\left( {{Z_{L1}} - {Z_C}} \right)}^2}} }} = \frac{{180x}}{{\sqrt {{R^2} + {x^2}} }} = U(2);\\ {U_{MB2}} = \frac{{U.\left( {{Z_C} - {Z_{L2}}} \right)}}{{\sqrt {{R^2} + {{\left( {{Z_C} - {Z_{L2}}} \right)}^2}} }} = \frac{{180y}}{{\sqrt {{R^2} + {y^2}} }} = \sqrt 8 U(3) \end{array}\)
Từ (2) và (3):
\(\frac{x}{y}.\frac{{\sqrt {{R^2} + {y^2}} }}{{\sqrt {{R^2} + {x^2}} }} = \frac{1}{{\sqrt 8 }}\left( 4 \right)\)
Từ (1) và (4):
\(x = \frac{R}{{2\sqrt 2 }}\)
Thay vào (2): U = 60V
Một sóng cơ truyền dọc theo một sợi dây đàn hồi rất dài với biên độ 6mm. Tại một thời điểm, hai phần tử trên dây cùng lệch khỏi vị trí cân bằng 3mm, chuyển động ngược chiều và cách nhau một khoảng ngắn nhất là 8cm (tính theo phương truyền sóng). Gọi d là tỉ số của tốc độ dao động cực đại của một phần tử trên dây với tốc độ truyền sóng. d gần giá trị nào nhất sau đây?
Ta có:
\(\begin{array}{l} \frac{\lambda }{3} = 8cm\\ \Rightarrow \lambda = 24cm\\ \Rightarrow \delta = \frac{{{v_{\max }}}}{v} = \frac{{2\pi fA}}{{\lambda f}} = \frac{{2\pi A}}{\lambda } = 0,157 \end{array}\)
Để ước lượng độ sâu của một giếng cạn nước, một người dùng đồng hồ bấm giây, ghé sát tai vào miệng giếng và thả một hòn đá rơi tự do từ miệng giếng; sau 3s thì người đó nghe thấy tiếng hòn đá đập vào đáy giếng. Giả sử tốc độ truyền âm trong không khí là 330m/s, lấy g = 9,9 m/s2. Độ sâu ước lượng của giếng là
Ta có:
\(\begin{array}{l} 3s = {t_1} + {t_2} = \sqrt {\frac{{2h}}{g}} + \frac{h}{v}\\ \Rightarrow 3 = \sqrt {\frac{{2h}}{{9,9}}} + \frac{h}{{330}} \Rightarrow h \approx 41m \end{array}\)
Một vật nhỏ dao động điều hòa theo một quỹ đạo thẳng dài 14cm với chu kì 1s. Từ thời điểm vật qua vị trí có li độ 3,5cm theo chiều dương đến khi gia tốc của vật đạt giá trị cực tiểu lần thứ hai, vật có tốc độ trung bình là
Ta có:
\(A = \frac{{14}}{2} = 7cm\)
Lần thứ 2 gia tốc của vật đạt gia trị cực tiểu tại M1:
\(\begin{array}{l} \sin \alpha = \frac{x}{A} = \frac{1}{2} \Rightarrow \alpha = \frac{\pi }{6}\\ \Rightarrow \Delta \varphi = 2\pi - \alpha = \frac{{11\pi }}{6}\\ \Rightarrow t = \frac{{\Delta \varphi }}{\omega } = \frac{{11}}{{12}}s \end{array}\)
Quãng đường vật đi đươc:
\(\begin{array}{l} s = \left( {A - {x_0}} \right) + 3A = \left( {7 - 3,5} \right) + 3.7 = 24,5cm\\ \Rightarrow {v_{TB}} = \frac{s}{t} \approx 26,7cm/s \end{array}\)
Một học sinh làm thực hành xác định số vòng dây của hai máy biến áp lí tưởng A và B có các duộn dây với số vòng dây (là số nguyên) lần lượt là N1A, N2A, N1B, N2B. Biết N2A = kN1A; N2B = 2kN1B; k > 1; N1A + N2A + N1B + N2B = 3100 vòng và trong bốn cuộn dây có hai cuộn có số vòng dây đều bằng N. Dùng kết hợp hai máy biến áp này thì có thể tăng điện áp hiệu dụng U thành 18U hoặc 2U. Số vòng dây N là
\(\frac{{{N_{2A}}}}{{{N_{1A}}}} = k;\frac{{{N_{2B}}}}{{{N_{1B}}}} = 2k\)
Có hai khả năng
Trường hợp 1:
\(\begin{array}{l} {N_{2A}} = {N_{1B}} = N\\ \Rightarrow {N_{1B}} = \frac{N}{k};{N_{2B}} = 2kN\\ \Rightarrow {N_{1A}} + {N_{2A}} + {N_{1B}} + {N_{2B}} = 2N + \frac{N}{k} + 2kN = 3100\\ \Rightarrow \left( {2{k^2} + 2k + 1} \right)N = 3100k\\ Khi\,\,{U_{1A}} = U\\ \Rightarrow {U_{2A}} = kU;{U_{1B}} = {U_{2A}} = kU\\ \Rightarrow {U_{2B}} = 2k{U_{1B}} = 2{k^2}U = 18\\ \Rightarrow k = 3\\ \Rightarrow N = 372 \end{array}\)
Nếu : \({U_{2B}} = 2U \Rightarrow k = 1 \Rightarrow N = 620\)
Trường hợp 2:
\(\begin{array}{l} {N_{1A}} = {N_{2B}} = N\\ \Rightarrow {N_{1B}} = \frac{N}{{2k}};{N_{2A}} = kN\\ \Rightarrow {N_{1A}} + {N_{2A}} + {N_{1B}} + {N_{2B}} = 2N + \frac{N}{{2k}} + kN = 3100\\ \Rightarrow \left( {2{k^2} + 4k + 1} \right)N = 6200k\\ \Rightarrow {U_{2B}} = 2k{U_{1B}} = 2{k^2}U = 18U\\ \Rightarrow k = 3\\ \Rightarrow N = 600 \end{array}\)
Trong một thí nghiệm giao thoa sóng nước, hai nguồn A và B cách nhau 16cm, dao động theo phương vuông góc với mặt nước, cùng biên độ, cùng pha, cùng tần số 80Hz. Tốc độ truyền sóng trên mặt nước là 40cm/s. Ở mặt nước, gọi d là đường trung trực của đoạn AB. Trên d, điểm M ở cách A 10cm; điểm N dao động cùng pha với M và gần M nhất sẽ cách M một đoạn có giá trị gần giá trị nào nhất sau đây?
Ta có:
\(\lambda = \frac{v}{f} = 0,5cm.\)
Độ lệch pha của 2 điểm M, N trên đường trung trực của AB:
\(\Delta \varphi = 2\pi \frac{{{d_2} - {d_1}}}{\lambda }\)
N dao động cùng pha với M khi:
\(\begin{array}{l} \Delta \varphi = 2k\pi \Rightarrow {d_2} - {d_1} = k\lambda \\ \Rightarrow {d_2} = {d_1} + k\lambda \end{array}\)
Điểm gần nhất dao động cùng pha với M ứng với k = 1
\(\Rightarrow {d_2} = {d_1} + \lambda = 10 + 0,5 = 10,5cm\)
Ta có:
\(\begin{array}{l} NH = \sqrt {d_2^2 - A{H^2}} ;MH = \sqrt {d_1^2 - A{H^2}} \\ \Rightarrow NM = \left| {\sqrt {d_2^2 - A{H^2}} - \sqrt {d_1^2 - A{H^2}} } \right| = 8mm \end{array}\)
Theo mẫu Bo về nguyên tử hiđrô, nếu lực tương tác tĩnh điện giữa êlectron và hạt nhân khi êlectron chuyển động trên quỹ đạo dừng L là F thì khi êlectron chuyển động trên quỹ đạo dừng N, lực này sẽ là
Lực tương tác tĩnh điện giữa electron và hạt nhân:
\(F = k\frac{{{e^2}}}{{{r^2}}} \Rightarrow \frac{{{F_N}}}{{{F_L}}} = \frac{{r_L^2}}{{r_N^2}} = {\left( {\frac{{4{r_0}}}{{16{r_0}}}} \right)^2} = \frac{1}{{16}}\)
Trong môi trường đẳng hướng và không hấp thụ âm, có 3 điểm thẳng hàng theo đúng thứ tự A; B; C với AB = 100m, AC = 250m. Khi đặt tại A một nguồn điểm phát âm công suất P thì mức cường độ âm tại B là 100 dB. Bỏ nguồn âm tại A, đặt tại B một nguồn điểm phát âm công suất 2P thì mức cường độ âm tại A và C là
Khi nguồn đặt tại A:
\(\begin{array}{l} {L_B} = 10\lg \frac{{{I_B}}}{{{I_0}}} = 10\lg \left( {\frac{P}{{{I_0}4\pi R_B^2}}} \right)\\ \Rightarrow \frac{P}{{{I_0}4\pi R_B^2}} = {10^{10}} \end{array}\)
Khi nguồn âm đặt tại B:
\(\begin{array}{l} {L_A} = 10\lg \frac{{{I_A}}}{{{I_0}}} = 10\lg \left( {\frac{{2P}}{{{I_0}4\pi R_A^2}}} \right) = 10\lg \left( {{{2.10}^{10}}} \right) = 103dB\\ {L_B} = 10\lg \left( {\frac{{2P}}{{{I_0}4\pi R_B^{,2}}}} \right) = 10\lg \left( {\frac{{2P}}{{{I_0}4\pi .1,{5^2}R_A^2}}} \right) = 10\lg \left( {\frac{{{{2.10}^{10}}}}{{1,{5^2}}}} \right) = 99,5dB \end{array}\)
Một vật có khối lượng 50g, dao động điều hòa với biên độ 4 cm và tần số góc 3rad/s. Động năng cực đại của vật là
Động năng cực đại của vật bằn cơ năng của vật:
\(W = \frac{1}{2}m{\omega ^2}{A^2} = 3,{6.10^{ - 4}}J\)
Trong chân không, một ánh sáng có bước sóng là 0,60mm. Năng lượng của phôtôn ánh sáng này bằng
Năng lượng của photon:
\(\varepsilon = \frac{{hc}}{\lambda } = 2,07eV\)
Các thao tác cơ bản khi sử dụng đồng hồ đa năng hiện số (hình vẽ) để đo điện áp xoay chiều cỡ 120 V gồm:
a. Nhấn nút ON OFF để bật nguồn của đồng hồ.
b. Cho hai đầu đo của hai dây đo tiếp xúc với hai đầu đoạn mạch cần đo điện áp.
c. Vặn đầu đánh dấu của núm xoay tới chấm có ghi 200, trong vùng ACV.
d. Cắm hai đầu nối của hai dây đo vào hai ổ COM và VW.
e. Chờ cho các chữ số ổn định, đọc trị số của điện áp.
g. Kết thúc các thao tác đo, nhấn nút ON OFF để tắt nguồn của đồng hồ.
Thứ tự đúng các thao tác là
Thứ tự đúng các thao tác là c, d, a, b, e, g.
Vặn đầu đánh dấu của núm xoay tới chấm có ghi 200, trong vùng ACV.
Cắm hai đầu nối của hai dây đo vào hai ổ COM và VW.
Nhấn nút ON OFF để bật nguồn của đồng hồ.
Cho hai đầu đo của hai dây đo tiếp xúc với hai đầu đoạn mạch cần đo điện áp.
Chờ cho các chữ số ổn định, đọc trị số của điện áp.
Kết thúc các thao tác đo, nhấn nút ON OFF để tắt nguồn của đồng hồ.
Một động cơ điện tiêu thụ công suất điện 110W, sinh ra công suất cơ học bằng 88W. Tỉ số của công suất cơ học với công suất hao phí ở động cơ bằng
Ta có:
\(\frac{{{P_1}}}{{{P_2}}} = \frac{{{P_1}}}{{P - {P_1}}} = \frac{{88}}{{110 - 88}} = 4\)
Một vật dao động cưỡng bức dưới tác dụng của một ngoại lực biến thiên điều hòa với tần số f. Chu kì dao động của vật là
Chu kì của dao động cưỡng bức bằng chu kì của ngoại lực cưỡng bức.
Do đó: \(T= \frac{1}{{ f}}\)
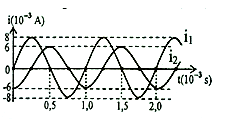
Hai mạch dao động điện từ LC lí tưởng đang có dao động điện từ tự do với các cường độ dòng điện tức thời trong hai mạch là i1 và i2 được biểu diễn như hình vẽ. Tổng điện tích của hai tụ điện trong hai mạch ở cùng một thời điểm có giá trị lớn nhất bằng
Từ đồ thị:
\(T = {10^{ - 3}}s \Rightarrow \omega = \frac{{2\pi }}{T} = 2000\pi rad/s\)
Khi t = 0:
Đối với i1:
\(\begin{array}{l} \left\{ \begin{array}{l} {i_1} = 0\\ i_1^, > 0 \end{array} \right. \Rightarrow {\varphi _{i1}} = - \frac{\pi }{2};{I_{01}} = {8.10^{ - 3}}A\\ \Rightarrow {i_1} = {8.10^{ - 3}}\cos \left( {200\pi t - \frac{\pi }{2}} \right)A \end{array}\)
Đối với i2:
\(\begin{array}{l} \left\{ \begin{array}{l} {i_2} = - {6.10^{ - 3}}A\\ i_1^, = 0 \end{array} \right. \Rightarrow {\varphi _{i1}} = \pi ;{I_{01}} = {6.10^{ - 3}}A\\ \Rightarrow {i_1} = {6.10^{ - 3}}\cos \left( {200\pi t + \pi } \right)A \end{array}\)
Do đó biểu thức điện tích tương ứng:
\(\left\{ \begin{array}{l} {i_1} = q_1^, \Rightarrow {q_1} = \frac{{{{8.10}^{ - 3}}}}{{2000\pi }}\cos \left( {2000\pi - \pi } \right)\\ {i_2} = q_2^, \Rightarrow {q_2} = \frac{{{{6.10}^{ - 3}}}}{{2000\pi }}\cos \left( {2000\pi + \frac{\pi }{2}} \right) \end{array} \right.\)
Ta có:
\(\begin{array}{l} q = {q_1} + {q_2}\\ \Delta \varphi = {\varphi _{q2}} - {\varphi _{q1}} = \frac{{3\pi }}{2}\\ \Rightarrow {q_{\max }} = {\left( {{q_1} + {q_2}} \right)_{\max }} = \sqrt {Q_{01}^2 + Q_{02}^2} = \frac{{{{10.10}^{ - 3}}}}{{2000\pi }} = \frac{5}{\pi }\mu C \end{array}\)
Bắn hạt α vào hạt nhân nguyên tử nhôm đang đứng yên gây ra phản ứng: \({}_2^4He + {}_{13}^{27}Al \to {}_{15}^{30}P + {}_0^1n\). Biết phản ứng thu năng lượng là 2,70MeV; giả sử hai hạt tạo thành bay ra với cùng vận tốc và phản ứng không kèm bức xạ γ. Lấy khối lượng của các hạt tính theo đơn vị u có giá trị bằng số khối của chúng. Động năng của hạt α là
Áp dụng định luật bảo toàn động lượng ta có:
\(\begin{array}{l} {p_\alpha } = {p_n} + {p_p}\\ \Rightarrow {m_\alpha }{K_\alpha } = {m_n}{K_n} + {m_p}{K_p} + 4\sqrt {{m_n}{K_n}.{m_p}{K_p}} \\ \Leftrightarrow 4{K_\alpha } = {K_n} + 30{K_p} + 4\sqrt {30{K_n}.{K_p}} \left( 1 \right) \end{array}\)
Áp dụng định luật bảo toàn năng lượng:
\({K_\alpha } = 2,7 + {K_n} + {K_p}\left( 2 \right)\)
Mặt khác:
\(\frac{{{K_n}}}{{{K_p}}} = \frac{{{m_n}}}{{{m_p}}} = \frac{1}{{30}}\left( 3 \right)\)
Từ (1); (2) và (3): \(\Rightarrow {K_\alpha } = 3,1MeV\)
Trong phản ứng hạt nhân không có sự bảo toàn
Trong phản ứng hạt nhân không có sự bảo toàn số nơtron.
Trong chân không, các bức xạ có bước sóng tăng dần theo thứ tự đúng là
Trong chân không, các bức xạ có bước sóng tăng dần theo thứ tự đúng là :
Tia gamma; tia X; tia tử ngoại; ánh sáng nhìn thấy; tia hồng ngoại và sóng vô tuyến.
Trong chân không, bước sóng ánh sáng lục bằng
Trong chân không, bước sóng ánh sáng lục bằng 546nm.
Một con lắc lò xo treo vào một điểm cố định, dao động điều hòa theo phương thẳng đứng với chu kì 1,2s. Trong một chu kì, nếu tỉ số của thời gian lò xo giãn với thời gian lò xo nén bằng 2 thì thời gian mà lực đàn hồi ngược chiều lực kéo về là
Chọn chiều dương hướng lên, gốc tọa độ tại vị trí cân bằng
Gọi \(\Delta {\varphi _1};\Delta {\varphi _2}\) là góc quét ứng vời thời gian lò xo nén và dãn:
\(\begin{array}{l} \frac{{\Delta {\varphi _2}}}{{\Delta {\varphi _1}}} = \frac{{2\pi - \Delta {\varphi _1}}}{{\Delta {\varphi _1}}} = \frac{{{t_2}}}{{{t_1}}} = 2\\ \Rightarrow \Delta {\varphi _1} = \frac{{2\pi }}{3}\\ \Rightarrow \alpha = \frac{{\Delta \varphi }}{2} = \frac{\pi }{3}\\ \Rightarrow \beta = \frac{\pi }{2} - \alpha = \frac{\pi }{6} \end{array}\)
Lực đàn hồi ngược chiều với lực kéo khi lò xo bị dãn và \(0 \le x \le \frac{A}{2}\)
Góc quét ứng với thời gian lực đàn hồi ngược chiều lực hồi phục
\(\Delta {\varphi _1} = 2\beta = \frac{\pi }{3} \Rightarrow {t_1} = \frac{{\Delta {\varphi _1}}}{{\frac{{2\pi }}{T}}} = \frac{T}{6} = 0,2s\)
Trong thí nghiệm Young về giao thoa ánh sáng, khoảng cách giữa hai khe là 1mm, khoảng cách từ mặt phẳng chứa hai khe đến màn quan sát là 2m. Nguồn sáng đơn sắc có bước sóng \(0,45\mu m\). Khoảng vân giao thoa trên màn bằng
Khoảng vân:
\(i = \frac{{\lambda D}}{a} = 0,9mm\)
Đặt điện áp \(u = {U_0}\cos \left( {100\pi t + \frac{\pi }{4}} \right)V\) vào hai đầu đoạn mạch chỉ có tụ điện thì cường độ dòng điện trong mạch là \(i = {I_0}\cos \left( {100\pi t + \varphi } \right)A\). Giá trị của φ bằng
Đối với mạch chỉ có tụ điện ta có:
\({\varphi _u} - {\varphi _i} = - \frac{\pi }{2} \Rightarrow {\varphi _i} = {\varphi _u} + \frac{\pi }{2} = \frac{{3\pi }}{4}\)
Gọi nđ, nt và nv lần lượt là chiết suất của một môi trường trong suốt đối với các ánh sáng đơn sắc đỏ, tím và vàng. Sắp xếp nào sau đây là đúng?
Chiết suất của một môi trường tằng theo tần số của sóng ánh sáng. Do đó: nđ< nv< nt.
Một đoạn mạch điện xoay chiều gồm điện trở thuần R mắc nối tiếp với một cuộn cảm thuần có cảm kháng với giá trị bằng R. Độ lệch pha của điện áp giữa hai đầu đoạn mạch với cường độ dòng điện trong mạch bằng
Ta có:
\(\begin{array}{l} \tan \varphi = \frac{{{Z_L}}}{R} = 1\\ \Rightarrow \varphi = \frac{\pi }{4} \Rightarrow {\varphi _u} - {\varphi _i} = \varphi = \frac{\pi }{4} \end{array}\)
Hiện tượng chùm ánh sáng trắng đi qua lăng kính, bị phân tách thành các chùm sáng đơn sắc là hiện tượng
Hiện tượng chùm ánh sáng trắng đi qua lăng kính, bị phân tách thành các chùm sáng đơn sắc là hiện tượng tán sắc ánh sáng.
Chùm ánh sáng laze không được ứng dụng
Chùm ánh sáng laze không được ứng dụng làm nguồn phát siêu âm.
Tia α
Tia α là dòng các hạt nhân \({}_{\rm{2}}^{\rm{4}}{\rm{He}}\).
Đặt điện áp \(u = U\sqrt 2 \cos \left( {\omega t} \right)V\) vào hai đầu đoạn mạch mắc nối tiếp gồm đèn sợi đốt có ghi 220V – 100W, cuộn cảm thuần có độ tự cảm L và tụ điện có điện dung C. Khi đó đèn sáng đúng công suất định mức. Nếu nối tắt hai bản tụ điện thì đèn chỉ sáng với công suất bằng 50W. Trong hai trường hợp, coi điện trở của đèn như nhau, bỏ qua độ tự cảm của đèn. Dung kháng của tụ điện không thể là giá trị nào trong các giá trị sau?
Điện trở của bóng đèn: \(R = \frac{{U_{dm}^2}}{{{P_{dm}}}} = 484\Omega \)
Lúc đầu đèn sáng bình thường:
\(P = R{I^2} = 100W\)
Khi nối tắt tụ C: \({P^,} = R{I^{,2}} = 50W\)
Ta có:
\(\begin{array}{l} \frac{{{I^,}}}{I} = \frac{Z}{{{Z^2}}} = \frac{{\sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }}{{\sqrt {{R^2} + Z_L^2} }}\frac{1}{{\sqrt 2 }}\\ \Leftrightarrow Z_L^2 - 4{Z_C}{Z_L} + {R^2} + 2Z_C^2 = 0 \end{array}\)
Điều kiện để phương trình có nghiệm:
\(\begin{array}{l} {\Delta ^,} = 4Z_C^2 - {R^2} - 2Z_C^2 \ge 0\\ \Rightarrow {Z_C} \ge \frac{R}{{\sqrt 2 }} = 342\Omega \end{array}\)
Vậy ZL không thể có giá trị 274Ω
Một tụ điện có điện dung C tích điện Q0. Nếu nối tụ điện với cuộn cảm thuần có độ tự cảm L1 hoặc với cuộn cảm thuần có độ tự cảm L2 thì trong mạch có dao động điện từ tự do với cường độ dòng điện cực đại là 20mA hoặc 10mA. Nếu nối tụ điện với cuộn cảm thuần có độ tự cảm \({L_3} = 9{L_1} + 4{L_2}\) thì trong mạch có dao động điện từ tự do với cường độ dòng điện cực đại là
Ta có:
\(\begin{array}{l} {Q_0} = \frac{{{I_{01}}}}{{{\omega _1}}} = \frac{{{I_{02}}}}{{{\omega _2}}}\\ \Rightarrow \frac{{{\omega _1}}}{{{\omega _2}}} = \frac{{{I_{01}}}}{{{I_{02}}}} = \sqrt {\frac{{{L_2}C}}{{{L_1}C}}} = \sqrt {\frac{{{L_2}}}{{{L_1}}}} = 2\\ \Rightarrow {L_2} = 4{L_1} \end{array}\)
Theo giả thiết: \({L_3} = 9{L_1} + 4{L_2} = 25{L_1}\)
Tương tự:
\(\begin{array}{l} \frac{{{\omega _1}}}{{{\omega _3}}} = \frac{{{I_{01}}}}{{{I_{03}}}} = \sqrt {\frac{{{L_3}}}{{{L_1}}}} = 5\\ \Rightarrow {I_{03}} = \frac{{{I_{01}}}}{5} = 4mA \end{array}\)
Trong các hạt nhân nguyên tử: \({}_2^4He;{}_{26}^{56}Fe;{}_{92}^{238}U;{}_{90}^{230}Th\), hạt nhân bền vững nhất là
Hạt nhân bền vững nhất là \( {}_{26}^{56}Fe \)
Trên một sợi dây đàn hồi đang có sóng dừng ổn định với khoảng cách giữa hai nút sóng liên tiếp là 6cm. Trên dây có những phần tử sóng dao động với tần số 5Hz và biên độ lớn nhất là 3cm. Gọi N là vị trí của một nút sóng; C và D là hai phần tử trên dây ở hai bên của N và có vị trí cân bằng cách N lần lượt là 10,5cm và 7cm. Tại thời điểm t1, phần tử C có li độ 1,5cm và đang hướng về vị trí cân bằng. Vào thời điểm \({t_2} = {t_{\kern 1pt} }_1 + \frac{{79}}{{40}}s\), phần tử D có li độ là
Ta có khoảng cách giữa hai nút sóng liên tiêp:
\(\frac{\lambda }{2} = 6cm \Rightarrow \lambda = 12cm\)
Biên độ của nguồn sóng xác định bởi:
\(2a = 3cm \Rightarrow a = 1,5cm\)
Phương trình sóng dừng cách nút N một đoạn d:
\(u = 2a\cos \left( {2\pi \frac{d}{\pi } + \frac{\pi }{2}} \right)\cos \left( {\omega t - \frac{\pi }{2}} \right)\)
Do đó:
\(\begin{array}{l} {a_C} = 2a\left| {\cos \left( {2\pi \frac{{{d_C}}}{\lambda } + \frac{\pi }{2}} \right)} \right| = 1,5\sqrt 2 cm;\\ {a_D} = 2a\left| {\cos \left( {2\pi \frac{{{d_D}}}{\lambda } + \frac{\pi }{2}} \right)} \right| = 1,5cm \end{array}\)
Độ lệch pha dao động của phần tử C ở thời điểm t1 và thời điểm \({t_1} + \frac{{79}}{{40}}s\) là:
\(\Delta \varphi = 2\pi f.\frac{{79}}{{40}} = 18\pi + 1,75\pi \)
Dựa vào vòng tròn lượng giác:
\(\cos \alpha = \frac{{1,5}}{{1,5\sqrt 2 }} = \frac{{\sqrt 2 }}{2} \Rightarrow \alpha = \frac{\pi }{4}\)
Vậy tại thời điểm t2 điểm C ở vị trí biên dương C2
Vì C và D nằm ở hai bên bó sóng liền kề nên chúng luôn dao động ngược pha.
Do đó, khi C ở biên dương thì D đang ở biên âm. Vậy li độ của D là \({x_D} = - {a_D} = - 1,5cm\)
Một mạch dao động LC lí tưởng đang có dao động điện từ tự do với điện tích cực đại của tụ điện là Q0 và cường độ dòng điện cực đại trong mạch là I0. Dao động điện từ tự do trong mạch có chu kì là
\(\begin{array}{l} \frac{{Q_0^2}}{{2C}} = \frac{{LI_0^2}}{2} \Rightarrow LC = \frac{{Q_0^2}}{{I_0^2}}\\ \Rightarrow T = 2\pi \sqrt {LC} = 2\pi .\frac{{{Q_0}}}{{{I_0}}} \end{array}\)
Một con lắc lò xo dao động điều hòa theo phương ngang với tần số góc ω. Vật nhỏ của con lắc có khối lượng 100g. Tại thời điểm t = 0, vật nhỏ qua vị trí cân bằng theo chiều dương. Tại thời điểm t = 0,95s, vận tốc v và li độ x của vật nhỏ thỏa mãn v= - ωx lần thứ 5. Độ cứng của lò xo là
Ta có phương trình dao động của vật là:
\(x = A\cos \left( {\omega t - \frac{\pi }{2}} \right)\)
Vận tốc v= - ωx ứng với trường hợp vật hướng về vị trí cân bằng
Khi t = 0,95s:
\(\begin{array}{l} v = \pm \omega \sqrt {{A^2} - {x^2}} = - \omega x\\ \Rightarrow x = \pm \frac{A}{{\sqrt 2 }} \end{array}\)
Thời điểm đầu tiên vật qua v= - ωxở M1:
\(\begin{array}{l} \cos \alpha = \frac{{\frac{A}{{\sqrt 2 }}}}{A} = \frac{{\sqrt 2 }}{2}\\ \Rightarrow \alpha = \frac{\pi }{4}\\ \Rightarrow \Delta \varphi = \frac{\pi }{2} + \alpha = \frac{{3\pi }}{4}\\ \Rightarrow {t_1} = \frac{{\Delta \varphi }}{{\frac{{2\pi }}{T}}} = \frac{{3T}}{8} \end{array}\)
Mỗi chu kì vật qua v= - ωx hai lần, do đó lần thứ 5:
\(\begin{array}{l} t = {t_1} + 2T = \frac{{19T}}{8}\\ \Rightarrow T = \frac{{8t}}{{19}} = 0,4s\\ \Rightarrow k = \frac{{4{\pi ^2}m}}{{{T^2}}} = 25N/m \end{array}\)
Một con lắc đơn dao động điều hòa với biên độ góc 0,1rad; tần số góc 10rad/s và pha ban đầu 0,79rad. Phương trình dao động của con lắc là
Phương trình dao động của con lắc là:
\(\alpha = 0,1\cos \left( {10t + 0,79} \right)rad\)
Đồng vị là những nguyên tử mà hạt nhân có cùng số
Đồng vị là những nguyên tử mà hạt nhân có cùng số prôtôn nhưng khác số nuclôn
Trong âm nhạc, khoảng cách giữa hai nốt nhạc trong một quãng được tính bằng cung và nửa cung (nc). Mỗi quãng tám được chia thành 12 nc. Hai nốt nhạc cách nhau nửa cung thì hai âm (cao, thấp) tương ứng với hai nốt nhạc này có tần số thỏa mãn \(f_c^{12} = 2f_t^{12}\). Tập hợp tất cả các âm trong một quãng tám gọi là một gam (âm giai). Xét một gam với khoảng cách từ nốt Đồ đến các nốt tiếp theo Rê, Mi, Fa, Sol, La, Si, Đô tương ứng là 2 nc, 4 nc, 5 nc, 7 nc , 9 nc, 11 nc, 12 nc. Trong gam này, nếu âm ứng với nốt La có tần số 440 Hz thì âm ứng với nốt Sol có tần số là
Khoảng cách từ nốt sol đến nốt là 2nc nên ta có:
\(\begin{array}{l} f_L^{12} = 2.\left( {2f_S^{12}} \right) = 4f_S^{12}\\ \Rightarrow {f_S} = {f_L}\sqrt[{12}]{4} = 440.\sqrt[{12}]{4} \approx 392Hz \end{array}\)
Đặt điện áp xoay chiều có giá trị hiệu dụng 200V và tần số không thay đổi vào hai đầu đoạn mạch AB (hình vẽ). Cuộn cảm thuần có độ tự cảm L xác định; R = 200Ω; tụ điện có điện dung C thay đổi được. Điều chỉnh điện dung C để điện áp hiệu dụng giữa hai đầu đoạn mạch MB đạt giá trị cực tiểu là U1 và giá trị cực đại là U2 = 400V. Giá trị của U1 là
Ta có:
UMB = \(\frac{{U\sqrt {{R^2} + Z_C^2} }}{{\sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }} = \frac{U}{{\sqrt {\frac{{{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}}}{{{R^2} + Z_C^2}}} }} = \frac{U}{{\sqrt y }}\)
với \(y = \frac{{{R^2} + {{({Z_L} - {Z_C})}^2}}}{{{R^2} + Z_C^2}}\)
\(\begin{array}{l} {y^,} = \frac{{ - 2\left( {{Z_L} - {Z_C}} \right)\left( {{R^2} + Z_C^2} \right) - 2{Z_C}\left[ {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} \right]}}{{{{\left( {{R^2} + Z_C^2} \right)}^2}}}\\ \Leftrightarrow y' = \frac{{2{Z_L}\left( {Z_C^2 - {Z_L}{Z_C} - {R^2}} \right)}}{{{{\left( {{R^2} + Z_C^2} \right)}^2}}}\\ y' = \,\,khi\,\,\,{Z_C} = \frac{{{Z_L} + \sqrt {4{R^2} + Z_L^2} }}{2} \end{array}\)
Khi đó :
\(\begin{array}{l} {U_{MB\max }} = \frac{{2UR}}{{\sqrt {4{R^2} + Z_L^2} - {Z_L}}} = {U_2}\\ \frac{R}{{\sqrt {4{R^2} + Z_L^2} - {Z_L}}} = 1 \Rightarrow {\left( {R + {Z_L}} \right)^2} = 4{R^2} + Z_L^2\\ \Rightarrow {Z_L} = 1,5R\left( 1 \right) \end{array}\)
UMB = UMBmin khi ZC = 0 vì với ZC > 0 thì:
\(\begin{array}{l} \frac{{\sqrt {{R^2}} }}{{\sqrt {{R^2} + Z_L^2} }} < \frac{{\sqrt {{R^2} + Z_C^2} }}{{\sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }}\\ {U_{MB\min }} = \frac{{U\sqrt {{R^2}} }}{{\sqrt {{R^2} + Z_L^2} }} = \frac{{UR}}{{\sqrt {{R^2} + Z_L^2} }} = {U_1}\\ {U_1} = \frac{{UR}}{{\sqrt {{R^2} + Z_L^2} }} = \frac{{UR}}{{\sqrt {{R^2} + 2,25{R^2}} }} = \frac{U}{{\sqrt {3,25} }}\\ \Leftrightarrow {U_1} = \frac{{200}}{{\sqrt {3,25} }} \approx 111V \end{array}\)
Cho hai dao động điều hòa cùng phương với các phương trình lần lượt là \({x_1} = {A_1}\cos \left( {\omega t + 0,35} \right)cm;{x_2} = {A_2}\cos \left( {\omega t - 1,57} \right)cm\). Dao động tổng hợp của hai dao động này có phương trình là \(x = 20\cos \left( {\omega t + \varphi } \right)cm\). Giá trị cực đại của (A1 + A2) gần giá trị nào nhất sau đây?
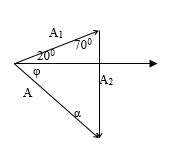
Áp dụng định lý hàm số sin ta có:
\(\begin{array}{l} \frac{{{A_1}}}{{\sin \alpha }} = \frac{{{A_2}}}{{\sin \left( {{{20}^0} - \varphi } \right)}} = \frac{A}{{\sin {{70}^0}}}\\ \Rightarrow {A_1} = \frac{A}{{\sin {{70}^0}}}\sin \alpha = \frac{A}{{0,94}}\cos \varphi ;\\ {A_2} = \frac{A}{{\sin {{70}^0}}}.\sin \left( {{{20}^0} - \varphi } \right) = \frac{A}{{0,94}}.\sin \left( {{{20}^0} - \varphi } \right)\\ \Rightarrow {A_1} + {A_2} = \frac{A}{{0,94}}.\left[ {\cos \varphi + \sin \left( {{{20}^0} - \varphi } \right)} \right]\\ = \frac{A}{{0,94}}.\left[ {\cos \varphi + \cos \left( {{{70}^0} + \varphi } \right)} \right]\\ = \frac{{2A}}{{0,94}}\cos \left( {{{35}^0} + \varphi } \right)\cos {35^0} = 1,64A\cos \left( {{{35}^0} + \varphi } \right)\\ \Rightarrow {\left( {{A_1} + {A_2}} \right)_{\max }} = 1,64A = 32,8cm \end{array}\)

.PNG)
.PNG)
.PNG)


.PNG)