Trắc nghiệm Chuyên đề Khối đa diện ôn thi THPT QG năm 2019 -
Trắc nghiệm Chuyên đề Khối đa diện ôn thi THPT QG năm 2019 -
-
Hocon247
-
40 câu hỏi
-
90 phút
-
42 lượt thi
-
Dễ
Tham gia [ Hs Hocon247.com ] - Cộng Đồng Luyện Thi Trực Tuyến để được học tập những kiến thức bổ ích từ HocOn247.com
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thang với \(AD\,{\rm{//}}\,BC\) và \(AD = 2BC\). Kết luận nào sau đây đúng?
.png)
Ta có \({S_{\Delta ABC}} = \frac{1}{3}{S_{ABCD}} \Rightarrow {V_{S.ABC}} = \frac{1}{3}{V_{S.ABCD}}\)
Cho khối chóp \(S.ABC\) có thể tích \(V\), nếu giữ nguyên chiều cao và tăng các cạnh đáy lên 3 lần thì thể tích khối chóp thu được là:
Gọi \(a, b, c\) lần lượt là độ dài các cạnh của \(\Delta ABC\). Đặt \(p = \frac{{3\left( {a + b + c} \right)}}{2}\)
thì \({S_1} = \sqrt {3.\frac{{a + b + c}}{2}.3\left( {p - a} \right).3\left( {p - b} \right).3\left( {p - c} \right)} = 9{S_{ABC}}\)
\( \Rightarrow \) Thể tích khối chóp thu được là \(9V\).
Một hình hộp chữ nhật \(ABCD.A'B'C'D'\) có ba kích thước là \(2 cm, 3 cm\) và \(6 cm\). Thể tích của khối tứ diện \(ACB'D'\) bằng
.png)
Thể tích khối hộp chữ nhật \(ABCD.A'B'C'D'\) là \(V = 2.3.6 = 36\left( {{{{\mathop{\rm cm}\nolimits} }^3}} \right)\).
Ta có \({V_{A.A'B'D'}} = {V_{C.C'B'D'}} = {V_{D'.DAC}} = {V_{B'.BAC}} = \frac{1}{6}V\).
Nên: \({V_{ACB'D'}} = V - \left( {{V_{A.A'B'D'}} + {V_{C.C'B'D'}} + {V_{D'.DAC}} + {V_{B'.BAC}}} \right) = V - \frac{4}{6}V = \frac{1}{3}V = \frac{1}{3}.36 = 12\left( {{{{\mathop{\rm cm}\nolimits} }^3}} \right)\).
Cho khối chóp \(S.ABC\), gọi \(G\) là trọng tâm của tam giác \(ABC\). Tỉ số thể tích \(\frac{{{V_{S.ABC}}}}{{{V_{S.AGC}}}}\) bằng

Ta có \(\frac{{{V_{S.ABC}}}}{{{V_{S.AGC}}}} = \frac{{{S_{\Delta ABC}}}}{{{S_{\Delta AGC}}}} = \frac{{d\left( {B;AC} \right)}}{{d\left( {G;AC} \right)}} = \frac{{BO}}{{GN}} = \frac{{BL}}{{GL}} = 3\)
Khối bát diện đều có bao nhiêu mặt phẳng đối xứng?
.png)
Hình bát diện \(ABCDEF\) có 9 mặt phẳng đối xứng: 3 mặt phẳng \(\left( {ABCD} \right),\left( {BEDF} \right),\left( {AECF} \right)\) và 6 mặt phẳng mà mỗi mặt phẳng là trung trực của hai cạnh song song.
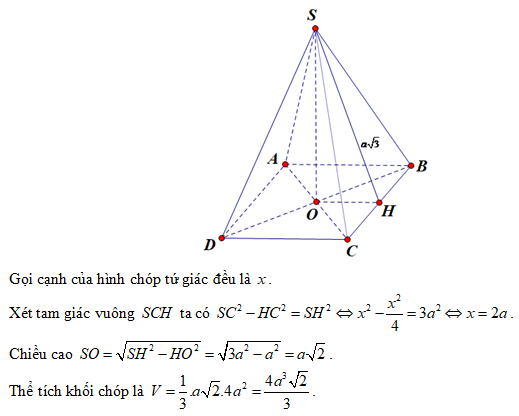
Cho khối chóp \(S.ABCD\) có thể tích bằng \(\sqrt 3 {a^3}\). Mặt bên \(SAB\) là tam giác đều cạnh \(a\) thuộc mặt phẳng vuông góc với đáy, biết đáy \(ABCD\) là hình bình hành. Tính theo \(a\) khoảng cách giữa \(SA\) và \(CD\).
.png)
Gọi \(H\) là trung điểm của \(AB \Rightarrow SH \bot \left( {ABC{\rm{D}}} \right)\) và \(SH = \frac{{a\sqrt 3 }}{2}\).
Kẻ \(CK \bot AB\)
Ta có \({S_{ABCD}} = \frac{{3V}}{{SH}} = \frac{{3\sqrt 3 {a^3}}}{{\frac{{a\sqrt 3 }}{2}}} = 6{a^2}\)
Mặt phẳng \((SAB)\) là mặt phẳng chứa \(SA\) và song song \(CD\). Do đó \(d\left( {SA,CD} \right) = d\left( {C,\left( {SAB} \right)} \right)\)
Ta thấy \(\left\{ \begin{array}{l}
CK \bot AB\\
CK \bot SH
\end{array} \right. \Rightarrow CK \bot \left( {SAB} \right)\).
Do đó \(d\left( {C,\left( {SAB} \right)} \right) = CK = \frac{{{S_{ABCD}}}}{{AB}} = \frac{{6{a^2}}}{a} = 6a.\)
Cho khối chóp \(S.ABCD\) có thể tích \(V\). Các điểm \(A', B', C'\) tương ứng là trung điểm các cạnh \(SA, SB, SC\). Thể tích khối chóp \(S.A'B'C'\) bằng
Ta có \(\frac{{{V_{S.A'B'C'}}}}{{{V_{S.ABC}}}} = \frac{{SA'}}{{SA}} \cdot \frac{{SB'}}{{SB}} \cdot \frac{{SC'}}{{SC}} = \frac{1}{8} \Rightarrow {V_{S.A'B'C'}} = \frac{V}{8}\)

.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
.png)
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
.png)
.PNG)
.PNG)



