Cho hàm số \(y=(x+2)(x-1)^{2}\) có đồ thị như hình vẽ. Hỏi mệnh đề nào dưới đây đúng với hàm số \(y=|x+2|(x-1)^{2} ?\)
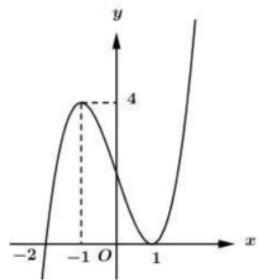
A. Hàm số đồng biến trên khoảng \((-\infty ;-1)\)
B. Hàm số nghịch biến trên khoảng (-1 ; 2)
C. Hàm số nghịch biến trên khoảng \((-\infty ;-2)\)
D. Hàm số đồng biến trên khoảng \((-2 ; 0)\)
Lời giải của giáo viên
 HocOn247.com
HocOn247.com
Ta có \(y=|x+2|(x-1)^{2}=\left|(x+2)(x-1)^{2}\right|\)
Dựa vào đồ thị hàm số \(y=(x+2)(x-1)^{2}\) suy ra đồ thị hàm số \(y=|(x+2)(x-1)^{2} |\) bằng cách:
+giữ nguyên phần đồ thị hàm số \(y=(x+2)(x-1)^{2}\)nằm trên trục Ox.
+Lấy đối xứng phần độ thị \(y=(x+2)(x-1)^{2}\) nằm dưới trục Ox qua Ox, bỏ đi phần đồ thị \(y=(x+2)(x-1)^{2}\) nằm dưới Ox
Ta được
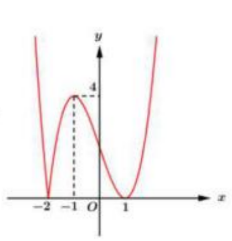
Dựa vào đồ thị hàm số trên ta thấy hàm số \(y=|x+2|(x-1)^{2}=\left|(x+2)(x-1)^{2}\right|\) đồng biến trên (-2;-1) và \((1;+\infty)\), nghịch biến trên \((-\infty ;-2) \text { và }(-1 ; 1)\)
Chỉ có đáp án C đúng.
CÂU HỎI CÙNG CHỦ ĐỀ
Xếp ngẫu nhiên 3 học sinh lớp A, 2 học sinh lớp B và 1 học sinh lớp C vào sáu ghế xếp quanh một bàn tròn (một học sinh ngồi đúng một ghế). Tính xác suất đề học sinh lớp C ngồi giữa 2 học sinh lớp .B
Trong không gian Oxyz, hai mặt phẳng \(x-4 y+2 z-7=0\,\, và \,\,2 x-2 y+z+4=0\) chứ hai mặt của hình lập phương. Thề tích khối lập phương đó là:
Trong không gian Oxyz, cho điểm A(1 ; 2 ; 3) và B(3 ; 4 ; 7) . Phương trình mặt phẳng trung trực của đoạn thẳng AB là:
Diện tích hình phẳng giới hạn bởi các đường \(y=x^{2}-x ; y=2 x-2 ; x=0 ; x=3\) được tính bởi công thức
Tính \( \lim\limits _{x \rightarrow 0^{+}} \frac{x-\sqrt{x}}{x}\)
Tập hợp các điềm biều diễn số phúrc z thỏa mãn \(|2 z-1|=1 \)là:
Tính thề tích V của khối trụ có chu vi đáy là \(2 \pi,\) chiều cao là \(\sqrt{2}\)
Cho hàm số y=f(x) thòa mãn f(2)=16 và \(\int\limits_{0}^{2} f(x) d x=4 .\) Tinh \(\int\limits_{0}^{1} x \cdot f^{\prime}(2 x) d x\)
Cho hinh chóp S . A B C D có \(S A \perp(A B C D)\), đáy ABCD là hình chữ nhật có \(A B=a \sqrt{3}, A D=a \sqrt{2}\) Khoảng cách giũra SD và BC bằng:
Trong không gian Oxyz, cho điểm M (1;-2; 3). Tọa độ điểm A là hình chiếu vuông góc của M trên măt phẳng (O y z) là:
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tai A, \(\widehat{ A B C}=30^{\circ}\). Tam giác SAB đều cạnh a và hình chiếu vuông góc cùa S lên mặt phẳng (A B C) là trung điểm của cạnh A B . Thề tích của khối chóp S .ABC là
Số lượng của loại vi khuẩn A trong môt phòng thí nghiệm ước tính theo công thức \(S_{t}=S_{0} \cdot 2^{t}\) trong đó \(S_{0}\) là số lượng vi khuẩn A ban đầu, \(S_{t}\) là số lượng vi khuẩn A có sau t phút. Biết sau 3 phút thì số lương vi khuẩn A là 625 nghìn con. Hỏi sau bao lâu, kề từ lúc ban đầu, số lượng vi khuẩn A là 10 triệu con?
Tim tâp xác định D của hàm số \(y=\left[x^{2}(x+1)\right]^{\frac{1}{2}}\)
Cho tứ diện ABCD có A B, A C, A D đôi một vuông góc và\(A B=2 a, A C=3 a, A D=4 a\). . Thể tích khối tứ diện là:




