Đề thi thử tốt nghiệp THPT QG môn Toán năm 2020 - Trường THPT chuyên Thái Bình
Đề thi thử tốt nghiệp THPT QG môn Toán năm 2020 - Trường THPT chuyên Thái Bình
-
Hocon247
-
50 câu hỏi
-
90 phút
-
65 lượt thi
-
Trung bình
Tham gia [ Hs Hocon247.com ] - Cộng Đồng Luyện Thi Trực Tuyến để được học tập những kiến thức bổ ích từ HocOn247.com
Hàm số \(y=\log _{\frac{\pi}{3}}(x-1)\) nghịch biến trên khoảng nào dưới đây?
Hàm số có TXĐ \(: D=(1 ;+\infty) \text { và } a=\frac{\pi}{3}<1\)
Nên hàm số nghịch biến trên \((1 ;+\infty)\)
Tìm họ nguyên hàm của hàm số \(f(x)=\sin 3 x\)
Ta có \(\int \sin 3 x d x=-\frac{1}{3} \cos 3 x+C\)
Cho tứ diện ABCD có A B, A C, A D đôi một vuông góc và\(A B=2 a, A C=3 a, A D=4 a\). . Thể tích khối tứ diện là:
Thể tích tứ diện có AB, AC, AD đôi một vuông góc là
\( V=\frac{1}{6} A B \cdot A C \cdot A D=\frac{1}{6} \cdot 2 a \cdot 3 a \cdot 4 a=4 a^{3}\)
Trong không gian Oxyz, một vecto chi phương của đường thẳng \(d: \frac{x-1}{1}=\frac{y+2}{-1}=\frac{z}{2}\) là
Đường thẳng \(d: \frac{x-1}{1}=\frac{y+2}{-1}=\frac{z}{2}\) có VTCP \( \vec{u}=(1 ;-1 ; 2)\)
Tập nghiệm của bất phưong trình \(\log _{\frac{1}{2}}(x-1) \geq 0\) là
Ta có \(\log _{\frac{1}{2}}(x-1) \geq 0 \Leftrightarrow\left\{\begin{array}{l} x-1>0 \\ x-1 \leq\left(\frac{1}{2}\right)^0 \end{array}\right.\)
\(\Leftrightarrow\left\{\begin{array}{l} x>1 \\ x-1 \leq 1 \end{array} \Leftrightarrow\left\{\begin{array}{l} x>1 \\ x \leq 2 \end{array} \Leftrightarrow 1<x \leq 2\right.\right.\)
Đồ thị trong hình vẽ dưới đây là đồ thị của hàm số nào?
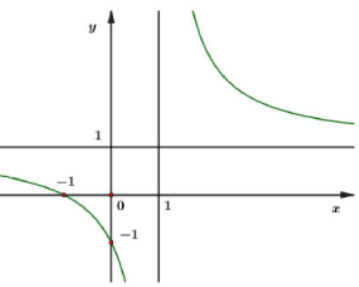
Dựa vào đồ thị hàm số ta thấy đồ thị hàm số có TCĐ là x=1 nên loại đáp án A.
Đồ thị hàm số đi qua điềm (-1; 0) và (0;-1) nên chọn B.
Hàm số nào dưới đây không có cực trị:
Chọn B vì hàm số \(\)luôn đồng biến (hoặc nghịch biến) trên các khoảng xác định nên không có cực trị.
Rút gọn biều thúrc \(P=\sqrt[3]{x^{5} \sqrt[4]{x}}\) với x>0
Với x>0 ta có:
\(P=\sqrt[3]{x^{5} \sqrt[4]{x}}=\sqrt[3]{x^{5} x^{\frac{1}{4}}}=\sqrt[3]{x^{5+\frac{1}{4}}}=\sqrt[3]{x^{\frac{21}{4}}}=x^{\frac{21}{4}:3}=x^{\frac{7}{4}}\)
Tim tâp xác định D của hàm số \(y=\left[x^{2}(x+1)\right]^{\frac{1}{2}}\)
Hàm số có số mũ không nguyên nên xác định khi
\(x^{2}(x+1)>0 \Leftrightarrow\left\{\begin{array}{l} x^{2} \neq 0 \\ x+1>0 \end{array} \Leftrightarrow\left\{\begin{array}{l} x \neq 0 \\ x>-1 \end{array}\right.\right.\)
Nếu \(\int\limits_{0}^{m}(2 x-1) d x=2\) thì m có giá trị bằng:
Ta có:
\(\int\limits_{0}^{m}(2 x-1) d x=2\)
\(\begin{array}{l} \left.\Leftrightarrow\left(x^{2}-x\right)\right|_{0} ^{m}=2 \Leftrightarrow m^{2}-m=2 \\ \Leftrightarrow m^{2}-m-2=0 \Leftrightarrow(m-2)(m+1)=0 \\ \Leftrightarrow\left[\begin{array}{l} m-2=0 \\ m+1=0 \end{array} \Leftrightarrow\left[\begin{array}{l} m=2 \\ m=-1 \end{array}\right.\right. \end{array}\)
Điều kiện cần và đủ đề hàm số \(y=a x^{4}+b x^{2}+c\) có hai điểm cực đại và một điểm cực tiểu là:
Hàm số có hai điểm cực đại và một điểm cực tiểu là \(\left\{\begin{array}{l} a<0 \\ b>0 \end{array}\right.\)
Modun của số phức z=2-3i bằng:
Ta có \(z=2-3 i \Rightarrow|z|=\sqrt{2^{2}+(-3)^{2}}=\sqrt{13}\)
Trong không gian Oxyz, cho điểm M (1;-2; 3). Tọa độ điểm A là hình chiếu vuông góc của M trên măt phẳng (O y z) là:
Tọa độ hình chiếu vuông góc của điểm M(1 ;-2 ; 3) trên mặt phẳng (Oyz) là A(0 ;-2 ; 3)
Cho \(\left(u_{n}\right)\) là cấp số nhân \(u_{1}=2, q=3\,. Tính\,\,u_{3}\)
Ta có \(\left\{\begin{array}{l} u_{1}=2 \\ q=3 \end{array} \Rightarrow u_{3}=u_{1} q^{2}=2.3^{2}=18\right.\)
Tập hợp các điềm biều diễn số phúrc z thỏa mãn \(|2 z-1|=1 \)là:
Gọi \(z=x+y i(x, y \in R)\)
Theo đề bài ta có:
\(|2 z-1|=1\)
\(\begin{array}{l} \Leftrightarrow|2(x+y i)-1|=1 \\ \Leftrightarrow|2 x-1+2 y i|=1 \\ \Leftrightarrow \sqrt{(2 x-1)^{2}+4 y^{2}}=1 \\ \Leftrightarrow(2 x-1)^{2}+4 y^{2}=1 \\ \Leftrightarrow 4\left(x-\frac{1}{2}\right)^{2}+4 y^{2}=1 \\ \Leftrightarrow\left(x-\frac{1}{2}\right)^{2}+y^{2}=\frac{1}{4} \end{array}\)
Vậy Quỹ tích của số phức z là đường tròn tâm \(\left(\frac{1}{2} ; 0\right)\) và bán kính \(R=\frac{1}{2}\)
Tìm tất cả các giá trị của m đẻ phương trình \(2^{2 x-1}+m^{2}-m=0\) có nghiệm.
Ta có \(2^{2 x-1}+m^{2}-m=0 \Leftrightarrow 2^{2 x-1}=-m^{2}+m\)
Phương trình có nghiệm \(\Leftrightarrow-m^{2}+m>0\Leftrightarrow m(m-1)<0 \Leftrightarrow 0<m<1\)
Hình lăng trụ đứng \(A B C . A^{\prime} B^{\prime} C^{\prime}\) có đáy ABC là tam giác vuông cân tại A có bao nhiêu mặt phẳng đối xứng?
Hình lăng trụ đứng \(A B C . A^{\prime} B^{\prime} C^{\prime}\) có đáy ABC là tam giác vuông cân tại A có 2 mặt phẳng đối xứng
Tính thề tích V của khối trụ có chu vi đáy là \(2 \pi,\) chiều cao là \(\sqrt{2}\)
Bán kính đường tròn đáy của khói trụ đã cho là: \(R=\frac{C}{2 \pi}=\frac{2 \pi}{2 \pi}=1\)
\(\Rightarrow\) Thể tích của khối trụ đã cho là: \(V=\pi R^{2} h=\pi \cdot 1^{2} \cdot \sqrt{2}=\sqrt{2} \pi\)
Số phức \(z=a+b i \quad(a, b \in \mathbb{R})\)thòa mãn \(2 z+1=\bar{z},\,\, có \,\,a+b\) bằng:
Số phức liên hợp \(\bar{z}=a-b i\)
Ta có:
\(\begin{array}{l} \Rightarrow 2 z+1=\bar{z} \\ \Leftrightarrow 2(a+b i)+1=a-b i \\ \Leftrightarrow 2 a+1+2 b i=a-b i \\ \Leftrightarrow\left\{\begin{array}{l} 2 a+1=a \\ 2 b=-b \end{array} \Leftrightarrow\left\{\begin{array}{l} a=-1 \\ b=0 \end{array}\right.\right. \\ \Rightarrow a+b=-1+0=-1 \end{array}\)
Cho hàm số \(f(x)=x^{3}+\left(m^{2}+1\right) x+m^{2}-2\) vói m là tham số thực. Tìm tất cả các giá trị của m để hàm số có giá trị nhỏ nhất trên đoạn [0; 2] bằng 7.
Ta có \(f(x)=x^{3}+\left(m^{2}+1\right) x+m^{2}-2\Rightarrow f^{\prime}(x)=3 x^{2}+m^{2}+1>0 \quad \forall m\)
Vậy hàm số đồng biến trên \(\mathbb{R}\)
\(\begin{array}{l} \Rightarrow \mathop {\min }\limits_{{\rm{[0;2]}}} f\left( x \right)=f(0)=7 \\ \Leftrightarrow m^{2}-2=7 \\ \Leftrightarrow m^{2}=9 \\ \Leftrightarrow m=\pm 3 \end{array}\)
Trong không gian Oxyz, cho điểm A(1 ; 2 ; 3) và B(3 ; 4 ; 7) . Phương trình mặt phẳng trung trực của đoạn thẳng AB là:
Gọi I là trung\(\Rightarrow I(1;3;5)\) điểm AB
\(\overrightarrow{A B}=(2 ; 2 ; 4)\). Mặt phẳng vuông góc với AB nên nhận \(\overrightarrow {AB}\) làm vec tơ pháp tuyến.
Phương trình mặt phẳng trung trực đi qua điểm I và có vec tơ pháp tuyến \(\overrightarrow {AB}\) là
\((\alpha):2( x-2)+2(y-3)+4(z-5)=0 \Leftrightarrow x+y+2 z-15=0\)
Hình nón có đường sinh \(l=2 a\) và hợp với đáy góc \(a=60^{\circ}\). Diện tích toàn phần của hình nón bằng:
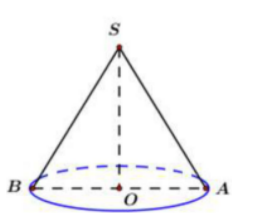
Đường sinh hợp với đáy góc \(\alpha=60^{\circ} \Rightarrow \widehat { S A O}=60^{\circ}\)
\(\begin{array}{l} \Rightarrow O A=S A \cdot \cos 60^{\circ}=2 a \cdot \frac{1}{2}=a \\ \Rightarrow S_{t p}=\pi R l+\pi R^{2}=\pi \cdot a \cdot 2 a+\pi a^{2}=3 \pi a^{2} \end{array}\)
Trên giá sách có 4 quyển sách toán, 3 quyển sách lý, 2 quyển sách hóa (các quyển sách cùng đôi một khác nhau). Hỏi có bao nhiêu cách lấy ra 3 quyển sách sao cho ít nhất một quyển sách toán?
Tổng số quyên sách trên giá sách là 9 quyển.
Số cách lấy được 3 quyển sách bất kì trên giá sách là \(C_{9}^{3}=84\) cách.
Số cách lấy được 3 quyền sách mà trong đó không có quyển sách Toán nào là: \(C_{3}^{3}+C_{3}^{2} C_{2}^{1}+C_{3}^{1} C_{2}^{2}=10\) cách.
\(\Rightarrow\) Số cách lấy được 3 quyển sách trong đó có ít nhất 1 quyền sách toán là: 84 - 10 = 74 cách.
Tính \( \lim\limits _{x \rightarrow 0^{+}} \frac{x-\sqrt{x}}{x}\)
\(\lim \limits _{x \rightarrow 0^{+}} \frac{x-\sqrt{x}}{x}=\lim \limits _{x \rightarrow 0^{+}} \frac{x^{2}-x}{x(x+\sqrt{x})}=\lim \limits_{x \rightarrow 0^{+}} \frac{x-1}{x+\sqrt{x}}\)
Vì \(\lim \limits_{x \rightarrow 0^{+}}(x-1)=-1 ; \lim\limits _{x \rightarrow 0^{+}}(x+\sqrt{x})=0^{+} \Rightarrow \lim\limits _{x \rightarrow 0^{+}} \frac{x-\sqrt{x}}{x}=-\infty\)
Cho số thực x thỏa mãn \(2^{x^{2}} \cdot 3^{x+1}=1\). Mệnh đề nào dưới đây đúng?
\(\begin{array}{l} \text { Ta } \operatorname{có}: 2^{x^{2}} \cdot 3^{x+1}=1 \\ \Leftrightarrow \log _{2}\left(2^{x^{2}} \cdot 3^{x+1}\right)=\log _{2} 1 \\ \Leftrightarrow \log _{2} 2^{x^{2}}+\log _{2} 3^{x+1}=0 \\ \Leftrightarrow x^{2}+(x+1) \log _{2} 3=0 \end{array}\)
Diện tích hình phẳng giới hạn bởi các đường \(y=x^{2}-x ; y=2 x-2 ; x=0 ; x=3\) được tính bởi công thức
Diện tích hình phẳng giới hạn bởi các đường \(y=x^{2}-x ; y=2 x-2 ; x=0 ; x=3\) được tính bởi công thức
\(S=\int_{0}^{3}\left|x^{2}-x-(2 x-2)\right| d x=\int_{0}^{3}\left|x^{2}-3 x+2\right| d x\)
Trong không gian Oxyz, hai mặt phẳng \(x-4 y+2 z-7=0\,\, và \,\,2 x-2 y+z+4=0\) chứ hai mặt của hình lập phương. Thề tích khối lập phương đó là:
Mặt phẳng \((P): 4 x-4 y+2 z-7=0 \text { có } \text { VTPT là: } \overrightarrow{n_{P}}=(4 ;-4,2)=2(2 ;-2 ; 1)\)
Mặt phẳng \((Q): 2 x-2 y+z+4=0 \text { có VTPT là: } \overrightarrow{n_{Q}}=(2 ;-2 ; 1)\)
\(\Rightarrow \overrightarrow{n_{p}} / / \overrightarrow{n_{Q}} \Rightarrow(P) / /(Q)\)
Lấy \(A(0 ; 2 ; 0) \in(Q)\)
\(\Rightarrow d((P) ;(Q))=d(A ;(P))=\frac{|4.0-4.2+2.0-7|}{\sqrt{4^{2}+(-4)^{2}+2^{2}}}=\frac{15}{6}=\frac{5}{2}\)
Mà hai mặt phẳng (P), (Q) chứ hai mặt của hình lập phương đã cho\(\Rightarrow\)Độ dài cạnh của hình lập phương \(d((P) ;(Q))=\frac{5}{2}\)
\(\Rightarrow V=\left(\frac{5}{2}\right)^{3}=\frac{125}{8}\)
Cho hàm số y=f(x) liên tục trên \(\mathbb{R}\) và có bảng biến thiên như sau:
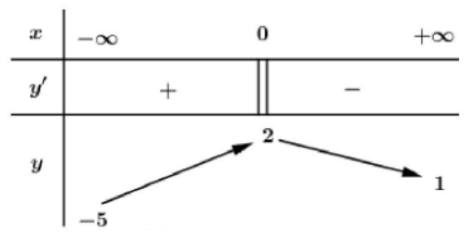
Có bao nhiêu giá trị nguyên của m để phương trình f(x)=m có nghiệm duy nhất?
Phương trình \(f(x)=m\) có nghiệm duy nhất \(\Leftrightarrow \) đường thẳng y=m cắt đồ thị hàm số y=f(x) tại 1 điểm duy nhất.

Dựa vào bảng biến thiên nhận thấy
Đường thẳng y=m cắt đồ thị hàm số y=f(x) tại 1 điểm duy nhất.\(\Leftrightarrow-5<m \leq 1\)
Mà m nguyên \(\Rightarrow m\{-4 ;-3 ;-2 ;-1 ; 0 ; 1\}\)
Vậy có 6 giá trị m thỏa mãn yêu cầu bài toán.
Trong không gian Oxyz, cho hai mặt phẳng \((\alpha): x+y-z+1=0\,\,và \,\,(\beta):-2 x+m y+2 z-2=0\) Tìm m để \((\alpha)\) song song với \((\beta)\)
Mặt phẳng \((\alpha): x+y-z+1=0 \text { có VTPT là: } \overrightarrow{n_{\alpha}}=(1 ; 1 ;-1)\)
Mặt phẳng \((\beta):-2 x+m y+2 z-2=0 \text { có VTPT là: } \overrightarrow{n_{\beta}}=(-2 ; m ; 2)\)
\(\Rightarrow(\alpha) / /(\beta) \Leftrightarrow \frac{-2}{1}=\frac{m}{1}=\frac{2}{-1} \neq \frac{-2}{1}(\text { vô lý })\)
Vậy không tồn tại góa trị m thỏa yêu cầu bài toán.
Cho a, b, c là các số thực dương khác 1. Hình vẽ bên là đồ thị của ba hàm số \(y=\log _{a} x, y=\log _{b} x, y=\log _{c} x .\)Mệnh đề nào dưới đây đúng?
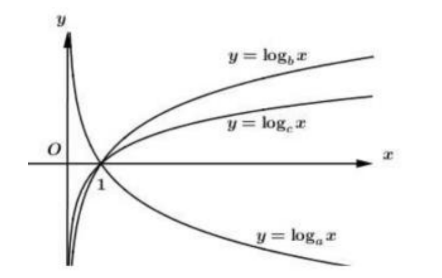
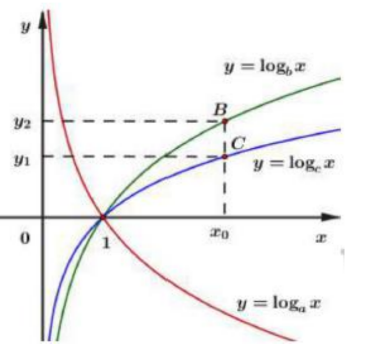
Dựa vào đồ thị hàm số ta thấy hàm số \(y=\log _{a} x\) là hàm số nghich biến \(\Rightarrow 0<a<1\).
Hàm số \(y=\log _{c} x, y=\log _{b} x\) là các hàm số đồng biền \(\Rightarrow\left\{\begin{array}{l}b>1 \\ c>1\end{array}\right.\)
Ta lấy điểm \(B\left(x_{0} ; y_{2}\right)\) thuộc đồ thị hàm số \(y=\log _{b} x\) và điểm \(C\left(x_{0} ; y_{1}\right)\) thuộc đồ thị hàm số \(y=\log _{c} x\) như hình vẽ.
Khi đó ta có:
\(\left\{\begin{array}{l}y_{2}=\log _{b} x_{0} \\ y_{1}=\log _{c} x_{0}\end{array} \Leftrightarrow\left\{\begin{array}{l}x_{0}=b^{y_{2}} \\ x_{0}=c^{y_{1}}\end{array} \Leftrightarrow b^{y_{2}}=c^{y_{1}}\right.\right.\)
\(\begin{array}{l} \text { Mà }\left\{\begin{array}{l} y_{1}<y_{2} \\ b>1 \quad \Rightarrow b<c \\ c>1 \end{array}\right. \\ \Rightarrow a<1<b<c \end{array}\)
Cho hinh chóp S . A B C D có \(S A \perp(A B C D)\), đáy ABCD là hình chữ nhật có \(A B=a \sqrt{3}, A D=a \sqrt{2}\) Khoảng cách giũra SD và BC bằng:
Vì ABCD là hình chũr nhật \(\Rightarrow BC//A D \Rightarrow BC//(S A D) \supset S D\)
\(\Rightarrow d(S D ; B C)=d(B C ;(S A D))=d(B ;(S A D))\)
Ta có \(\left\{\begin{array}{l} A B \perp A D(g t) \\ A B \perp S A(S A \perp(A B C D)) \end{array} \Rightarrow A B \perp(S A D)\right.\)
\(\begin{array}{l} \Rightarrow d(B ;(S A D))=A B=a \sqrt{3} \\ \text { Vậy } d(S D, B C)=a \sqrt{3} \end{array}\)
Xếp ngẫu nhiên 3 học sinh lớp A, 2 học sinh lớp B và 1 học sinh lớp C vào sáu ghế xếp quanh một bàn tròn (một học sinh ngồi đúng một ghế). Tính xác suất đề học sinh lớp C ngồi giữa 2 học sinh lớp .B
Xếp 6 học sinh quanh một bàn tròn \(\Rightarrow n(\Omega)=5 !=120\)
Gọi A là biến cố: "Học sinh lớp C ngồi giữa 2 học sinh lớp B". Cố định học sinh lớp C, xếp 2 học sinh lớp B ngồi hai bên học sinh lớp C có 2!=2 cách.
Xếp 3 học sinh lớp A vào 3 ghế còn lại có 3! = 6 cách. \(\Rightarrow n(A)=2.6=12\)
Vậy xác suất của biến cố A là: \(P(A)=\frac{n(A)}{n(\Omega)}=\frac{12}{120}=\frac{1}{10}\)
Cho hàm số y=f(x) là hàm đa thức bậc ba và có đồ thị như hinh vẽ bên. Khằng định nào sau đây sai?
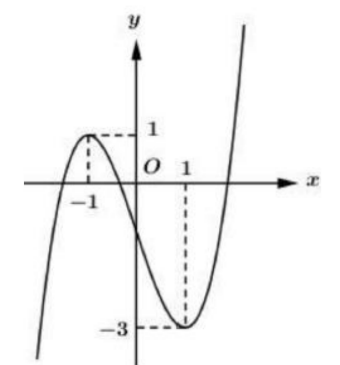
Dựa vào đồ thị hàm số nhận thấy:
Hàm số đồng biến trên \((-\infty ;- 1) \, và\,\,(1 ;+\infty)\)
Hàm số nghịch biến trên (-1 ; 1)
Vậy đáp án D sai.
Biết \(\int\limits_{0}^{1} \frac{3 x-1}{x^{2}+6 x+9} d x=3 \ln \frac{a}{b}-\frac{5}{6},\) trong đó a, b là các số nguyên dương và \(\frac{a}{b}\) tối gian. Khi dó \(a^{2}-b^{2}\) bằng
ta có
\(\begin{array}{l} \frac{3 x-1}{x^{2}+6 x+9}=\frac{3 x-1}{(x+3)^{2}}=\frac{A}{(x+3)^{2}}+\frac{B}{x+3} \\ \Leftrightarrow \frac{3 x-1}{x^{2}+6 x+9}=\frac{A+B(x+3)}{(x+3)^{2}} \\ \Leftrightarrow \frac{3 x-1}{x^{2}+6 x+9}=\frac{B x+A+3 B}{(x+3)^{2}} \end{array}\)
Dùng đồng nhất hệ số ta có
\(\left\{\begin{array}{l} B=3 \\ A+3 B=-1 \end{array} \Leftrightarrow\left\{\begin{array}{l} B=3 \\ A=-10 \end{array}\right.\right.\)
\(\begin{array}{l} \Rightarrow \frac{3 x-1}{x^{2}+6 x+9}=-\frac{10}{(x+3)^{2}}+\frac{3}{x+3} \\ \Rightarrow \int\limits_{0}^{1} \frac{3 x-1}{x^{2}+6 x+9} d x=-10 \int\limits_{0}^{1} \frac{d x}{(x+3)^{2}}+3 \int\limits_{0}^{1} \frac{d x}{x+3} \\ \Leftrightarrow \int\limits_{0}^{1} \frac{3 x-1}{x^{2}+6 x+9} d x=\left.10 \cdot \frac{1}{x+3}\right|_{0} ^{1}+\left.3 \ln |x+3|\right|_{0} ^{1} \\ \Leftrightarrow \int\limits_{0}^{1} \frac{3 x-1}{x^{2}+6 x+9} d x=10\left(\frac{1}{4}-\frac{1}{3}\right)+3(\ln 4-\ln 3) \\ \Leftrightarrow \int\limits_{0}^{1} \frac{3 x-1}{x^{2}+6 x+9} d x=3 \ln \frac{4}{3}-\frac{5}{6} \end{array}\)
\(\Rightarrow a=4, b=3 \Rightarrow a^{2}-b^{2}=4^{2}-3^{2}=7\)
Cho hàm số y=f(x) thóa mãn\(f(2)=-\frac{4}{19}\,\, và \,\,f^{\prime}(x)=x^{3} f^{2}(x) \forall x \in \mathbb{R} .\) Giá trị của f(1) bằng:
Từ đề bài ta có \(f^{\prime}(x)=x^{3} f^{2}(x) \forall x \in \mathbb{R} \Leftrightarrow \frac{f^{\prime}(x)}{f^{2}(x)}=x^{3} \forall x \in \mathbb{R}\)
Lấy nguyên hàm hai vế ta được
\(\int \frac{f^{\prime}(x)}{f^{2}(x)} d x=\int x^{3} d x \Leftrightarrow-\frac{1}{f(x)}=\frac{x^{4}}{4}+C\)
Mà \(f(2)=-\frac{4}{19} \Leftrightarrow-\frac{1}{f(2)}=4+C \Leftrightarrow \frac{19}{4}=4+C \Leftrightarrow C=\frac{3}{4}\)
\(\Rightarrow -\frac{1}{f(x)}=\frac{x^{4}}{4}+\frac{3}{4}\)
Với x=1 ta có \(-\frac{1}{f(1)}=\frac{1}{4}+\frac{3}{4}=1 . \text { Vậy } f(1)=-1\)
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tai A, \(\widehat{ A B C}=30^{\circ}\). Tam giác SAB đều cạnh a và hình chiếu vuông góc cùa S lên mặt phẳng (A B C) là trung điểm của cạnh A B . Thề tích của khối chóp S .ABC là
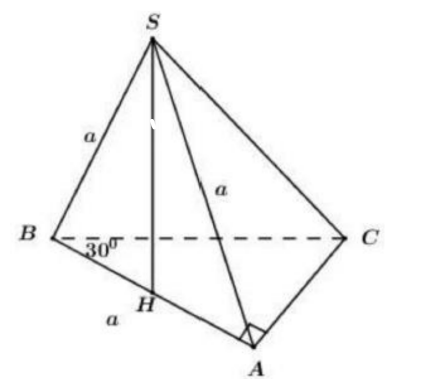
Gọi H là trung điểm AB\(A B \Rightarrow S H \perp(A B C)\)
Tam giác SAB đều cạnh a\(a \Rightarrow S H=\frac{a \sqrt{3}}{2}\)
Xét tam giác vuông ABC:
\(A C=A B \cdot \tan 30^{\circ}=\frac{a \sqrt{3}}{3} \Rightarrow S_{\mathrm{ABC}}=\frac{1}{2} A B \cdot A C=\frac{1}{2} \cdot a \cdot \frac{a \sqrt{3}}{3}=\frac{a^{2} \sqrt{3}}{6}\)\(\Rightarrow V_{S, A B C}=\frac{1}{3} S H S_{\Delta A B C}=\frac{1}{3} \cdot \frac{a \sqrt{3}}{2} \cdot \frac{a^{2} \sqrt{3}}{6}=\frac{a^{3}}{12}\)
Cho hình chóp S.ABCD có đáy là hình vuông cạnh \(2\sqrt{2}\). Canh bên SA vuông góc với mặt phẳng đáy và SA=3 . Mặt phẳng \((\alpha)\) qua A và vuông góc vói SC cắt canh SB, SC, SD lần lươt tai M, N, P . Thể tích V của khối cầu ngoại tiếp tứ diện CMNP.
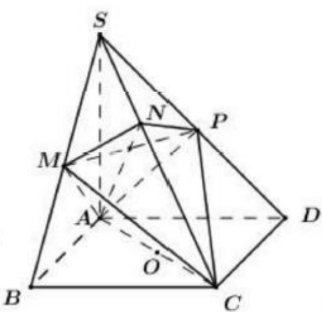
Ta có
\(\begin{array}{l} \left\{\begin{array}{l} B C \perp A B \\ B C \perp S A \end{array} \Rightarrow B C \perp(S A B) \Rightarrow B C \perp A M\right. \\ \left\{\begin{array}{l} A M \perp B C \\ A M \perp S C \end{array} \Rightarrow A M \perp(S B C) \Rightarrow A M \perp M C\right. \end{array}\)
\(\Rightarrow \widehat{ A M C}=90^{\circ}\) hay điểm M thuộc mặt cầu đường kính AC.
Tương tự ta có \(A P \perp(S C D) \Rightarrow A P \perp P C \Rightarrow \widehat{ A P C}=90^{\circ}\)
hay P thuộc măt cầu đường kính AC.
lại có \(A N \perp S C \Rightarrow \widehat {A N C}=90^{\circ}\)hay N thuộc mặt cầu đường kính AC.
Do đó CMNP nội tiếp khối cầu đường kính AC hay khối cầu ngoại tiếp tứ diện CMNP có bán kính \(R=\frac{1}{2} A C=\frac{1}{2} \cdot 2 \sqrt{2} \cdot \sqrt{2}=2\)
Thể tích cần tìm là \(V=\frac{4}{3} \pi R^{3}=\frac{4}{3} \pi \cdot 2^{3}=\frac{32 \pi}{3}\)
Cho hàm số y=f(x) thòa mãn f(2)=16 và \(\int\limits_{0}^{2} f(x) d x=4 .\) Tinh \(\int\limits_{0}^{1} x \cdot f^{\prime}(2 x) d x\)
Đặt \(t=2 x \Rightarrow d t=2 d x\)
Đổi cận \(\left\{\begin{array}{l} x=0 \Rightarrow t=0 \\ x=1 \Rightarrow t=2 \end{array}\right.\)
Khi đó \(\int\limits_{0}^{1} x \cdot f^{\prime}(2 x) d x=\frac{1}{4} \int\limits_{0}^{2} t f^{\prime}(t) d t\)
Đặt \(\left\{\begin{array}{l} u=t \\ d v=f^{\prime}(t) d t \end{array} \Leftrightarrow\left\{\begin{array}{l} d u=d t \\ v=f(t) \end{array}\right.\right.\)
\(\begin{array}{c} \Rightarrow \int\limits_{0}^{2} t f^{\prime}(t) d t=\left.t f(t)\right|_{0} ^{2}-\int\limits_{0}^{2} f(t) d t \\ =2 f(2)-\int\limits_{0}^{2} f(x) d x \\ =2.16-4=28 \end{array}\)
Vậy \(\int\limits_{0}^{1} x \cdot f^{\prime}(2 x) d x=\frac{1}{4} \cdot 28=7\)
Số lượng của loại vi khuẩn A trong môt phòng thí nghiệm ước tính theo công thức \(S_{t}=S_{0} \cdot 2^{t}\) trong đó \(S_{0}\) là số lượng vi khuẩn A ban đầu, \(S_{t}\) là số lượng vi khuẩn A có sau t phút. Biết sau 3 phút thì số lương vi khuẩn A là 625 nghìn con. Hỏi sau bao lâu, kề từ lúc ban đầu, số lượng vi khuẩn A là 10 triệu con?
Sau 3 phút thì số lượng vi khuần A là 625 nghìn con.
\(\Rightarrow S_{3}=S_{0} \cdot 2^{3} \Leftrightarrow 625=S_{0} \cdot 8 \Leftrightarrow S_{0}=\frac{625}{8} \)(Nghìn con)
Goi t là thời điềm số lượng vi khuần A là 10 triệu con, khi đó ta có:
\(S_{t}=S_{0} \cdot 2^{t}
\Leftrightarrow 10000=\frac{625}{8} \cdot 2^{t}
\Leftrightarrow 2^{t}=128\Leftrightarrow t=\log _{2} 128=7\)
Vậy sau 7 phút thì số lượng vi khuẩn A là 10 triệu con.
Cho hàm số f(x) xác định và liên tục trên \(\mathbb{R} \backslash\{-1\},\) có bång biên thiên nhur sau:
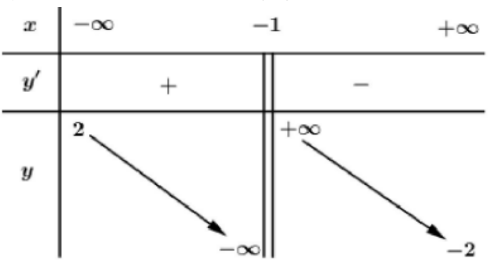
Höi đồ thị hàm số \(y=\frac{1}{f(x)}\) có tất cả bao nhiêu đường tiệm cận đứng và tiệm cận ngang?
Từ bảng biến thiên ta có:
\(\lim \limits_{x \rightarrow-\infty} y=2, \lim\limits _{x \rightarrow+\infty} y=-2, \lim\limits _{x \rightarrow-1} y=-\infty, \lim\limits _{x \rightarrow-1^+} y=+\infty\)
Đặt \(y=g(x)=\frac{1}{f(x)}\) ta có:
\(\lim\limits _{x \rightarrow+\infty} g(x)=\lim \limits_{x \rightarrow+\infty} \frac{1}{f(x)}=-\frac{1}{2} \Rightarrow y=-\frac{1}{2}\) là TCN của đồ thị hàm số \(y=g(x)=\frac{1}{f(x)}\)
\(\lim\limits _{x \rightarrow-\infty} g(x)=\lim \limits_{x \rightarrow-\infty} \frac{1}{f(x)}=\frac{1}{2} \Leftrightarrow y=\frac{1}{2}\) là TCN của đồ thị hàm số \(y=g(x)=\frac{1}{f(x)}\)
\(\lim \limits_{x \rightarrow-1} g(x)=\lim\limits _{x \rightarrow-1} \frac{1}{f(x)}=0 \Rightarrow x=-1\) không là TCĐ cùa đồ thị hàm số \(y=g(x)=\frac{1}{f(x)}\)
Xét phương trình f(x)=0, dựa vào BBT ta thấy phương trình có 2 nghiệm phân biệt thỏa mãn khác - 1 .
Vậy đồ thị hàm số \(y=g(x)=\frac{1}{f(x)}\) có 2 TCĐ
Vậy đồ thị hàm số .\(y=g(x)=\frac{1}{f(x)}\) có 4 tiệm cận.
Cho hàm số \(y=(x+2)(x-1)^{2}\) có đồ thị như hình vẽ. Hỏi mệnh đề nào dưới đây đúng với hàm số \(y=|x+2|(x-1)^{2} ?\)
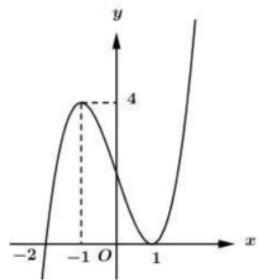
Ta có \(y=|x+2|(x-1)^{2}=\left|(x+2)(x-1)^{2}\right|\)
Dựa vào đồ thị hàm số \(y=(x+2)(x-1)^{2}\) suy ra đồ thị hàm số \(y=|(x+2)(x-1)^{2} |\) bằng cách:
+giữ nguyên phần đồ thị hàm số \(y=(x+2)(x-1)^{2}\)nằm trên trục Ox.
+Lấy đối xứng phần độ thị \(y=(x+2)(x-1)^{2}\) nằm dưới trục Ox qua Ox, bỏ đi phần đồ thị \(y=(x+2)(x-1)^{2}\) nằm dưới Ox
Ta được
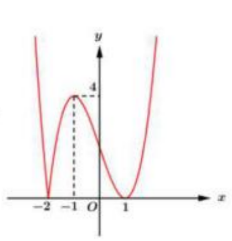
Dựa vào đồ thị hàm số trên ta thấy hàm số \(y=|x+2|(x-1)^{2}=\left|(x+2)(x-1)^{2}\right|\) đồng biến trên (-2;-1) và \((1;+\infty)\), nghịch biến trên \((-\infty ;-2) \text { và }(-1 ; 1)\)
Chỉ có đáp án C đúng.
Viết phương trình tiếp tuyến của đồ thị hàm số \(y=\frac{x+3}{x-1},\) biết tiếp tuyến đó tạo với hai trục tọa độ một tam giác vuông cân.
\(\mathrm{TXD}: D=R \backslash\{1\}\)
\(y^{\prime}=\frac{-4}{(x-1)^{2}}\)
Goi \(M\left(x_{0} ; y_{0}\right)\) là điểm thuộc đồ thị hàm số, phương trình tiếp tuyến của đồ thị hàm số tại M là:
\((d):y=\frac{-4}{\left(x_{0}-1\right)^{2}}\left(x-x_{0}\right)+\frac{x_{0}+3}{x_{0}-1}\)
Gọi \(A=d \cap O x\)
Cho y=0 ta có:
\(\begin{array}{l} \Rightarrow 0=\frac{-4}{\left(x_{0}-1\right)^{2}}\left(x-x_{0}\right)+\frac{x_{0}+3}{x_{0}-1} \\ \Leftrightarrow 0=-4\left(x-x_{0}\right)+\left(x_{0}+3\right)\left(x_{0}-1\right) \\ \Leftrightarrow 0=-4 x+4 x_{0}+x_{0}^{2}+2 x_{0}-3 \\ \Leftrightarrow x=\frac{x_{0}^{2}+6 x_{0}-3}{4} \\ \Rightarrow A\left(\frac{x_{0}^{2}+6 x_{0}-3}{4} ; 0\right) \Rightarrow O A=\frac{\left|x_{0}^{2}+6 x_{0}-3\right|}{4} \end{array}\)
Gọi \(B=d \cap O y\)
Cho x=0
\(\begin{array}{l} \Rightarrow y=\frac{4 x_{0}}{\left(x_{0}-1\right)^{2}}+\frac{x_{0}+3}{x_{0}-1}=\frac{4 x_{0}+\left(x_{0}+3\right)\left(x_{0}-1\right)}{\left(x_{0}-1\right)^{2}} \\ =\frac{4 x_{0}+x_{0}^{2}+2 x_{0}-3}{\left(x_{0}-1\right)^{2}}=\frac{x_{0}^{2}+6 x_{0}-3}{\left(x_{0}-1\right)^{2}} \\ \Rightarrow B\left(0 ; \frac{x_{0}^{2}+6 x_{0}+3}{\left(x_{0}-1\right)^{2}}\right) \Rightarrow O B=\frac{\left|x_{0}^{2}+6 x_{0}-3\right|}{\left(x_{0}-1\right)^{2}} \end{array}\)
Vì tam giác OAB vuông cân tại O nên O A=OB.
\(\begin{array}{l} \Leftrightarrow \frac{\left|x_{0}^{2}+6 x_{0}-3\right|}{4}=\frac{\left|x_{0}^{2}+6 x_{0}-3\right|}{\left(x_{0}-1\right)^{2}} \\ \Leftrightarrow\left|x_{0}^{2}+6 x_{0}-3\right|\left(\frac{1}{4}-\frac{1}{\left(x_{0}-1\right)^{2}}\right)=0 \\ \Leftrightarrow \frac{1}{4}-\frac{1}{\left(x_{0}-1\right)^{2}}=0 \end{array}\)
(Do \(A \neq B \text { nên } x_{0}^{2}+6 x_{0}-3 \neq 0)\)
\(\Leftrightarrow\left(x_{0}-1\right)^{2}=4 \Leftrightarrow\left[\begin{array}{l} x_{0}-1=2 \\ x_{0}-1=-2 \end{array} \Leftrightarrow\left[\begin{array}{l} x_{0}=3 \\ x_{0}=-1 \end{array}(t m)\right.\right.\)
Với \(x_{0}=3\) thì phương trình tiếp tuyến là \(y=-1(x-3)+3 \Leftrightarrow y=-x+6\)
Với \(x_{0}=-1\) thì phương tình tiếp tuyến là \(y=-1(x+1)-1 \Leftrightarrow y=-x-2\)
Cho hình chóp tứ giác đều S.ABCD có đáy là hình vuông tâm O; cạnh a. Goi M, N lần lượt là trung điểm của SA và BC. Góc giữa đường thằng M N và mặt phẳng (A B C D) bằng \(60^{\circ} .\) Tính cos của góc giũa đương thằng MN và măt phẳng (SBD) ?
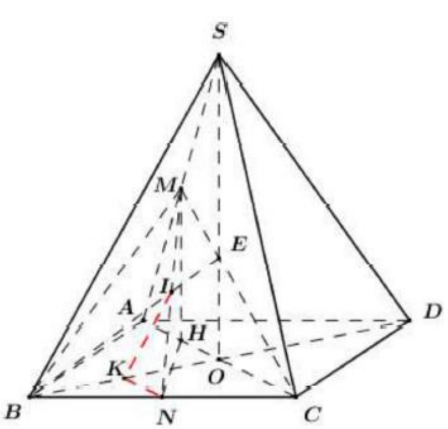
Goi H là trung điểm của OA ta có M H//S O \(\Rightarrow M H \perp(A B C D)\)
\(\Rightarrow H N\) là hinh chiếu của MN lên (A B C D) \\(\Rightarrow \widehat{(M N ;(A B C D))}=\widehat{M N ; H N}=\widehat{ M N H}=60^{\circ}\)
Xét tam giác CHN có: \(C N=\frac{1}{2} B C=\frac{a}{2}, C H=\frac{3}{4} A C=\frac{3 a \sqrt{2}}{4}, \widehat{{ H C N}}=45^{\circ}\)
\(\Rightarrow H N^{2}=C H^{2}+C N^{2}-2 C H \cdot C N \cdot \cos 45^{0}\)
\(H N^{2}=\frac{9 a^{2}}{8}+\frac{a^{2}}{4}-2 \cdot \frac{3 a \sqrt{2}}{4} \cdot \frac{a}{2} \cdot \frac{\sqrt{2}}{2}\\
H N^{2}=\frac{5 a^{2}}{8} \Rightarrow H N=\frac{a \sqrt{10}}{4}\)
Xét tam giác vuông MNH có: \(M N=\frac{N H}{\cos 60^{\circ}}=\frac{a \sqrt{10}}{2}\)
Trong (SAC) gọi \(E=C M \cap S O \Rightarrow(M B C) \cap(S B D)=B E\)
Trong (M B C) goi \(I=M N \cap B E \Rightarrow I=M N \cap(S B D)\)
Gọi K là trung điểm của O B \(\Rightarrow N K // O C\)
Ta có: \(\left\{\begin{array}{l}O C \perp B D \\ O C \perp S O\end{array} \Rightarrow O C \perp(S B D) \Rightarrow N K \perp(S B D)\right.\)
\(\Rightarrow I K\) là hinh chiếu của IN lên (S B D) \(\Rightarrow \widehat{(M N ;(S B D))}=\widehat{(I N ;(S B D))}=\widehat{(I N ; I K)}=\widehat{ N I K}\)
Ta có \(N K=\frac{1}{2} O C=\frac{a \sqrt{2}}{4}\)
Áp dụng định lí Menelaus trong tam giác MAC ta có:
\(\frac{E M}{E C} \cdot \frac{O C}{O A} \cdot \frac{S A}{S M}=1 \Leftrightarrow \frac{E M}{E C} \cdot 1.2=1 \Leftrightarrow \frac{E M}{E C}=\frac{1}{2}\)
Áp dụng định lý Menelaus trong tam giác MNC ta có:
\(\frac{I M}{I N} \cdot \frac{B N}{B C} \cdot \frac{E C}{E M}=1 \Leftrightarrow \frac{I M}{I N} \cdot \frac{1}{2} \cdot 2=1 \Leftrightarrow I M=I N\)
\(\Rightarrow I N=\frac{1}{2} M N=\frac{a \sqrt{10}}{4}\)
Xét tam giác vuông INK có : \(\sin \widehat{ N I K}=\frac{N K}{I N}=\frac{a \sqrt{2}}{4}: \frac{a \sqrt{10}}{4}=\frac{1}{\sqrt{5}}\)
\(\cos\widehat{ N I K}=\sqrt{1-\sin ^{2}\widehat{ N I K}}=\sqrt{1-\frac{1}{5}}=\frac{2 \sqrt{5}}{5}\)
Cho y=f(x) là hàm đa thức bậc 3 và có đồ thị nhu hình vẽ bên. Hỏi phương trình \(f[f(\cos x)-1]=0\) có bao nhiêu nghiệm thuộc đoan \([0 ; 3 \pi] ?\)
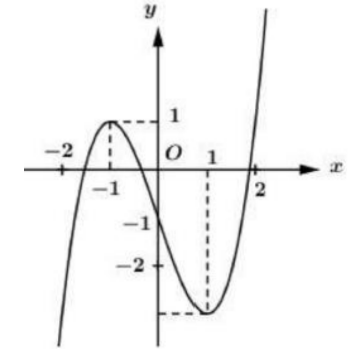
Đặt \(t=f(\cos x)-1\) phương trình trở thành:\(f(t)=0\)
\(\text { Với } x \in[0 ; 3 \pi] \Rightarrow-1 \leq \cos x \leq 1 \Leftrightarrow-3 \leq f(\cos x) \leq 1 \Rightarrow-4 \leq f(\cos x)-1 \leq 0 \Rightarrow t \in[-4 ; 0]\)
Dựa vào đồ thị hàm số ta thấy \(f(t)=1 \Leftrightarrow\left[\begin{array}{l}t=t_{1} \in(-2 ;-1) \\ t=t_{2} \in(-1 ; 0) \\ t=t_{3} \in(1 ; 2)(k t m)\end{array}\right.\)
\(+ Với \,t=t_{1} \Rightarrow f(\cos x)-1=t_{1} \Leftrightarrow f(\cos x)=t_{1}+1 \in(-1 ; 0)\)
Dụa vào đồ thị hàm số ta có: \(f(\cos x)=t_{1}+1 \in(-1 ; 0) \Leftrightarrow\left[\begin{array}{l}\cos x=a_{1} \in(-2 ;-1)(\text { Vô nghiệm }) \\ \cos x=a_{2} \in(-1 ; 0)(1) \\ \cos x=a_{3} \in(1 ; 2)(\text { Vô nghiệm })\end{array}\right.\)
Trên đoạn \([0 ; 3 \pi]\) phương trình (1) có 3 nghiệm phân biệt.
\(+\text { Với } t=t_{2} \Rightarrow f(\cos x)-1=t_{2} \Leftrightarrow f(\cos x)=t_{2}+1 \in(0 ; 1)\)
Dụa vào đồ thị hàm số ta có: \(f(\cos x)=t_{2}+1 \in(0 ; 1) \Leftrightarrow\left[\begin{array}{l}{\left.\cos x=b_{1} \in(-2 ;-1)(\text { Vô nghiệm })\right.} \\ \cos x=b_{2} \in(0 ; 1)(2) \\ \cos x=b_{3} \in(1 ; 2)(\text { Vô nghiệm })\end{array}\right.\)
Trên đoạn \([0 ; 3 \pi]\) phương trình (2) có 3 nghiệm phân biệt.
Vậy phương trình đã cho có 6 nghiệm phân biệt.
Cho f(x) là hàm số liên tục trên tập số thực \(\mathbb{R}\) và thỏa mãn \(f\left(x^{2}+3 x+1\right)=x+2 .\) Tính \(I=\int\limits_{1}^{5} f(x) d x\)
\(\begin{array}{l} f\left(x^{2}+3 x+1\right)=x+2 \\ \Rightarrow f\left(x^{2}+3 x+1\right)(2 x+3)=(x+2)(2 x+3) \\ \Rightarrow \int\limits_{0}^{1} f\left(x^{2}+3 x+1\right)(2 x+3) d x=\int\limits_{0}^{1}(x+2)(2 x+3) d x \\ \Rightarrow \int\limits_{0}^{1} f\left(x^{2}+3 x+1\right)(2 x+3) d x=\frac{61}{6} \end{array}\)
Đặt \(t=x^{2}+3 x+1 \Rightarrow d t=(2 x+3) d x\)
Đổi cận \(\left\{\begin{array}{l} x=0 \Rightarrow t=1 \\ x=1 \Rightarrow t=5 \end{array}\right.\)
\(\begin{array}{l} \Rightarrow \int\limits_{0}^{1} f\left(x^{2}+3 x+1\right)(2 x+3) d x=\int\limits_{1}^{5} f(t) d t=\int\limits_{1}^{5} f(x) d x \\ \text { Vậy } \int\limits_{1}^{5} f(x) d x=\frac{61}{6} \end{array}\)
Có bao nhiêu giá trị nguyên của m hàm số \(y=\left|x^{3}-m x^{2}+12 x+2 m\right|\) luôn đồng biến trên khoảng \((1 ;+\infty) ?\)
Xét hàm số \(g(x)=x^{3}-m x^{2}+12 x+2 m\) có
\(g'(x)=3x^{2}-2m x+12, g(1)=m+13\)
Để hàm số \(y=\left|x^{3}-m x^{2}+12 x+2 m\right|\) đồng biến trên \((1 ;+\infty) \) thì ta xét hai trường hợp
TH1: Hàm số g(x) đồng biến trên \((1 ;+\infty) \) và \(g(1)\ge0\)
\(\Leftrightarrow\left\{\begin{array}{l} 3 x^{2}-2 m x+12 \geqslant 0\forall x>1 \\ m+13 \geqslant 0 \end{array}\right.\)
\(\Leftrightarrow \left\{\begin{array}{l} m \leqslant \frac{3 x^{3}+12}{2 x}\forall x\ge 1\,\,\,\, (1)\\ m \geq-13 \end{array}\right.\)
Xét (1):
Đặt \(h(x)=\frac{3 x^{2}+12}{2 x} \,\,có\,\,h'(x)=\frac{3 x^{2}-12}{2 x^{2}}\)
\(\begin{array}{l} h^{\prime}(x)=0 \Leftrightarrow\left[\begin{array}{l} x=2 \\ x=-2 \notin(1 ;+\infty) \end{array}\right. \\ h(1)=\frac{15}{2}, h(2)=6 \\ \Rightarrow \min\limits _{(1,+\infty)}h(x)=6 \end{array}\)
Vậy \((1) \Leftrightarrow m\le \min\limits_{(1 ;+\infty)} h(x)=6\)
Kết hợp với \(m\ge -13\) và m nguyên ta có \(m \in\{-13,-12,..., 5 ; 6\}\)
Vậy có 20 giá trị nguyên m thỏa mãn.
TH2: Hàm số g(x) nghịch biến trên \((1 ;+\infty) \) và \(g(1)\le0\)
Điều này không xảy ra vì \(\lim\limits _{x \rightarrow+\infty}\left(3 x^{2}-2 m12\right)=+\infty\)
Vậy có 20 giá trị m thỏa mãn yêu cầu bài toán
Cho phương trình\(\log _{2}^{2} x-(5 m+1) \log _{2} x+4 m^{2}+m=0 .\) Biết phương trình có 2 nghiệm phân biệt \(x_{1}, x_{2}\) thỏa mãn\(x_{1}+x_{2}=165 .\) Giá trị của \(\left|x_{1}-x_{2}\right|\) bằng:
ĐK: x>0
Đặt \(t=\log _{2} x\) khi đó phương trình trở thành \(t^{2}-(5 m+1) t+4 m^{2}+m=0(*)\)
Để phương trình ban đầu có 2 nghiệm phân biệt thì phương trình (*) cũng phải có 2 nghiệm phân biệt
\(\begin{array}{l}
\Rightarrow \Delta>0 \\
\Rightarrow(5 m+1)^{2}-4\left(4 m^{2}+m\right)>0 \\
\Leftrightarrow 25 m^{2}+10 m+1-16 m^{2}-4 m>0 \\
\Leftrightarrow 9 m^{2}+6 m+1>0 \\
\Leftrightarrow(3 m+1)^{2}>0 \\
\Leftrightarrow m \neq-\frac{1}{3}
\end{array}\)
Khi đó phương trình (*) có hai nghiệm phân biệt \(\left[\begin{array}{l} t_{1}=\frac{5 m+1+3 m+1}{2}=4 m+1 \\ t_{2}=\frac{5 m+1-3 m-1}{2}=m \end{array} \Rightarrow\left[\begin{array}{l} x_{1}=2^{4 m+1} \\ x_{2}=2^{m} \end{array}\right.\right.\)
Theo đề bài ta có: \(x_{1}+x_{2}=165 \Leftrightarrow 2^{4 m+1}+2^{m}=165 \Leftrightarrow 2 \cdot\left(2^{m}\right)^{4}+2^{m}=165\)
Đặt \(u=2^{m}>0\) phương trình trở thành \(2 u^{4}+u-165=0\)
\(\begin{array}{l} \Leftrightarrow(u-3)\left(2 u^{3}+6 u^{2}+18 u+55\right)=0 \\ \Leftrightarrow u=3\left(\text { Do } u>0 \Rightarrow 2 u^{3}+6 u^{2}+18 u+55>0\right) \\ \Rightarrow 2^{m}=3 \\ \Rightarrow x_{1}=2 \cdot\left(2^{m}\right)^{4}=162, x_{2}=2^{m}=3 \end{array}\)
Vậy \(\left|x_{1}-x_{2}\right|=162-3 \mid=159\)
Cho y=f(x) là hàm đa thức bậc 4 và có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-12 ; 12] để hàm số \(g(x)=|2 f(x-1)+m \mid\) có 5 điểm cực tri?
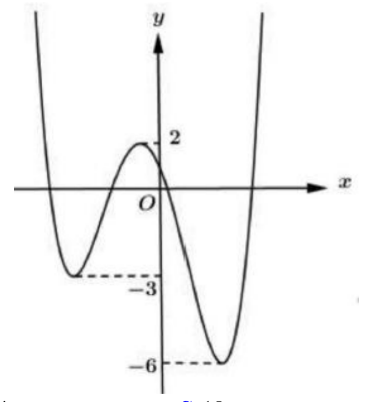
Đặt \(t=x-1\) khi đó ta có \(y=g(t+1)=12 f(t)+m \mid=\sqrt{(2 f(t)+m)^{2}}\)
\(\begin{array}{l} \Rightarrow y^{\prime}=\frac{2(2 f(t)+m) \cdot 2 f^{\prime}(t)}{2 \sqrt{(2 f(t)+m)^{2}}}=\frac{2[2 f(t)+m] f^{\prime}(t)}{\sqrt{(2 f(t)+m)^{2}}} \\ y^{\prime}=0 \Leftrightarrow\left[\begin{array}{l} 2 f(t)+m=0 \\ f^{\prime}(t)=0 \end{array}\right. \end{array}\)
Đề hàm số \(y=g(t+1)=|2 f(t)+m|\) có 5 điểm cực trị thì phương trình \(y^{\prime}=0\) phai có 5 nghiệm bội lè phân biệt.
Dựa vào đồ thị hàm số ta thấy phương trình \(f^{\prime}(t)=0\) có 3 nghiệm đơn phân biệt \(\Rightarrow \) phương trình \(2 f(t)+m=0 \Leftrightarrow f(t)=-\frac{m}{2}\) phải có 2 nghiệm bội lẻ phân biệt.
\(\Rightarrow\) Đương thẳng \(y=-\frac{m}{2}\) cắt đồ thị hàm số y=f(t) tai 2 điểm phân biệt.
\(\Leftrightarrow\left[\begin{array}{l} -6<-\frac{m}{2} \leq-3 \\ -\frac{m}{2} \geq 2 \end{array} \Leftrightarrow\left[\begin{array}{l} 3 \leq \frac{m}{2}<6 \\ \frac{m}{2} \leq-2 \end{array} \Leftrightarrow\left[\begin{array}{l} 6 \leq m<12 \\ m \leq-4 \end{array}\right.\right.\right.\)
Kết hợp điều kiện \([-12 ; 12] \Rightarrow m \in[-12 ;-4] \cup[6 ; 12)\)
Mà \(n \in \mathbb{Z} \Rightarrow m \in\{-12 ;-11 ; \ldots ;-4 ; 6 ; 7 ; \ldots ; 11\}\)
Vậy có 15 giá trị m thỏa mãn yêu cầu bài toán.
Cho hai số thục dương x, y thỏa mãn \(\log _{2} x+x(x+y)=\log _{2}(6-y)+6 x\). Giá trị nhỏ nhất của biểu thức \(T=x^{3}+3 y\) là:
ĐKXĐ: \(\left\{\begin{array}{l} x>0 \\ 6-y>0 \end{array} \Leftrightarrow\left\{\begin{array}{l} x>0 \\ y<6 \end{array}\right.\right.\)
Ta có
\(\begin{aligned} & \log _{2} x+x(x+y)=\log _{2}(6-y)+6 x \\ \Leftrightarrow & \log _{2} x+x^{2}+x y=\log _{2}(6-y)+6 x \\ \Leftrightarrow & \log _{2} x+x^{2}=\log _{2}(6-y)+6 x-x y \\ \Leftrightarrow & \log _{2} x+x^{2}=\log _{2}(6-y)+x(6-y) \\ \Leftrightarrow & 2 \log _{2} x+x^{2}=\log _{2}(6-y)+\log _{2} x+x(6-y) \\ \Leftrightarrow & \log _{2} x^{2}+x^{2}=\log _{2}[x(6-y)]+x(6-y) \end{aligned}\)
Xét hàm đặc trưng \(f(t)=\log _{2} t+t(t>0) \text { ta có } f^{\prime}(t)=\frac{1}{t \ln 2}+1>0 \forall t>0\)
\(\Rightarrow\) hàm số đồng biến trên \((0 ;+\infty)\)
Do đó từ \(f\left(x^{2}\right)=f(x(6-y)) \Leftrightarrow x^{2}=x(6-y) \Leftrightarrow x=6-y(\text { Do } x>0) \Leftrightarrow y=6-x\)
Khi đó ta có \(T=x^{3}+3 y=x^{3}+3(6-x)=x^{3}-3 x+18 \text { với } x>0\)
Ta có \(T^{\prime}=3 x^{2}-3=0 \Leftrightarrow x=\pm 1\)
BBT:
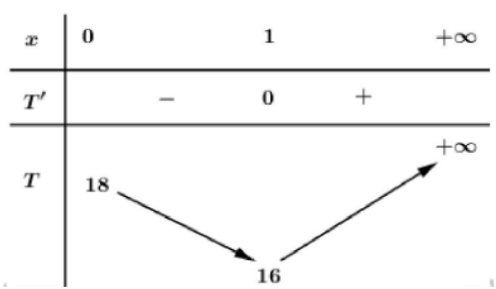
Dựa bào bảng biến thiên ta có \(T_{\min }=T(1)=16\)
Cho hình lăng trụ \(A B C . A^{\prime} B^{\prime} C^{\prime}\) có đáy ABC là tam giác vuông tại A . Cạnh BC=2a và \(\widehat{ A B C}=60^{\circ}\) .Biết tứ giác \(B C C^{\prime} B^{\prime}\) là hinh thoi có \(\widehat{ B^{\prime} B C}\) nhon. Măt phăng \(\left(B C C^{\prime} B^{\prime}\right)\) vuông góc vói (A B C) và măt phẳng \(\left(A B B^{\prime} A^{\prime}\right)\) tạo với (A B C) góc \(45^{\circ} .\) Thể tích khối lăng trụ \(A B C . A^{\prime} B^{\prime} C^{\prime}\) bằng:
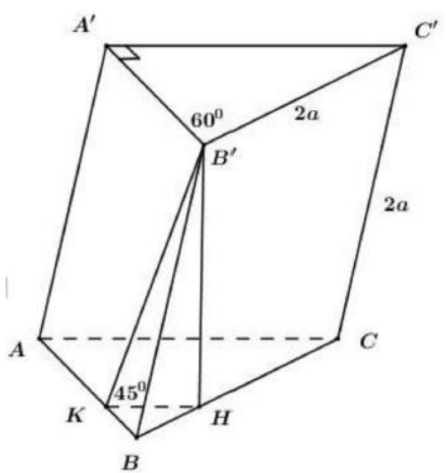
Trong\(\left.\left(B C C^{\prime} B^{\prime}\right) \text { kẻ } B^{\prime} H \perp B C(H \in B C) \text { (do } \widehat{ B^{\prime} B C} \text { nhon }\right)\)
Trong (ABC) kẻ HK//AC \(\Rightarrow H K \perp A B \)
\(\text { ta có: }\left\{\begin{array}{l} A B \perp H K \\ A B \perp B H \end{array} \Rightarrow A B \perp\left(B^{\prime} H K\right) \Rightarrow A B \perp B K\right.\)
Ta có \(\left\{\begin{array}{l} \left(A B B^{\prime} A^{\prime}\right) \cap(A B C)=A B \\ \left.B^{\prime} K \subset\left(A B B^{\prime} A^{\prime}\right), B^{\prime} K \perp A B \Rightarrow \widehat{\left(A B B^{\prime} A^{\prime}\right) ;(A B C)}\right)=\widehat{(B K ; H K)}=\widehat{ B^{\prime} H K}=45^{\circ} \\ H K \subset(A B C), H K \perp A B \end{array}\right.\)
\(\Rightarrow \triangle B^{\prime} H K \text { vuông cân tai } H \Rightarrow B^{\prime} H=H K=x\)
Xét tam giác BB'H ta có \(B H=\sqrt{B B^{2}-B H^{\prime 2}}=\sqrt{4 a^{2}-x^{2}}\)
Xét tam giác vuông ABC có \(4 C=B C \cdot \sin 60^{\circ}=a \sqrt{3}, A B=B C \cdot \cos 60^{\circ}=a\)
Áp dụng định lí Ta - lét \(\frac{B H}{B C}=\frac{H K}{A C} \Rightarrow \frac{\sqrt{4 a^{2}-x^{2}}}{2 a}=\frac{x}{a \sqrt{3}}\)
\(\begin{array}{l} \Leftrightarrow 3\left(4 a^{2}-x^{2}\right)=4 x^{2} \\ \Leftrightarrow 12 a^{2}-3 x^{2}=4 x^{2} \\ \Leftrightarrow x^{2}=\frac{12 a^{2}}{7} \\ \Leftrightarrow x=\frac{2 a \sqrt{21}}{7}=B^{\prime} H \\ S_{\Delta B C}=\frac{1}{2} A B \cdot A C=\frac{1}{2} \cdot a \cdot a \sqrt{3}=\frac{a^{2} \sqrt{3}}{2} \end{array}\)
Vậy \(V_{A B C, A \mathrm{BC}}=B H S_{\mathrm{A} A B C}=\frac{2 a \sqrt{21}}{7} \cdot \frac{a^{2} \sqrt{3}}{2}=\frac{3 a^{3} \sqrt{7}}{7}\)




