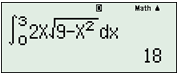Trong không gian Oxyz, cho đường thẳng \(d:\frac{x+1}{1}=\frac{z-1}{-1}=\frac{y-3}{2}\). Một vectơ chỉ phương của d là

Trong không gian Oxyz, cho mặt phẳng \(\left( P \right):x - 2y + 2z - 1 = 0\). Khoảng cách từ điểm \(A\left( {1; - 2;1} \right)\) đến mặt phẳng (P) bằng

Tìm các giá trị của tham số m để hàm số \(y = \frac{1}{2}\ln \left( {{x^2} + 4} \right) - mx + 3\) nghịch biến trên khoảng \(\left( { - \infty ; + \infty } \right)\).

Trong không gian Oxyz cho điểm M(1;1;1). Mặt phẳng (P) đi qua M và cắt chiều dương của các trục Ox,Oy,Oz lần lượt tại các điểm \(A\left( {a;0;0} \right),B\left( {0;b;0} \right),C\left( {0;0;c} \right)\) thỏa mãn OA = 2OB và thể tích khối tứ diện OABC đạt giá trị nhỏ nhất. Tính S = 2a + b + 3c.

Cho a, b, x là các số thực dương thỏa mãn \({\log _5}x = 2{\log _{\sqrt 5 }}a + 3{\log _{\frac{1}{5}}}b\). Mệnh đề nào là đúng?

Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình chữ nhật \(AB=a,AD=a\sqrt{2},SA\bot \left( ABCD \right)\) và SA=a (tham khảo hình vẽ). Khoảng cách từ A đến mặt phẳng \(\left( SBD \right)\) bằng:

Nghiệm của phương trình 2^x-3 = \(\frac12\) là

Cho không gian Oxyz, cho điểm A(0;1;2) và hai đường thẳng \({d_1}:\left\{ \begin{array}{l} x = 1 + t\\ y = - 1 - 2t\\ z = 2 + t \end{array} \right.\), \({d_2}:\frac{x}{2} = \frac{{y - 1}}{1} = \frac{{z + 1}}{{ - 1}}\). Viết phương trình mặt phẳng \(\left( \alpha  \right)\) đi qua A và song song với hai đường thẳng \({d_1},{d_2}\).

Trong không gian Oxyz, cho đường thẳng \(d:\frac{x}{2} = \frac{{y - 3}}{1} = \frac{{z - 2}}{{ - 3}}\) và mặt phẳng \(\left( P \right):x - y + 2z - 6 = 0\). Đường thẳng nằm trong mặt phẳng \(\left( P \right)\), cắt và vuông góc với đường thẳng d có phương trình là

Trong không gian Oxyz, mặt cầu có tâm I(2;-1;1) và tiếp xúc mặt phẳng (Oyz) có phương trình là:

Biết \(F\left( x \right)\) là một nguyên hàm của hàm số \(f\left( x \right) = {x^2} + x\) và \(F\left( 1 \right) = 1\). Giá trị của \(F\left( { - 1} \right)\) bằng

Cho hai hàm số f(x) và g(x) có đạo hàm trên đoạn [1;4] và thỏa mãn hệ thức \(\left\{ \begin{array}{l} f\left( 1 \right) + g\left( 1 \right) = 4\\ g\left( x \right) = - x.f'\left( x \right);\,\,\,\,\,f\left( x \right) = - x.g'\left( x \right) \end{array} \right.\). Tính \(I = \int\limits_1^4 {\left[ {f\left( x \right) + g\left( x \right)} \right]{\rm{d}}x} \).

Nguyên hàm của hàm số \(y = \frac{1}{{1 - x}}\) là:

Tìm số giá trị nguyên thuộc đoạn \(\left[ { - 2021\,;2021} \right]\) của tham số m để đồ thị hàm số \(y = \frac{{\sqrt {x - 3} }}{{{x^2} + x - m}}\) có đúng hai đường tiệm cận.

Tiệm cận đứng của đồ thị hàm số \(y = \frac{{x - 1}}{{x + 1}}\) là