Đề minh họa THPT QG môn Vật Lý năm 2018 - Bộ GD&ĐT
Đề minh họa THPT QG môn Vật Lý năm 2018
-
Hocon247
-
40 câu hỏi
-
90 phút
-
36 lượt thi
-
Dễ
Tham gia [ Hs Hocon247.com ] - Cộng Đồng Luyện Thi Trực Tuyến để được học tập những kiến thức bổ ích từ HocOn247.com
Một vật dao động điều hòa trên trục Ox quanh vị trí cân bằng O. Gọi \(A,{\rm{ }}\omega \) và \(\varphi \) lần lượt là biên độ, tần số góc và pha ban đầu của dao động. Biểu thức li độ của vật theo thời gian t là
Biểu thức li độ của vật theo thời gian là : \({\rm{ x = Acos(}}\omega {\rm{t + }}\varphi {\rm{)}}\)
Dao động cơ tắt dần
Dao động tắt dần có biên độ giảm dần theo thời gian
Trong sóng cơ, công thức liên hệ giữa tốc độ truyền sóng v, bước sóng \(\lambda \) chu kì T của sóng là
Trong sóng cơ, công thức liên hệ giữa tốc độ truyền sóng v, bước sóng \(\lambda \) chu kì T của sóng là \(\lambda {\rm{ = }}vT\)
Khi đặt điện áp \(u = {\rm{ 220}}\sqrt 2 cos100t\pi t\left( V \right)\) (t tính bằng s) vào hai đầu một điện trở thì tần số góc của dòng điện chạy qua điện trở này là
Tần số góc của dòng điện chạy qua điện trở là: \({\rm{100}}\pi {\rm{ rad/s}}{\rm{. }}\)
Nguyên tắc hoạt động của máy phát điện xoay chiều dựa trên hiện tượng
Nguyên tắc hoạt động của máy phát điện xoay chiều dựa trên hiện tượng cảm ứng điện từ
Trong thông tin liên lạc bằng sóng vô tuyến, mạch khuếch đại có tác dụng
Trong thông tin liên lạc bằng sóng vô tuyến, mạch khuếch đại có tác dụng tăng cường độ của tín hiệu.
Chất nào sau đây phát ra quang phổ vạch phát xạ?
Chất khí nóng sáng ở áp suất thấp phát ra quang phổ vạch phát xạ
Khi chiếu một chùm tia tử ngoại vào một ống nghiệm đựng dung dịch fluorexêin thì thấy dung dịch này phát ra ánh sáng màu lục. Đây là hiện tượng
Khi chiếu một chùm tia tử ngoại vào một ống nghiệm đựng dung dịch fluorexêin thì thấy dung dịch này phát ra ánh sáng màu lục. Đây là hiện tượng quang - phát quang.
Số prôtôn có trong hạt nhân \({}_{84{\rm{ }}}^{210}Po\) là
Số prôtôn có trong hạt nhân \({}_{84{\rm{ }}}^{210}Po\) là 84
Phản ứng hạt nhân nào sau đây là phản ứng nhiệt hạch?
\({}_1^2H + {}_1^3H \to {}_2^4He + {}_0^1n\) là phản ứng nhiệt hạch
Một điện tích điểm q dịch chuyển từ điểm M đến điểm N trong điện trường, hiệu điện thế giữa hai điểm là \({U_{MN}}\). Công của lực điện thực hiện khi điện tích q dịch chuyển từ M đến N là
Công của lực điện thực hiện khi điện tích q dịch chuyển từ M đến N là \({\rm{A = q}}{{\rm{U}}_{{\rm{MN}}}}\)
Phát biểu nào sau đây đúng? Trong từ trường, cảm ứng từ tại một điểm
Trong từ trường, cảm ứng từ tại một điểm ngược hướng với đường sức từ
Một con lắc lò xo gồm lò xo có độ cứng k, vật nhỏ khối lượng 100g, dao động điều hòa với tần số góc 20 rad/s. Giá trị của k là
Giá trị độ cứng k của lò xo được xác định bởi biểu thức \(k = {\omega ^2}m = {20^2}.0,1 = 40N/m\)
Giao thoa ở mặt nước được tạo bởi hai nguồn sóng kết hợp dao động điều hòa cùng pha theo phương thẳng đứng tại hai vị trí S1 và S2. Sóng truyền trên mặt nước có bước sóng 6 cm. Trên đoạn thẳng S1S2 hai điểm gần nhau nhất mà phần tử nước tại đó dao động với biên độ cực đại cách nhau
Bước sóng \(\lambda = 6cm\)
Trên đoạn thẳng nối hai nguồn, hai điểm gần nhau nhất mà phần tử nước tại đó dao động với biên độ cực đại cách nhau 1 khoảng bằng \(\lambda /2{\rm{ }} = {\rm{ }}3cm\)
Đặt điện áp xoay chiều vào hai đầu đoạn mạch gồm điện trở R và cuộn cảm thuần mắc nối tiếp. Khi đó, cảm kháng của cuộn cảm có giá trị bằng R. Hệ số công suất của đoạn mạch là
Cảm kháng: \({Z_L} = {\rm{ }}R\)
Hệ số công suất của đoạn mạch \(cos\varphi = \frac{R}{Z} = \frac{R}{{\sqrt {{R^2} + Z_L^2} }} = \frac{R}{{\sqrt {{R^2} + {R^2}} }} = \frac{1}{{\sqrt 2 }} = 0,71\)
Trong thí nghiệm Y-âng về giao thoa ánh sáng, khoảng cách giữa hai khe là 0,5mm, khoảng cách từ mặt phẳng chứa hai khe đến màn quan sát là 2m. Chiếu sáng các khe bằng bức xạ có bước sóng 500 nm. Trên màn, khoảng cách giữa hai vân sáng liên tiếp là
Khoảng cách giữa hai vân sáng liên tiếp: \(i = \frac{{\lambda D}}{a} = 2mm\)
Một chất bán dẫn có giới hạn quang dẫn là \(4,97{\rm{ }}\mu m.\) Lấy \(h = 6,{625.10^{ - 34}}J.s;\,\,\,c = {3.10^8}m/s\) và \(e = 1,{6.10^{ - 19}}{\rm{ }}C.\) Năng lượng kích hoạt (năng lượng cần thiết để giải phóng một êlectron liên kết thành êlectron dẫn) của chất đó là
Năng lượng kích hoạt của chất đó: \(E = \frac{{hc}}{{{\lambda _0}}} = \frac{{6,{{625.10}^{ - 34}}{{.3.10}^8}}}{{4,{{97.10}^{ - 6}}}} = 0,25eV\)
Giả sử hai hạt nhân X và Y có độ hụt khối bằng nhau, nếu số nuclôn của hạt nhân X lớn hơn số nuclôn của hạt nhân Y thì
Ta có:
\(\left\{ \begin{array}{l}
\Delta {m_X} = \Delta {m_Y}\\
{A_X} > {A_Y}
\end{array} \right. \Rightarrow \left\{ \begin{array}{l}
{{\rm{W}}_{lkX}} = {{\rm{W}}_{lkY}}\\
\frac{{{{\rm{W}}_{lkX}}}}{{{A_X}}} = \frac{{{{\rm{W}}_{lkY}}}}{{{A_Y}}}
\end{array} \right. \Leftrightarrow {\varepsilon _X} > {\varepsilon _Y}\)
=> Hạt nhân Y bền vững hơn hạt nhân X
Một khung dây phẳng diện tích 20cm2 đặt trong từ trường đều có vectơ cảm ứng từ hợp với vectơ pháp tuyến của mặt phẳng khung dây một góc 600 và có độ lớn 0,12T. Từ thông qua khung dây này là
Từ thông qua khung dây: \(\phi = BS.cos\alpha = 0,{12.20.10^{ - 4}}.cos60 = 1,{2.10^{ - 4}}{\rm{W}}b\)
Tốc độ của ánh sáng trong chân không là \(c = {3.10^8}{\rm{ }}m/s.\) Nước có chiết suất n=1,33 đối với ánh sáng đơn sắc màu vàng. Tốc độ của ánh sáng màu vàng trong nước là
Tốc độ của ánh sáng màu vàng trong nước: \(v = \frac{c}{n} = \frac{{{{3.10}^8}}}{{1,33}} = 2,{26.10^5}\left( {km/s} \right)\)
Một sợi dây dài 2m với hai đầu cố định, đang có sóng dừng. Sóng truyền trên dây với tốc độ 20 m/s. Biết rằng tần số của sóng truyền trên dây có giá trị trong khoảng từ 11Hz đến 19Hz. Tính cả hai đầu dây, số nút sóng trên dây là
Ta có điều kiện sóng dừng trên hai đầu dây cố định: \(l = k\frac{\lambda }{2} = k\frac{v}{{2f}} \to f = k\frac{v}{{2l}}\)
Mặt khác:
\(\begin{array}{l}
11Hz < f < 19Hz \to 11 < k\frac{v}{{2l}} < 2,2 \to 11 < k < 3,8\\
\to k = 3
\end{array}\)
Số nút sóng \(= {\rm{ }}k + 1 = 4\) nút
Cường độ dòng điện trong một mạch dao động LC lí tưởng có phương trình \(i = 2cos\left( {{{2.10}^7}t{\rm{ }} + \pi /2} \right){\rm{ }}\left( {mA} \right)\) (t tính bằng s). Điện tích của một bản tụ điện ở thời điểm \(\pi /20{\rm{ }}\left( {\mu s} \right)\) có độ lớn là
Ta có \({\left( {\frac{i}{{{I_0}}}} \right)^2} = {\left( {\frac{q}{{{Q_0}}}} \right)^2} = 1\)
Tại \(t = \frac{\pi }{{20}}\mu s:\) thay vào phương trình i, ta có
\(i = 0A \Rightarrow q = {Q_0}q = {Q_0} = \frac{{{I_0}}}{\omega } = \frac{{{{2.10}^{ - 3}}}}{{{{2.10}^7}}} = {10^{ - 7}}C = 0,1\mu C\)
Trong ống Cu-lít-giơ (ống tia X), hiệu điện thế giữa anôt và catôt là 3kV. Biết động năng cực đại của êlectron đến anôt lớn gấp 2018 lần động năng cực đại của êlectron khi bứt ra từ catôt. Lấy \(e = 1,{6.10^{ - 19}}{\rm{ }}C;{\rm{ }}{m_e} = 9,{1.10^{ - 31}}{\rm{ }}kg.\) Tốc độ cực đại của êlectron khi bứt ra từ catôt là
Ta có: \(e{U_h} = {{\rm{W}}_{d\max 1}}\) (Động năng cực đại của electron đến anot)
Goi \({W_{dmax2}}\) là động năng cực đại của electron khi bứt ra từ catốt.
Ta có \({W_{dmax1}} = 2018{W_{dmax2}}\)
\(\begin{array}{l}
{W_{dmax2}} = \frac{{{W_{dmax1}}}}{{2018}} = \frac{{e{U_h}}}{{2018}} = \frac{{1,{{6.10}^{ - 19}}{{.3.10}^3}}}{{2018}} = \frac{{m{v^2}}}{2}\\
\to v = {\rm{723026}}m/s \approx 723km/s
\end{array}\)
Xét nguyên tử hiđrô theo mẫu nguyên tử Bo. Lấy \({r_0} = 5,{3.10^{-11}}{\rm{ }}m;{\rm{ }}{m_e} = 9,{1.10^{-31}}{\rm{ }}kg;{\rm{ }}k = {9.10^9}{\rm{ }}N.{m^2}/{C^2}\) và \(e = 1,{6.10^{-19}}{\rm{ }}C\). Khi chuyển động trên quỹ đạo dừng M, quãng đường mà êlectron đi được trong thời gian 10-8s là
Ta có: Lực điện đóng vai trò là lực hướng tâm \(k\frac{{{e^2}}}{{r_n^2}} = m\frac{{v_n^2}}{{r_n^{}}} \to {v_n} = e\sqrt {\frac{k}{{{r_n}m}}} = \frac{e}{n}\sqrt {\frac{k}{{{r_0}m}}} \)
Tốc độ góc \(\omega = \frac{{{v_n}}}{{{r_n}}}\)
Khi chuyển động trên quỹ đạo dừng M: n=3
\(\begin{array}{l}
{v_M} = \frac{e}{3}\sqrt {\frac{k}{{{r_0}m}}} = {\rm{738553, 34 }}m/s\\
\to \omega = \frac{{{v_M}}}{{{r_M}}} = 1,{53.10^{15}}rad/s
\end{array}\)
Góc quyét của electron trong khoảng thời gian 10-8s là: \(\Delta \varphi = \omega \Delta t = 15,{3.10^6}\)
Quãng đường mà electron đi được trong thời gian 10-8s là:
\(S = {r_M}.\Delta \varphi = 9.{r_0}\Delta \varphi = 7,{29.10^{ - 3}} = 7,29mm\)
Hai điện tích điểm \({q_1} = {10^{ - 8}}{\rm{ }}C\) và \({q_2} = - {\rm{ }}{3.10^{ - 8}}{\rm{ }}C\) đặt trong không khí tại hai điểm A và B cách nhau 8 cm. Đặt điện tích điểm \(q = {10^{ - 8{\rm{ }}}}C\) tại điểm M trên đường trung trực của đoạn thẳng AB và cách AB một khoảng 3cm. Lấy \(k = {9.10^9}{\rm{ }}N.{m^2}/{C^2}.\) Lực điện tổng hợp do q1 và q2 tác dụng lên q có độ lớn là
Gọi H - trung điểm \({\rm{AB = > MH = 3cm, AH = HB = 4cm, AM = BM = 5cm}}\)
Gọi F1 là lực điện do q1 tác động lên q: \({F_1} = k\frac{{\left| {{q_1}q} \right|}}{{A{M^2}}} = 3,{6.10^{ - 4}}N\)
F2 là lực điện do q2 tác động lên q: \({F_2} = k\frac{{\left| {{q_2}q} \right|}}{{A{M^2}}} = 1,{08.10^{ - 3}}N\)
Lực điện tổng hợp do q1 và q2 tác dụng lên q là \(\overrightarrow F = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} \)
Gọi góc tạo bởi hai véctơ \(\overrightarrow {{F_1}} ,\,\overrightarrow {{F_2}} \) là \(\pi - \alpha \)
Ta có \(\alpha = 2\widehat {HMB}\)
Mặt khác \(cos\widehat {HMB} = \frac{{MH}}{{BM}} = \frac{3}{5} \to \widehat {HMB} = 53,1^\circ \to \alpha = 106,26^\circ \)
Ta có
\({F^2} = F_1^2 + F_2^2 + 2{F_1}{F_2}cos\alpha = {\left( {3,{{6.10}^{ - 4}}} \right)^2} + {\left( {1,{{08.10}^{ - 3}}} \right)^2} + 2.3,{6.10^{ - 4}}.1,{08.10^{ - 3}}.cos73,39^\circ \to F = 1,{23.10^{ - 3}}N\)
Cho mạch điện có sơ đồ như hình bên:
\(E = 12{\rm{ }}V;{\rm{ }}{R_1} = 4{\rm{ }}\Omega ;{\rm{ }}{R_2} = {R_3} = 10{\rm{ }}\Omega .\) Bỏ qua điện trở của ampe kế A và dây nối. Số chỉ của ampe kế là 0,6 A. Giá trị điện trở trong r của nguồn điện là
Từ sơ đồ mạch điện ta có \(\left( {R3//R2} \right){\rm{ }}ntR1\)
Hiệu điện thế của U3 là : \({U_3} = {I_A}.{R_3} = 0,6.10 = 6V\)
Do \({R_3}//{\rm{ }}{R_2}\) nên ta có \({U_{2{\rm{ }}}} = {U_3} = {\rm{ }}6V\)
Cường độ dòng điện qua R2 là \({I_2} = \frac{{{U_2}}}{{{R_2}}} = \frac{6}{{10}} = 0,6V\)
Cường độ dòng điện chạy trong mạch là \(I = {I_1} + {I_2} = 0,6 + 0,6 = 1,2A\)
Điện trở toàn mạch là \({R_h} = {R_1} + \frac{{{R_2}.{R_3}}}{{{R_2} + {R_3}}} = 4 + \frac{{10.10}}{{10 + 10}} = 9\Omega \)
Áp dụng định luật Ohm cho toàn mạch ta có \(I = \frac{\xi }{{r + {R_b}}} \Rightarrow 1,2 = \frac{{12}}{{r + 9}} \Rightarrow r = 1\Omega \)
Trong giờ thực hành, để đo tiêu cự f của một thấu kính hội tụ, một học sinh dùng một vật sáng phẳng nhỏ AB và một màn ảnh. Đặt vật sáng song song với màn và cách màn ảnh một khoảng 90cm. Dịch chuyển thấu kính dọc trục chính trong khoảng giữa vật và màn thì thấy có hai vị trí thấu kính cho ảnh rõ nét của vật trên màn, hai vị trí này cách nhau một khoảng 30 cm. Giá trị của f là
Từ công thức thấu kính \(\frac{1}{f} = \frac{1}{d} + \frac{1}{{d'}}\)
Ta thấy công thức có tính đối xứng đối với d và d’ nghĩa là, nếu ta hoán vị d và d’ thì công thức không có gì thay đổi; nói cách khác, khi vật cách thấu kính là d thì ảnh cách thấu kính là d’, ngược lại, nếu vật cách thấu kính là d’thì ảnh sẽ cách thấu kính là D. Vậy ở hình vẽ trên, với O1và O2 là hai vị trí của thấu kính để cho ảnh rõ nét trên màn ta có : \({d_1} = d{_2};{\rm{ }}d{_1} = {d_2}\)
Vậy ta có
\(\begin{array}{l}
d{_1} + {d_1}{\rm{ = D;}}d{_1} - {d_1}{\rm{ = }}l \Rightarrow d{_1} = \frac{{D + l}}{2};{d_1} = \frac{{D - l}}{2}\\
\Rightarrow \frac{1}{f} = \frac{1}{{d'}} + \frac{1}{d} = \frac{{4D}}{{{D^2} - {l^2}}} \Rightarrow f = \frac{{{D^2} - {l^2}}}{{4D}} = \frac{{{{90}^2} - {{30}^2}}}{{4.90}} = 20cm
\end{array}\)
Cho mạch điện có sơ đồ như hình bên:
L là một ống dây dẫn hình trụ dài 10 cm, gồm 1000 vòng dây, không có lõi, được đặt trong không khí; điện trở R; nguồn điện có E=12V và \(r = 1\Omega .\) Biết đường kính của mỗi vòng dây rất nhỏ so với chiều dài của ống dây. Bỏ qua điện trở của ống dây và dây nối. Khi dòng điện trong mạch ổn định thì cảm ứng từ trong ống dây có độ lớn là \(2,{51.10^{ - 2}}{\rm{ }}T.\) Giá trị của R là
Từ công thức tính cảm ứng từ do dòng điện chạy trong ống dây gây ra ta có
\(B = 4\pi {.10^{ - 7}}nI \Rightarrow I = \frac{B}{{4\pi {{.10}^{ - 7}}n}} = \frac{{2,{{51.10}^{ - 2}}}}{{4\pi {{.10}^{ - 7}},{{10}^4}}} = 2A\)
Áp dụng định luật Ohm cho toàn mạch ta có \(I = \frac{\xi }{{r + R}} = \frac{{12}}{{1 + R}} = 2 \Rightarrow R = 5\Omega \)
Hai con lắc lò xo giống hệt nhau được treo vào hai điểm ở cùng độ cao, cách nhau 3cm
Kích thích cho hai con lắc dao động điều hòa theo phương thẳng đứng với phương trình lần lượt \({x_1} = 3cos\omega t\) và \({x_2} = 6cos\left( {\omega t + \pi /3} \right){\rm{ }}\left( {cm} \right).\) Trong quá trình dao động, khoảng cách lớn nhất giữa hai vật nhỏ của các con lắc bằng
Ta có: Khoảng cách giữa hai vật nhỏ của con lắc bằng: \(d = \sqrt {{3^2} + {{\left| {{x_1} - {x_2}} \right|}^2}} \)
Ta có: \({x_1} - {x_2} = 3co{\rm{s}}\left( {\omega t} \right) - 6co{\rm{s}}\left( {\omega t + \frac{\pi }{3}} \right) = 3co{\rm{s}}\left( {\omega t} \right) + 6co{\rm{s}}\left( {\omega t + \frac{\pi }{3} + \pi } \right)\)
Biên độ tổng hợp: của \({x_1} - {x_2}\) là \({A^2} = {3^2} + {6^2} + 2.3.6.co{\rm{s}}\left( {\pi + \frac{\pi }{3}} \right) \to A = 5,2cm\)
\({d_{max}} \leftrightarrow {\left| {{x_1} - {x_2}} \right|_{max}} = A \to {d_{max}} = \sqrt {{3^2} + {{\left( {5.2} \right)}^2}} = 6cm\)
Một con lắc lò xo có m=100g và k=12,5 N/m Thời điểm ban đầu (t=0) lò xo không biến dạng, thả nhẹ để hệ vật và lò xo rơi tự do sao cho trục lò xo luôn có phương thẳng đứng và vật nặng ở phía dưới lò xo. Đến thời điểm \({t_1} = 0,11{\rm{ }}s,\) điểm chính giữa của lò xo được giữ cố định, sau đó vật dao động điều hòa. Lấy \(g = 10{\rm{ }}m/{s^2}.\) Biết độ cứng của lò xo tỉ lệ nghịch với chiều dài tự nhiên của nó.Tốc độ của vật tại thời điểm \({t_2} = 0,21{\rm{ }}s\) là
Giữ ở giữa coi như \(k = {k_0} = 25N/m{\rm{ }};m = 0,1{\rm{ }}kg \Rightarrow \omega = \sqrt {\frac{k}{m}} = \sqrt {\frac{{25}}{{0,1}}} = 5\pi {\rm{r}}a{\rm{d}}/s \Rightarrow T = 0,4{\rm{s}}\)
Tại \(t = 0,1{\rm{s}}\) ta có \(\left\{ \begin{array}{l}
v = 1,1,m/s\\
x = \frac{{mg}}{k} = 0,04m
\end{array} \right.\)
Tại \(t' = 0,21{\rm{s}}\) là sau \(\frac{T}{4} \Rightarrow v'\left( t \right) = \omega {x_t} = 5\pi .0,04 = 0,2\pi = 20\pi \)
Ở mặt nước, tại hai điểm A và B có hai nguồn kết hợp dao động cùng pha theo phương thẳng đứng. ABCD là hình vuông nằm ngang. Biết trên CD có 3 vị trí mà ở đó các phần tử dao động với biên độ cực đại. Trên AB có tối đa bao nhiêu vị trí mà phần tử ở đó dao động với biên độ cực đại?
+ Số cưc̣ đaị trên CD
\(a - a\sqrt 2 \le k \le a\sqrt 2 - a\)
Chỉ có 3 cưc̣ đaị \( \Rightarrow k = 2 \Rightarrow \frac{{a\left( {\sqrt 2 - 1} \right)}}{\lambda } < 2 \Rightarrow \frac{a}{\lambda } < 4,8\)
+ Số cưc̣ đaị trên AB: \( - a \le k\lambda \le a \Leftrightarrow - 4,8 \le k \le 4,8 \Rightarrow k = - 4; - 3;...;4 \Rightarrow $\) Số cưc̣ đaị là 9
Một sợi dây đàn hồi căng ngang với đầu A cố định đang có sóng dừng. B là phần tử dây tại điểm bụng thứ hai tính từ đầu A, C là phần tử dây nằm giữa A và B. Biết A cách vị trí cân bằng của B và vị trí cân bằng của C những khoảng lần lượt là 30cm và 5cm, tốc độ truyền sóng trên dây là 50cm/s. Trong quá trình dao động điều hoà, khoảng thời gian ngắn nhất giữa hai lần li độ của B có giá trị bằng biên độ dao động của C là
\(AB = \frac{{3\lambda }}{4} = 30 \Rightarrow \lambda = 40cm\)
C cách A 5cm \( \Rightarrow AC = \frac{\lambda }{8}\)
Biên đô ̣của C là: \({A_C} = 2{\rm{a}}\left| {cos\left( {\frac{{2\pi {\rm{d}}}}{\lambda } + \frac{\pi }{2}} \right)} \right| = A\frac{{\sqrt 2 }}{2}\)
Khoảng thời gian ngắn nhất giữa hai lần li độ của B có giá trị bằng biên độ của C là: \(\Delta {t_{min}} = T/4\)
Măṭ khác: \(v = 50cm/s;{\rm{ }}\lambda = 40cm \Rightarrow T = 0,8s \Rightarrow \Delta {t_{min}} = T/4 = 1/5{\rm{ }}\left( s \right)\)
Đặt điện áp xoay chiều \(u = {U_0}cos\omega t\) vào hai đầu đoạn mạch mắc nối tiếp gồm điện trở, cuộn cảm thuần và tụ điện có điện dung C thay đổi được. Ban đầu, khi \(C = {C_0}\) thì điện áp hiệu dụng ở hai đầu điện trở, ở hai đầu cuộn cảm và ở hai đầu tụ điện đều bằng 40V. Giảm dần giá trị điện dung C từ giá trị C0 đến khi tổng điện áp hiệu dụng ở hai đầu tụ điện và điện áp hiệu dụng ở hai đầu cuộn cảm bằng 60V. Khi đó, điện áp hiệu dụng ở hai đầu điện trở có giá trị gần nhất với giá trị nào sau đây?
Theo bài ra ta có
\(\begin{array}{l}
C = {C_0} \Rightarrow {U_L} = {U_R} = {U_{{C_0}}} \Rightarrow R = {Z_L} = {Z_{{C_0}}}\\
\Rightarrow U = 40V
\end{array}\)
Ta có
\(\begin{array}{l}
{U_C} + {U_L} = 60V \Rightarrow {U_{{R_2}}} = {U_L}\\
\Rightarrow \left\{ \begin{array}{l}
{U_C} + {U_{{R_2}}} = 60V \Rightarrow {U_C} = 60 - {U_{{R_2}}}\\
U_{{R_2}}^2 + {\left( {{U_L} - {U_C}} \right)^2} = {40^2}
\end{array} \right.\\
\Rightarrow U_{{R_2}}^2 + U_L^2 + U_C^2 - 2{U_L}{U_C} = {40^2}\\
\Rightarrow U_{{R_2}}^2 + U_{{R_2}}^2 + {\left( {60 - U_{{R_2}}^{}} \right)^2} - 2{\left( {60 - U_{{R_2}}^{}} \right)^2}U_{{R_2}}^{} = {40^2}\\
\Rightarrow U_{{R_2}}^{} = 10.73 \approx 11V
\end{array}\)
Cho dòng điện xoay chiều chạy qua đoạn mạch AB có sơ đồ như hình bên, trong đó L là cuộn cảm thuần và X là đoạn mạch xoay chiều. Khi đó, điện áp giữa hai đầu các đoạn mạch AN và MB có biểu thức lần lượt \({u_{AN}} = 30\sqrt 2 cos\omega t\left( V \right);\,\,\,{u_{MB}} = 40\sqrt 2 cos\left( {\omega t - \frac{\pi }{2}} \right)\left( V \right).\) Điện áp hiệu dụng giữa hai đầu đoạn mạch AB có giá trị nhỏ nhất là
\(\begin{array}{l}
{u_{AN}} = {u_C} + {u_X}\\
{u_{MB}} = {u_C} + {u_X}\\
{u_{AB}} = {u_{AN}} + {u_C}\\
{U_{AB}} \ge OH \Rightarrow {\left( {{U_{AB}}} \right)_{\min }} = OH
\end{array}\)
Áp dụng hệ thức lượng trong tam giác vuông ta có:
\(\frac{1}{{U_{AB}^2}} = \frac{1}{{U_{AN}^2}} + \frac{1}{{U_{MB}^2}} \Rightarrow {U_{AB}} = 24V\)
Điện năng được truyền từ một trạm phát điện có điện áp 10kV đến nơi tiêu thụ bằng đường dây tải điện một pha. Biết công suất truyền đi là 500kW, tổng điện trở đường dây tải điện là \(20\Omega \) và hệ số công suất của mạch điện bằng 1. Hiệu suất của quá trình truyền tải này bằng
Hiêụ suất của quá trình truyền tải: \(H = \frac{{P - \Delta P}}{P} = \frac{{P - \frac{{{P^2}R}}{{{U^2}}}}}{P} = 1 - \frac{{PR}}{{{U^2}}} = 1 - \frac{{{{500.10}^{ - 3}}.20}}{{{{\left( {{{10.10}^3}} \right)}^2}}} = 90\% \)
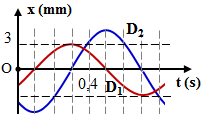
Đặt điện áp xoay chiều \(u = {U_0}cos\left( {\omega t + \varphi } \right)\) vào hai đầu đoạn mạch AB gồm điện trở \(R = 24{\rm{ }}\Omega ,\) tụ điện và cuộn cảm thuần mắc nối tiếp (hình H1) Ban đầu khóa K đóng, sau đó khóa K mở. Hình H2 là đồ thị biểu diễn sự phụ thuộc của cường độ dòng điện i trong đoạn mạch vào thời gian t. Giá trị của U0 gần nhất với giá trị nào sau đây?
\(\begin{array}{l}
\frac{{U_0^2}}{{{3^2}}} = R_0^2 + Z_L^2 \Rightarrow Z_L^2 = \frac{{U_0^2}}{{{3^2}}} - 5,76\\
\frac{{U_0^2}}{{{4^2}}} = R_0^2 + {\left( {Z_L^{} - {Z_C}} \right)^2} \Rightarrow {\left( {Z_L^{} - {Z_C}} \right)^2} = \frac{{U_0^2}}{{{4^2}}} - 5,76\\
R_0^2 = {Z_L}\left( {{Z_L} - {Z_C}} \right) \Rightarrow \frac{{R_0^3}}{{Z_0^2}} = \frac{{{Z_L} - {Z_C}}}{{{Z_L}}} \Rightarrow \frac{{\frac{{U_0^2}}{{{4^2}}} - 5,76}}{{\frac{{U_0^2}}{{{3^2}}} - 5,76}} = {\left( {\frac{{{R^2}}}{{Z_L^2}}} \right)^2}\\
\Rightarrow \left( {\frac{{U_0^2}}{{{4^2}}} - 5,76} \right)\left( {\frac{{U_0^2}}{{{3^2}}} - 5,76} \right) = {R^4}\left( {\frac{{U_0^2}}{{{3^2}}} - 5,76} \right) \Rightarrow \left( {\frac{{U_0^2}}{{{4^2}}} - 5,76} \right)\left( {\frac{{U_0^2}}{{{3^2}}} - 5,76} \right) = {R^4}\\
\Rightarrow \frac{{U_0^4}}{{{3^2}{{.4}^2}}} - 5,76\left( {\frac{{U_0^2}}{{{3^2}}} + \frac{{U_0^2}}{{{4^2}}}} \right) = 0 \Rightarrow {U_0} = R\sqrt {{3^2} + {4^2}} = 120V
\end{array}\)
Trong thí nghiệm Y-âng về giao thoa ánh sáng, nguồn sáng phát ra ánh sáng trắng có bước sóng từ 380nm đến 760nm. Trên màn quan sát, tại điểm M có đúng 4 bức xạ cho vân sáng có bước sóng 735 nm; 490 nm; \({\lambda _1}\) và \({\lambda _2}\) Tổng giá trị \({\lambda _1} + {\lambda _2}\) bằng
Tại điểm M có 4 bức xa ̣cho vân sáng có bước sóng 735nm; 490nm ; \({\lambda _1}\) và \({\lambda _2}\)
Vân trùng nhau của bức xa ̣735nm và 490nm thoả mãn:
\({k_1}.735 = {k_2}.490 \Rightarrow \frac{{{k_1}}}{{{k_2}}} = \frac{{490}}{{735}} = \frac{2}{3} \Rightarrow \left\{ \begin{array}{l}
{k_1} = 2n\\
{k_2} = 3n
\end{array} \right. \Rightarrow {x_M} = \frac{{2n.725.D}}{a} = \frac{{1470nD}}{a}\)
Tại M ngoài 2 bức xa ̣ 735nm và 490nm cho vân sáng thì còn có bức xa ̣ khác của ánh sáng trắng cũng cho vân sáng tại M => Vị trí điểm M: \({x_M} = \frac{{1470nD}}{a} = \frac{{k\lambda D}}{a} \Rightarrow \lambda = \frac{{1470nD}}{k}\)
Mà ánh sáng trắng có bước sóng từ 380nm đến 760nm
\( \Rightarrow 380 \le \frac{{1470n}}{k} \le 760 \Leftrightarrow 1,93n \le k \le 3,87n\)
+ Với \(n = 1:1,93 \le k \le 3,87 \Rightarrow k = 2;3 \Rightarrow $\) Tại M có 2 bức xa ̣cho vân sáng ⇒ n=1 không thoả mãn
+ Với \(n = 2:3,86 \le k \le 7,74 \Rightarrow k = 4,5,6,7 \Rightarrow \) Tại M có 4 bức xa ̣cho vân sáng với bước sóng tương ứng: \(\frac{{1470.2}}{4}{\rm{ = }}735nm;\,\,\,\frac{{1470.2}}{5}{\rm{ = 588nm;}}\,\,\,\frac{{1470.2}}{6}{\rm{ = 490nm; }}\,\,\,\frac{{1470.2}}{7} = 420nm\)
Vâỵ taị M có 4 bức xa ̣ cho vân sáng là :
\(735nm{\rm{ }};{\rm{ }}588nm{\rm{ }};{\rm{ }}490nm{\rm{ }};{\rm{ }}420nm \Rightarrow {\lambda _1} + {\lambda _2} = 1008nm\)
Hạt nhân X phóng xạ biến đổi thành hạt nhân bền Y. Ban đầu (t=0) có một mẫu chất X nguyên chất. Tại thời điểm t1 và t2 tỉ số giữa số hạt nhân Y và số hạt nhân X ở trong mẫu tương ứng là 2 và 3. Tại thời điểm \({t_3} = 2{t_1} + 3{t_2},\) tỉ số đó là
Ta có \(\left\{ \begin{array}{l}
{N_Y} = {N_0}\left( {1 - {2^{ - \frac{t}{T}}}} \right)\\
{N_X} = {N_0}{2^{ - \frac{t}{T}}}
\end{array} \right.\)
+ Thời điểm \({t_1}:\frac{{{N_Y}}}{{{N_X}}} = \frac{{1 - {2^{ - \frac{{{t_1}}}{T}}}}}{{{2^{ - \frac{{{t_1}}}{T}}}}} = 2 \Rightarrow {2^{ - \frac{{{t_1}}}{T}}} = \frac{1}{3}\left( 1 \right)\)
+ Thời điểm \({t_2}:\frac{{{N_Y}}}{{{N_X}}} = \frac{{1 - {2^{ - \frac{{{t_2}}}{T}}}}}{{{2^{ - \frac{{{t_2}}}{T}}}}} = 2 \Rightarrow {2^{ - \frac{{{t_2}}}{T}}} = \frac{1}{4}\left( 2 \right)\)
+ Thời điểm \({t_3} = 2{t_1} + 3{t_2}:\frac{{{N_Y}}}{{{N_X}}} = \frac{{1 - {2^{ - \frac{{2{t_1} + 3{t_2}}}{T}}}}}{{{2^{ - \frac{{2{t_1} + 3{t_2}}}{T}}}}} = \frac{{1 - {2^{ - \frac{{2{t_1}}}{T}}}{{.2}^{ - \frac{{3{t_2}}}{T}}}}}{{{2^{ - \frac{{2{t_1}}}{T}}}{{.2}^{ - \frac{{3{t_2}}}{T}}}}} = \frac{{1 - {{\left( {{2^{ - \frac{{{t_1}}}{T}}}} \right)}^2}.{{\left( {{2^{ - \frac{{{t_2}}}{T}}}} \right)}^3}}}{{{{\left( {{2^{ - \frac{{{t_1}}}{T}}}} \right)}^2}.{{\left( {{2^{ - \frac{{{t_2}}}{T}}}} \right)}^3}}}\left( 3 \right)\)
Thay (1) và (2) vào (3) \(\frac{{{N_Y}}}{{{N_X}}} = 575\)
Khi bắn hạt \(\alpha \) có động năng K vào hạt nhân \({}_{7{\rm{ }}}^{14}N\) đứng yên thì gây ra phản ứng \({}_2^4He + {}_7^{14}N \to {}_8^{16}O + X.\) Cho khối lượng các hạt nhân trong phản ứng lầ n lượt là \({m_{He}} = 4,0015{\rm{ }}u,{\rm{ }}{m_N} = 13,9992{\rm{ }}u,\,\,{m_O} = 16,9947{\rm{ }}u\) và \({m_X} = 1,0073{\rm{ }}u.\) Lấy \(1u = 931,5{\rm{ }}MeV/{c^2}.\) Nếu hạt nhân X sinh ra đứng yên thì giá trịcủa K bằng
Phản ứng thu năng lượng \(\Delta {E_{thu}} = 1,21MeV\)
Áp dụng định luật bảo toàn động lượng ta có
\(\begin{array}{l}
{p_\alpha } = {p_O} \Rightarrow {m_\alpha }.{v_\alpha } = {m_O}{v_O}\\
\Rightarrow \frac{{{m_\alpha }}}{{{m_O}}} = \frac{{{v_\alpha }}}{{{v_O}}} \Rightarrow \frac{K}{{{K_O}}} = \frac{{{m_\alpha }v_\alpha ^2}}{{{m_O}v_O^2}} = \frac{{{m_\alpha }}}{{{m_O}}}.\frac{{v_\alpha ^2}}{{v_O^2}}\\
\Rightarrow \frac{K}{{{K_O}}}\frac{{{m_\alpha }}}{{{m_O}}} \Rightarrow {K_O} = \frac{{K.{m_\alpha }}}{{{m_O}}}
\end{array}\)
Áp dụng định luật bảo toàn năng lượng ta có
\(\begin{array}{l}
K = \Delta {E_{thu}} = {K_O} \Rightarrow K - \Delta {E_{thu}} = K.\frac{{{m_\alpha }}}{{{m_O}}}\\
\Rightarrow K\left( {1 - \frac{{{m_\alpha }}}{{{m_O}}}} \right) = \Delta {E_{thu}} \Rightarrow K = \frac{{\Delta {E_{thu}}}}{{1 - \frac{{{m_\alpha }}}{{{m_O}}}}} = 1,58MeV
\end{array}\)

.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
