Lý thuyết
Lý Thuyết Lớp 12
Lý thuyết lớp 11
Lý thuyết lớp 10
Lý thuyết lớp 9
Lý thuyết lớp 8
Lý thuyết lớp 7
Lý thuyết lớp 6
Lý thuyết lớp 5
Lý thuyết lớp 4
Lý thuyết lớp 3
Lý thuyết lớp 2
Lý thuyết lớp 1
Công thức
Công thức Toán học
Soạn văn
Toán THPT
Toán THCS
Thi vào lớp 10
Tuyển sinh
Đại học
Bản tin
Thư viện câu hỏi
Thi Online
Hỏi bàiĐề thi minh họa THPT QG môn Toán năm 2018 - Bộ GD & ĐT
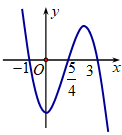
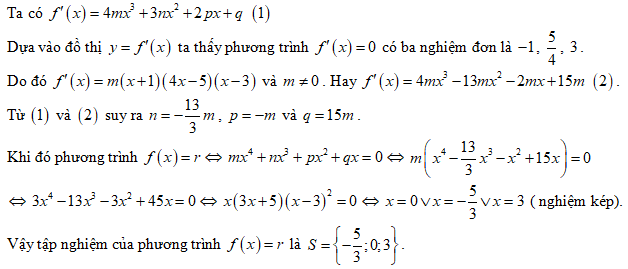Đề thi minh họa THPT QG môn Toán năm 2018 - Bộ GD & ĐT
-
Hocon247
-
50 câu hỏi
-
90 phút
-
47 lượt thi
-
Trung bình
Tham gia [ Hs Hocon247.com ] - Cộng Đồng Luyện Thi Trực Tuyến để được học tập những kiến thức bổ ích từ HocOn247.com
.PNG)
Trong không gian Oxyz, cho hai điểm \(A\left( {1;\,1;\, - 1} \right)\) và \(B\left( {2;\,3;\,2} \right)\). Véctơ \(\overrightarrow {AB} \) có tọa độ là
Ta có \(\overrightarrow {AB} = \left( {1;\,2;\,3} \right)\)
Cho hàm số \(y=f(x)\) có đồ thị như hình vẽ bên. Hàm số đã cho đồng biến trên khoảng nào dưới đây?
.PNG)
Quan sát đồ thị ta thấy đồ thị đi lên trong khoảng \(\left( { - 1;0} \right)\) và \(\left( {1; + \infty } \right)\).
Vậy hàm số đồng biến trên \(\left( { - 1;0} \right)\) và \(\left( {1; + \infty } \right)\).
Quan sát đáp án chọn \(\left( { - 1;0} \right)\)
Với \(a\) và \(b\) là hai số thực dương tùy ý, \(\log \left( {a{b^2}} \right)\) bằng
Ta có \(\log \left( {a{b^2}} \right) = \log a + \log {b^2} = \log a + 2\log \left| b \right| = \log a + 2\log b\) ( vì \(b\) dương)
Cho \(\int\limits_0^1 {f\left( x \right){\rm{d}}x} = 2\) và \(\int\limits_0^1 {g\left( x \right){\rm{d}}x} = 5\) khi đó \(\int\limits_0^1 {\left[ {f\left( x \right) - 2g\left( x \right)} \right]{\rm{d}}x} \) bằng
Ta có \(\int\limits_0^1 {g\left( x \right){\rm{d}}x} = 5 \Leftrightarrow 2\int\limits_0^1 {g\left( x \right){\rm{d}}x} = 10 \Leftrightarrow \int\limits_0^1 {2g\left( x \right){\rm{d}}x} = 10\)
Xét \(\int\limits_0^1 {\left[ {f\left( x \right) - 2g\left( x \right)} \right]{\rm{d}}x} = \int\limits_0^1 {f\left( x \right){\rm{d}}x} - \int\limits_0^1 {2g\left( x \right){\rm{d}}x} = 2 - 10 = - 8\) .
Thể tích khối cầu bán kính \(a\) bằng
\(V = \frac{{4\pi {R^3}}}{3} = \frac{{4\pi {a^3}}}{3}\)
Tập nghiệm của phương trình \({\log _2}\left( {{x^2} - x + 2} \right) = 1\) là
Ta có: \({\log _2}\left( {{x^2} - x + 2} \right) = 1 \Leftrightarrow {x^2} - x + 2 = 2 \Leftrightarrow \left[ \begin{array}{l}
x = 0\\
x = 1
\end{array} \right.\)
Họ nguyên hàm của hàm số \(f\left( x \right) = {{\rm{e}}^x} + x\)
Ta có \(\int {\left( {{{\rm{e}}^x} + x} \right){\rm{d}}x} = {{\rm{e}}^x} + \frac{1}{2}{x^2} + C\)
Trong không gian Oxyz, đường thẳng \(d:\frac{{x - 1}}{2} = \frac{{y - 2}}{{ - 1}} = \frac{{z - 3}}{2}\) đi qua điểm nào sau đây?
Thay tọa độ điểm P vào phương trình d ta được: \(\frac{{1 - 1}}{2} = \frac{{2 - 2}}{{ - 1}} = \frac{{3 - 3}}{2}\) (đúng).
Vậy đường thẳng d đi qua điểm \(P\left( {1;2;3} \right)\).
Với \(k\) và \(n\) là hai số nguyên dương tùy ý thỏa mãn \(k \le n\), mệnh đề nào dưới đây đúng?
Số các số tổ hợp chập k của n được tính theo công thức: \(C_n^k = \frac{{n!}}{{k!\left( {n - k} \right)!}}\). (SGK 11)
Cho cấp số cộng \((u_n)\) có số hạng đầu \(u_1=2\) và công sai \(d=5\). Giá trị của \(u_4\) bằng
Ta có: \({u_4} = {u_1} + 3d = 2 + 3.5 = 17\)
Điểm nào trong hình vẽ bên dưới là điểm biểu diễn số phức \(z = - 1 + 2i\)?
.PNG)
Số phức \(z = - 1 + 2i\) có điểm biểu diễn là điểm \(Q\left( { - 1;2} \right)\).
.PNG)
.PNG)
Cho hàm số \(y=f(x)\) liên tục trên đoạn \([-1;3]\) và có đồ thị như hình bên. Gọi \(M\)và \(m\) lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn \([-1;3]\). Giá trị của \(M-m\) bằng
.PNG)
Từ đồ thị hàm số \(y=f(x)\) trên đoạn \([-1;3]\) ta có:
\(M = \mathop {\max }\limits_{\left[ { - 1;3} \right]} y = f\left( 3 \right) = 3\) và \(m = \mathop {\min }\limits_{\left[ { - 1;3} \right]} y = f\left( 2 \right) = - 2\)
Khi đó \(M - m = 5\).
Tìm các số thực \(a\) và \(b\) thỏa mãn \(2a + \left( {b + i} \right)i = 1 + 2i\) với \(i\) là đơn vị ảo.
Ta có
\(\begin{array}{l}
2a + \left( {b + i} \right)i = 1 + 2i \Leftrightarrow \left( {2a - 1} \right) + bi = 1 + 2i\\
\Leftrightarrow \left\{ \begin{array}{l}
2a - 1 = 1\\
b = 2
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
a = 1\\
b = 2
\end{array} \right.
\end{array}\)
Trong không gian Oxyz, cho hai điểm \(I\left( {1;1;1} \right)\) và \(A\left( {1;2;3} \right)\). Phương trình của mặt cầu có tâm \(I\) và đi qua điểm \(A\) là
Mặt cầu có bán kính \(R = IA = \sqrt {0 + 1 + 4} = \sqrt 5 \).
Suy ra phương trình mặt cầu là \({\left( {x - 1} \right)^2} + {\left( {y - 1} \right)^2} + {\left( {z - 1} \right)^2} = 5\).
Đặt \(a = {\log _3}2\), khi đó \({\log _{16}}27\) bằng
Ta có: \({\log _{16}}27 = \frac{3}{4}{\log _2}3 = \frac{3}{4}.\frac{1}{{{{\log }_3}2}} = \frac{3}{{4a}}\)
Kí hiệu \(z_1, z_2\) là hai nghiệm phức của phương trình \({z^2} - 3{\rm{z}} + 5 = 0\). Giá trị của \(\left| {{z_1}} \right| + \left| {{z_2}} \right|\) bằng
Ta có : \({z^2} - 3z + 5 = 0 \Leftrightarrow \left[ \begin{array}{l}
{z_1} = \frac{{3 + \sqrt {11} i}}{2}\\
{z_2} = \frac{{3 - \sqrt {11} i}}{2}
\end{array} \right.\). Suy ra \(\left| {{z_1}} \right| = \left| {{z_2}} \right| = \sqrt 5 \Rightarrow \left| {{z_1}} \right| + \left| {{z_2}} \right| = 2\sqrt 5 \).
Trong không gian Oxyz, khoảng cách giữa hai mặt phẳng \(\left( P \right):x + 2y + 2z - 10 = 0\) và \(\left( Q \right):x + 2y + 2z - 3 = 0\) bằng
Lấy điểm \(M\left( {0;0;5} \right) \in \left( P \right)\).
Do \(\left( P \right)\,{\rm{//}}\,\left( Q \right)\) nên \({\rm{d}}\left( {\left( P \right),\left( Q \right)} \right) = {\rm{d}}\left( {M,\left( Q \right)} \right) = \frac{{\left| {{x_M} + 2{y_M} + 2{z_M} - 3} \right|}}{{\sqrt {{1^2} + {2^2} + {2^2}} }} = \frac{7}{3}\).
Tập nghiệm của bất phương trình \({3^{{x^2} - 2x}} < 27\) là
Bất phương trình tương đương với \({3^{{x^2} - 2x}} < {3^3} \Leftrightarrow {x^2} - 2x < 3\)
\( \Leftrightarrow {x^2} - 2x - 3 < 0 \Leftrightarrow - 1 < x < 3\).
Diện tích phần hình phẳng gạch chéo trong hình vẽ bên được tính theo công thức nào dưới đây?
.PNG)
Ta thấy \(\forall x \in \left[ { - 1;2} \right]: - {x^2} + 3 \ge {x^2} - 2x - 1\) nên \(S = \int\limits_{ - 1}^2 {\left[ {\left( { - {x^2} + 3} \right) - \left( {{x^2} - 2x - 1} \right)} \right]} \,{\rm{d}}x = \int\limits_{ - 1}^2 {\left( { - 2{x^2} + 2x + 4} \right)} \,{\rm{d}}x\)
Cho khối nón có độ dài đường sinh bằng \(2a\) và bán kính đáy bằng \(a\). Thể tích của khối nón đã cho bằng
Ta có chiều cao của khối nón bằng \(h = \sqrt {{l^2} - {r^2}} \) với \(\left\{ \begin{array}{l}
l = 2a\\
r = a
\end{array} \right.\). Suy ra \(h = a\sqrt 3 \).
Vậy thể tích khối nón là \(V = \frac{1}{3}\pi {r^2}h = \frac{1}{3}\pi {a^2}a\sqrt 3 = \frac{{\pi {a^3}\sqrt 3 }}{3}\).
Cho hàm số \(y=f(x)\) có bảng biến thiên như sau
.PNG)
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là
Vì \(\mathop {\lim }\limits_{x \to + \infty } \,f\left( x \right) = 5\) \( \Rightarrow \) đường thẳng \(y=5\) là tiệm cận ngang của đồ thị hàm số.
Vì \(\mathop {\lim }\limits_{x \to - \infty } \,f\left( x \right) = 2 \Rightarrow \) đường thẳng \(y=2\) là tiệm cận ngang của đồ thị hàm số.
Vì \(\mathop {\lim }\limits_{x \to {1^ - }} \,f\left( x \right) = + \infty \Rightarrow \) đường thẳng \(x=1\) là tiệm cận đứng của đồ thị hàm số.
KL: Đồ thị hàm số có tổng số ba đường tiệm cận.
.PNG)
Hàm số \(f\left( x \right) = {\log _2}\left( {{x^2} - 2x} \right)\) có đạo hàm
Áp dụng công thức \({\left( {{{\log }_a}u\left( x \right)} \right)^\prime } = \frac{{u'\left( x \right)}}{{u\left( x \right).\ln a}}\).
Vậy \(f'\left( x \right) = \frac{{{{\left( {{x^2} - 2x} \right)}^\prime }}}{{\left( {{x^2} - 2x} \right)\ln 2}} = \frac{{2x - 2}}{{\left( {{x^2} - 2x} \right)\ln 2}}\).
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
Cho \(\int\limits_0^1 {\frac{{x{\rm{d}}x}}{{{{\left( {x + 2} \right)}^2}}}} = a + b\ln 2 + c\ln 3\) với \(a, b, c\) là các số hữu tỷ. Giá trị của \(3a+b+c\) bằng
\(\int\limits_0^1 {\frac{{x{\rm{d}}x}}{{{{\left( {x + 2} \right)}^2}}}} = \int\limits_0^1 {\frac{{\left( {x + 2} \right) - 2}}{{{{\left( {x + 2} \right)}^2}}}{\rm{d}}x = \int\limits_0^1 {\frac{{{\rm{d}}x}}{{x + 2}}} } - \int\limits_0^1 {\frac{{2{\rm{d}}x}}{{{{\left( {x + 2} \right)}^2}}}} \)
\( = \left. {\ln \left( {x + 2} \right)} \right|_0^1 - \left. {2.\frac{{{{\left( {x + 2} \right)}^{ - 1}}}}{{ - 1}}} \right|_0^1 = \ln 3 - \ln 2 + \frac{2}{3} - 1 = - \frac{1}{3} - \ln 2 + \ln 3\)
Vậy \(a = - \frac{1}{3};b = - 1;c = 1 \Rightarrow 3a + b + c = - 1\)
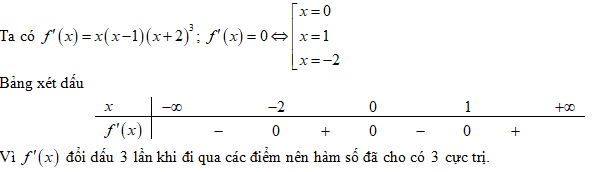
.PNG)
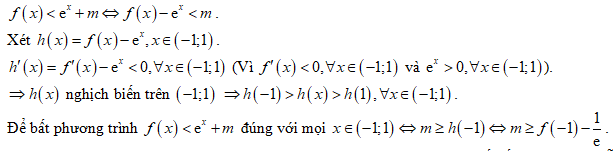
.PNG)
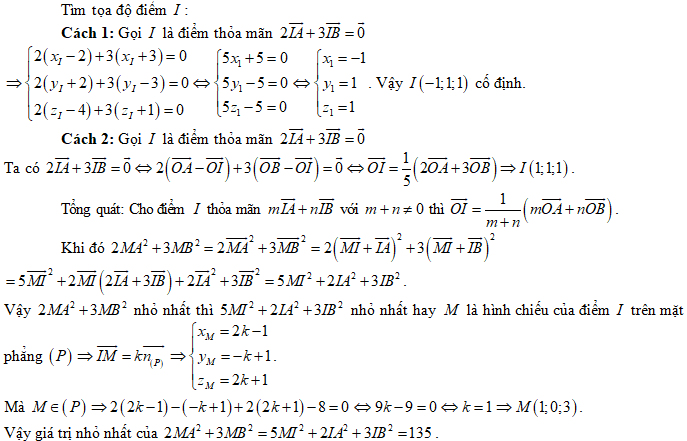
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
