Đề thi thử THPT QG năm 2021 môn Toán - Trường THPT Thanh Oai A
Đề thi thử THPT QG năm 2021 môn Toán - Trường THPT Thanh Oai A
-
Hocon247
-
50 câu hỏi
-
90 phút
-
61 lượt thi
-
Trung bình
Tham gia [ Hs Hocon247.com ] - Cộng Đồng Luyện Thi Trực Tuyến để được học tập những kiến thức bổ ích từ HocOn247.com
Từ một nhóm có 10 học sinh. Có bao nhiêu cách chọn ra 3 học sinh và xếp thành một hàng ngang?
Số cách chọn ra 3 học sinh từ 10 học sinh là \(C_{10}^{3}\).
Số cách xếp 3 học sinh đã chọn vào 3 vị trí là 3!
Vậy số cách chọn ra 3 học sinh và xếp thành một hàng ngang là \(3!\times C_{10}^{3}=A_{10}^{3}\)
Cho cấp số cộng \(\left( {{u}_{n}} \right)\) có \({{u}_{5}}=6\) và công sai d=1. Giá trị của \({{u}_{3}}\) bằng
\(6 = {u_5} \Leftrightarrow 6 = {u_3} + 2d \Leftrightarrow 6 = {u_3} + 2 \Leftrightarrow {u_3} = 4\)
Cho hàm số \(f\left( x \right)\) có bảng biến thiên như sau:
Hàm số đã cho nghịch biến trên khoảng nào, trong các khoảng dưới đây?
Từ bảng biến thiên suy ra hàm số đã cho nghịch biến trên khoảng \(\left( -\infty ;-2 \right).\)
Cho hàm số \(f\left( x \right)\) có bảng biến thiên như sau:
Điểm cực đại của đồ thị hàm số đã cho là
Từ bảng biến thiên suy ra đồ thị hàm số có điểm cực đại là (-1;3)
Cho hàm số \(f\left( x \right)\) có bảng xét dấu của đạo hàm \({f}'\left( x \right)\) như sau:
.png)
Hàm số \(f\left( x \right)\) có bao nhiêu điểm cực trị?
Từ bảng xét dấu ta thấy đạo hàm chỉ đổi dấu 2 lần. Vậy hàm số có 2 điểm cực trị.
Tiệm cận đứng của đồ thị hàm số \(y=\frac{-2x+4}{-x+1}\) là đường thẳng:
Ta có:
\(\mathop {\lim }\limits_{x \to {1^ + }} \frac{{ - 2x + 4}}{{ - x + 1}} = - \infty \)
\(\mathop {\lim }\limits_{x \to {1^ - }} \frac{{ - 2x + 4}}{{ - x + 1}} = + \infty \)
Vậy đồ thị hàm số có tiệm cận đứng là đường thẳng x = 1
Hàm số \(y={{x}^{4}}-1\) có đồ thị là hình nào dưới đây?
Ta có: \({y}'=4{{x}^{3}}, {y}'=0\Leftrightarrow 4{{x}^{3}}=0\Leftrightarrow x=0\).
Hàm số đã cho là hàm trùng phương, có một cực trị nên có đồ thị là hình 3.
Đồ thị của hàm số \(y = {\left( {x - 1} \right)^2}\left( {x + 2} \right)\) cắt trục tung tại điểm có tung độ bằng
\(x = 0 \Rightarrow y = {\left( { - 1} \right)^2} \times 2 = 2\)
Với a là số thực dương tùy ý, \(\ln \left( {ea} \right)\) bằng
\(\ln \left( {ea} \right) = \ln e + \ln a = 1 + \ln a\)
Đạo hàm của hàm số \(y = {\pi ^x}\) là
\(y' = {\pi ^x}\ln \pi \)
Với a là số thực dương tùy ý, \(a\sqrt[3]{a}\) bằng
\(a\sqrt[3]{a} = a.{a^{\frac{1}{3}}} = {a^{\frac{4}{3}}}\)
Nghiệm của phương trình \({4^{2x - 1}} = 32\) là
\({4^{2x - 1}} = 32 \Leftrightarrow {2^{2\left( {2x - 1} \right)}} = {2^5} \Leftrightarrow 2\left( {2x - 1} \right) = 5 \Leftrightarrow x = \frac{7}{4}\)
Nghiệm của phương trình \({{\log }_{3}}\left( 1-3x \right)=2\) là
\({\log _3}\left( {1 - 3x} \right) = 2 \Leftrightarrow 1 - 3x = {3^2} \Leftrightarrow x = - \frac{8}{3}\)
Cho hàm số \(f\left( x \right)=-3{{x}^{2}}+1.\) Trong các khẳng định sau, khẳng định nào đúng?
\(\int {f\left( x \right){\rm{d}}x} = \int {\left( { - 3{x^2} + 1} \right){\rm{d}}x} = - {x^3} + x - C\)
Hàm \(F\left( x \right)=\cos 2x+5\) là một nguyên hàm của hàm số nào dưới đây?
\(f\left( x \right) = F'\left( x \right) = - 2\sin 2x\)
Nếu \(\int\limits_{1}^{2}{f\left( x \right)dx=-2}\) và \(\int\limits_{1}^{3}{f\left( x \right)dx=6}\) thì \(\int\limits_{2}^{3}{f\left( x \right)dx}\) bằng
\(6 = \int\limits_1^3 {f\left( x \right){\rm{d}}x \Leftrightarrow 6} = \int\limits_1^2 {f\left( x \right){\rm{d}}x} + \int\limits_2^3 {f\left( x \right){\rm{d}}x} \)
\( \Leftrightarrow 6 = - 2 + \int\limits_2^3 {f\left( x \right){\rm{d}}x} \)
\( \Leftrightarrow \int\limits_2^3 {f\left( x \right){\rm{d}}x} = 8\)
Tích phân \(\int\limits_0^1 {\left( {{x^2} + x} \right)dx} \) bằng
\(\int\limits_0^1 {\left( {{x^2} + x} \right)dx} = \left. {\left( {\frac{{{x^3}}}{3} + \frac{{{x^2}}}{2}} \right)} \right|_0^1 = \left( {\frac{1}{3} + \frac{1}{2}} \right) - 0 = \frac{5}{6}\)
Số phức liên hợp của số phức z = 2021i là
Ta có \(\overline z = - 2021i\)
Cho số phức z=2-3i và \(\text{w}=1+i\). Số phức \(z+2\text{w}\) bằng
\(z + 2w = 2 - 3i + 2\left( {1 + i} \right) = 4 - i\)
Trên mặt phẳng tọa độ, điểm \(M\left( 2;-3 \right)\) biểu diễn số phức nào dưới đây?
Điểm biểu diễn số phức z = 2 - 3i
Cho khối chóp S.ABCD có đáy là hình vuông cạnh đáy bằng a và SA vuông góc với đáy với \(SA=a\sqrt{3}.\) Thể tích của khối chóp S.ABCD bằng
Đáy là hình vuông cạnh bằng a nên diện tích đáy là \({{a}^{2}}\).
Đường cao \(SA=a\sqrt{3}\) nên thể tích của S.ABCD là \(\frac{1}{3}{{a}^{2}}.a\sqrt{3} =\frac{{{a}^{3}}\sqrt{3}}{3}\).
Thể tích khối lập phương có cạnh 3a là
Thể tích khối lập phương là \({\left( {3a} \right)^3}= 27{a^3}\)
Công thức tính thể tích \(V\) của khối trụ có bán kính đáy r và chiều cao h là
Thể tích V của khối trụ có bán kính đáy r và chiều cao h là \(V=\pi {{r}^{2}}h\).
Cho hình trụ có bán kính đáy bằng 3cm, độ dài đường cao bằng 4cm. Diện tích xung quanh của hình trụ bằng
.png)
Ta có \(r=3\text{ cm}, h=l=4\text{ cm}\).
Diện tích xung quanh của hình trụ là \(2\pi .r.l =2\pi .3.4 =24\pi \text{ c}{{\text{m}}^{2}}\).
Trong không gian Oxyz, cho hai điểm \(A\left( 1;2;4 \right)\) và \(B\left( 2;4;-1 \right)\). Tìm tọa độ trọng tâm G của tam giác OAB.
Tọa độ trọng tâm G của tam giác OAB là \(G\left( {\frac{{1 + 2 + 0}}{3};\frac{{2 + 4 + 0}}{3};\frac{{4 - 1 + 0}}{3}} \right)\) \( \Leftrightarrow G\left( {1;2;1} \right)\)
Trong không gian Oxyz, cho mặt cầu \(\left( S \right):{{\left( x+1 \right)}^{2}}+{{\left( y-2 \right)}^{2}}+{{\left( z-1 \right)}^{2}}=9\). Tìm tọa độ tâm I của mặt cầu \(\left( S \right)\).
Mặt cầu \(\left( S \right):{{\left( x-a \right)}^{2}}+{{\left( y-b \right)}^{2}}+{{\left( z-c \right)}^{2}}={{R}^{2}}\) có tâm là \(I\left( a;b;c \right)\), do đó mặt cầu \(\left( S \right):{{\left( x+1 \right)}^{2}}+{{\left( y-2 \right)}^{2}}+{{\left( z-1 \right)}^{2}}=9\) có tâm \(I\left( -1;2;1 \right)\).
Trong không gian Oxyz, cho điểm \(M\left( m;1;6 \right)\) và mặt phẳng \(\left( P \right):x-2y+z-5=0\). Điểm M thuộc mặt phẳng \(\left( P \right)\) khi giá trị của tham số m là
Ta có \(M\left( m;1;6 \right)\) thuộc mặt phẳng \(\left( P \right):x-2y+z-5=0\) khi \(m-2.1+6-5=0 \Leftrightarrow m=1\).
Trong không gian Oxyz, một véctơ chỉ phương của đường thẳng \(d:\frac{x-2}{-1}=\frac{y-1}{2}=\frac{z}{1}\) là
Đường thẳng \(d:\frac{x-{{x}_{0}}}{a}=\frac{y-{{y}_{0}}}{b}=\frac{z-{{z}_{0}}}{c}\) có một véc tơ chỉ phương là \(\vec{u}=\left( a;b;c \right)\), do đó đường thẳng \(d:\frac{x-2}{-1}=\frac{y-1}{2}=\frac{z}{1}\) có một véc tơ chỉ phương là \(\vec{u}=\left( -1;2;1 \right)\).
Gọi S là tập các số tự nhiên có bốn chữ số khác nhau được tạo từ tập \(E=\left\{ 1;2;3;4;5 \right\}\). Chọn ngẫu nhiên một số từ tập S. Tính xác suất để số được chọn là một số lẻ.
Trong 5 số thuộc tập \(E=\left\{ 1;2;3;4;5 \right\}\) có 3 số lẻ nên xác suất cần tìm là \(\frac{3}{5}\).
Hàm số nào sau đây đồng biến trên tập xác định của nó?
Hàm số \(y=\ln x\) có cơ số e>1 nên đồng biến trên tập xác định của nó.
Gọi giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(f\left( x \right)=\frac{x+3}{x-1}\) trên đoạn \(\left[ 2;3 \right]\) lần lượt là M và m. Tổng M+m bằng
Ta có \({f}'\left( x \right)=\frac{-4}{{{\left( x-1 \right)}^{2}}}\) và \({f}'\left( x \right)=0\) vô nghiệm.
Trên đoạn \(\left[ 2;3 \right]\), xét các giá trị \(f\left( 2 \right)=5\) và \(f\left( 3 \right)=3\)
Do đó M=5, m=3 nên M+m=8.
Tập nghiệm của bất phương trình \({\left( {\frac{1}{2}} \right)^{{x^2} - x}} > {2^{x - 4}}\) là
Ta có \({{\left( \frac{1}{2} \right)}^{{{x}^{2}}-x}}>{{2}^{x-4}} \Leftrightarrow {{2}^{-{{x}^{2}}+x}}>{{2}^{x-4}} \Leftrightarrow -{{x}^{2}}+x>x-4\Leftrightarrow {{x}^{2}}-4<0\Leftrightarrow -2<x<2\).
Vậy tập nghiệm của bất phương trình \({{\left( \frac{1}{2} \right)}^{{{x}^{2}}-x}}>{{2}^{x-4}}\) là S=(-2;2).
Cho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\) và \(\int\limits_{0}^{1}{\left[ f\left( x \right)+3{{x}^{2}} \right]\text{d}x}=6\). Khi đó \(\int\limits_{0}^{1}{f\left( x \right)\text{d}x}\) bằng
Ta có \(\int\limits_{0}^{1}{\left[ f\left( x \right)+3{{x}^{2}} \right]\text{d}x}=6 \Leftrightarrow \int\limits_{0}^{1}{f\left( x \right)\text{d}x}+\int\limits_{0}^{1}{3{{x}^{2}}\text{d}x}=6 \Leftrightarrow \int\limits_{0}^{1}{f\left( x \right)\text{d}x}+\left. {{x}^{3}} \right|_{0}^{1}=6\)
\(\Leftrightarrow \int\limits_{0}^{1}{f\left( x \right)\text{d}x}+\left( 1-0 \right)=6 \Leftrightarrow \int\limits_{0}^{1}{f\left( x \right)\text{d}x}=5\).
Cho số phức z=2+3i. Tìm môđun của số phức \(w=\left( 1+i \right)z-\bar{z}\)
Ta có
\(w=\left( 1+i \right)z-\bar{z} =\left( 1+i \right)\left( 2+3i \right)-\left( 2-3i \right) =2+3i+2i+3{{i}^{2}}-2+3i =8i+3\left( -1 \right) =-3+8i\).
Khi đó môđun của số phức \(w=\left( 1+i \right)z-\bar{z}\) là \(\left| w \right|=\sqrt{{{\left( -3 \right)}^{2}}+{{8}^{2}}} =\sqrt{63}\).
Cho hình chóp S.ABC có SA vuông góc với mặt phẳng \(\left( ABC \right)\) và \(SA=a\sqrt{2}\), biết tam giác ABC vuông cân tại B và AC=2a (minh họa như hình vẽ).
.png)
Tính số đo góc giữa đường thẳng SB và mặt phẳng (ABC).
Ta có SB có hình chiếu vuông góc xuống \(\left( ABC \right)\) là AB, do đó góc giữa đường thẳng SB và mặt phẳng \(\left( ABC \right)\) là \(\widehat{SBA}\).
Do tam giác ABC vuông cân tại B và AC=2a nên \(A{{B}^{2}}+B{{C}^{2}}=A{{C}^{2}} \Rightarrow 2A{{B}^{2}}=4{{a}^{2}} \Rightarrow AB=a\sqrt{2}\).
Trong tam giác SAB có \(\tan \widehat{SBA}=\frac{SA}{AB} =1\), do đó \(\widehat{SBA}={{45}^{0}}\).
Vậy số đo góc giữa đường thẳng SB và mặt phẳng \(\left( ABC \right)\) bằng \({{45}^{0}}\).
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B với AB=BC=a, AD=2a. Biết \(SA\bot \left( ABCD \right)\) và SA=a. Tính khoảng cách giữa AD và SB.
.png)
Trong \(\left( SAB \right)\) dựng \(AH\bot SB\) tại H.
Vì \(\left\{ \begin{align} & AD\bot SA \\ & AD\bot AB \\ \end{align} \right.\) \(\Rightarrow AD\bot \left( SAB \right) \Rightarrow AD\bot AH\).
Khi đó \(d\left( AD,SB \right)=AH\).
Xét tam giác SAB vuông tại A có \(AH=\frac{SA.AB}{\sqrt{S{{A}^{2}}+A{{B}^{2}}}}=\frac{a\sqrt{2}}{2}\).
Trong không gian Oxyz, cho hai điểm \(A\left( 2;1;1 \right), B\left( 0;3;-1 \right)\). Mặt cầu \(\left( S \right)\) đường kính AB có phương trình là
Ta có tâm I của mặt cầu \(\left( S \right)\) là trung điểm của AB nên \(I\left( 1;2;0 \right)\).
Mặt khác mặt cầu \(\left( S \right)\) có bán kính là \(R=\frac{AB}{2} =\frac{\sqrt{{{\left( 0-2 \right)}^{2}}+{{\left( 3-1 \right)}^{2}}+{{\left( -1-1 \right)}^{2}}}}{2} =\frac{\sqrt{12}}{2} =\sqrt{3}\).
Vậy mặt cầu \(\left( S \right)\) đường kính AB có phương trình là \({{\left( x-1 \right)}^{2}}+{{\left( y-2 \right)}^{2}}+{{z}^{2}}=3\).
Trong không gian Oxyz, cho tam giác ABC với \(A\left( 3;1;2 \right), B\left( -3;2;5 \right), C\left( 1;6;-3 \right)\). Khi đó phương trình trung tuyến AM của tam giác ABC là
Do AM là trung tuyến của tam giác ABC nên M là trung điểm của BC, suy ra \(M\left( -1;4;1 \right)\).
Ta có \(\overrightarrow{AM}=\left( -4;3;-1 \right)\) là véc tơ chỉ phương của đường thẳng AM và có AM đi qua điểm \(A\left( 3;1;2 \right)\) nên có phương trình tham số là \(\left\{ \begin{array}{l} x = 1 - 4t\\ y = - 3 + 3t\\ z = 4 - 1t \end{array} \right.\)
Cho \(y=f\left( x \right)\) có đồ thị của \(y={f}'\left( x \right)\) như hình vẽ dưới đây.
Đặt \(M=\underset{\left[ \text{-2;6} \right]}{\mathop{\text{max}}}\,\text{ }f\left( x \right), m=\underset{\left[ \text{-2;6} \right]}{\mathop{\text{min}}}\,\text{ }f\left( x \right)\). Giá trị của biểu thức M+m bằng
Từ đồ thị của \(y={f}'\left( x \right)\), ta có bảng biến thiên của \(y=f\left( x \right)\) trên \(\left[ -2;6 \right]\) như sau
Từ bảng biến thiên ta có
\(M=\underset{\left[ \text{-2;6} \right]}{\mathop{\text{max}}}\,\text{ }f\left( x \right)=\text{max}\left\{ f\left( 0 \right),f\left( 5 \right) \right\}, m=\underset{\left[ \text{-2;6} \right]}{\mathop{\text{min}}}\,\text{ }f\left( x \right)=\text{min}\left\{ f\left( -2 \right),f\left( 2 \right),f\left( 6 \right) \right\}\).
Từ đồ thị của \(y={f}'\left( x \right)\) ta có \(\int\limits_{0}^{2}{\left| {f}'\left( x \right) \right|\text{d}x}<\int\limits_{2}^{5}{\left| {f}'\left( x \right) \right|\text{d}x} \Leftrightarrow \int\limits_{0}^{2}{-{f}'\left( x \right)\text{d}x<\int\limits_{2}^{5}{{f}'\left( x \right)\text{d}x}} \Leftrightarrow f\left( 0 \right)-f\left( 2 \right)<0\)
Suy ra \(\text{max}\left\{ f\left( 0 \right),f\left( 5 \right) \right\}=f\left( 5 \right)\).
Mặt khác, cũng từ từ đồ thị của \(y={f}'\left( x \right)\), ta có \(\int\limits_{-2}^{0}{\left| {f}'\left( x \right) \right|\text{d}x}>\int\limits_{0}^{2}{\left| {f}'\left( x \right) \right|\text{d}x}\Leftrightarrow \int\limits_{-2}^{0}{{f}'\left( x \right)\text{d}x>\int\limits_{0}^{2}{-{f}'\left( x \right)\text{d}x}}\Leftrightarrow f\left( 0 \right)-f\left( -2 \right)>f\left( 0 \right)-f\left( 2 \right)\Leftrightarrow f\left( -2 \right)<f\left( 2 \right)\)
Hơn nữa \(\int\limits_{2}^{5}{\left| {f}'\left( x \right) \right|\text{d}x}>\int\limits_{5}^{6}{\left| {f}'\left( x \right) \right|\text{d}x} \Leftrightarrow \int\limits_{2}^{5}{{f}'\left( x \right)\text{d}x>\int\limits_{5}^{6}{-{f}'\left( x \right)\text{d}x}} \Leftrightarrow f\left( 5 \right)-f\left( 2 \right)>f\left( 5 \right)-f\left( 6 \right) \Leftrightarrow f\left( 2 \right)<f\left( 6 \right)\)
Suy ra \(\text{min}\left\{ f\left( -2 \right),f\left( 2 \right),f\left( 6 \right) \right\}=f\left( -2 \right)\).
Vậy \(\text{M=max}\left\{ f\left( 0 \right),f\left( 5 \right) \right\}=f\left( 5 \right), \text{m=min}\left\{ f\left( -2 \right),f\left( 2 \right),f\left( 6 \right) \right\}=f\left( -2 \right)\),
nên \(M+m=f\left( 5 \right)+f\left( -2 \right)\)
Số giá trị nguyên dương của tham số m thỏa m<10 để bất phương trình \({{3}^{2x+2}}-{{3}^{x}}.({{3}^{m+2}}+1)+{{3}^{m}}<0\) có ít nhất 3 nghiệm nguyên là
Ta có \({{3}^{2x+2}}-{{3}^{x}}.({{3}^{m+2}}+1)+{{3}^{m}}<0\Leftrightarrow \left( {{3}^{x}}-{{3}^{m}} \right)\left( {{3}^{x+2}}-1 \right)<0\).
Do m là số nguyên dương nên \(m\ge 1\), suy ra \({{3}^{x}}-{{3}^{m}}<0\)
Vậy \(\left( {{3}^{x}}-{{3}^{m}} \right)\left( {{3}^{x+2}}-1 \right)<0\)\(\Leftrightarrow \left\{ \begin{matrix} {{3}^{x}}-{{3}^{m}}<0 \\ {{3}^{x+2}}-1>0 \\ \end{matrix} \right.\)
\(\Leftrightarrow \left\{ \begin{matrix} x<m \\ x>-2 \\ \end{matrix} \right.\).
Nên tập nghiệm của \({{3}^{2x+2}}-{{3}^{x}}.({{3}^{m+2}}+1)+{{3}^{m}}<0\) là \(S=\left( -2;m \right)\), với m là số nguyên dương thỏa m<10. Khi đó \(S=\left( -2;m \right)\) có ít nhất 3 nghiệm nguyên thì $<m<10.
Vậy có 8 giá trị nguyên dương của m thỏa mãn đề bài.
Giả sử hàm số f liên tục trên đoạn [0;2] thỏa mãn \(\int\limits_{0}^{1}{f(x)\text{dx}}=6, \int\limits_{1}^{2}{f(x)\text{dx}}=-2\). Giá trị của tích phân \(\int\limits_{0}^{{\pi }/{2}\;}{f(2\sin x)\cos x\text{dx}}\) là
Đặt \(t=2\sin x \Rightarrow \text{dt}=2\cos x\text{dx}\) và
.png)
Khi đó
\(\int\limits_{0}^{{\pi }/{2}\;}{f(2\sin x)\cos x\text{dx}} =\int\limits_{0}^{2}{\frac{f(t)}{2}\text{dt}} =\frac{1}{2}\int\limits_{0}^{2}{f(t)\text{dt}} =\frac{1}{2}\left( \int\limits_{0}^{1}{f(t)\text{dt}}+\int\limits_{1}^{2}{f(t)\text{dt}} \right) =\frac{1}{2}\left( 6+\left( -2 \right) \right) =2\).
Vậy \(\int\limits_{0}^{{\pi }/{2}\;}{f(2\sin x)\cos x\text{dx}}=2\)
Cho số phức \(z=a+bi\text{ }\left( a,b\in \mathbb{R} \right)\) thỏa mãn \(\left| z \right|=5\) và \(z\left( 2+i \right)\left( 1-2i \right)\) là một số thực. Tính giá trị của \(P=\left| a \right|+\left| b \right|\).
Ta có \(\left| z \right|=5\Leftrightarrow {{a}^{2}}+{{b}^{2}}=25\) (1)
Ta có \(z\left( 2+i \right)\left( 1-2i \right)= \left( a+bi \right)\left( 4-3i \right)= \left( 4a+3b \right)+\left( -3a+4b \right)i\).
Vì \(\(z\left( 2+i \right)\left( 1-2i \right)\) là một số thực \(-3a+4b=0\Leftrightarrow b=\frac{3a}{4}\) (2).
Thế (2) vào (1) ta được \({{a}^{2}}+\frac{9}{16}{{a}^{2}}=25\Leftrightarrow {{a}^{2}}=16\Rightarrow a=\pm 4\Rightarrow b=\pm 3\).
Vậy \(P=\left| a \right|+\left| b \right|=7\).
Cho hình chóp S.ABC có ABC là tam giác đều và cạnh bên SA vuông góc với đáy, với \(SA=\frac{a}{2}\). Góc tạo bởi mặt phẳng \(\left( SBC \right)\) và mặt phẳng \(\left( ABC \right)\) bằng \(30{}^\circ \). Thể tích của khối chóp S.ABC bằng
.png)
Gọi M là trung điểm của cạnh BC.
Ta có:
♦ \(AM\bot BC\) (do tam giác ABC đều). \(\left( 1 \right)\)
♦ \(SA\bot \left( ABC \right)\) (theo giả thiết). \(\left( 2 \right)\)
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) suy ra \(SM\bot BC\) (theo định lí ba đường vuông góc).
Nên góc tạo bởi mặt phẳng \(\left( SBC \right)\) và mặt phẳng \(\left( ABC \right)\) bằng góc \(\widehat{SMA} \Rightarrow \widehat{SMA}=30{}^\circ \).
Xét tam giác vuông SMA có \(\widehat{SMA}=30{}^\circ \) và \(AM=\frac{a\sqrt{3}}{2}\) do đó ta có \(\tan \widehat{SMA}=\frac{SA}{AM} \Rightarrow AM=\frac{SA}{\tan \widehat{SMA}} \Rightarrow AM=\frac{\frac{a}{2}}{\tan 30{}^\circ }\) nên \(AM=\frac{a\sqrt{3}}{2}\).
Trong tam giác vuông ABM tại M ta có \(B{{M}^{2}}+A{{M}^{2}}=A{{B}^{2}}\), mà AB=2BM nên có \(B{{M}^{2}}+A{{M}^{2}}=4B{{M}^{2}} \Rightarrow 3B{{M}^{2}}=A{{M}^{2}} \Rightarrow BM=\frac{1}{\sqrt{3}}AM\) hay \(\Rightarrow BM=\frac{1}{\sqrt{3}}\frac{a\sqrt{3}}{2}=\frac{a}{2}\), do đó \(\Rightarrow BC=a\)
Diện tích tam giác ABC là \({{S}_{ABC}}= \frac{1}{2}BC.AM =\frac{1}{2}a.\frac{a\sqrt{3}}{2} =\frac{{{a}^{2}}\sqrt{3}}{4}\).
Vậy thể tích của khối chóp S.ABC là \({{V}_{S.ABC}}=\frac{1}{3}SA.{{S}_{ABC}} =\frac{1}{3}.\frac{a}{2}.\frac{{{a}^{2}}\sqrt{3}}{4} =\frac{{{a}^{3}}\sqrt{3}}{24}\)
Nghiêng một cốc nước hình trụ có đựng nước, người ta thấy bề mặt nước là hình elip có độ dài trục lớn là \(10\,\text{ cm}\), khoảng cách từ hai đỉnh trên trục lớn của elip đến đáy cốc lần lượt là \(5\text{ cm}\) và \(11\,\text{ cm}\). Tính thể tích nước trong cốc.
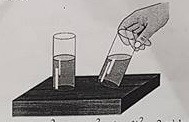
.png)
Ta có \(V={{V}_{1}}+{{V}_{2}}\).
Xét mặt cắt như hình vẽ, ta có \(CE=6\text{ cm}, CD=\sqrt{D{{E}^{2}}-C{{E}^{2}}}=8\text{ cm}\).
Do đó bán kính đáy hình trụ \(r=4\text{ cm}\).
\({{V}_{1}}=\pi {{r}^{2}}h=\pi {{.4}^{2}}.5=80\pi \,\text{c}{{\text{m}}^{\text{3}}}, {{V}_{2}}=\frac{1}{2}\pi {{r}^{2}}l=\frac{1}{2}\pi {{.4}^{2}}.6=48\pi \,\,\text{c}{{\text{m}}^{\text{3}}}\).
Vậy \(V=128\pi \,\text{c}{{\text{m}}^{\text{3}}}\).
Trong không gian Oxyz cho đường thẳng \(\Delta :\frac{x}{1}=\frac{y+1}{2}=\frac{z-1}{1}\) và mặt phẳng \(\left( P \right):x-2y-z+3=0\). Đường thẳng nằm trong \(\left( P \right)\) đồng thời cắt và vuông góc với \(\Delta \) có phương trình là
Ta có \(\Delta :\frac{x}{1} = \frac{{y + 1}}{2} = \frac{{z - 1}}{1}\) \( \Rightarrow \Delta :\left\{ \begin{array}{l} x = t\\ y = - 1 + 2t\\ z = 1 + t \end{array} \right.\)
Gọi \(M=\Delta \cap \left( P \right) \Rightarrow M\in \Delta \Rightarrow M\left( t;2t-1;t+1 \right)\).
Với \(M\in \left( P \right) \Rightarrow t-2\left( 2t-1 \right)-\left( t+1 \right)+3=0 \Leftrightarrow 4-4t=0 \Leftrightarrow t=1 \Rightarrow M\left( 1;1;2 \right)\).
Véc tơ pháp tuyến của mặt phẳng \(\left( P \right)\) là \(\overrightarrow{n}=\left( 1;-2;-1 \right)\)
Véc tơ chỉ phương của đường thẳng \(\Delta \) là \(\overrightarrow{u}=\left( 1;2;1 \right)\)
Đường thẳng d nằm trong mặt phẳng \(\left( P \right)\) đồng thời cắt và vuông góc với \(\Delta \)
Do vậy đường thẳng d nhận \(\frac{1}{2}\left[ \overrightarrow{n},\overrightarrow{u} \right]=\left( 0;-1;2 \right)\) làm véc tơ chỉ phương, mặt khác \(M\left( 1;1;2 \right)\in d\) nên phương trình đường thẳng \(d:\left\{ \begin{array}{l} x = 1\\ y = 1 - t\\ z = 2 + 2t \end{array} \right.\)
Cho f(x) là hàm số bậc bốn thỏa mãn f(0)=0. Hàm số \({{f}^{\prime }}(x)\) có bảng biến thiên như sau:
Hàmsố \(g(x)=\left| f\left( {{x}^{3}} \right)-2021x \right|\) có bao nhiêu điểm cực trị?
Xét hàm số \(y=f\left( {{x}^{3}} \right)-2021x=h\left( x \right)\)
\(h'\left( x \right)=3{{x}^{2}}.f'\left( {{x}^{3}} \right)-2021=0\)
\(\Leftrightarrow f'\left( {{x}^{3}} \right)=\frac{2021}{3{{x}^{2}}}\,\,\left( * \right)\) (Chỉ xét \(x\ne 0\) do x=0 không là nghiệm của phương trình)
Đặt \({{x}^{3}}=u\Rightarrow {{x}^{2}}=\sqrt[3]{{{u}^{2}}}\). \(\left( * \right)\) trở thành \(f'\left( u \right)=\frac{2021}{3\sqrt[3]{{{u}^{2}}}}\)
Số nghiệm của phương trình \(\left( * \right)\) chính là số giao điểm của ĐTHS \(y=f'\left( u \right)\) và \(y=\frac{2021}{3\sqrt[3]{{{\mathsf{u}}^{2}}}}\)
Xét hàm số \(y=t\left( u \right)=\frac{2021}{3\sqrt[3]{{{u}^{2}}}}\Rightarrow t'\left( u \right)=-\frac{4042}{9}.\frac{1}{\sqrt[3]{{{u}^{5}}}}\). Ta có BBT:
⇒ Ta có ĐTHS \(y=f'\left( u \right)\) và \(y=\frac{2021}{3\sqrt[3]{{{u}^{2}}}}\) như sau:
Dựa vào ĐTHS, ta thấy đồ thị hàm \(y=f'\left( u \right)\) và đồ thị hàm \(y=\frac{2021}{3\sqrt[3]{{{u}^{2}}}}\) có 1 giao điểm có hoành độ là a
⇒ Phương trình \(f'\left( u \right)=\frac{2021}{3\sqrt[3]{{{u}^{2}}}}\) có 1 nghiệm u=a>0
⇒ Phương trình \(\left( * \right)\) có 1 nghiệm \(x=\sqrt[3]{a}\)
⇒ Phương trình \(h'\left( x \right)=0\) có 1 nghiệm \(x=\sqrt[3]{a}\)
Ta có BBT của hàm số \(h\left( x \right)\)
(Giải thích \(\left( 1 \right) h\left( 0 \right)=f\left( 0 \right)-0=0\))
Từ BBT của hàm số \(y=h\left( x \right)\),ta thu được BBT của hàm số \(y=g\left( x \right)=\left| h\left( x \right) \right|\)
⇒ Hàm \(g\left( x \right)\) có 3 cực trị
Có bao nhiêu số nguyên y để tồn tại số thực x thỏa mãn \({\log _3}\left( {x + 2y} \right) = {\log _2}\left( {{x^2} + {y^2}} \right)\)
Đặt \({\log _3}\left( {x + 2y} \right) = {\log _2}\left( {{x^2} + {y^2}} \right) = t \Leftrightarrow \left\{ \begin{array}{l} x + 2y = {3^t}\\ {x^2} + {y^2} = {2^t} \end{array} \right.\) (*)
Ta có \({\left( {x + 2y} \right)^2} \le \left( {1 + 4} \right)\left( {{x^2} + {y^2}} \right) = 5\left( {{x^2} + {y^2}} \right)\) nên: \({9^t} \le {5.2^t} \Leftrightarrow {\left( {\frac{9}{2}} \right)^t} \le 5 \Leftrightarrow t \le {\log _{\frac{9}{2}}}5\).
Suy ra \({x^2} + {y^2} = {2^t} \le {2^{{{\log }_{\frac{9}{2}}}5}} \approx 2.1\).
Vì y là số nguyên nên \(y \in \left\{ { - 1;0;1} \right\}\).
+Với y = -1, hệ (*) trở thành \(\left\{ \begin{array}{l} x - 2 = {3^t}\\ {x^2} + 1 = {2^t} \end{array} \right. \Rightarrow {\left( {{3^t} + 2} \right)^2} + 1 = {2^t} \Leftrightarrow {9^t} + {4.3^t} - {2^t} + 5 = 0\) (**)
Nếu t<0 thì \(2-{{2}^{t}}>0\Rightarrow {{9}^{t}}+{{4.3}^{t}}-{{2}^{t}}+5>0\).
Nếu \(t\ge 0\Rightarrow {{9}^{t}}-{{2}^{t}}\ge 0\Rightarrow {{9}^{t}}+{{4.3}^{t}}-{{2}^{t}}+5>0\).
Vậy (**) vô nghiệm.
-Với y = 0 thì hệ (*) trở thành \(\left\{ \begin{array}{l} x = {3^t}\\ {x^2} = {2^t} \end{array} \right. \Rightarrow {9^t} = {2^t} \Leftrightarrow {\left( {\frac{9}{2}} \right)^t} = 1 \Leftrightarrow t = 0 \Rightarrow x = 1\).
-Với y = 1 thì hệ (*) trở thành \(\left\{ \begin{array}{l} x + 2 = {3^t}\\ {x^2} + 1 = {2^t} \end{array} \right. \Rightarrow {\left( {{3^t} - 2} \right)^2} = {2^t} - 1\,\,\left( {***} \right)\).
Dễ thấy (***) luôn có ít nhất một nghiệm \(t = 0 \Rightarrow x = 0\).
Vậy có 2 giá trị nguyên của thỏa mãn là y = 0,y = 1.
Cho hàm số \(y={{x}^{4}}-3{{x}^{2}}+m\) có đồ thị \(\left( {{C}_{m}} \right)\),với m là tham số thực.Giả sử \(\left( {{C}_{m}} \right)\) cắt trục Ox tại bốn điểm phân biệt như hình vẽ
Gọi \({{S}_{1}},{{S}_{2}},{{S}_{3}}\) là diện tích các miền gạch chéo được cho trên hình vẽ. Giá trị của m để \({{S}_{1}}+{{S}_{3}}={{S}_{2}}\) là
Gọi \({{x}_{1}}\) là nghiệm dương lớn nhất của phương trình \({{x}^{4}}-3{{x}^{2}}+m=0\),ta có \(m=-x_{1}^{4}+3x_{1}^{2} \left( 1 \right)\).
Vì \({{S}_{1}}+{{S}_{3}}={{S}_{2}}\) và \({{S}_{1}}={{S}_{3}}\) nên \({{S}_{2}}=2{{S}_{3}}\) hay \(\int\limits_{0}^{{{x}_{1}}}{f\left( x \right)\text{d}x}=0\).
Mà \(\int\limits_{0}^{{{x}_{1}}}{f\left( x \right)\text{d}x} =\int\limits_{0}^{{{x}_{1}}}{\left( {{x}^{4}}-3{{x}^{2}}+m \right)\text{d}x} =\left. \left( \frac{{{x}^{5}}}{5}-{{x}^{3}}+mx \right) \right|_{0}^{{{x}_{1}}} =\frac{x_{1}^{5}}{5}-x_{1}^{3}+m{{x}_{1}} ={{x}_{1}}\left( \frac{x_{1}^{4}}{5}-x_{1}^{2}+m \right)\).
Dođó,\({{x}_{1}}\left( \frac{x_{1}^{4}}{5}-x_{1}^{2}+m \right)=0 \Leftrightarrow \frac{x_{1}^{4}}{5}-x_{1}^{2}+m=0 \left( 2 \right)\).
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\), ta có phương trình \(\frac{x_{1}^{4}}{5}-x_{1}^{2}-x_{1}^{4}+3x_{1}^{2}=0 \Leftrightarrow -4x_{1}^{4}+10x_{1}^{2}=0 \Leftrightarrow x_{1}^{2}=\frac{5}{2}\).
Vậy \(m=-x_{1}^{4}+3x_{1}^{2} =\frac{5}{4}\).
Cho hai số phức \({{z}_{1}},{{z}_{2}}\) thỏa mãn \(\left| {{z}_{1}}-5+3i \right|=\left| {{z}_{1}}-1-3i \right|,\left| {{z}_{2}}-4-3i \right|=\left| {{z}_{2}}-2+3i \right|\). Giá trị nhỏ nhất của biểu thức \(P=\left| {{z}_{1}}-{{z}_{2}} \right|+\left| \overline{{{z}_{1}}}-6+i \right|+\left| {{z}_{2}}-6-i \right|\) là
Đặt \({{z}_{1}}=x+yi\) thì \(\left| {{z}_{1}}-5+3i \right|=\left| {{z}_{1}}-1-3i \right|\Leftrightarrow 2\text{x}-3y-6=0\left( {{d}_{1}} \right).\)
Đặt \({{z}_{2}}=x'+y'i\) thì \(\left| {{z}_{2}}-4-3i \right|=\left| {{z}_{2}}-2+3i \right|\Leftrightarrow \text{x }\!\!'\!\!\text{ +3}y'-3=0\left( {{d}_{2}} \right).\)
Gọi A,B lần lượt là điểm biểu diễn của \({{z}_{1}},{{z}_{2}}\) thì \(A\in {{d}_{1}};B\in {{d}_{2}}.\)
Gọi \(C\left( 6;1 \right)\).
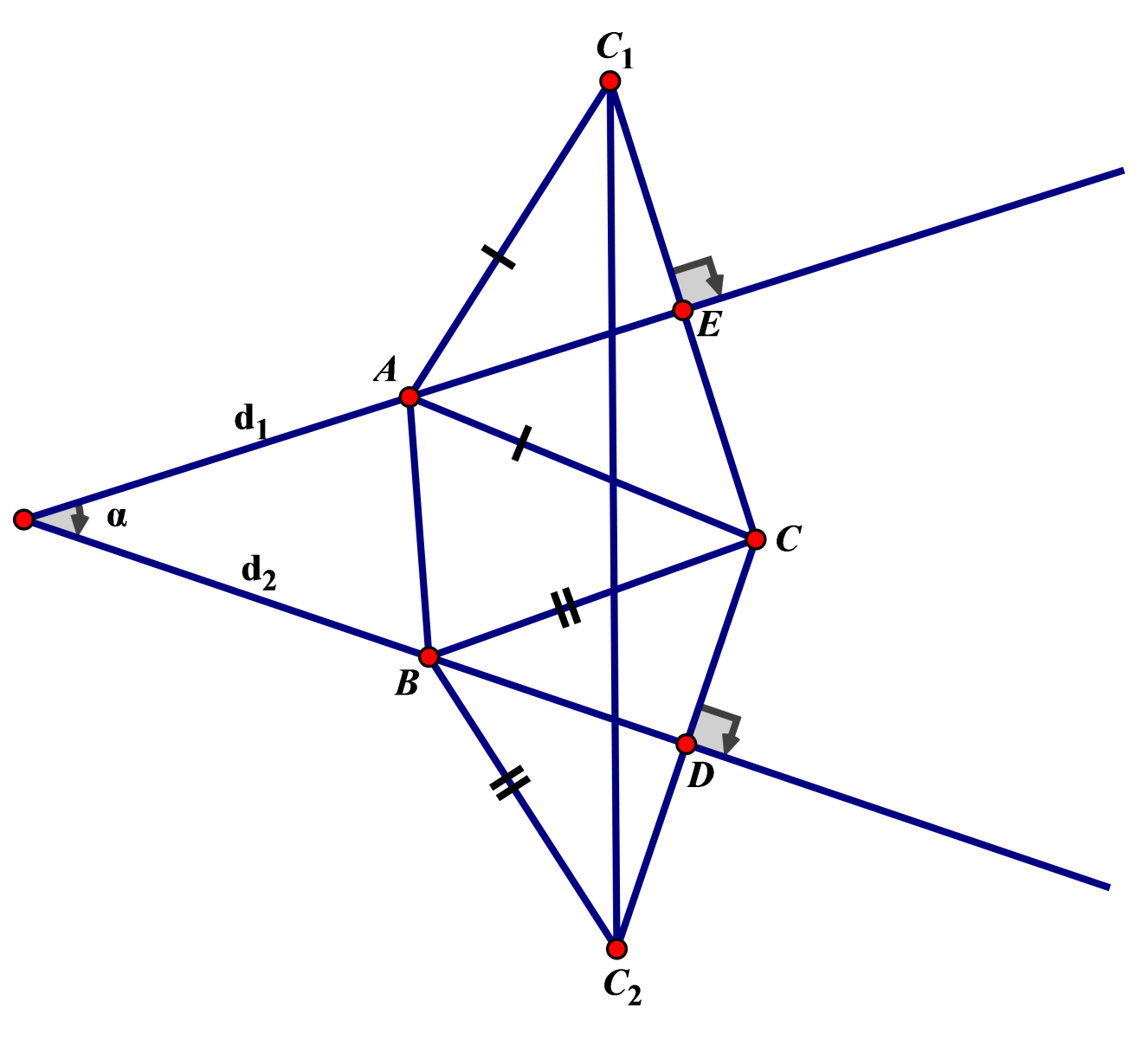
\(\begin{align} & P=\left| {{z}_{1}}-{{z}_{2}} \right|+\left| \overline{{{z}_{1}}}-6+i \right|+\left| {{z}_{2}}-6-i \right| \\ & =\left| {{z}_{1}}-{{z}_{2}} \right|+\left| {{z}_{1}}-6-i \right|+\left| {{z}_{2}}-6-i \right|. \\ & =AB+AC+BC\ge {{C}_{1}}{{C}_{2}}. \\ \end{align}\)
Với \({{C}_{1}},{{C}_{2}}\) lần lượt đối xứng với C qua \({{d}_{1}};{{d}_{2}}.\)
Phương trình \(C{{C}_{1}}:3x+2y-20=0\Rightarrow {{C}_{1}}\left( \frac{66}{13};\frac{31}{13} \right)\)
Phương trình \(C{{C}_{2}}:3x-y-17=0\Rightarrow {{C}_{2}}\left( \frac{24}{5};\frac{-13}{5} \right)\)
Vậy \({{C}_{1}}{{C}_{2}}=\frac{18}{\sqrt{13}}.\)
Trong không gian với hệ tọa độ Oxyz,cho mặt phẳng \(\left( P \right):x+y+z-1=0\), đường thẳng \(\left( d \right):\frac{x-15}{1}=\frac{y-22}{2}=\frac{z-37}{2}\) và mặt cầu \(\left( S \right):{{x}^{2}}+{{y}^{2}}+{{z}^{2}}-8x-6y+4z+4=0\).Một đường thẳng \(\left( \Delta \right)\) thay đổi cắt mặt cầu \(\left( S \right)\) tại hai điểm A,B sao cho AB=8. Gọi \({A}', {B}'\) là hai điểm lần lượt thuộc mặt phẳng \(\left( P \right)\) sao cho \(A{A}',B{B}'\) cùng song song với \(\left( d \right)\).Giá trị lớn nhất của biểu thức \(A{A}'+B{B}'\) là
Mặt cầu \(\left( S \right)\) có tâm \(I\left( 4;3;-2 \right)\) và bán kính R=5.
Gọi H là trung điểm của AB thì \(IH\bot AB\) và IH=3 nên H thuộc mặt cầu \(\left( {{S}'} \right)\) tâm I bánkính \({R}'=3\)
Gọi M là trung điểm của \({A}'{B}'\) thì \(A{A}'+B{B}'=2HM\), M nằm trên mặt phẳng \(\left( P \right)\).
Mặt khác ta có \(d\left( I;\left( P \right) \right)=\frac{4}{\sqrt{3}}<R\) nên \(\left( P \right)\) cắt mặt cầu \(\left( S \right)\) và \(\sin \left( d;\left( P \right) \right)=\sin \alpha =\frac{5}{3\sqrt{3}}\). Gọi K là hình chiếu của H lên \(\left( P \right)\) thì \(HK=HM.\sin \alpha \).
Vậy để \(A{A}'+B{B}'\) lớn nhất thì HK lớn nhất
\(\Leftrightarrow HK\) đi qua I nên \(H{{K}_{\max }}={R}'+d\left( I;\left( P \right) \right)=3+\frac{4}{\sqrt{3}}=\frac{4+3\sqrt{3}}{\sqrt{3}}\).
Vậy \(A{A}'+B{B}'\) lớn nhất bằng \(2\left( \frac{4+3\sqrt{3}}{\sqrt{3}} \right).\frac{3\sqrt{3}}{5}=\frac{24+18\sqrt{3}}{5}\).

.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)



