- Đoạn mạch chỉ có điện trở: u cùng pha i. 

- Đoạn mạch chỉ có cuộn dây thuần cảm: u nhanh pha hơn i góc π/2. 

- Đoạn mạch chỉ có cuộn dây không thuần cảm: u nhanh pha hơn i một góc nhỏ hơn π/2.

- Đoạn mạch chỉ có tụ: u chậm pha hơn i góc π/2. 

Ca sĩ “lên tone” khi hát nghĩa là điều chỉnh giọng hát ở các nốt cao → liên quan đến đặc trưng sinh lý là độ cao của âm ứng với đặc trưng vật lý là tần số âm. 

Khi vật dao động điều hòa thì tần số không thay đổi theo thời gian. 

Mạng điện xoay chiều dân dụng của Việt Nam có tần số là \(f=50~\text{Hz}\)

Ta có: \(E=\frac{1}{2}mgl\alpha _{0}^{2}\)

Vận tốc được tính theo công thức: v=λ/T

Phần cảm có tác dụng tạo ra từ trường, phần ứng là nơi xuất hiện suất điện động cảm ứng. 

Biên độ của dao động tổng hợp đạt giá trị nhỏ nhất bằng |A₁ − A₂| khi hai dao động thành phần ngược pha nhau. 

Công của lực điện trường khi làm điện tích q di chuyển từ M đến \(\text{N}:{{\text{A}}_{\text{MN}}}=\text{q}{{\text{U}}_{\text{MN}}}=-{{6.10}^{-4}}~\text{J}\).

Khoảng cách giữa 4 nút sóng liên tiếp: \(\frac{3\lambda }{2}=60\Rightarrow \lambda =40~\text{cm}\).

Vận tốc truyền sóng: \(v=\lambda f=400~\text{cm}/\text{s}\). 

Sóng âm bao gồm hạ âm (tần số dưới 16 Hz), âm nghe được (tần số từ 16 đến 20000 Hz) và siêu âm (tần số trên 20000 Hz). 

5 ngọn sóng nước đi qua trước mặt mình trong thời gian \(10~\text{s}\Rightarrow 4~\text{T}=10~\text{s}\Rightarrow \text{T}=2,5~\text{s}\)

Các giá trị hiệu dụng không thể cộng lại mà phải tính theo biểu thức \(\text{U}=\sqrt{\text{U}_{\text{R}}^{2}+\text{U}_{\text{C}}^{2}}\) (hoặc vì u_R vuông pha với u_C nên không dùng được hệ thức ở đáp án D) 

Chu kỳ dao động điều hoà của con lắc lò xo:

\(\text{T}=2\pi \sqrt{\frac{m}{k}}\to \text{T}\sim\sqrt{m}\Rightarrow \frac{{{T}_{2}}}{{{T}_{1}}}=\frac{\sqrt{{{m}_{2}}}}{\sqrt{{{m}_{1}}}}\Rightarrow {{T}_{2}}=2\sqrt{2}\)

400 V là hiệu điện thế giới hạn của tụ. Nếu vượt quá giá trị này thì tụ sẽ bị hỏng (điện môi sẽ bị đánh thủng) 

Trong giao thoa sóng thì khoảng cách giữa hai điểm cực đại (hoặc 2 điểm cực tiểu) liên tiếp trên đoạn thẳng nối  2 nguồn sóng là nửa bước sóng. Hs không cẩn thận chọn B sẽ sai vì đề bài không viết “liên tiếp” hay “gần nhau nhất” → có thể là hai điểm cực đại (hoặc 2 điểm cực tiểu) bất kỳ, không liên tiếp thì cách nhau một số nguyên lần nửa bước sóng.  

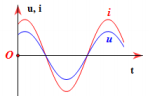
Dễ dạng nhận thấy được từ đồ thị → u và i cùng pha → Mạch chỉ có R. 

Ta có \(\frac{\text{PR}}{{{\text{U}}^{2}}{{\cos }^{2}}\varphi }=1-\text{H}\Rightarrow \text{R}=(1-\text{H})\cdot \frac{{{\text{U}}^{2}}{{\cos }^{2}}\varphi }{\text{P}}=(1-0,95)\cdot \frac{{{\left( {{500.10}^{3}} \right)}^{2}}}{{{10}^{6}}}=12,5\text{k}\Omega \)

Nhạc cụ này có thể phát ra các họa âm bậc n là: \(\text{n}{{f}_{0}}(\text{n}=1,2,3\ldots )\)

⇒ Tần số lớn nhất nhạc cụ có thể phát ra để người đó nghe được là \(42{{f}_{0}}.\)

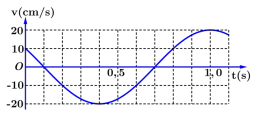
+ Từ đồ thị ta có: \(\frac{T}{12}+\frac{T}{2}+\frac{T}{4}=1\Rightarrow T=1,2s\Rightarrow \omega =\frac{5\pi }{3}\text{ rad }/\text{s};{{v}_{\max }}=20\frac{\text{cm}}{\text{s}}=\text{A}\omega \Rightarrow A=\frac{12}{\pi }\text{cm}\)

+ Tại \(\text{t}=0\Rightarrow {{v}_{0}}=10=20\cos {{\varphi }_{V}}\Rightarrow {{\varphi }_{V}}=\pm \frac{\pi }{3}\xrightarrow{v\downarrow }{{\varphi }_{V}}=+\frac{\pi }{3}\Rightarrow \varphi ={{\varphi }_{V}}-\frac{\pi }{2}=-\frac{\pi }{6}\)

Vậy pt dao động là: \(x=\frac{12}{\pi }\cos \left( \frac{5\pi }{3}t-\frac{\pi }{6} \right)(\text{cm})\)

Khi xảy ra hiện tượng cộng hưởng thì tần số dao động cưỡng bức bằng tần số dao động riêng của hệ lúc này  biên độ của dao động cưỡng bức là lớn nhất. 

Cơ năng \(\text{W}=\frac{1}{2}\text{k}{{\text{A}}^{2}}=\frac{1}{2}\cdot 100.0,{{1}^{2}}=0,5~\text{J}\)

Khi \(t=0\) thì \(i=\frac{{{I}_{0}}}{2}\) và đang giảm \(\to \text{i}=-{{\text{I}}_{0}}\) lần đầu tiên tại thời điểm \(\text{t}=\frac{\text{T}}{12}+\frac{\text{T}}{4}=\frac{\text{T}}{3}=\frac{2\pi }{100\pi }\cdot \frac{1}{3}=\frac{1}{150}~\text{S}\).

Ta có:

\(\text{F}=\text{k}\frac{\left| {{q}_{1}}{{q}_{2}} \right|}{{{r}^{2}}}\Rightarrow \frac{{{F}_{2}}}{{{F}_{1}}}={{\left( \frac{{{r}_{1}}}{{{r}_{2}}} \right)}^{2}}\Rightarrow \frac{{{5.10}^{-7}}}{{{20.10}^{-7}}}={{\left( \frac{d}{d+10} \right)}^{2}}\Rightarrow d=10~\text{cm}\)

Ta có \(\text{MN}=3\lambda =60\Rightarrow \lambda =20~\text{cm}\)

Tốc độ truyền sóng: \(v=\lambda f=200~\text{cm}/\text{s}\)

+ Khi chỉ mắc R hoặc L hoặc C vào nguồn U thì: 

\(\left\{ \begin{array}{*{35}{l}} \text{R}=\frac{\text{U}}{{{\text{I}}_{\text{R}}}}=\frac{\text{U}}{2} \\ {{\text{Z}}_{\text{L}}}=\frac{\text{U}}{{{\text{I}}_{\text{L}}}}=\text{U} \\ {{\text{Z}}_{\text{C}}}=\frac{\text{U}}{{{\text{I}}_{\text{C}}}}=\frac{\text{U}}{3} \\ \end{array} \right.\)

+ Khi mắc R, L, C nối tiếp: \(\text{Z}=\sqrt{{{\text{R}}^{2}}+{{\left( {{\text{Z}}_{\text{L}}}-{{\text{Z}}_{\text{C}}} \right)}^{2}}}=\sqrt{\frac{{{\text{U}}^{2}}}{4}+{{\left( \text{U}-\frac{\text{U}}{3} \right)}^{2}}}=\frac{5}{6}\text{U}\)

+ Cường độ dòng điện hiệu dụng lúc này là: \({{\text{I}}_{\text{RLC}}}=\frac{\text{U}}{\text{z}}=\frac{6}{5}=1,2~\text{A}\)

Ta có: 

\(\frac{{{\text{N}}_{2}}}{~{{\text{N}}_{1}}}=3=\frac{{{\text{U}}_{2}}}{{{\text{U}}_{1}}}=\frac{{{\text{I}}_{1}}}{{{\text{I}}_{2}}}\Rightarrow \left\{ \begin{array}{*{35}{l}} {{\text{U}}_{2}}=3.{{\text{U}}_{1}}=3.360=1080~\text{V} \\ {{\text{I}}_{2}}=\frac{{{\text{I}}_{1}}}{3}=2~\text{A} \\ \end{array} \right.\)

Mạch chỉ có cuộn cảm thuần ⇒ u vuông pha \(i\Rightarrow \frac{{{u}^{2}}}{{{U}^{2}}}+\frac{{{i}^{2}}}{{{I}^{2}}}=2\).

Do đó: khi \(\text{i}=\frac{1}{2}\text{ th }\!\!\grave{\mathrm{i}}\!\!\text{  }\frac{{{\text{u}}^{2}}}{{{\text{U}}^{2}}}+\frac{1}{4}=2\Rightarrow \text{u}=\frac{\text{U}\sqrt{7}}{2}=50\sqrt{7}~\text{V}\)

Sử dụng công thức tính biên độ dao động tổng hợp:

\(\text{A}=\sqrt{\text{A}_{1}^{2}+\text{A}_{1}^{2}+2\cdot {{\text{A}}_{1}}\cdot {{\text{A}}_{2}}\cos \left( {{\varphi }_{2}}-{{\varphi }_{1}} \right)}=4\sqrt{3}~\text{cm}\)

Tốc độ cực đại của vật trong qua trình dao động: \({{\text{v}}_{\max }}=\omega \text{A}=4\pi \sqrt{3}~\text{cm}/\text{s}\)

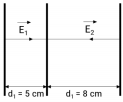
Gốc điện thế tại bản A: V_A = 0. 

U_AB = E₁. d₁ = V_A − V_B → V_B = V_A − E₁d₁ = 0 − 4.10⁴. 0,05 = −2000 V/m.

U_CB = E₂. d₂ = V_C − V_B → V_C = V_B + E₂d₂ = −2000 + 5.10⁴. 0,08 = 2000 V/m.

Quay một vòng đi qua li độ \(x=2\sqrt{3}~\text{cm}\) là hai lần. 

Để có lần thứ 2012 = 2.1005 + 2 thì phải quay 1005 vòng và quay thêm một góc  

4π/3, tức là tổng góc quay: \(\Delta \varphi =1005.2\pi +4\pi /3\)

 Thời gian: \(t=\frac{\Delta \varphi }{\omega }=\frac{1005.2\pi +\frac{4\pi }{3}}{\frac{4\pi }{3}}=1508,5(s)\)

Khoảng cách giữa 3 nút liên tiếp: \(\overline{d}=20cm=\overline{\lambda }\).

Vận tốc truyền sóng \(\overline{\text{v}}=\bar{\lambda }\cdot \overline{\text{f}}=20000~\text{cm}/\text{s}\).

Sai số tương đối: \(\frac{\Delta v}{{\bar{v}}}=\frac{\Delta \lambda }{{\bar{\lambda }}}+\frac{\Delta f}{{\bar{f}}}={{6.10}^{-3}}\Rightarrow \Delta v=0,6%\).

Biễu diễn vector các dao động. Từ hình vẽ, ta có: 

o \(\widehat{OAB}={{\varphi }_{1}}-\varphi =\frac{\pi }{4}\). (2 góc so le trong)

o \(\frac{OB}{\sin \widehat{OAB}}=\frac{AB}{\sin \left( \varphi +{{15}^{0}} \right)}\to \sin \left( \varphi +{{15}^{0}} \right)=\frac{AB}{OB}\sin \widehat{OAB}=\frac{(6)}{(2\sqrt{6})}\sin \left( {{45}^{0}} \right)=\frac{\sqrt{3}}{2}\).

\(\to \varphi ={{60}^{0}}-{{15}^{0}}={{45}^{0}}\text{ v }\!\!\grave{\mathrm{a}}\!\!\text{  }{{\varphi }_{1}}={{90}^{0}}\to \frac{\varphi }{{{\varphi }_{1}}}=\frac{1}{2}\).

- Từ đồ thị ta thấy: Y là cuộn cảm, Z là điện trở, X là tụ điện.

- Khi \(f={{f}_{1}}\) thì R = Z_C1 

- Khi \(f={{f}_{1}}\) thì \({{\text{Z}}_{\text{L}2}}={{\text{Z}}_{\text{C}2}}=\frac{{{\text{z}}_{\text{C}1}}}{2}=\frac{\text{R}}{2};{{\text{Z}}_{\text{L}2}}=2{{\text{Z}}_{\text{L}1}}\Rightarrow {{\text{Z}}_{\text{L}1}}=\frac{\text{R}}{4}\)

- Khi \(f={{f}_{1}}\) thì \(\cos \varphi =\frac{\text{R}}{\sqrt{{{\text{R}}^{2}}+{{\left( {{\text{Z}}_{\text{L}1}}-{{\text{Z}}_{\text{C}1}} \right)}^{2}}}}=0,8\Rightarrow {{\text{I}}_{1}}=\frac{{{\text{P}}_{1}}}{\text{U}\cos {{\varphi }_{1}}}=1~\text{A}\Rightarrow \text{R}=\frac{{{\text{P}}_{1}}}{\text{I}_{1}^{2}}=160\Omega ={{\text{Z}}_{\text{C}1}}\)

\(\Rightarrow {{Z}_{L1}}=\frac{R}{4}=40\Omega \)

+ Theo đề ta có: 

\( \left\{ \begin{array}{*{35}{l}} {{P}_{M}}={{P}_{10}}={{P}_{0}}\cdot {{(0,97)}^{5}} \\ {{P}_{N}}={{P}_{110}}={{P}_{0}}\cdot {{(0,97)}^{55}} \\ \end{array} \right.\)

\(\Rightarrow \left\{ \begin{array}{*{35}{l}} {{I}_{M}}=\frac{{{P}_{M}}}{4\pi R_{M}^{2}}=\frac{{{P}_{0}}\cdot {{(0,97)}^{5}}}{4\pi {{10}^{2}}} \\ {{I}_{N}}=\frac{{{P}_{N}}}{4\pi R_{N}^{2}}=\frac{{{P}_{0}}\cdot {{(0,97)}^{55}}}{4\pi {{110}^{2}}} \\ \end{array}\Rightarrow \frac{{{I}_{N}}}{{{I}_{M}}}=\frac{{{(0,97)}^{55}}\cdot {{10}^{2}}}{{{(0,97)}^{5}}\cdot {{110}^{2}}}=1,{{802.10}^{-3}} \right.\)

+ Vậy \({{L}_{N}}-{{L}_{M}}=10\log \frac{{{I}_{N}}}{{{I}_{M}}}\Rightarrow {{L}_{N}}={{L}_{M}}+10\log \frac{{{I}_{N}}}{{{I}_{M}}}=60+10\log \left( 1,{{802.10}^{-3}} \right)=32,56dB\)

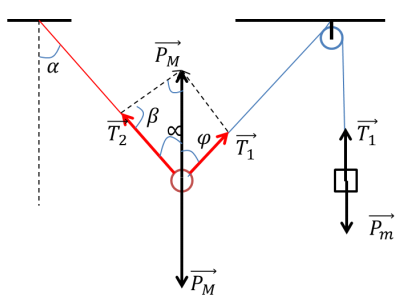
Từ hình vẽ ta có: \(\beta ={{135}^{0}}-\frac{\alpha }{2}\)

Áp dụng định lý hàm số sin ta có: 

\(\frac{{{T}_{1}}}{\sin \alpha }=\frac{{{P}_{M}}}{\sin \beta }\leftrightarrow \frac{{{P}_{m}}}{\sin \alpha }=\frac{{{P}_{M}}}{\sin \left( {{135}^{0}}-\frac{\alpha }{2} \right)}\to \alpha =10,{{16}^{0}}\)

Khi ta đốt sợi dây con lắc đơn M sẽ dao động với biên độ góc \(\alpha ={{\alpha }_{0}}=10,{{16}^{0}}\)

Vận tốc khi M qua vị trí cân bằng 

\(v=\sqrt{2g\ell \left( 1-\cos {{\alpha }_{0}} \right)}=39,2~\text{cm}/\text{s}\)

Gọi điện áp nơi phát điện, nơi tiêu thụ, độ giảm áp, cường độ dòng điện lúc đầu lần lượt là: \({{U}_{01}};{{U}_{1}};\Delta {{U}_{1}};{{I}_{1}}\)

Và lúc sau là: \({{U}_{02}};{{U}_{2}};\Delta {{U}_{2}};{{I}_{2}}\)

Ta có công suất hao phí: \(\Delta P=R{{I}^{2}}\), R không đổi nên hao phí giảm 81 lần thì cường độ dòng điện giảm đi 9  lần. 

Nên 

\(\begin{array}{l}
\frac{{{I_2}}}{{{I_1}}} = \frac{1}{9}\\
 \Rightarrow \left\{ {\begin{array}{*{20}{l}}
{\frac{{{U_2}}}{{{U_1}}} = 9{\rm{ (c }}\widehat {\rm{o}}{\rm{ ng suat ti }}\widehat {\rm{e}}{\rm{ u thu }}\left. {{P_{tt2}} = {P_{tt1}} \leftrightarrow {U_2}{I_2} = {U_1}{I_1}} \right)}\\
{\frac{{\Delta {U_2}}}{{A{I_2}}} = \frac{1}{9}({\rm{ d }}\widehat {\rm{o}}{\rm{  giam the }}\Delta U = R.I{\rm{ m }}\mathop {\rm{a}}\limits^` {\rm{  }}R{\rm{ kh }}\widehat {\rm{o}}{\rm{ ng doi}})}
\end{array}} \right.\\
{U_{02}} = {U_2} + \Delta {U_2} = 9{U_1} + \frac{{\Delta {U_1}}}{9} = 9{U_1} + \frac{{0,1{U_1}}}{9} \simeq 9,011{U_1}
\end{array}\)

Trong đề gọi điện áp nơi tiêu thụ là U nên đáp án là B. 

Ta có: \(\frac{\lambda }{2}<24-22,5\le \lambda \to 2,5~\text{cm}\le \lambda <5~\text{cm}.\)

Vì số giao thoa cực đại trên AB là số lẻ nên: \(21,5=k\lambda \to 5\le k\le 8\)

\(\to f=\frac{v}{\lambda }=\frac{25}{21,5}k=\frac{50}{43}k\xrightarrow{{{k}_{\min }}=5}{{f}_{\min }}=5,81Hz\)

Xét đồ thị tại \(t=0\)

\({u_{RL}}\left\{ {\begin{array}{*{20}{c}}
{{U_{0RL}} = \sqrt 6  \cdot x}\\
{{\varphi _{uRL}} = 0}
\end{array}} \right.{u_{RC}}\left\{ {\begin{array}{*{20}{c}}
{{U_{0RC}} = 2x}\\
{{\varphi _{uRC}} =  - \frac{{5\pi }}{{12}}}
\end{array}} \right.\)

Dựa trên giản đồ vector Fresnel :  

+ Định lý hàm cos: \({{\left( {{U}_{L}}+{{U}_{C}} \right)}^{2}}=U_{RL}^{2}+U_{RC}^{2}-2{{U}_{RL}}{{U}_{RC}}\cos \left( \frac{5\pi }{12} \right)\)

\(\Rightarrow {{\text{U}}_{\text{L}}}+{{\text{U}}_{\text{C}}}=\sqrt{4+2\sqrt{3}}\)

\(+\text{S}=\frac{1}{2}*\sqrt{6}*2*\sin \left( \frac{5\pi }{12} \right)=\frac{1}{2}*{{\text{U}}_{\text{R}}}\left( {{\text{U}}_{\text{L}}}+{{\text{U}}_{\text{C}}} \right)\)

\(\Rightarrow {{\text{U}}_{\text{R}}}=\sqrt{3},{{\text{U}}_{\text{L}}}=\sqrt{3},{{\text{U}}_{\text{C}}}=1\)

\(\Rightarrow {{Z}_{L}}=\text{R},{{Z}_{C}}=\frac{\text{R}}{\sqrt{3}}\Rightarrow {{Z}_{L}}{{Z}_{C}}=\frac{{{\text{R}}^{2}}}{\sqrt{3}}\Rightarrow \frac{{{\text{R}}^{2}}\text{C}}{2~\text{L}}=\frac{\sqrt{3}}{2}\)

+ Khi \({{\omega }_{2}}\) thì \({{\text{U}}_{\text{cmax}}}\Rightarrow {{\left( \frac{\text{U}}{{{\text{U}}_{\text{Cmax}}}} \right)}^{2}}=1-{{\left( 1-\frac{{{\text{R}}^{2}}\text{C}}{2~\text{L}} \right)}^{2}}\Rightarrow {{\text{U}}_{\text{cmax}}}=\frac{\text{U}}{\sqrt{1-{{\left( 1-\frac{{{\text{R}}^{2}}\text{C}}{2~\text{L}} \right)}^{2}}}}=50,45(~\text{V})\)

+ Vì \({{\text{a}}_{\text{max}}}={{\omega }^{2}}~\text{A}=\left( \frac{\text{k}}{\text{M}+\text{m}} \right)\text{A}=\frac{50.0,05}{0,4+0,05}=5,56\left( ~\text{m}/{{\text{s}}^{2}} \right)<\text{g}=10\left( ~\text{m}/{{\text{s}}^{2}} \right)\Rightarrow \)vật m cùng dao động với M 

+ Các lực tác dụng lên m gồm: trọng lực \({{\overrightarrow{P}}_{m}}\), phản lực \(\overrightarrow{N}\)

+ Theo định luật II Niu-tơn ta có: \({{\overrightarrow{\text{P}}}_{\text{m}}}+\overrightarrow{\text{N}}=\text{m}\overrightarrow{\text{a}}\)

+ Chiếu lên chiều dương (hướng xuống) ta có: \({{P}_{m}}-N=ma\)

Do vật ở trên vị trí cân bằng 4,5 cm:  

\(\Rightarrow N={{P}_{m}}-ma=m(g-a)=m\left( g+{{\omega }^{2}}x \right)\)