Đề thi thử THPT QG năm 2021 môn Vật Lý - Trường THPT Thái Đào
Đề thi thử THPT QG năm 2021 môn Vật Lý
-
Hocon247
-
40 câu hỏi
-
90 phút
-
48 lượt thi
-
Dễ
Tham gia [ Hs Hocon247.com ] - Cộng Đồng Luyện Thi Trực Tuyến để được học tập những kiến thức bổ ích từ HocOn247.com
Hai điện tích điểm mang điện tích q1>0; q2<0; \(\left| {{q}_{1}} \right|>\left| {{q}_{2}} \right|\). Cho chúng tiếp xúc nhau rồi tách ra. Điện tích của mỗi điện tích điểm sau đó là …
Điện tích của mỗi điện tích điểm sau đó là: \(\frac{{{q}_{1}}+{{q}_{2}}}{2}\).
Hai điện tích điểm q1= 2mC và q2 = 8mC đặt tại hai điểm A và B cách nhau 12cm trong chân không. Điểm M cách B một khoảng bao nhiêu, để có cường độ điện trường tổng hợp bằng 0.
Ta có:
Ta có: E1 = E2; Do q1 cùng dấu q2.
Nên:
\(\frac{{{q}_{1}}}{{{\left( 12-{{r}_{2}} \right)}^{2}}}=\frac{{{q}_{2}}}{r_{2}^{2}}\Rightarrow \left\{ \begin{align} & {{r}_{2}}=8cm \\ & {{r}_{2}}=24cm \\ \end{align} \right.\)
Cho mạch điện nguồn điện có suất điện động E và điện trở trong r = 2Ω, mạch ngoài có điện trở R = 14Ω và ampe kế chỉ 0,75A. Suất điện động của nguồn là:
Ta có: \(I=\frac{\xi }{R+r}\Rightarrow \xi =12V\)
Cho một mạch điện có điện trở không đổi. Khi dòng điện trong mạch là 2 A thì công suất tiêu thụ của mạch là 100 W. Khi dòng điện trong mạch là 1 A thì công suất tiêu thụ của mạch là
Ta có:
\(\frac{{{P}_{2}}}{{{P}_{1}}}={{\left( \frac{{{I}_{2}}}{{{I}_{1}}} \right)}^{2}}\Rightarrow {{P}_{2}}=25W\)
Độ lớn của lực Lorexơ được tính theo công thức
Độ lớn của lực Lorexơ được tính theo công thức :
\(f=\left| q \right|vB\sin \alpha \)
Gọi α là góc hợp bởi vectơ pháp tuyến \(\overrightarrow{n}\) của diện tích S với vectơ cảm ứng từ \(\overrightarrow{\text{B}}\). Từ thông qua diện tích S có độ lớn cực đại khi α bằng
ừ thông qua diện tích S có độ lớn cực đại khi α bằng 0
Một người cận thị có khoảng nhìn rõ từ 12,5 cm đến 50 cm. Khi đeo kính chữa tật của mắt, người này nhìn rõ được các vật đặt gần nhất cách mắt:
Người cận thị đeo kính để sửa tật có f = -OCv= -50cm;
Vật đặt ở gần nhất cho ảnh ảo ở cực cận của mắt nên d’ = -12,5cm;
Ta có:
\(d=\frac{d'f}{d'-f}=\frac{-12,5.\left( -50 \right)}{-12,5+50}=\frac{50}{3}cm\)
Một vật dao động điều hòa theo phương trình x= 5cos(8πt + π/2) cm . Tần số góc của dao động là
Tần số góc của dao động là 8π rad/s.
Phát biểu nào sau đây là sai khi nói về dao động tắt dần?
Phát biểu sai : Cơ năng của dao động bảo toàn.
Trong dao động điều hòa của chất điểm, vectơ gia tốc và vectơ vận tốc cùng chiều khi chất điểm
Trong dao động điều hòa của chất điểm, vectơ gia tốc và vectơ vận tốc cùng chiều khi chất điểm chuyển động về vị trí cân bằng.
Sóng cơ truyền trên một sợi dây rất dài với khoảng cách giữa hai đỉnh sóng liên tiếp là 20 cm. Bước sóng λ bằng:
Bước sóng λ bằng: 20 cm.
Khi âm thanh truyền từ nước ra không khı́ thì:
Khi âm thanh truyền từ nước ra không khı́ thì bước sóng giảm, tần số không đổi.
Mạch điện xoay chiều RLC mắc nối tiếp đang có tính cảm kháng, khi tăng tần số của dòng điện xoay chiều thì hệ số công suất của mạch là:
Hệ số công suất của mạch giảm.
Một nguyên tử chuyển từ trạng thái dừng năng lượng En = -1,5 eV sang trạng thái dừng năng lượng Em = -3,4 eV. Tần số của bức xạ mà nguyên tử phát ra là
Ta có:
\(f=\frac{{{E}_{n}}-{{E}_{m}}}{h}=\frac{{{1,9.1,6.10}^{-19}}}{{{6.625.10}^{-34}}}\)=4,59.1014Hz
Nguồn sóng ở O dao động với tần số 10Hz, dao động truyền đi với tốc độ v= 0,4m/s theo phương Oy; trên phương này có hai điểm P và Q với PQ = 15cm. Biên độ sóng bằng a = 1cm và không thay đổi khi lan truyền. Nếu tại thời điểm nào đó P có li độ 1cm thì li độ tại Q lúc đó là
Ta có:
\(\lambda =\frac{v}{f}=4cm\);
PQ=15cm = \(3\lambda +\frac{\lambda }{2}+\frac{\lambda }{4}\)
=> P có li độ 1cm (đang ở biên) thì Q qua VTCB
Một bàn ủi (bàn là) điện trên nhãn có ghi AC 220V-240V~ 50Hz – 1000W. Bàn ủi này hoạt động tốt nhất khi mắc vào nguồn xoay chiều có điện áp
Bàn ủi này hoạt động tốt nhất khi mắc vào nguồn xoay chiều có điện áp hiệu dụng từ 220V đến 240V, tần số 50Hz.
Khi sử dụng máy thu thanh vô tuyến, người ta xoay nút dò đài để
Khi sử dụng máy thu thanh vô tuyến, người ta xoay nút dò đài để thay đổi tần số riêng của mạch chọn sóng.
Lõi thép của máy biến áp được cấu tạo từ các lá thép mỏng ghép cách điện
Lõi thép của máy biến áp được cấu tạo từ các lá thép mỏng ghép cách điện để giảm sự nóng lên của máy khi hoạt động.
Trong mạch dao động điện từ, nếu điện tích cực đại trên tụ điện là Q0 và cường độ dòng điện cực đại trong mạch là I0 thì chu kì dao động điện từ trong mạch là
Chu kì dao động điện từ trong mạch là \(T=2\pi \frac{{{Q}_{0}}}{{{I}_{0}}}\)
Trong máy quang phổ lăng kính, lăng kính có tác dụng
Trong máy quang phổ lăng kính, lăng kính có tác dụng tán sắc ánh sáng.
“Theo Thông tư số 10/2009-BGTVT của Bộ Giao thông vận tải, nếu âm lượng của còi xe ô tô điểm cách đầu xe 2m mà lớn hơn 115dB là không đạt tiêu chuẩn an toàn kỹ thuật bảo vệ môi trường”. Lấy cường độ âm chuẩn là Io = 10-12 W/m2. Vậy để đạt tiêu chuẩn này thì công suất của còi xe (xem là nguồn điểm, đặt trước đầu xe) không vượt quá:
Ta có:
\(L=10\lg \frac{I}{{{I}_{0}}}=115\Rightarrow I={{10}^{11,5}}.{{I}_{0}}\);
\(P=4\pi .{{r}^{2}}.I=4\pi .{{r}^{2}}{{.10}^{11,5}}.{{I}_{0}}=15,9W\).
Tổng hợp hạt nhân heli \({}_{\text{2}}^{\text{4}}\text{He}\) từ phản ứng hạt nhân \({}_{\text{1}}^{\text{1}}\text{H+}{}_{\text{3}}^{\text{7}}\text{Li}\to {}_{\text{2}}^{\text{4}}\text{He}\,\text{+X}\). Mỗi phản ứng trên tỏa năng lượng 17,3 MeV. Số A- vô-ga-đrô NA= 6,02.1023 mol-1. Năng lượng tỏa ra khi tổng hợp được 0,5 mol heli là
Năng lượng tỏa ra khi tổng hợp được 0,5 mol heli là 5,2.1024 MeV.
Một khung dây dẫn phẳng quay đều với tốc độ góc ω quanh một trục cố định nằm trong mặt phẳng khung dây, trong một từ trường đều có véc tơ cảm ứng từ vuông góc với trục quay của khung. Suất điện động cảm ứng trong khung có biểu thức \(e={{E}_{0}}cos\left( \omega t+\pi /3 \right)\). Tại thời điểm t = 0, vectơ pháp tuyến của mặt phẳng khung dây hợp với véc tơ cảm ứng từ một góc bằng
Véc tơ cảm ứng từ một góc bằng 1500.
Trong thí nghiệm giao thoa sóng trên mặt nước, hai nguồn AB cách nhau 14,5cm dao động ngược pha. Điểm M trên AB gần trung điểm của AB nhất, cách O một đoạn 0,5cm luôn dao động cực đại. Số điểm dao động cực đại thuộc đường elíp trên mặt nước nhận A, B làm tiêu điểm là:
Hai nguồn dao động ngược pha, ta có:
\(-\frac{1}{2}-\frac{AB}{\lambda }\le k\le \frac{AB}{\lambda }-\frac{1}{2}\)=>\(-7,75\le k\le 6,75\)
Trên AB có 14 điểm dao động với biên độ cực đại, có nghĩa là trên elíp nhận AB làm tiêu điểm có 2.14 =28 điểm dao động với biên độ cực đại.
Năng lượng để giải phóng một electron liên kết thành electron dẫn trong chất bán dẫn Ge là 0,66 eV. Giới hạn quang dẫn (hay giới hạn quang điện trong) của Ge thuộc vùng ánh sáng
Giới hạn quang dẫn (hay giới hạn quang điện trong) của Ge thuộc vùng ánh sáng hồng ngoại.
Trong thí nghiệm Y-âng về giao thoa ánh sáng, điểm M trong vùng giao thoa trên màn có hiệu khoảng cách đến hai khe là d1 – d2 = 2 μm. Ánh sáng làm thí nghiệm có bước sóng λ = 400 nm. Tại M có
Ánh sáng làm thí nghiệm có bước sóng λ = 400 nm.
Tại M có vân sáng bậc 5.
Một học sinh dùng cân và đồng hồ đếm giây để đo động cứng của lò xo. Dùng cân để cân vật nặng khối lượng m = 100g \(\pm \) 2%. Gắn vật vào lò xo và kích thích cho con lắc dao động rồi dùng đồng hồ đếm giây đo thời gian của một dao động và cho kết quả T = 2s \(\pm \) 1%. Bỏ qua sai số của π . Sai số tương đối của phép đo là:
Ta có:
\(\overline{k}=\frac{4{{\pi }^{2}}m}{{{\overline{T}}^{2}}}=1N/m\);
\(\frac{\Delta k}{\overline{k}}=\frac{2\Delta T}{\overline{T}}+\frac{\Delta m}{\overline{m}}\)
=>\(\frac{\Delta k}{1}=\frac{2.0,01}{2}+\frac{0,02}{100}\)
Cho phương trình phản ứng hạt nhân \(\alpha +{}_{7}^{14}N+1,2MeV\to X+p\). Phản ứng này
Phản ứng này thu năng lượng là 1,2 MeV.
Hạt nhân \({}_{14}^{29}Si\) có
Hạt nhân \({}_{14}^{29}Si\) có 14 prôtôn và 15 nơtron.
Khi đi xe ôtô vào ban đêm, dưới ánh đèn xe ta thấy rõ các công nhân dọn vệ sinh bên đường là nhờ họ khoác trên người một loại áo đặc biệt. Loại áo này ứng dụng hiện tượng vật lý nào sau đây?
Loại áo này ứng dụng hiện tượng vật lý là quang phát quang.
Một hạt nhân X phóng ra tia phóng xạ và biến thành hạt nhân Y bền. Biết chu kì bán rã của chất X là T. Khảo sát một mẫu chất thấy: Ở thời điểm t =0, mẫu chất là một lượng X nguyên chất; Ở thời điểm t, tỉ số khối lượng của Y và X trong mẫu là k; Ở thời điểm 2t, tỉ số khối lượng của Y và X trong mẫu là 8k. Ở thời điểm 3t, tỉ số số hạt của Y và X trong mẫu là
Ta có:
\(\frac{{{m}_{Y}}}{{{m}_{X}}}=\frac{{{A}_{Y}}}{{{A}_{X}}}({{2}^{\frac{t}{T}}}-1)\)=k;
\(\frac{{{m}_{Y}}}{{{m}_{X}}}=\frac{{{A}_{Y}}}{{{A}_{X}}}({{2}^{\frac{2t}{T}}}-1)=8k\)=>\(\frac{t}{T}=2,81\)
Vậy thời điểm 3t tỷ số:
\(\frac{{{m}_{Y}}}{{{m}_{X}}}=\frac{{{A}_{Y}}}{{{A}_{X}}}({{2}^{3.2,81}}-1)=\frac{{{N}_{Y}}}{{{N}_{X}}}\)=343,89
Nguyên tử hiđrô ở trạng thái dừng có mức năng lượng thứ n tuân theo công thức \({{\text{E}}_{\text{n}}}\text{=}\frac{\text{-13}\text{,6}}{{{\text{n}}^{\text{2}}}}\text{eV}\), với n = 1,2,3,... Khi nguyên tử hiđrô đang ở trạng thái kích thích thứ nhất thì nhận được kích thích làm bán kính quỹ đạo electron tăng lên 9 lần. Tỉ số giữa bước sóng hồng ngoại lớn nhất và bước sóng ánh sáng nhìn thấy nhỏ nhất mà nguyên tử này có thể phát ra gần nhất với giá trị nào sau đây?
Bước sóng nhìn thấy nhỏ nhất nên năng lượng lớn nhất, và phải nằm trong dãy Ban-me
⇒ chuyển từ E6 về E2.
Năng lượng của photon:
\({{\varepsilon }_{1}}=\frac{-13,6}{{{6}^{2}}}-\frac{-13,6}{{{2}^{2}}}=3,02\)
Bước sóng hồng ngoại lớn nhất nên năng lượng bé nhất ⇒ chuyển từ E6 về E5
\({{\varepsilon }_{2}}=\frac{-13,6}{{{6}^{2}}}-\frac{-13,6}{{{5}^{2}}}=0,166\);
Tỉ số: \(\frac{{{\lambda }_{2}}}{{{\lambda }_{1}}}=\frac{{{\varepsilon }_{1}}}{{{\varepsilon }_{2}}}=18,19\)
Dùng hạt prôtôn có động năng Kp = 5,58 MeV bắn vào hạt nhân \({}_{11}^{23}Na\) đứng yên thì thu được hạt α và hạt nhân X có động năng tương ứng là Kα = 6,6 MeV và KX = 2,64 MeV. Coi rằng phản ứng không kèm theo bức xạ gamma, lấy khối lượng hạt nhân tính theo đơn vị u xấp xỉ bằng số khối của nó. Góc giữa vectơ vận tốc của hạt α và hạt nhân X gần bằng giá trị nào sau đây?
Ta có:
\(\overrightarrow{{{p}_{p}}}=\overrightarrow{{{p}_{\alpha }}}+\overrightarrow{{{p}_{X}}}\Rightarrow p_{p}^{2}=p_{\alpha }^{2}+p_{X}^{2}+2p_{p}^{{}}p_{p}^{{}}\cos \varphi \Rightarrow \cos \varphi =\frac{p_{p}^{2}-p_{\alpha }^{2}-p_{X}^{2}}{2{{p}_{p}}{{p}_{X}}}\)
\(\cos \varphi =\frac{{{m}_{p}}{{K}_{p}}-{{m}_{\alpha }}{{K}_{\alpha }}-{{m}_{X}}{{K}_{X}}P_{p}^{2}-p_{\alpha }^{2}-p_{X}^{2}}{2\sqrt{{{m}_{\alpha }}{{K}_{\alpha }}{{m}_{X}}{{K}_{X}}}}=>\varphi ={{170}^{0}}\)
Trong thí nghiệm Y-âng, nguồn sáng phát đồng thời hai bức xạ đơn sắc, trong đó bức xạ màu đỏ có bước sóng λ1 = 720 nm và bức xạ màu lục có bước sóng λ2 = 560 nm. Hoit quan sát viên nhìn thấy trên màn giữa hai vân tối của hệ gần nhau nhất có bao nhiêu vân sáng màu lục?
+ Vị trí trùng nhau hai bức xạ tối:
\(\frac{2{{k}_{1}}+1}{2{{k}_{2}}+1}=\frac{{{\lambda }_{2}}}{{{\lambda }_{1}}}=\frac{7}{9}=\frac{7\left( 2n+1 \right)}{9\left( 2n+1 \right)}\to \left\{ \begin{align} & 2{{k}_{1}}+1=7\left( 2n+1 \right) \\ & 2{{k}_{2}}+1=9\left( 2n+1 \right) \\ \end{align} \right.\) ; với \(n\in \mathbb{Z}\)
+ Chọn n = 0 và n = 1 là hai vị trí gần nhau nhất vân tối hai bức xạ trên trùng nhau
\(\to \left\{ \begin{align} & {{k}_{1}}={{3,}_{{}}}{{k}_{2}}=10 \\ & {{{{k}'}}_{1}}={{4,}_{{}}}{{{{k}'}}_{2}}=13 \\ \end{align} \right.\) (cùng phía)
+ Tuy nhiên trong miền này một số vân sáng hai bức xạ trên trùng nhau. Tương tự cho bài toán vân sáng trung nhau, ta có:
\(\frac{{{k}_{1}}}{{{k}_{2}}}=\frac{{{\lambda }_{2}}}{{{\lambda }_{1}}}=\frac{7}{9}=\frac{7t}{9t}\to \left\{ \begin{align} & {{k}_{1}}=7t \\ & {{k}_{2}}=9t \\ \end{align} \right. (*)\); với \(t\in \mathbb{Z}\)
+ Vậy, trong miền hai vân tối hệ trùng nhau tính từ vân tối thứ 5 (bức xạ λ2) đến vân tối thứ 14 của bức xạ λ2 có 9 vân sáng của bức xạ λ2. Tuy nhiên có 1 vị trí vân sáng của bức xạ λ2 trung với vân sáng của λ1 nên không tính vị trí này.
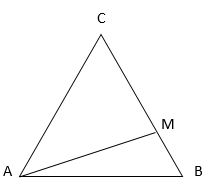
Giao thoa sóng với hai nguồn kết hợp cùng pha đặt tại AB cách nhau 50 cm với bước sóng bằng 7,5 cm. Điểm C nằm trên đường trung trực AB sao cho AC=AB. Gọi M là điểm trên đường thẳng BC và nằm trên sóng có biên độ cực đại. Khoảng cách ngắn nhất từ M đến B là.
Bước sóng: \(\lambda =4.0,5=2cm\)
Để M gần B nhất thì M phải nằm trên đường cực đại ứng với kmax = (AB/l) = 6
=> MA – MB = 6l = 45 cm (1)
Do AC = AB mà C thuộc trung trực của AB => tam giác ABC đều => B = 600
Xét DABC :
MB2 – MA2 – AB.MB + AB2 = 0 (2)
Từ (1) và (2) => MB2 – (MB+45)2 – 50.MB + 2502 = 0 (2) => 140MB =502 – 452 => MB = 3,39 (cm)
Cho mạch điện xoay chiều gồm điện trở thuần R, cuộn thuần cảm L và tụ điện C mắc nối tiếp. Đặt vào hai đầu đoạn mạch một điện áp xoay chiều \(u={{U}_{0}}cos\omega t\left( V \right)\), ω có thể thay đổi. Đồ thị sự phụ thuộc của cường độ dòng điện hiệu dụng vào ω như hình vẽ. Trong đó \({{\omega }_{2}}-{{\omega }_{1}}=400/\pi ~\left( rad/s \right)\),\(L=3\pi /4\text{ }\left( H \right)\). Điện trở R có giá trị là:
.png)
Từ đồ thị ta thấy:
\(L{{\omega }_{1}}-\frac{1}{C{{\omega }_{1}}}=\frac{1}{C{{\omega }_{2}}}-L{{\omega }_{2}}\)
=>\({{\omega }_{1}}{{\omega }_{2}}=\frac{1}{LC}=\omega _{o}^{2}\)(1)
\(\frac{U_{o}^{2}}{{{R}^{2}}}=5\frac{U_{o}^{2}}{{{R}^{2}}+{{({{\omega }_{1}}L-\frac{1}{{{\omega }_{1}}C})}^{2}}}\)
=>\(\left( {{\omega }_{1}}L-\frac{1}{{{\omega }_{1}}C} \right)=2R\)
=>\(\left( {{\omega }_{1}}L-\frac{\omega _{o}^{2}L}{{{\omega }_{1}}} \right)=2R\)(2)
Từ (1) và (2) ta có R=150Ω
Đặt điện áp \(u={{U}_{0}}cos100\pi t\text{ }\left( V \right)\) (t tính bằng s) vào đoạn mạch gồm cuộn dây và tụ điện mắc nối tiếp. Cuộn dây có độ tự cảm \(L=\frac{1,5}{\pi }(H)\), điện trở \(r=50\sqrt{3}\,\Omega \), tụ điện có điện dung \(C=\frac{{{10}^{-4}}}{\pi }(F)\). Tại thời điểm t1, điện áp tức thời giữa hai đầu cuộn dây có giá trị 150V, đến thời điểm t1 + \(\frac{1}{75}\) (s) thì điện áp giữa hai đầu tụ điện cũng bằng 150V. Giá trị U0 bằng
Ta có:
\(\begin{array}{l} \left\{ {\begin{array}{*{20}{c}} {{Z_L} = 150}\\ {{Z_C} = 100} \end{array}\left\{ {\begin{array}{*{20}{c}} {\tan \varphi = 1/\sqrt 3 \Rightarrow \varphi = \pi /6}\\ {Z = \sqrt {{R^2} + Z_{LC}^2} = 100\left( \Omega \right)} \end{array}} \right.} \right. \Rightarrow \left\{ {\begin{array}{*{20}{c}} {{Z_{RL}} = 100\sqrt 3 \left( \Omega \right)}\\ {{\varphi _{RL}} = \pi /3{\rm{ }}} \end{array}} \right..\\ i = {I_0}\cos \left( {100\pi t - \frac{\pi }{6}} \right)\\ \Rightarrow \left\{ {\begin{array}{*{20}{c}} {{u_{RL}} = {U_{0RL}}\cos \left( {100\pi t - \frac{\pi }{6} + \frac{\pi }{3}} \right)}\\ {{u_C} = {U_{0C}} = \cos \left( {100\pi t - \frac{\pi }{6} - \frac{\pi }{2}} \right)} \end{array}} \right.\\ \left\{ {\begin{array}{*{20}{c}} {{u_{RL\left( {{t_1}} \right)}} = 100\sqrt 3 {I_0}\cos \left( {100\pi {t_1} + \frac{\pi }{6}} \right) = 150V}\\ {{u_C}\left( {{t_2}} \right) = 100{I_0}\cos \left( {100\pi {t_1} + \frac{{2\pi }}{3}} \right) = 150V} \end{array}} \right.\\ \Rightarrow {\left( {\frac{{150}}{{100\sqrt 3 {I_0}}}} \right)^2} + {\left( {\frac{{150}}{{100{I_0}}}} \right)^2} = 1 = > {I_0} = \sqrt 3 \;A \end{array}\)
Từ đó suy ra:
\(=>{{U}_{0}}=Z{{I}_{0}}=100.\sqrt{3}=100\sqrt{3}\left( \text{V} \right)\)
Một con lắc lò xo đặt trên mặt phẳng nằm ngang gồm lò xo nhẹ có một đầu cố định, đầu kia gắn với vật nhỏ m1. Ban đầu giữ vật m1 tại vị trí mà lò xo bị nén 8cm, đặt vật nhỏ m2 (có khối lượng bằng khối lượng vật m1) trên mặt phẳng nằm ngang và sát với vật m1. Buông nhẹ để hai vật bắt đầu chuyển động theo phương của trục lò xo. Bỏ qua mọi ma sát. Ở thời điểm lò xo có chiều dài cực đại lần đầu tiên thì khoảng cách giữa hai vật m1 và m2 là
Vật \({{m}_{2}}\) sẽ tác dụng ra khỏi vật \({{m}_{1}}\) tại vị trí cân bằng của hệ, bỏi vì tại vị trí này:
+) Vật \({{m}_{1}}\) có tốc độ cực đại và bắt đầu giảm
+) Vật \({{m}_{2}}\)sẽ tiếp tục chuyển động thẳng đều với tốc độ bằng tốc độ cực đại
Lò xo có độ dài cực đại là đầu tiên ứng với khoảng thời gian:
\(\frac{T}{4}\), khi đó Khoảng cách giữa hai vật là \(\Delta x=\omega A\frac{T}{4}-A=4,6cm\)
Điện năng được truyền từ đường dây điện một pha có điện áp hiệu dụng ổn định 220V vào nhà một hộ dân bằng đường dây tải điện có chất lượng kém. Trong nhà của hộ dân này, dùng một máy biến áp lí tưởng để duy trì điện áp hiêu dụng ở đầu ra luôn là 220V (gọi là ổn áp). Máy ổn áp này chỉ hoạt động khi điện áp hiệu dụng ở đầu vào lớn hơn 110V. Tính toán cho thấy, nếu công suất sử dụng điện trong là 1,1 kW thì tỉ số giữa điện áp hiệu dụng ở đầu ra và điện áp hiệu dụng ở đầu vào (tỉ số tăng áp) của máy ổn áp là 1,1. Coi điện áp và cường độ dòng điện luôn cùng pha. Nếu công suất sử dụng điện trong nhà là 2,2 kW thì tỉ số tăng áp của máy ổn áp bằng.
Theo đề bài: điện áp đầu ra của MBA luôn là 220V => U21 = U22 = 220V
+ TH1: Khi công suất tiêu thụ điện của hộ gia đình là 1,1kW => P1 = U21.I21 Þ I21 = 5A
Hệ số tăng áp của MBA là 1,1 => I11 = 1,1I21 = 5,5
Độ giảm thế trên đường dây truyền tải: DU1 = U0 – U11 = 20V = I11.R => R = 40/11 W
+ TH2: Khi công suất tiêu thụ điện của hộ gia đình là 2,2kW => P2 = U22.I22 Þ I22 = 10A
Hệ số tăng áp của MBA là k
=> I21 = kI22 = 10k (A)
Độ giảm thế trên đường dây truyền tải: DU2 = U0 – U12 = I21.R
Theo đề bài MBA chỉ hoạt động khi U1 > 110V => k < 2 => k =1,26
Hai chất điểm dao động điều hòa cùng tần số trên hai đường thẳng song song, cách nhau 5cm và song song với trục tọa độ Ox.Đồ thị biểu diễn sự phụ thuộc li độ của 2 vật theo thời gian như như hình vẽ. Vị trí cân bằng của hai chất điểm cùng ở trên một đường thẳng qua gốc tọa độ và vuông góc với Ox. Biết \({{t}_{2}}-{{t}_{1}}=1,08\text{s}\). Kể từ lúc \(t=0\), hai chất điểm cách nhau \(5\sqrt{3}\)cm lần thứ 2017 ở thời điểm gần nhất thời điểm nào sau đây?
.png)
.png)
Phương trình dao động của hai chất điểm:
\(\left\{ \begin{align} & {{x}_{1}}=5\sqrt{3}\cos \left( \omega t+\frac{\pi }{2} \right) \\ & {{x}_{2}}=5\cos \left( \omega t \right) \\ \end{align} \right.\)
\(\Leftrightarrow \left\{ \begin{align} & {{x}_{1}}=-5\sqrt{3}\sin \left( \omega t \right) \\ & {{x}_{2}}=5\cos \left( \omega t \right) \\ \end{align} \right.\)
Khi hai chất điểm có cùng li độ
\({{x}_{1}}={{x}_{2}}\Leftrightarrow -5\sqrt{3}\sin \left( \omega t \right)=5\cos \left( \omega t \right)\Leftrightarrow \tan \left( \omega t \right)=-\frac{1}{\sqrt{3}}\Leftrightarrow \omega t=-\frac{\pi }{6}+k\pi \)
Hai chất điểm gặp nhau lần thứ nhất t1 và lần thứ 4 t2 ứng với hai giá trị của \(k=1,4\)
Ta có:
\({{t}_{2}}-{{t}_{1}}=\frac{3\pi }{\omega }\Leftrightarrow 1,08=\frac{3\pi }{\omega }\Rightarrow \omega =\frac{25}{9}\pi \)rad/s
+ Khoảng cách giữa hai chất điểm
\(d=\sqrt{{{5}^{2}}+{{\left( {{x}_{1}}-{{x}_{2}} \right)}^{2}}}=\sqrt{5+\Delta {{x}^{2}}}\)
Với \(\Delta x=10\cos \left( \omega t+\frac{2\pi }{3} \right)\)cm
Tại vị trí khoảng cách giữa hai chất điểm là \(5\sqrt{3}\)cm thì \(\Delta x=\pm 5\sqrt{2}\)cm
+ Mỗi chu kì \(\Delta x=\pm 5\sqrt{2}\)cm bốn lần, vậy ta cần 504T để thõa mãn điều kiện trên 2016 lần. Vây
\(t=504T+{{t}_{\varphi }}=504.0,72+\frac{105}{360}0,72=363,09\text{s}\)