Từ phương trình ta có: \(\frac{2\pi x}{\lambda }=\pi x\Rightarrow \lambda =2m\)

Tốc độ truyền sóng: \(v=\lambda .f=\lambda .\frac{\omega }{2\pi }=2.\frac{20\pi }{2\pi }=20\text{m/s}\)

Chu kì dao động của con lắc lò xo: \(T=2\pi \sqrt{\frac{m}{k}}\)

Ta có: \(\lambda =vT=v\frac{2\pi }{\omega }\)

A, B, C – đúng; D – sai.

Ta có từ thông \(\Phi =NBS\cos \alpha \)

Từ thông sẽ không thay đổi nếu khung dây chuyển động tịnh tiến theo một phương bất kì. 

Khi cộng hưởng xảy ra \(\omega ={{\omega }_{0}}\)hay \(f={{f}_{0}}\)

Vận tốc của vật dao động điều hòa có độ lớn cực đại: \({{v}_{\max }}=A\omega \)

Ta có, mức cường độ âm: \(L=10\log \frac{I}{{{I}_{0}}}=10\log \frac{{{10}^{-4}}}{{{10}^{-12}}}=80dB\)

Biên độ dao động của chất điểm: \(A=2\sqrt{2}cm\)

Ta có: \(\frac{{{U}_{1}}}{{{U}_{2}}}=\frac{{{N}_{1}}}{{{N}_{2}}}\)

Lại có máy hạ áp \({{U}_{2}}<{{U}_{1}}\Rightarrow {{N}_{2}}<{{N}_{1}}\)

Suất điện động sinh ra tại 3 cuộn dây:

\(\left\{ {\begin{array}{*{20}{l}}
{{e_1} = {E_0}\cos (\omega t)}\\
{{e_1} = {E_0}\cos \left( {\omega t + \frac{{2\pi }}{3}} \right)}\\
{{e_2} = {E_0}\cos \left( {\omega t - \frac{{2\pi }}{3}} \right)}
\end{array}} \right.\)

\(\Rightarrow {{e}_{1}}+{{e}_{2}}={{E}_{0}}\cos (\omega t)+{{E}_{0}}\cos \left( \omega t+\frac{2\pi }{3} \right)=2{{E}_{0}}\cos \frac{\pi }{3}.\cos \left( \omega t+\frac{\pi }{3} \right)\)

\(={{E}_{0}}\cos \left( \omega t+\frac{\pi }{3} \right)=-{{E}_{0}}\cos \left( \omega t-\frac{2\pi }{3} \right)=-{{e}_{3}}\)

Ta có:

\(\left\{ {\begin{array}{*{20}{l}}
{{u_{(t)}} = {U_0}\cos \left( {100\pi t + \frac{\pi }{3}} \right)}\\
{{i_{(t)}} = {I_0}\cos \left( {100\pi t + \frac{\pi }{3} - \frac{\pi }{2}} \right) = {I_0}\cos \left( {100\pi t - \frac{\pi }{6}} \right)}
\end{array}} \right.\)

\(\Rightarrow {{i}_{\left( t+\frac{T}{4} \right)}}={{I}_{0}}\cos \left( 100\pi \left( t+\frac{T}{4} \right)-\frac{\pi }{6} \right)={{I}_{0}}\cos \left( 100\pi t+\frac{\pi }{3} \right)\)

\(\Rightarrow \frac{{{u}_{(t)}}}{i\left( t+\frac{T}{4} \right)}=\frac{{{U}_{0}}}{{{I}_{0}}}={{Z}_{L}}=\omega L=100\pi \frac{1}{2\pi }=50\Omega \)

Ta có chu kì dao động con lắc đơn: \(T=2\pi \sqrt{\frac{l}{g}}\)

Khi chiều dài con lắc đơn tăng 20% tức là \({l}'=l+0,2l=1,2l\) thì chu kì dao động của con lắc khi đó

\({T}'=\sqrt{1,2}T\) hay chu kì dao động tăng 9,545%

Tốc độ truyền sóng là tốc độ lan truyền dao động trong môi trường truyền sóng.

Đại lượng giúp ta phân biệt âm do các nguồn âm khác nhau phát ra là âm sắc. 

Mạch chỉ có điện trở, công suất tiêu thụ: \(P=UI\cos \varphi =\frac{{{U}^{2}}}{R}\) không phụ thuộc vào tần số 

\(\Rightarrow {{P}_{1}}={{P}_{2}}\)

Ta có in nhanh pha hơn u 

\(\Rightarrow \) X là tụ điện có dung kháng \({{Z}_{C}}=\frac{{{U}_{0}}}{{{I}_{0}}}=\frac{100\sqrt{2}}{\sqrt{2}}=100\Omega =\frac{1}{\omega C}\Rightarrow C=\frac{{{10}^{-4}}}{\pi }F\)

Cảm kháng: \({{Z}_{L}}=\omega L\)

A – đúng, B, C, D - sai

Để 2 sóng có thể giao thoa được với nhau thì chúng xuất phát từ 2 nguồn kết hợp là 2 nguồn có cùng phương, cùng tần số và có độ lệch pha không đổi theo thời gian.

Tổng trở của mạch dao động: \(Z=\sqrt{{{R}^{2}}+{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}}\)

Q đặt tại trung điểm của MN và đứng yên

Q - có thể là điện tích bất kì (có thể âm hoặc dương)

Năng lượng của vật dao động điều hòa: \(W=\frac{1}{2}k{{A}^{2}}=\frac{1}{2}m{{\omega }^{2}}{{A}^{2}}\)

A – đúng

B – sai vì tỉ lệ với bình phương biên độ.

C – sai vì động năng tại vị trí có li độ cực đại bằng 0J.

D – sai vì thế năng tại VTCB bằng 0J.  

Biên độ dao động cưỡng bức không phụ thuộc vào pha ban đầu của ngoại lực tuần hoàn tác dụng lên vật.

Từ phương trình, ta có độ lệch pha của u so với i: \(\varphi =\frac{\pi }{2}-\frac{\pi }{6}=\frac{\pi }{3}\)

Tổng trở của mạch: \(Z=\frac{{{U}_{0}}}{{{I}_{0}}}=110\Omega \)

Lại có: \(\cos \varphi =\frac{R}{Z}\Rightarrow R=Z.\cos \varphi =110.\cos \frac{\pi }{3}=55\Omega \)

+ Biên độ dao động: \(A=\frac{32-20}{2}=6cm=0,06m\)

+ Cơ năng của vật: \(W=\frac{1}{2}k{{A}^{2}}=\frac{1}{2}{{100.0,06}^{2}}=0,18J\)

Dung kháng: \({{Z}_{C}}=\frac{1}{\omega C}=100\Omega \)

Điện trở: \(R=50\sqrt{3}\Omega \)

Lại có: \({{\varphi }_{AM}}-{{\varphi }_{AB}}=\frac{\pi }{3}\)

\(\tan \left( {{\varphi }_{AM}}-{{\varphi }_{AB}} \right)=\frac{\tan {{\varphi }_{AM}}-\tan {{\varphi }_{AB}}}{1+\tan {{\varphi }_{AM}}\tan {{\varphi }_{AB}}}\)

\(\Leftrightarrow \tan \frac{\pi }{3}=\frac{\frac{{{Z}_{L}}}{R}-\frac{{{Z}_{L}}-{{Z}_{C}}}{R}}{1+\frac{{{Z}_{L}}}{R}\frac{{{Z}_{L}}-{{Z}_{C}}}{R}}\Leftrightarrow \sqrt{3}=\frac{\frac{{{Z}_{L}}}{50\sqrt{3}}-\frac{{{Z}_{L}}-100}{50\sqrt{3}}}{1+\frac{{{Z}_{L}}}{50\sqrt{3}}\frac{{{Z}_{L}}-100}{50\sqrt{3}}}\)

\(\Rightarrow {{Z}_{L}}=50\Omega \Rightarrow L=\frac{{{Z}_{L}}}{\omega }=\frac{1}{2\pi }H\)

Hiệu điện thế giữa 2 cực cảu nguồn điện: \(U=I.R\Leftrightarrow 12=I.4,8\Rightarrow I=2,5A\)

Lại có: \(I=\frac{E}{R+r}\Rightarrow E=I(R+r)=2,5(4,8+0,1)=12,25V\)

Ta có: \(l=90cm=0,9m\)

Trên dây có 10 nút, 9 bụng

Sử dụng điều kiện có sóng dừng trên dây hai đầu cố định: \(l=k\frac{\lambda }{2}\Leftrightarrow 90=9\frac{\lambda }{2}\Rightarrow \lambda =20cm\)

Khoảng cách giữa M và N: \(MN=57-22=35cm\)

Độ lệch pha giữa 2 điểm M và N: \(\Delta \varphi =\frac{2\pi MN}{\lambda }=\frac{2\pi .35}{20}=\frac{7\pi }{2}\)

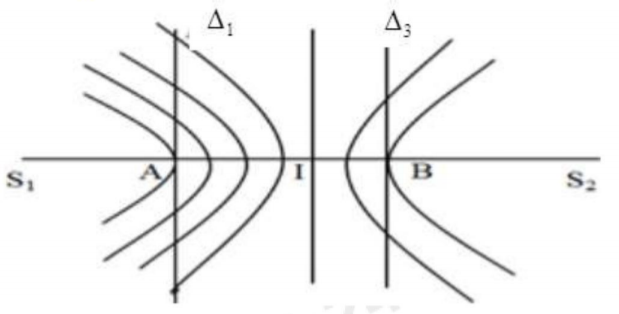
+ Trường hợp \({{\Delta }_{1}}\) và \({{\Delta }_{3}}\)khác phía so với vận trung tâm: 

Từ hình vẽ thấy, để trên \({{\Delta }_{1}}\) có 7 cực đại, tại điểm A là cực đại bậc 4 \(\Rightarrow IA=4\frac{\lambda }{2}=2\lambda \)

Trên \({{\Delta }_{3}}\)có 3 cực đại, tại điểm B là cực đại bậc \(-2:IB=2\frac{\lambda }{2}=\lambda \)

Khoảng cách giữa \({{\Delta }_{1}}\) và \({{\Delta }_{3}}\)là: \(3\lambda \)

Gọi C là điểm mà \({{\Delta }_{2}}\)cắt AB và \({{\Delta }_{2}}\)cách đều \({{\Delta }_{1}},{{\Delta }_{3}}\Rightarrow C\)là cực đại bậc 1 

\(\Rightarrow \) Trên \({{\Delta }_{2}}\)có 1 cực đại

Trường hợp \({{\Delta }_{1}}\) và \({{\Delta }_{3}}\)cùng phía so với vận trung tâm:

Từ hình vẽ thấy, để trên \({{\Delta }_{1}}\) có 7 cực đại, tại điểm A là cực đại bậc 4 \(\Rightarrow IA=4\frac{\lambda }{2}=2\lambda \)

Trên \({{\Delta }_{3}}\)có 3 cực đại, tại điểm B là cực đại bậc 2: \(IB=2\frac{\lambda }{2}=\lambda \)

Gọi C là điểm mà \({{\Delta }_{2}}\)cắt AB và \({{\Delta }_{2}}\)cách đều \({{\Delta }_{1}},{{\Delta }_{3}}\Rightarrow C\) là cực đại bậc 3.

\(\Rightarrow \) Trên \({{\Delta }_{2}}\)có \(2.2+1=5\)cực đại

Ta có: \(T=2\pi \sqrt{\frac{l}{g}}\Rightarrow g=\frac{4{{\pi }^{2}}l}{{{T}^{2}}}\)

Chu kì dao động đo được: \(T=\frac{t}{10}=2,0102\pm 0,0269s\)

\(\Rightarrow \bar{g}=\frac{4{{\pi }^{2}}\bar{l}}{{{{\bar{T}}}^{2}}}=\frac{4{{\pi }^{2}}.1}{{{2,0102}^{2}}}=9,899\text{m/}{{\text{s}}^{\text{2}}}\)

Sai số: \(\overline{\Delta g}=\left( \frac{\Delta l}{\overline{l}}+2\frac{\Delta T}{\overline{T}} \right)\overline{g}\)

\(\Rightarrow \overline{\Delta g}=\left( \frac{0,001}{1}+2\frac{0,0269}{2,0102} \right)\cdot 9,899=0,275\text{m/}{{\text{s}}^{\text{2}}}\)

Ta có: \(\frac{{{u}_{L}}}{{{u}_{C}}}=-\frac{{{Z}_{L}}}{{{Z}_{C}}}=-3\Rightarrow {{u}_{C}}=-\frac{{{u}_{L}}}{3}\)

Lại có: \(u={{u}_{R}}+{{u}_{L}}+{{u}_{C}}\Leftrightarrow 200=120+{{u}_{L}}-\frac{{{u}_{L}}}{3}\Rightarrow {{u}_{L}}=120V\)

Ta có: \(x={{x}_{1}}+{{x}_{2}}=3\angle -\frac{\pi }{6}+3\angle \frac{\pi }{2}=3\angle \frac{\pi }{6}\Rightarrow x=3\cos \left( \omega t+\frac{\pi }{6} \right)cm\)

Ta có: 

\(\left\{ {\begin{array}{*{20}{l}}
{R = 30\Omega }\\
{{Z_L} = \omega L = 100\Omega }\\
{{Z_C} = \frac{1}{{\omega C}} = 70\Omega }
\end{array}} \right.\)

Lại có: \(\bar{i}=\frac{{\bar{u}}}{{\bar{Z}}}=\frac{120\sqrt{2}\angle 0}{30+(100-70)i}=4\angle -\frac{\pi }{4}\Rightarrow i=4\cos \left( 100\pi t-\frac{\pi }{4} \right)A\)

Ta có: \(l=(2k+1)\frac{\lambda }{4}=(2.2+1)\frac{\lambda }{4}=\frac{5.60}{4}=75cm\)

Ta có giản đồ vecto:

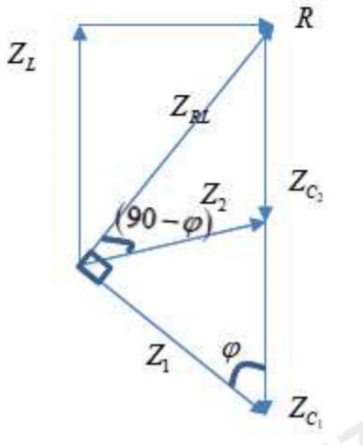
Ta có \(\frac{{{U}_{0{{C}_{1}}}}}{{{U}_{0AB}}}=\frac{100}{50}=\frac{{{Z}_{{{C}_{1}}}}}{{{Z}_{1}}}=\frac{1}{\cos \varphi }\)

\(\Rightarrow \cos \varphi =\frac{1}{2}\Rightarrow \varphi ={{60}^{0}}\)

Lại có: \(\frac{{{U}_{0}}}{{{U}_{0AB}}}=\frac{{{U}_{0}}}{50}=\frac{{{Z}_{RL}}}{{{Z}_{2}}}=\sqrt{3}\Rightarrow {{U}_{0}}=50\sqrt{3}V\)

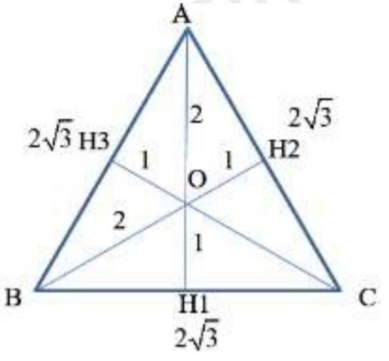
Ta có: Bước sóng \(\lambda =1cm\)

Các điểm dao động cùng pha với O khi cách O một số nguyên lần bước sóng. 

Ta có: \(OA=OB=OC=2cm=2\lambda \)

\(O{{H}_{1}}=O{{H}_{2}}=O{{H}_{3}}=1cm=\lambda \)

\(\Rightarrow \) Trên mỗi cạnh của tam giác có số phần tử nước dao động cùng pha với nguồn là 3 điểm (2 đỉnh của tam giác và trung điểm của cạnh đó)

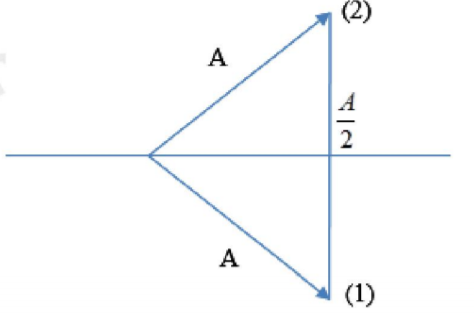
+ Chu kì dao động của (1): \({{T}_{1}}=\frac{2\pi }{{{\omega }_{1}}}=\frac{2}{3}s\)

+ Chu kì dao động của (2): \({{T}_{2}}=\frac{2\pi }{{{\omega }_{2}}}=\frac{1}{2}s\)

Để trạng thái của 2 vật lặp lại như ban đầu thì thời gian phải là bội chung của \(\left( {{T}_{1}},{{T}_{2}} \right)\)

Ta có: \(BCNN\left( {{T}_{1}},{{T}_{2}} \right)=BCNN\left( \frac{2}{3},\frac{1}{2} \right)\)

Từ các đáp án ta có 2, 3 là bội chung của \(\left( {{T}_{1}},{{T}_{2}} \right)\)

\(\Rightarrow \) Thời gian ngắn nhất là 2s

Mạch có RL

Khi roto của máy quay đều với tốc độ n vòng/phút: \(U=1\sqrt{{{R}^{2}}+Z_{L}^{2}}\text{      (1)}\)

Khi roto của máy quay đều với tốc độ 3n vòng/phút : \(3U=\sqrt{3}\sqrt{{{R}^{2}}+9Z_{L}^{2}}\text{     (2)}\)

Từ (1) và (2) suy ra: \(\frac{\sqrt{3}\sqrt{{{R}^{2}}+9Z_{L}^{2}}}{\sqrt{{{R}^{2}}+Z_{L}^{2}}}=\frac{3U}{U}\Rightarrow {{Z}_{L}}=\frac{R}{\sqrt{3}}\)

Nếu roto của máy quay đều với tốc độ 20 vòng/phút thì: \(2U=I\sqrt{{{R}^{2}}+4Z_{L}^{2}}\text{     (3)}\)

Lấy \(\frac{(1)}{(3)}\)  ta được: \(\frac{U}{2U}=\frac{1\sqrt{3Z_{L}^{2}+Z_{L}^{2}}}{I\sqrt{3Z_{L}^{2}+4Z_{L}^{2}}}\Rightarrow I=\frac{4}{\sqrt{7}}A\)

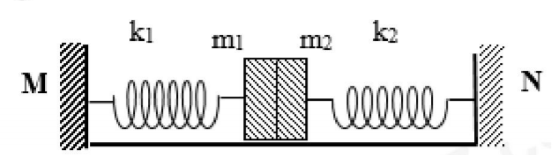
+ Biên độ dao động: A= 8cm 

+ Ban đầu: \({{v}_{1}}={{v}_{2}}=\omega A=\sqrt{\frac{k}{{{m}_{1}}+{{m}_{2}}}}\cdot A=\sqrt{\frac{k}{2m}}A\)

Thời gian vật đi từ VTCB đến biên lần đầu: \(\Delta t=\frac{{{T}'}}{4}=\frac{2\pi \sqrt{\frac{m}{k}}}{4}\)

Vật (2) khi đó chuyển động thẳng đều trong khoảng thời gian \(\Delta t\)

Ta có, quãng đường vật (2) đi được: 

\(S={{v}_{2}}\Delta t=\sqrt{\frac{k}{2m}}.A.\frac{{{T}'}}{4}=\sqrt{\frac{k}{2m}}.8.\frac{2\pi }{4}\sqrt{\frac{m}{k}}=2\sqrt{2}\pi (m)\)

Khoảng cách cần tìm: \(S-{A}'=2\sqrt{2}\pi -4\sqrt{2}=3,23cm\)