Số nuclon của Th nhiều hơn của Po một lượng ΔΑ = A_Th - A_Po = 230 - 210 = 20

+ Điện áp cực đại bằng 220√2V => A sai

+ Chu kì của điện áp này bằng 0,02 s => B đúng 

+ Pha ban đầu của điện áp bằng 0 rad => C sai

+ Ở thời điểm ban đầu điện áp có giá trị u = 220√2V => D sai

Số hạt nhân bị phân rã là

\(\Delta N = {N_0}.\left( {1 - {e^{ - \frac{t}{T}}}} \right) = {N_0}.\left( {1 - {e^{ - \lambda t}}} \right)\)

Năng lượng của phô-tôn

\(\varepsilon  = hf = \frac{{hc}}{\lambda } = {3,37.10^{ - 19}}\left( J \right) = 2,1\left( {eV} \right)\)

Tia γ và tia X đều là sóng điện từ không phải hạt mang điện nên khi vào trong từ trường hay điện trường đều không bị lệch hướng đi.

Tia α và β là những dòng hạt mang điện tích nên khi vào điện trường hay từ trường thì bị lệch đường đi.

Ta có:

\({\lambda ^/} = \frac{\lambda }{n} = \frac{{600}}{{4/3}} = 450\left( {nm} \right)\)

Vận tốc cực đại là v_max = 10π cm/s => A sai đơn vị

+ Biên độ dao động: \(A = \frac{{{v_{\max }}}}{\omega } = \frac{{10\pi }}{{2\pi }} = 5\left( {cm} \right)\) => B đúng => Chọn B.

+ Chu kì dao động bằng 1 s => C sai

+ Gia tốc cực đại của chất điểm bằng 20π² cm/s² => D sai đơn vị

+ Đại lượng đặc trưng cho mức bền vững của hạt nhân là năng lượng liên kết riêng

+ Năng lượng liên kết riêng càng lớn thì càng bền vững.

Khi có sóng dừng, khoảng cách giữa hai nút hoặc giữa hai bụng liền kề bằng nửa bước sóng.

Ta có:

\(T = 2\pi \sqrt {\frac{\ell }{g}}  \Rightarrow \ell  = \frac{{{T^2}g}}{{4{\pi ^2}}} = \frac{{{1^2}.9,8}}{{4{\pi ^2}}} = 0,248\left( m \right) = 24,8\left( {cm} \right)\)

Ta có: 

\(\begin{array}{l}
\frac{{{N_1}}}{{{N_2}}} = \frac{{{U_1}}}{{{U_2}}} = \frac{{{I_2}}}{{{I_1}}}\\
{N_1} > {N_2} \Rightarrow \left\{ \begin{array}{l}
{U_2} < {U_1}\\
{I_2} > {I_1}
\end{array} \right.
\end{array}\)

=> tăng dòng điện và giảm điện áp 

Ta có:

\(\begin{array}{l}
T = 2\pi \sqrt {\frac{{m + M}}{k}} \\
 \Rightarrow M = \frac{k}{{4{\pi ^2}}}{T^2} - m = 54,42\left( {kg} \right)
\end{array}\)

Sóng tại M trễ pha hơn tại nguồn A một lượng:  

\(\begin{array}{l}
\Delta \varphi  = \frac{{2\pi x}}{\lambda }\\
 \Rightarrow {u_M} = a\cos \left( {\omega t - \frac{{2\pi x}}{\lambda }} \right)
\end{array}\)

+ Vì đèn sáng bình thường nên điện áp hai đầu đèn là U_đ = U_R = 110 V

+ Ta có: \(\cos \varphi  = \frac{R}{Z} = \frac{{{U_R}}}{U} = \frac{{110}}{{220}} \Rightarrow \varphi  = \frac{\pi }{3}\) 

Bước sóng:

\(\lambda  = \frac{v}{f} = \frac{{360}}{{600}} = 0,6\left( m \right) = 60\left( {cm} \right)\) 

 Khoảng cách giữa hai điểm gần nhau nhất dao động ngược pha là:

\({d_{\min }} = \frac{\lambda }{2} = 30\left( {cm} \right)\)

Các phần tử môi trường chỉ dao động tại chỗ không truyền đi theo sóng => C sai.

Ta có:  

\(\begin{array}{l}
Z = \frac{{{U_0}}}{{{I_0}}} = 110\Omega ;\varphi  = {\varphi _u} - {\varphi _i} = \frac{\pi }{3}\\
\cos \varphi  = \frac{R}{Z} \Rightarrow R = Z\cos \varphi  = 110\cos \left( {\frac{\pi }{3}} \right) = 55\Omega 
\end{array}\)

Ta có: 

\(\begin{array}{l}
\left\{ \begin{array}{l}
{I_1} = \frac{P}{{4\pi R_1^2}}\\
{I_2} = \frac{P}{{4\pi R_2^2}}
\end{array} \right. \Rightarrow \frac{{{I_1}}}{{{I_2}}} = \frac{{R_2^2}}{{R_1^2}} = \frac{{{{\left( {{R_1} - d} \right)}^2}}}{{R_1^2}} \Leftrightarrow {\left( {\frac{{{R_1} - d}}{{{R_1}}}} \right)^2} = \frac{1}{4}\\
 \Rightarrow \frac{{{R_1} - d}}{{{R_1}}} = \frac{1}{2} \Rightarrow {R_1} = 2d = 20m
\end{array}\)

Ta có:

\(\lambda  = \frac{c}{f} = \frac{{{{3.10}^8}}}{{{{96.10}^6}}} = 3,125\left( m \right)\)

 => thuộc dải sóng cực ngắn (có λ từ 0,01 m đến 10m) 

+ Hiệu đường đi hay hiệu quang trình được xác định bởi:

\({d_1} - {d_2} = \frac{{a.x}}{D}\) 

+ Nếu tại M là vân sáng (cực đại) thì:

\({d_1} - {d_2} = k\lambda  \Rightarrow x = k\frac{{\lambda D}}{a}\) 

+ Nếu tại M là vân tối (cực tiểu) thì:

\({d_1} - {d_2} = \left( {k + 0,5} \right)\lambda  \Rightarrow x = \left( {k + 0,5} \right)\frac{{\lambda D}}{a}\) 

Ta có: L = A.d.(n_t - n_đ) = 8π/180 .1,5.10³ (l,54 - 1,50) = 8,4(mm) 

Tia γ, tia X, tia tử ngoại, ánh sáng nhìn thấy, tia hồng ngoại đều có bản chất là sóng điện từ => C sai

Khi chuyển từ mức năng lượng cao về mức năng lương thấp hơn thì phát ra một phôtôn có năng lượng:

\(\varepsilon  = {E_n} - {E_m} = {E_{cao}} - {E_{thap}} =  - 1,5 - \left( { - 13,6} \right) = 12,1\left( V \right)\)

Tại thời điểm tụ bắt đầu phóng điện thì 

\(q = {Q_0} \Rightarrow {\varphi _q} = 0 \Rightarrow {\varphi _i} = \frac{\pi }{2}\)

Câu A, B sai vì chất khí hay hơi ở áp suất thấp được kích thích bằng nhiệt hay bằng điện cho quang phổ vạch

+ Câu Β đúng vì quang phổ vạch của nguyên tố nào thì đặc trung cho nguyên tố ấy

+ Câu C sai vì quang phổ liên tục không đặc trưng cho thành phần cấu tạo chất hay nguyên tố.

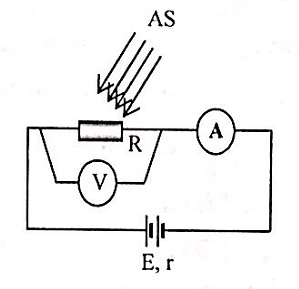
+ Số chỉ A là: I=E/(R+r). Khi tắt ánh sáng thì R tăng => I giảm => số chỉ A giảm

+ Lại có:

\(V = {U_R} = I.R = \frac{{E.R}}{{R + r}} = \frac{E}{{1 + \frac{r}{R}}}\) .

Vì R tăng nên r/R  giảm => E/ (1+r/R) tăng

=> số chỉ V tăng 

Định luật bào toàn động lượng:  

\(\begin{array}{l}
{\overrightarrow p _\alpha } = {\overrightarrow p _p} + {\overrightarrow p _n}\\
p_\alpha ^2 = p_p^2 + p_n^2 + 2{p_\alpha }{p_n}\\
 \Leftrightarrow {m_\alpha }{W_\alpha } = {m_p}{W_p} + {m_n}{W_n} + 2\sqrt {{m_p}{W_p}{m_n}{W_n}} \\
 \Leftrightarrow 4{W_\alpha } = 30{W_p} + {W_n} + 2\sqrt {30{W_p}.{W_n}} \\
\frac{{{W_p}}}{{{W_n}}} = \frac{{{m_p}}}{{{m_n}}} = 30 \Rightarrow {W_p} = 30{W_n}\\
4{W_\alpha } = {30^2}{W_n} + {W_n} + 2\sqrt {{{30}^2}{W_n}{W_n}} \\
 \Rightarrow 4{W_\alpha } = 961{W_n} \Rightarrow 4{W_\alpha } - 961{W_n} = 0
\end{array}\)

+ Phản ứng thu năng lượng nên:

\(\begin{array}{l}
{W_p} + {W_n} - {W_\alpha } =  - 2,7 \Leftrightarrow {W_\alpha } - 31{W_n} = 2,7\\
{W_\alpha } = 3,1MeV
\end{array}\)

+ Ta có: 

\(\begin{array}{l}
{W_d} + {W_t} = 3{W_d} + \frac{{{W_t}}}{3}\\
 \Rightarrow 2{W_d} = \frac{{2{W_t}}}{3} \Rightarrow {W_d} = \frac{{{W_t}}}{3} \Rightarrow {x_1} =  \pm \frac{{A\sqrt 3 }}{2}
\end{array}\)

+ Vậy thời gian ngắn nhất khi đi từ 

\({x_1} = \frac{{A\sqrt 3 }}{2} \to {x_2} = \frac{A}{2} \Rightarrow \Delta t = \frac{T}{{12}}\)

+ Mặt khác, cứ sau T/4 thì động năng lại bằng thế năng nên:

\(\frac{T}{4} = 0,3\left( s \right) \Rightarrow T = 1,2\left( s \right) \Rightarrow \Delta t = 0,1\left( s \right)\)

Hai con lắc dao động cùng pha nên:  

\(\begin{array}{l}
\left\{ \begin{array}{l}
{x_1} = 10\cos \left( {\omega t + \varphi } \right)\\
{x_2} = 5\cos \left( {\omega t + \varphi } \right)
\end{array} \right.\\
 \Rightarrow {x_1} = 2{x_2}{W_{t1}} = 4{W_{t2}}
\end{array}\) 

+ Khi thế năng con lắc thứ 2 bằng 0,005J thì thế năng con lắc thứ nhất là:

\({W_{t1}} = 4{W_{t2}} = 4.0,005 = 0,02\left( J \right)\) 

+ Vậy cơ năng của con lắc thứ nhất là:

\({W_1} = {W_{d1}} + {W_{t1}} = 0,06 + 0,02 = 0,08J\) 

+ Cơ năng của con lắc thứ nhất:  

\(\begin{array}{l}
{W_t} = \frac{1}{2}m{\omega ^2}A_1^2 = \frac{1}{2}m{\left( {\frac{{2\pi }}{T}} \right)^2}A_1^2\\
 \Rightarrow m = \frac{{2{W_1}}}{{{{\left( {\frac{{2\pi }}{T}} \right)}^2}A_1^2}} = 0,4kg
\end{array}\)

Ta có:

\(\begin{array}{l}
\varphi  = {\varphi _u} - {\varphi _i} =  - \frac{\pi }{2}\\
 \Rightarrow X \equiv C\\
 \Rightarrow {Z_C} = \frac{{{U_0}}}{{{I_0}}} = 100\Omega  \Rightarrow C = \frac{{{{10}^{ - 4}}}}{\pi }\left( F \right)
\end{array}\)

Ta có:  

 \(\begin{array}{l}
{A^2} = A_1^2 + A_2^2 + 2{A_1}{A_2}\cos \left( {\frac{\pi }{2} + \frac{\pi }{6}} \right)\\
 \Rightarrow {A^2} = A_1^2 + A_2^2 - 2{A_1}{A_2}.\frac{1}{2}\\
 \Rightarrow 3 = \underbrace {{{\left( {{A_2} - \frac{1}{2}{A_1}} \right)}^2}}_0 + \frac{3}{4}A_1^2\\
 \Rightarrow {A_1} = \max  \Leftrightarrow {\left( {{A_2} - \frac{1}{2}{A_1}} \right)^2} = 0 \Rightarrow {A_1} = 2{\rm{ cm}} \Rightarrow {A_2} = 1{\rm{ cm}}
\end{array}\)

+ Vì R1 và R2 cho cùng P = 120W nên ta có:

\(\left\{ \begin{array}{l}
{R_1} + {R_2} = \frac{{{U^2}}}{P} \Rightarrow P = \frac{{{U^2}}}{{{R_1} + {R_2}}}\\
{R_1}{R_2} = {\left( {{Z_L} - {Z_C}} \right)^2}
\end{array} \right.\) 

+ Công suất cực đại:  

\(\begin{array}{l}
{P_{\max }} = \frac{{{U^2}}}{{2\left| {{Z_L} - {Z_C}} \right|}} = \frac{{{U^2}}}{{2\sqrt {{R_1}{R_2}} }}\\
 \Rightarrow \frac{{{P_{\max }}}}{P} = \frac{{{R_1} + {R_2}}}{{2\sqrt {{R_1}{R_2}} }}\\
 \Rightarrow {P_{\max }} = \frac{P}{2}\sqrt {\frac{{{{\left( {{R_1} + {R_2}} \right)}^2}}}{{{R_1}{R_2}}}}  = \frac{P}{2}\sqrt {\frac{{{R_1}}}{{{R_2}}} + \frac{{{R_2}}}{{{R_1}}} + 2}  = \frac{{180}}{2}\sqrt {7 + 2}  = 270\left( W \right)
\end{array}\)

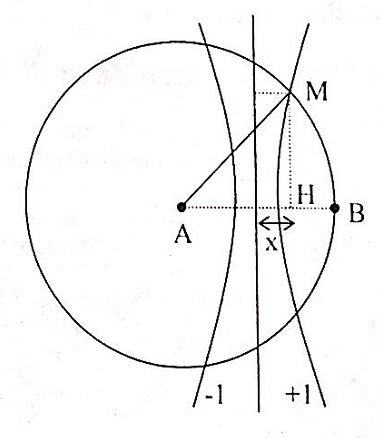
+ Vì hai nguồn cùng pha và điểm M thuộc cực đại nên: MA - MB = kλ

+ M gần trung trực nhất nên M thuộc cực đại k = ±1

+ Vì M gần A nên M thuộc k = -1 => MA - MB = -λ

+ Ta có:  

\(\begin{array}{l}
\left\{ \begin{array}{l}
MA = 20\left( {cm} \right)\\
\lambda  = 3\left( {cm} \right)
\end{array} \right. \Rightarrow MA = 17\left( {cm} \right)\\
\left\{ \begin{array}{l}
M{H^2} = M{A^2} - {\left( {\frac{{AB}}{2} + x} \right)^2}\\
M{H^2} = M{B^2} - {\left( {\frac{{AB}}{2} - x} \right)^2}
\end{array} \right.
\end{array}\)

+ Từ (1) và (2), ta có:

\({20^2} + {\left( {10 + x} \right)^2} = {17^2} + {\left( {10 - x} \right)^2}\) 

=> x = 2,775(cm)

 Ta có:  

\(\begin{array}{l}
 + C = a.\varphi  + b\\
 \Rightarrow \frac{{{C_2} - {C_0}}}{{{C_1} - {C_0}}} = \frac{{{\varphi _2} - {\varphi _0}}}{{{\varphi _1} - {\varphi _0}}}\frac{{{C_2} - {C_0}}}{{{C_1} - {C_0}}} = \frac{{{\varphi _2}}}{{{\varphi _1}}}\\
 + f = \frac{1}{{2\pi \sqrt {LC} }} \Rightarrow C = \frac{1}{{4{\pi ^2}L{f^2}}}\\
 \Rightarrow \frac{{{C_2} - {C_0}}}{{{C_1} - {C_0}}} = \frac{{\frac{1}{{f_2^2}} - \frac{1}{{f_0^2}}}}{{\frac{1}{{f_1^2}} - \frac{1}{{f_0^2}}}} = \frac{{\frac{9}{{f_0^2}} - \frac{1}{{f_0^2}}}}{{\frac{4}{{f_0^2}} - \frac{1}{{f_0^2}}}} = \frac{8}{3}\\
 \Rightarrow \frac{{{\varphi _2}}}{{{\varphi _1}}} = \frac{8}{3}
\end{array}\)

+ Ta có:

\(\left\{ \begin{array}{l}
\overline \lambda   = \frac{{\overline i .\overline a }}{{\overline D }} = \frac{{0,80.1,50}}{{2,40}} = 0,50\left( {\mu m} \right)\\
\frac{{\Delta \lambda }}{{\overline \lambda  }} = \frac{{\Delta i}}{{\overline i }} + \frac{{\Delta D}}{{\overline D }} + \frac{{\Delta a}}{{\overline a }} \Rightarrow \Delta \lambda  = \overline \lambda  \left( {\frac{{\Delta i}}{{\overline i }} + \frac{{\Delta D}}{{\overline D }} + \frac{{\Delta a}}{{\overline a }}} \right) = 0,03\left( {\mu m} \right)
\end{array} \right.\) 

+ Kết quả phép đo λ được viết như sau:

\(\lambda  = \overline \lambda   + \Delta \lambda  = 0,50 \pm 0,03\left( {\mu m} \right)\)

Ta có:

\(\varepsilon  = \frac{{hc}}{\lambda } = A + \frac{1}{2}m{v^2} \Rightarrow v \approx {4.10^6}\left( {m/s} \right)\)

Để electron chuyển động thẳng đều thì lực điện và lực từ (lực Lo-ren-xơ) phải cân bằng, do đó:

\({F_d} = {F_t} \Leftrightarrow \left| q \right|E = Bv\left| q \right| \Rightarrow E = Bv = 201,4\left( {V/m} \right)\)

+ Khi f = f₁ = 50 Hz thì u_C vuông pha với u => u cùng pha với i

\( \Rightarrow {\omega _1} = \frac{1}{{\sqrt {LC} }} = 100\pi  = {\omega _R}\) 

+ Khi f₂ = 30 Hz và f₃ = 40 Hz thì U_C cho cùng một giá trị nên:

 \(\begin{array}{l}
\omega _2^2 + \omega _3^2 = 2\omega _C^2 \Rightarrow {\omega _C} = \frac{{100\pi }}{{\sqrt 2 }}\left( {rad/s} \right)\\
\omega _R^2 = {\omega _L}.{\omega _C} \Rightarrow {\omega _L} = \frac{{{{\left( {100\pi } \right)}^2}}}{{\frac{{100\pi }}{{\sqrt 2 }}}} = 100\pi \sqrt 2 \left( {rad/s} \right)
\end{array}\)

+ Khi f₀ thì U_C = max nên:

\({U_{C\max }} = {U_1} = \frac{U}{{\sqrt {1 - {{\left( {\frac{{{\omega _C}}}{{{\omega _L}}}} \right)}^2}} }} = \frac{{150}}{{\sqrt {1 - {{\left( {\frac{{\frac{{100\pi }}{{\sqrt 2 }}}}{{100\pi \sqrt 2 }}} \right)}^2}} }} = 173,21\left( V \right)\)

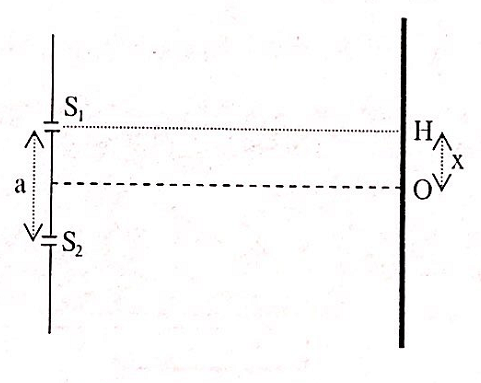
+ Lúc đầu tại H là một vân sáng nên

\({x_H} = k\frac{{\lambda D}}{a}\)                             (1)

Sau khi dịch ra xa thêm 1/7 (m) thì H thành vân tối lần thứ nhất nên k giảm đi 0,5:

\({x_H} = \left( {k - 0,5} \right)\frac{{\lambda \left( {D + \frac{1}{7}} \right)}}{a}\)         (2)

+ Dịch ra xa thêm 16/35 (m) thì H thành vân tối lần thứ 2 nên (k - 0,5) giảm đi 1:

\({x_H} = \left( {k - 1,5} \right)\frac{{\lambda \left( {D + \frac{1}{7} + \frac{{16}}{{35}}} \right)}}{a}\)   (3)

+ Từ (1), (2) và (3), ta có:  

\(\begin{array}{l}
\left\{ \begin{array}{l}
kD = \left( {k - 0,5} \right)\left( {D + \frac{1}{7}} \right)\\
kD = \left( {k - 1,5} \right)\left( {D + 0,6} \right)
\end{array} \right.\\
 \Rightarrow \left\{ \begin{array}{l}
\frac{k}{7} - 0,5D - \frac{1}{{14}} = 0\\
0,6k - 1,5D - 0,9 = 0
\end{array} \right. \Rightarrow \left\{ \begin{array}{l}
k = 4\\
D = 1\left( m \right)
\end{array} \right.\\
{x_H} = 0,5a = k\frac{{\lambda D}}{a}\\
 \Rightarrow {a^2} = 2k\lambda D \Rightarrow a = \sqrt {2.4.0,5.1}  = 2\left( {mm} \right)
\end{array}\)

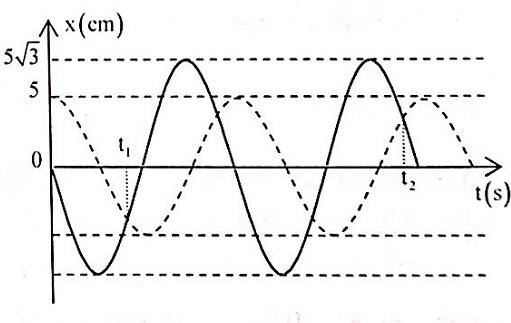
+ Cứ sau nửa chu kì thì hai chất điểm lại đi ngang qua nhau.

+ Do đó, sau n lần ngang qua nhau mất thời gian: Δt = (n - 1)T/2

+ Từ đồ thị thấy trong thời gian 3 s chúng đi qua nhau 4 lần nên:

\(\left( {4 - 1} \right)\frac{T}{2} = 3 \Rightarrow T = 2\left( s \right)\) 

+ Khoảng cách hai chất điểm theo phương dao động:

\(\Delta x = {x_2} - {x_1} = 10\cos \left( {\omega t + \frac{{2\pi }}{3}} \right)\) 

+ Trong một chu kì có 4 lần \(\left| {\Delta x} \right| = 5\sqrt 2 \left( {cm} \right)\) 

+ Ta có: 

\(\begin{array}{l}
\Delta t = \frac{T}{6} + \frac{T}{4} + \frac{T}{4} + \frac{T}{8} = \frac{{19T}}{{24}}\\
 \Rightarrow t = 503T + \frac{{19T}}{{24}} = \frac{{12091}}{{24}}T = \frac{{12091}}{{12}}\left( s \right)
\end{array}\)

Gọi P là công suất nơi phát.

+ Công suất nơi tiêu thụ lúc đầu là:

\(H = \frac{{{P_{tt}}}}{P} \Rightarrow {P_{tt}} = 0,9P\) 

+ Công suất nơi tiêu thụ lúc sau:

\(P_{tt}^/ = 0,9P.0,7 = 0,63P \Rightarrow {H^/} = \frac{{P_{tt}^/}}{P} = 0,63\) 

+ Vì cosφ = 1

\(\begin{array}{l}
 \Rightarrow H = \frac{{{U_{tt}}}}{U} = \frac{{{U_{tt}}}}{{{U_{tt}} + \Delta U}} = \frac{1}{{1 + \frac{{\Delta U}}{{{U_{tt}}}}}} \Rightarrow \frac{{\Delta U}}{{{U_{tt}}}} = \frac{1}{H} - 1\\
 \Rightarrow \frac{{\Delta {U^/}}}{{U_{tt}^/}} = \frac{1}{{{H^/}}} - 1 = \frac{1}{{0,63}} - 1 = \frac{{37}}{{63}}
\end{array}\)