Các ánh sáng đơn sắc ứng với tần số tương ứng tăng dần: Cam, lục, chàm, tím. 

Trong máy phát điện tùy thuộc vào cấu tạo của máy, phần cảm và phần ứng có thể là bộ phận chuyển động hoặc là bộ phận đứng yên.

Tia Rơn-ghen (tia X) có cùng bản chất với tia tử ngoại.

Trong hạt nhân nguyên tử số khối A chính là tổng số các nuclôn.   

Điều kiện để phản ứng dây chuyền xảy ra là \(k\ge 1.\)

Chu kì dao động riêng của mạch là \(T=2\pi \sqrt{LC}.\)

Vì siêu âm mang bản chất là sóng cơ học nên siêu âm không thể truyền được trong chân không.

Biên độ của con lắc đơn là\({{S}_{0}}=1\left( dm \right)=10\left( cm \right).\)

Khoảng cách giữa hai ngọn sóng liên tiếp là\(\lambda =1\left( m \right).\)

Pha của dòng điện ở thời điểm t là\(\omega t+\varphi =100\pi t\left( rad \right).\)

Số vạch quang phổ phát xạ của nguyên tử hiđrô là\(C_{n}^{2}=6\Rightarrow n=4\) (quỹ đạo N).

Gọi số photon của đèn phát ra trong 1s là n.

\(P=n\varepsilon =n\frac{hc}{\lambda }\Rightarrow 1=n\frac{{{6,625.10}^{-34}}{{.3.10}^{8}}}{{{0,7.10}^{-6}}}\Rightarrow n={{3,52.10}^{18}}\)(hạt).

Ta có:

\(A=qU\Rightarrow {{0,2.10}^{-3}}={{1.10}^{-6}}U\Rightarrow U=200\left( V \right).\)

Tần số dao động của vật là:

\(f=\frac{1}{2\pi }\sqrt{\frac{k}{m}}=\frac{1}{2\pi }\sqrt{\frac{1000}{1}}=5\left( Hz \right)\)

Ta có:

\(T=2\pi \sqrt{\frac{\ell }{g}}\Rightarrow \frac{{{T}'}}{T}=\sqrt{\frac{{{\ell }'}}{\ell }}=\sqrt{1,44}=1,2\Rightarrow {T}'=1,2T=1,2.1,5=1,8\left( s \right).\)

Trên dây có 5 nút sóng\(\Rightarrow n=4.\)

\(\ell =n\frac{\lambda }{2}\Rightarrow 1,2=4\frac{\lambda }{2}\Rightarrow \lambda =0,6\left( m \right).\)

Ta có:

\({{Z}_{RL}}=\frac{{{U}_{0}}}{{{I}_{0}}}=\frac{100}{\sqrt{2}}=50\sqrt{2}\left( \Omega  \right)\left( 1 \right)\); \(\tan {{\varphi }_{{}^{u}/{}_{i}}}=\frac{{{Z}_{L}}}{R}=\tan \frac{\pi }{4}=1\Rightarrow {{Z}_{L}}=R\left( 2 \right).\)

Từ \(\left( 1 \right),\left( 2 \right)\Rightarrow R={{Z}_{L}}=50\left( \Omega  \right)\Rightarrow L=\frac{{{Z}_{L}}}{\omega }=\frac{1}{2\pi }\left( H \right).\)

\({{\text{W}}_{PT}}=\left( \Delta {{m}_{X}}-2\Delta {{m}_{D}} \right){{c}^{2}}=\left( 0,0083-2.0,0024 \right).931\approx 3,26\left( MeV \right)\)

\(\Rightarrow \)Phản ứng tỏa năng lượng là 3,26(MeV).

Các bức xạ có bước sóng trong khoảng từ\({{3.10}^{-9}}m\)đến\({{3.10}^{-7}}m\)là tia tử ngoại.   

Phát biểu nào sau đây là đúng: Âm tần và cao tần cùng là sóng điện từ nhưng tần số âm tần nhỏ hơn tần số cao tần.    

Công suất tiêu thụ điện hữu ích tăng.  

\(T=\frac{2\pi }{\omega }=\frac{2\pi }{10\pi }=0,2\left( s \right)\Rightarrow \lambda =vT=20.0,2=4\left( cm \right).\)

Có: \({{d}_{2}}-{{d}_{1}}=-10=-2,5\lambda \Rightarrow \)là cực tiểu thứ 3 gần về phía A (do\(AN<BN\)).

Vận tốc tại vị trí cân bằng là\(v={{v}_{\max }}=\omega A=10A=100\left( {cm}/{s}\; \right)\Rightarrow A=10\left( cm \right)\)

\(\Delta \varphi =\frac{\pi }{4}-\left( -\frac{3\pi }{4} \right)=\pi \left( rad \right)\Rightarrow \)Hai dao động \({{x}_{1}},{{x}_{2}}\)ngược pha.

\(\Rightarrow A=\left| {{A}_{1}}-{{A}_{2}} \right|\Rightarrow 10=\left| 5-{{A}_{2}} \right|\Rightarrow {{A}_{2}}=15\left( cm \right).\)

Ta có:

\({{\text{W}}_{LKR\left( S \right)}}=\frac{270}{32}=8,4375\left( {MeV}/{nuclon}\; \right);{{\text{W}}_{LKR\left( Cr \right)}}=\frac{447}{52}=8,5962\left( {MeV}/{nuclon}\; \right).\)

\({{\text{W}}_{LKR\left( U \right)}}=\frac{1785}{238}=7,5\left( {MeV}/{nuclon}\; \right)\)

\(\Rightarrow {{\text{W}}_{LKR\left( U \right)}}<{{\text{W}}_{LKR\left( S \right)}}<{{\text{W}}_{LKR\left( Cr \right)}}\)

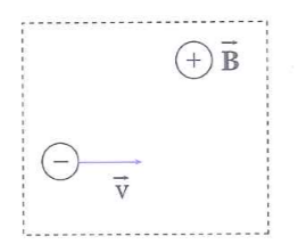
Electron có hai lực tác dụng \(\overrightarrow{{{F}_{d}}},\overrightarrow{{{F}_{L}}};\overrightarrow{{{F}_{L}}}\)hướng xuống (theo quy tắc bàn tay trái).

Electron chuyển động đều

\( \Rightarrow \overrightarrow {{F_d}}  + \overrightarrow {{F_L}}  = \vec 0 \Rightarrow \left\{ \begin{array}{l}
\overrightarrow {{F_d}}  \uparrow  \downarrow \overrightarrow {{F_L}} \left( 1 \right)\\
{F_d} = {F_L}\left( 2 \right)
\end{array} \right.\)

\(\left( 1 \right)\Rightarrow \overrightarrow{{{F}_{d}}}\)có chiều hướng lên,\({{q}_{e}}<0\Rightarrow \overrightarrow{E}\) hướng xuống.

\(\left( 2 \right)\Rightarrow \left| q \right|E=\left| q \right|vB\sin \alpha \Rightarrow E=vB={{2.10}^{6}}.0,004=8000\left( {V}/{m}\; \right).\)

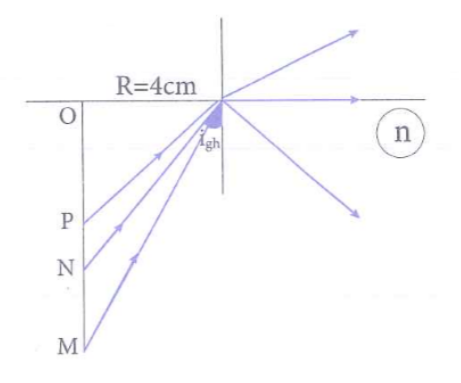
Khi độ dài đoạn OA giảm dần thì góc tới của tia sáng xuất phát từ A tới mép miếng gỗ càng tăng.

Ta có mắt bắt đầu không nhìn thấy A khi A trùng N là điểm cho góc tới mép miếng gỗ bằng góc giới hạn.

\(\sin {{i}_{gh}}=\frac{{{n}_{2}}}{{{n}_{1}}}=\frac{1}{1,33}\Rightarrow {{i}_{gh}}\approx 48,6{}^\circ \)

\(\tan {{i}_{gh}}=\frac{R}{ON}\Rightarrow ON=\frac{R}{\tan {{i}_{gh}}}\approx 3,53cm\)

Sơ đồ mạch điện R₁ nt (R₂ // Đ)

Có\({{R}_{\text{ }\!\!\S\!\!\text{ }}}=\frac{U_{dm}^{2}}{{{P}_{dm}}}=\frac{{{6}^{2}}}{3}=12\left( \Omega  \right);{{I}_{dm}}=\frac{{{P}_{dm}}}{{{U}_{dm}}}=\frac{3}{6}=\frac{1}{2}\left( A \right)\)

Vì đèn sáng bình thường\(\Rightarrow {{U}_{\text{ }\!\!\S\!\!\text{ }}}={{U}_{dm}}=6\left( V \right)={{U}_{2}};{{I}_{\text{ }\!\!\S\!\!\text{ }}}={{I}_{dm}}=\frac{1}{2}\left( A \right)\)

Đặt\({{R}_{2}}=x\Rightarrow {{I}_{2}}=\frac{{{U}_{2}}}{{{R}_{2}}}=\frac{6}{x}\left( A \right)\Rightarrow {{I}_{1}}={{I}_{2}}+{{I}_{\text{ }\!\!\S\!\!\text{ }}}=\frac{1}{2}+\frac{6}{x}\left( A \right)=I\)

\({{U}_{AB}}=\) E\(-Ir={{U}_{1}}+{{U}_{2}}\)

\(\Rightarrow 12-\left( \frac{1}{2}+\frac{6}{x} \right).1=\left( \frac{1}{2}+\frac{6}{x} \right).5+6\)

Đặt \(t=\frac{1}{2}+\frac{6}{x}\Rightarrow \)Ta có phương trình\(12-t=5t+6\Rightarrow t=1\Rightarrow \frac{1}{2}+\frac{6}{x}=1\Rightarrow x=12\)

Vậy\({{R}_{2}}=12\left( \Omega  \right)\)

Từ đồ thị ta có\(\Delta t=\frac{13}{6}-\frac{7}{6}=1\left( s \right)=\frac{T}{2}\Rightarrow T=2\left( s \right)\Rightarrow \omega =\frac{2\pi }{T}=\pi \left( {rad}/{s}\; \right)\)

\({{F}_{kv\max }}=m{{\omega }^{2}}A=0,1{{\pi }^{2}}A={{4.10}^{-2}}\left( N \right)\Rightarrow A=4\left( cm \right)\)

Tại\(t=0:{{F}_{kv}}=-m{{\omega }^{2}}A=-{{2.10}^{-2}}\Rightarrow x=2\left( cm \right)\)

\({{F}_{kv}}\)tăng \(\Rightarrow \)x giảm \(\Rightarrow \)vật đang chuyển động về vị trí cân bằng

\(\Rightarrow v<0\Rightarrow \varphi >0\Rightarrow \varphi =\arccos \frac{x}{A}=\arccos \frac{2}{4}=\frac{\pi }{3}\left( rad \right)\)

Vậy phương trình dao động của vật là\(x=4\cos \left( \pi t+\frac{\pi }{3} \right)\left( cm \right)\)

Ta có:

\(P=\frac{{{U}^{2}}.R}{{{R}^{2}}+{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}}=\frac{{{U}^{2}}.{{R}^{2}}}{R.{{Z}^{2}}}=\frac{{{U}^{2}}}{R}{{\cos }^{2}}\varphi \)

\({{P}_{1}}=60\left( \text{W} \right)=\frac{{{U}^{2}}}{{{R}_{1}}}{{\cos }^{2}}{{\varphi }_{1}}\Rightarrow \frac{{{100}^{2}}}{50}{{\cos }^{2}}{{\varphi }_{1}}=60\Rightarrow {{\cos }^{2}}{{\varphi }_{1}}=\frac{3}{10}\)

\({{\cos }^{2}}{{\varphi }_{1}}+{{\cos }^{2}}{{\varphi }_{2}}=\frac{3}{4}\Rightarrow {{\cos }^{2}}{{\varphi }_{2}}=\frac{9}{20}\Rightarrow {{P}_{2}}=\frac{{{U}^{2}}}{{{R}_{2}}}{{\cos }^{2}}{{\varphi }_{2}}=\frac{{{100}^{2}}}{25}.\frac{9}{20}=180\left( \text{W} \right)\)

Vậy\(\frac{{{P}_{2}}}{{{P}_{1}}}=\frac{180}{60}=3.\)

Gọi số vòng dây cuộn sơ cấp của hai máy là N.

Số vòng dây cuộn thứ cấp của máy 1 là N₁, cuộn thứ cấp của máy 2 là N₂.

Có:\(\frac{{{N}_{1}}}{N}=\frac{{{U}_{1}}}{U}=1,5\Rightarrow {{N}_{1}}=1,5N;\frac{{{N}_{2}}}{N}=\frac{{{U}_{2}}}{U}=1,8\Rightarrow {{N}_{2}}=1,8N\)

Để tỉ số điện áp của hai máy như nhau thì số vòng dây cuộn sơ cấp của máy 1 giảm đi 20 vòng, số vòng dây cuộn sơ cấp của máy 2 tăng thêm 20 vòng.

\(\Rightarrow \frac{{{N}_{1}}}{N-20}=\frac{{{N}_{2}}}{N+20}\Rightarrow \frac{1,5N}{N-20}=\frac{1,8N}{N+20}\Rightarrow 0,3{{N}^{2}}-66N=0\Rightarrow N=220\)(vòng).

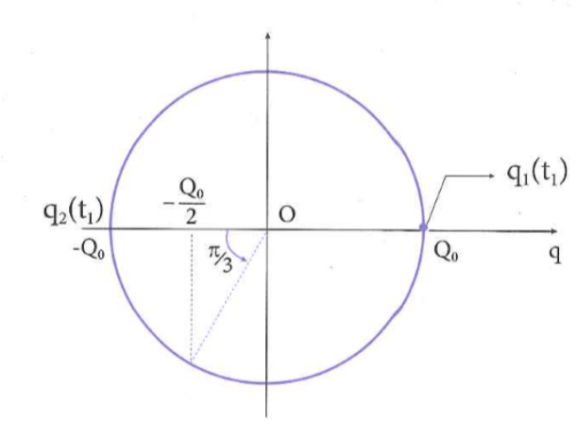
Ta có:

\({{t}_{1}}=0:{{q}_{1}}={{Q}_{0}}\Rightarrow {{q}_{2}}=-{{Q}_{0}}\)

\({{t}_{2}}={{10}^{-6}}s:{{q}_{2}}=-\frac{{{Q}_{0}}}{2}\Rightarrow \alpha =\frac{\pi }{3}\)

\(\omega =\frac{2\pi }{T}=\frac{\alpha }{\Delta t}\Rightarrow T={{6.10}^{-6}}s\)

Ta có:

\({{x}_{M}}=\frac{k\lambda D}{a}=\frac{{{k}_{1}}\lambda D}{a+\Delta a}=\frac{{{k}_{2}}\lambda D}{a-\Delta a}\)

\(\Rightarrow \frac{k}{a}=\frac{{{k}_{1}}}{a+\Delta a}=\frac{{{k}_{2}}}{a-\Delta a}=\frac{{{k}_{1}}+{{k}_{2}}}{a+\Delta a+a-\Delta a}=\frac{{{k}_{1}}+{{k}_{2}}}{2a}\)

\(\Rightarrow 2k={{k}_{1}}+{{k}_{2}}\)

Ta có:

\(\varepsilon =\frac{hc}{\lambda }={{A}_{0}}+{{\text{W}}_{d}}={{A}_{0}}+\frac{1}{2}m{{v}^{2}}\left( 1 \right)\)

Electron có vận tốc cực đại khi bước sóng chiếu tới nhỏ nhất

Thay \(\lambda =400nm\)vào (1) ta có:

\(v=\sqrt{\frac{2\left( \frac{hc}{\lambda }-{{A}_{0}} \right)}{m}}=\sqrt{\frac{2\left( \frac{{{6,625.10}^{-34}}{{.3.10}^{8}}}{{{400.10}^{-9}}}-{{3,31.10}^{-19}} \right)}{{{9,1.10}^{-31}}}}\approx {{0,6.10}^{6}}\left( {m}/{s}\; \right)\)

Ta có số phôtôn chiếu vào quang trở trong một giây là

\({{n}_{\varepsilon }}=\frac{P}{\varepsilon }=\frac{P}{\frac{hc}{\lambda }}=\frac{P\lambda }{hc}=\frac{{{30.0,8.10}^{-6}}}{{{6,625.10}^{-34}}{{.3.10}^{8}}}\approx {{1,21.10}^{20}}\) hạt

Cường độ dòng điện chạy qua quang trở khi bóng đèn sáng bình thường là

\({{I}_{qt}}={{I}_{d}}={{I}_{dm}}=\frac{{{P}_{dm}}}{{{U}_{dm}}}=\frac{3}{6}=0,5A.\)

Số electron nhận được photon và rời khỏi mối liên kết là

\({{n}_{e}}={{n}_{lotrong}}=\frac{I}{2.e}=\frac{0,5}{{{2.1,6.10}^{-19}}}={{1,5625.10}^{18}}\)hạt.

Hiệu suất của quá trình lượng tử là

\(H=\frac{{{n}_{e}}}{{{n}_{\varepsilon }}}=\frac{{{1,5625.10}^{18}}}{{{1,21.10}^{20}}}.100%\approx 1,3%.\)

Ta có\({{N}_{Pb}}={{N}_{0}}-{{N}_{t}}\)

\(\frac{{{m}_{U}}}{{{m}_{Pb}}}=37\Rightarrow \frac{238\frac{{{N}_{t}}}{{{N}_{A}}}}{206\frac{{{N}_{0}}-{{N}_{t}}}{{{N}_{A}}}}=37\Rightarrow \frac{{{N}_{t}}}{{{N}_{0}}-{{N}_{t}}}=\frac{3811}{119}\)

\(\Rightarrow {{N}_{t}}=\frac{3811}{3930}{{N}_{0}}={{N}_{0}}{{.2}^{-\frac{t}{T}}}\Rightarrow t\approx {{2.10}^{8}}\)(năm).

Ống nghiệm có một đầu là nước, một đầu hở

\(\Rightarrow \ell =\frac{\lambda }{4}+n\frac{\lambda }{2}=\frac{v}{4f}+n\frac{v}{2f}\Rightarrow v=\frac{\ell }{\frac{1}{4f}+\frac{n}{2f}}\)

\(300<v<350\Rightarrow 300<\frac{0,5}{\frac{1}{4.850}+\frac{n}{2.850}}<350\Rightarrow \frac{27}{14}<n<\frac{7}{3}\)

mà \(n\in \mathbb{N}\Rightarrow n=2\Rightarrow v=340\left( {m}/{s}\; \right)\)

Tiếp tục đổ thêm nước\(\Rightarrow 0<\ell <0,5\left( m \right)\Rightarrow 0<\frac{340}{4.850}+\frac{n.340}{2.850}<0,5\Rightarrow -0,5<n<2\)

\(n\in \mathbb{N}\Rightarrow n\in \left\{ 0;1 \right\}\)

Vậy khi tiếp tục đổ thêm nước thì có thêm 2 vị trí của mực nước mà âm khuếch đại rất mạnh.

\({{x}_{lam1}}=\frac{{{\lambda }_{lam}}D}{a}=\frac{{{0,45.10}^{-6}}.2}{{{1.10}^{-3}}}=0,9\left( mm \right);{{x}_{cam1}}=\frac{{{\lambda }_{cam}}D}{a}=\frac{{{0,45.10}^{-6}}.2}{{{1.10}^{-3}}}=1,3\left( mm \right)\)

Quang phổ bậc 1:\({{x}_{1}}\in \left( 0,9;1,3 \right)mm\)

Quang phổ bậc 2:\({{x}_{2}}\in \left( 1,8;2,6 \right)mm\)

Quang phổ bậc 3:\({{x}_{3}}\in \left( 2,7;3,9 \right)mm\)

Quang phổ bậc 4:\({{x}_{4}}\in \left( 3,6;5,2 \right)mm\)

\(\Rightarrow \)Từ quang phổ bậc 4 trở đi sẽ có vùng giao với quang phổ bậc thấp hơn.

\(\Rightarrow \)Khoảng rộng nhỏ nhất không có vân sáng nào\(\Delta {{x}_{\min }}={{x}_{lam3}}-{{x}_{cam2}}=2,7-2,6=0,1\left( mm \right)\)

Có:\(T=2\pi \sqrt{\frac{\ell }{g}}\Rightarrow T\sim \frac{1}{\sqrt{g}}\)

\(\frac{{{T}_{1}}}{{{T}_{0}}}=5\Rightarrow \sqrt{\frac{g}{{{g}_{1}}}}=5\Rightarrow {{g}_{1}}=\frac{g}{25}\)mà \(\overrightarrow{E}\)hướng thẳng đứng xuống dưới\(\Rightarrow {{g}_{1}}=g-{{g}_{\text{l }\!\!{}^\text{1}\!\!\text{ 1}}}\left( \overrightarrow{{{g}_{\text{l }\!\!{}^\text{1}\!\!\text{ 1}}}}\uparrow \downarrow \overrightarrow{g} \right)\)

\(\Rightarrow {{g}_{\text{l }\!\!{}^\text{1}\!\!\text{ 1}}}=\frac{24g}{25}=\frac{\left| {{q}_{1}}E \right|}{m};{{q}_{1}}<0\) do \(\overrightarrow{E}\uparrow \downarrow \overrightarrow{{{g}_{\text{l }\!\!{}^\text{1}\!\!\text{ 1}}}}\)                (1)

\(\frac{{{T}_{2}}}{{{T}_{0}}}=\frac{5}{7}\Rightarrow \sqrt{\frac{g}{{{g}_{2}}}}=\frac{5}{7}\Rightarrow {{g}_{2}}=\frac{49}{25}g\)

mà \(\overrightarrow{E}\)hướng thẳng đứng xuống dưới\(\Rightarrow {{g}_{2}}=g+{{g}_{\text{l }\!\!{}^\text{1}\!\!\text{ 2}}}\left( \overrightarrow{{{g}_{\text{l }\!\!{}^\text{1}\!\!\text{ 2}}}}\uparrow \uparrow \overrightarrow{g} \right)\)

\(\Rightarrow {{g}_{\text{l }\!\!{}^\text{1}\!\!\text{ 2}}}=\frac{24g}{25}=\frac{\left| {{q}_{2}}E \right|}{m};{{q}_{2}}>0\) do \(\overrightarrow{E}\uparrow \uparrow \overrightarrow{{{g}_{\text{l }\!\!{}^\text{1}\!\!\text{ 2}}}}\)                (2)

\(\left( 1 \right),\left( 2 \right)\Rightarrow {{g}_{\text{l }\!\!{}^\text{1}\!\!\text{ 1}}}={{g}_{\text{l }\!\!{}^\text{1}\!\!\text{ 2}}}\Rightarrow \left| {{q}_{1}} \right|=\left| {{q}_{2}} \right|\) mà \({{q}_{1}},{{q}_{2}}\)trái dấu \(\Rightarrow \frac{{{q}_{1}}}{{{q}_{2}}}=-1\)

Bước sóng là\(\lambda =\frac{v}{f}=\frac{v.2\pi }{\omega }=2cm.\)

Phương trình sóng tại M \({{u}_{M}}=2.1,5\cos \left( 20\pi t+{}^{\pi }/{}_{6}-\frac{2\pi d}{\lambda } \right)\)

M cùng pha với nguồn \(\Leftrightarrow \Delta \varphi =\frac{2\pi d}{\lambda }=k2\pi \Rightarrow d=k\lambda \)mà\(d>10\Rightarrow k>5\)

Mà M gần O nhất nên\({{k}_{\min }}=6\Rightarrow {{d}_{\min }}=12\Rightarrow O{{M}_{\min }}=2\sqrt{11}cm\)

O và N là 2 điểm cực đại gần nhau trên đoạn thẳng nối 2 nguồn nên\(ON=\frac{\lambda }{2}=1cm.\)

Ta có phương trình dao động của hai chất điểm M và N là

\({{u}_{M}}=3\cos \left( 20\pi t+{}^{\pi }/{}_{6}-12\pi  \right)=3\cos \left( 20\pi t+{}^{\pi }/{}_{6} \right)\)

\({{u}_{N}}=2.1,5\cos \left( \pi \frac{{{d}_{2}}-{{d}_{1}}}{\lambda } \right)\cos \left( 20\pi t+{}^{\pi }/{}_{6}-\pi \frac{{{d}_{1}}+{{d}_{2}}}{\lambda } \right)\)

\(=3\cos \left( \pi  \right)\cos \left( 20\pi t+{}^{\pi }/{}_{6}-10\pi  \right)\)

\(=-3\cos \left( 20\pi t+{}^{\pi }/{}_{6} \right)\)

Khoảng cách theo phương thẳng đứng giữa M và N là

\(\left| {{u}_{M}}-{{u}_{N}} \right|=\left| 3\cos \left( 20\pi t+{}^{\pi }/{}_{6} \right)-\left( -3\cos \left( 20\pi t+{}^{\pi }/{}_{6} \right) \right) \right|=\left| 6\cos \left( 20\pi t+{}^{\pi }/{}_{6} \right) \right|\)

Vậy khoảng cách lớn nhất giữa M và N trong quá trình dao động là

\(M{{N}_{\max }}=\sqrt{{{\left( 2\sqrt{11} \right)}^{2}}+{{1}^{2}}+{{6}^{2}}}=9cm\)

Từ đồ thị ta có\(\frac{T}{4}={{10.10}^{-3}}s\Rightarrow T=0,04s\Rightarrow \omega =\frac{2\pi }{T}=50\pi \left( {rad}/{s}\; \right)\)

Tại\(t=0\)

\({{u}_{AM}}={{U}_{0AM}}=200\left( V \right)\Rightarrow {{\varphi }_{{{u}_{AM}}}}=0\Rightarrow {{u}_{AM}}=200\cos \left( 50\pi t \right)\left( V \right)\)

\({{u}_{MB}}=0;{{u}_{MB}}\)giảm \(\Rightarrow {{\varphi }_{{{u}_{MB}}}}=\frac{\pi }{2}\left( rad \right)\Rightarrow {{u}_{MB}}=200\cos \left( 50\pi t+\frac{\pi }{2} \right)\left( V \right)\)

Từ đồ thị ta có phương trình của hiệu điện thế hai đầu mạch AM và MB là

\(\Rightarrow {{u}_{AB}}={{u}_{AM}}+{{u}_{MB}}=200\sqrt{2}\cos \left( 50\pi t+\frac{\pi }{4} \right)\left( V \right)\)

Ta thấy \(t=0\) có \(i={}^{{{I}_{0}}}/{}_{\sqrt{2}}\)và đang giảm nên\(\Rightarrow {{\varphi }_{i}}=\frac{\pi }{4}\)

Như vậy trong mạch lúc này đang có cộng hưởng điện\(\Rightarrow {{Z}_{L}}={{Z}_{C}}\)

\({{U}_{0AM}}={{U}_{0MB}}\Rightarrow \sqrt{{{R}^{2}}+{{Z}_{C}}^{2}}=\sqrt{{{r}^{2}}+{{Z}_{L}}^{2}}\)

\({{\varphi }_{{{u}_{{}^{AM}/{}_{i}}}}}=-\frac{\pi }{4}\Rightarrow R={{Z}_{C}}=\frac{1}{C\omega }=100\Omega \)

\(\Rightarrow R=r={{Z}_{C}}=100\Omega \)

\(P=\frac{{{U}^{2}}}{R+r}=\frac{{{200}^{2}}}{100+100}=200\text{W}\)