Hoành độ giao điểm của hai đồ thị hàm số là nghiệm của pt:

\(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaaca % WG4bWaaWbaaSqabeaacaaIYaaaaOGaeyOeI0IaaGymaaqaaiaadIha % cqGHRaWkcaaIYaaaaiabg2da9iaaikdacaWG4bGaeyOeI0YaaSaaae % aacaaIXaGaaG4maaqaaiaaisdaaaGaeyi1HS9aaiqaaqaabeqaaiaa % dIhacqGHGjsUcqGHsislcaaIYaaabaGaeyOeI0IaaGinaiaadIhada % ahaaWcbeqaaiaaikdaaaGccqGHsislcaaIZaGaamiEaiabgUcaRiaa % ikdacaaIYaGaeyypa0JaaGimaaaacaGL7baacqGHuhY2daGabaabae % qabaGaamiEaiabgcMi5kabgkHiTiaaikdaaeaadaWabaabaeqabaGa % amiEaiabg2da9iaaikdaaeaacaWG4bGaeyypa0JaeyOeI0IaaGPaVp % aalaaabaGaaGymaiaaigdaaeaacaaI0aaaaaaacaGLBbaaaaGaay5E % aaGaeyi1HS9aamqaaqaabeqaaiaadIhacqGH9aqpcaaIYaaabaGaam % iEaiabg2da9iabgkHiTiaaykW7daWcaaqaaiaaigdacaaIXaaabaGa % aGinaaaaaaGaay5waaaaaa!73B4! \frac{{{x^2} - 1}}{{x + 2}} = 2x - \frac{{13}}{4} \Leftrightarrow \left\{ \begin{array}{l} x \ne - 2\\ - 4{x^2} - 3x + 22 = 0 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} x \ne - 2\\ \left[ \begin{array}{l} x = 2\\ x = - \,\frac{{11}}{4} \end{array} \right. \end{array} \right. \Leftrightarrow \left[ \begin{array}{l} x = 2\\ x = - \,\frac{{11}}{4} \end{array} \right.\)

\(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGabmyEayaafa % Gaeyypa0ZaaSaaaeaacaaIZaaabaWaaeWaaeaacqGHsislcaWG4bGa % ey4kaSIaaGymaaGaayjkaiaawMcaamaaCaaaleqabaGaaGOmaaaaaa % GccqGH+aGpcaaIWaGaaGPaVlaaysW7cqGHaiIicaWG4bGaeyiyIKRa % aGymaiabgkDiEpaaxababaGaciyBaiaacMgacaGGUbaaleaadaWada % qaaiaaikdacaGG7aGaaG4maaGaay5waiaaw2faaaqabaGccaWG5bGa % eyypa0JaamyEamaabmaabaGaaGOmaaGaayjkaiaawMcaaiabg2da9i % abgkHiTiaaiwdaaaa!5991! y' = \frac{3}{{{{\left( { - x + 1} \right)}^2}}} > 0\,\;\forall x \ne 1 \Rightarrow \mathop {\min }\limits_{\left[ {2;3} \right]} y = y\left( 2 \right) = - 5\)

Xác suất 2 người được chọn đều là nữ là \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaaca % WGdbWaa0baaSqaaiaaiodaaeaacaaIYaaaaaGcbaGaam4qamaaDaaa % leaacaaIXaGaaGimaaqaaiaaikdaaaaaaOGaeyypa0ZaaSaaaeaaca % aIXaaabaGaaGymaiaaiwdaaaaaaa!3EF7! \frac{{C_3^2}}{{C_{10}^2}} = \frac{1}{{15}}\)

\(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaaeaaaaaaaaa8 % qaciGGJbGaai4BaiaacohacaWG4bGaeyypa0JaeyOeI0IaaGPaVlaa % cckadaWcaaqaaiaaigdaaeaacaaIYaaaaiabgsDiBlGacogacaGGVb % Gaai4CaiaadIhacqGH9aqpciGGJbGaai4BaiaacohadaWcaaqaaiaa % ikdacqaHapaCaeaacaaIZaaaaiabgsDiB-aacaWG4bGaeyypa0Jaey % ySae7aaSaaaeaacaaIYaGaeqiWdahabaGaaG4maaaacqGHRaWkcaWG % RbGaaGOmaiabec8aWjaacYcacaWGRbGaeyicI4SaeSijHikaaa!5FE0! \cos x = - \,\;\frac{1}{2} \Leftrightarrow \cos x = \cos \frac{{2\pi }}{3} \Leftrightarrow x = \pm \frac{{2\pi }}{3} + k2\pi ,k \in \)

\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGabmyEayaafa % Gaeyypa0JaamiEamaaCaaaleqabaGaaG4maaaakiabgUcaRiaadIha % cqGHshI3ceWG5bGbauaadaqadaqaaiabgkHiTiaaigdaaiaawIcaca % GLPaaacqGH9aqpcqGHsislcaaIYaaaaa!451B! y' = {x^3} + x \Rightarrow y'\left( { - 1} \right) = - 2\)

Hàm số \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9iGacohacaGGPbGaaiOBaiaadIhaaaa!3BCD! y = \sin x\) tuần hoàn với chu kì \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaaGOmaiabec % 8aWbaa!386D! 2\pi \).

\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaeWaaeaaca % WGibaacaGLOaGaayzkaaGaeyykICSaam4taiaadIhaaaa!3BB9! \left( H \right) \cap Ox\)\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyO0H4Taam % yEaiabg2da9iaaicdaaaa!3B0F! \Rightarrow y = 0\)\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyO0H4Taam % iEaiabg2da9iaaikdaaaa!3B10! \Rightarrow x = 2\)\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyqamaabm % aabaGaaGOmaiaacUdacaaIWaaacaGLOaGaayzkaaaaaa!3A78! A\left( {2;0} \right)\)

\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGabmyEayaafa % Gaeyypa0ZaaSaaaeaacqGHsislcaaIYaaabaWaaeWaaeaacaWG4bGa % eyOeI0IaaG4maaGaayjkaiaawMcaamaaCaaaleqabaGaaGOmaaaaaa % aaaa!3ED6! y' = \frac{{ - 2}}{{{{\left( {x - 3} \right)}^2}}}\)\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyO0H4Tabm % yEayaafaWaaeWaaeaacaaIYaaacaGLOaGaayzkaaGaeyypa0JaeyOe % I0IaaGOmaaaa!3E4F! \Rightarrow y'\left( 2 \right) = - 2\)

Phương trình tiếp tuyến: \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9iabgkHiTiaaikdadaqadaqaaiaadIhacqGHsislcaaIYaaacaGL % OaGaayzkaaaaaa!3DD0! y = - 2\left( {x - 2} \right)\)\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyi1HSTaam % yEaiabg2da9iabgkHiTiaaikdacaWG4bGaey4kaSIaaGinaaaa!3E9A! \Leftrightarrow y = - 2x + 4\)

\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGabmOzayaafa % WaaeWaaeaacaWG4baacaGLOaGaayzkaaGaeyypa0ZaaSaaaeaacaaI % YaGaaiOlaiaaigdacqGHsislcaaIXaWaaeWaaeaacqGHsislcaaIXa % aacaGLOaGaayzkaaaabaWaaeWaaeaacaWG4bGaey4kaSIaaGymaaGa % ayjkaiaawMcaamaaCaaaleqabaGaaGOmaaaaaaGccqGH9aqpdaWcaa % qaaiaaiodaaeaadaqadaqaaiaadIhacqGHRaWkcaaIXaaacaGLOaGa % ayzkaaWaaWbaaSqabeaacaaIYaaaaaaaaaa!4D7E! f'\left( x \right) = \frac{{2.1 - 1\left( { - 1} \right)}}{{{{\left( {x + 1} \right)}^2}}} = \frac{3}{{{{\left( {x + 1} \right)}^2}}}\)

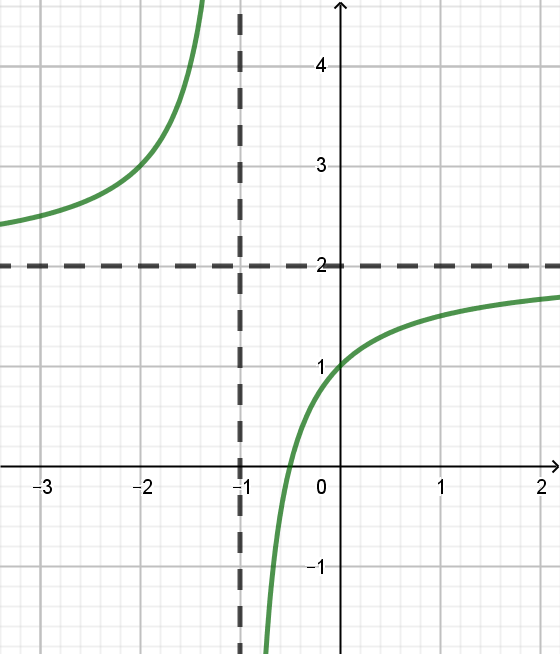
Dựa vào đồ thị trên, ta thấy đồ thị hàm số có tiệm cận đứng là đường thẳng \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiEaiabg2 % da9iabgkHiTiaaigdaaaa!399F! x = - 1\), tiệm cận ngang là đường thẳng \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9iaaikdaaaa!38B4! y = 2\).và hàm số đồng biến trên mỗi khoảng \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaeWaaeaacq % GHsislcqGHEisPcaGG7aGaaGPaVlabgkHiTiaaigdaaiaawIcacaGL % Paaaaaa!3DCC! \left( { - \infty ;\, - 1} \right)\) và \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaeWaaeaacq % GHsislcaaIXaGaai4oaiaaykW7cqGHRaWkcqGHEisPaiaawIcacaGL % Paaaaaa!3DC1! \left( { - 1;\, + \infty } \right)\).

Xét hàm số: \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9maalaaabaGaaGOmaiaadIhacqGHRaWkcaaIXaaabaGaamiEaiab % gUcaRiaaigdaaaaaaa!3DF8! y = \frac{{2x + 1}}{{x + 1}}\)

Tập xác định: \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiraiabg2 % da9iabl2riHkaacYfadaGadaqaaiabgkHiTiaaigdaaiaawUhacaGL % 9baaaaa!3DEB! [D = R\backslash \left\{ { - 1} \right\}\)

\(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGabmyEayaafa % Gaeyypa0ZaaSaaaeaacaaIXaaabaWaaeWaaeaacaWG4bGaey4kaSIa % aGymaaGaayjkaiaawMcaamaaCaaaleqabaGaaGOmaaaaaaGccqGH+a % GpcaaIWaGaaiilaiaaykW7cqGHaiIicaWG4bGaeyicI4Saamiraaaa % !45FB! y' = \frac{1}{{{{\left( {x + 1} \right)}^2}}} > 0,\,\forall x \in D\)

Hàm số đồng biến trên mỗi khoảng \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaeWaaeaacq % GHsislcqGHEisPcaGG7aGaaGPaVlabgkHiTiaaigdaaiaawIcacaGL % Paaaaaa!3DCC! \left( { - \infty ;\, - 1} \right)\) và \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaeWaaeaacq % GHsislcaaIXaGaai4oaiaaykW7cqGHRaWkcqGHEisPaiaawIcacaGL % Paaaaaa!3DC1! \left( { - 1;\, + \infty } \right)\)

Tiệm cận đứng là đường thẳng ​\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiEaiabg2 % da9iabgkHiTiaaigdaaaa!399F! x = - 1\)

Tiệm cận ngang là đường thẳng \(y=2\)

\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyDamaaBa % aaleaacaaI4aaabeaakiabg2da9iaadwhadaWgaaWcbaGaaGymaaqa % baGccqGHRaWkcaaI3aGaamizaaaa!3D63! {u_8} = {u_1} + 7d\)\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyi1HSTaaG % OmaiaaiAdacaaMc8Uaeyypa0ZaaSaaaeaacaaIXaaabaGaaG4maaaa % cqGHRaWkcaaI3aGaamizaaaa!4071! \Leftrightarrow 26\, = \frac{1}{3} + 7d\)\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyDamaaBa % aaleaacaaI4aaabeaakiabg2da9iaadwhadaWgaaWcbaGaaGymaaqa % baGccqGHRaWkcaaI3aGaamizaaaa!3D63! {u_8} = {u_1} + 7d\)\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyi1HSTaaG % OmaiaaiAdacaaMc8Uaeyypa0ZaaSaaaeaacaaIXaaabaGaaG4maaaa % cqGHRaWkcaaI3aGaamizaaaa!4071! \Leftrightarrow 26\, = \frac{1}{3} + 7d\)\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyi1HSTaam % izaiabg2da9maalaaabaGaaGymaiaaigdaaeaacaaIZaaaaaaa!3C82! \Leftrightarrow d = \frac{{11}}{3}\)

TXĐ: \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiraiabg2 % da9iabl2riHkaacYfadaGadaqaaiabgkHiTiaaigdacaGG7aWaaSaa % aeaacaaIZaaabaGaaGynaaaaaiaawUhacaGL9baaaaa!4037! D = R\backslash \left\{ { - 1;\frac{3}{5}} \right\}\)

Ta có: \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaCbeaeaaci % GGSbGaaiyAaiaac2gaaSqaaiaadIhacqGHsgIRcqGHRaWkcqGHEisP % aeqaaOWaaSaaaeaacaWG4bWaaWbaaSqabeaacaaIYaaaaOGaey4kaS % IaamiEaiabgUcaRiaaigdaaeaacqGHsislcaaI1aGaamiEamaaCaaa % leqabaGaaGOmaaaakiabgkHiTiaaikdacaWG4bGaey4kaSIaaG4maa % aacqGH9aqpcqGHsisldaWcaaqaaiaaigdaaeaacaaI1aaaaaaa!4F1E! \mathop {\lim }\limits_{x \to + \infty } \frac{{{x^2} + x + 1}}{{ - 5{x^2} - 2x + 3}} = - \frac{1}{5}\); \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaCbeaeaaci % GGSbGaaiyAaiaac2gaaSqaaiaadIhacqGHsgIRcqGHsislcqGHEisP % aeqaaOWaaSaaaeaacaWG4bWaaWbaaSqabeaacaaIYaaaaOGaey4kaS % IaamiEaiabgUcaRiaaigdaaeaacqGHsislcaaI1aGaamiEamaaCaaa % leqabaGaaGOmaaaakiabgkHiTiaaikdacaWG4bGaey4kaSIaaG4maa % aacqGH9aqpcqGHsisldaWcaaqaaiaaigdaaeaacaaI1aaaaaaa!4F29! \mathop {\lim }\limits_{x \to - \infty } \frac{{{x^2} + x + 1}}{{ - 5{x^2} - 2x + 3}} = - \frac{1}{5}\)\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaCbeaeaaci % GGSbGaaiyAaiaac2gaaSqaaiaadIhacqGHsgIRcqGHsislcqGHEisP % aeqaaOWaaSaaaeaacaWG4bWaaWbaaSqabeaacaaIYaaaaOGaey4kaS % IaamiEaiabgUcaRiaaigdaaeaacqGHsislcaaI1aGaamiEamaaCaaa % leqabaGaaGOmaaaakiabgkHiTiaaikdacaWG4bGaey4kaSIaaG4maa % aacqGH9aqpcqGHsisldaWcaaqaaiaaigdaaeaacaaI1aaaaaaa!4F29! \mathop {\lim }\limits_{x \to - \infty } \frac{{{x^2} + x + 1}}{{ - 5{x^2} - 2x + 3}} = - \frac{1}{5}\)\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyO0H4naaa!3851! \Rightarrow \) đường thẳng \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9iabgkHiTmaalaaabaGaaGymaaqaaiaaiwdaaaaaaa!3A6F! y = - \frac{1}{5}\) \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9iabgkHiTmaalaaabaGaaGymaaqaaiaaiwdaaaaaaa!3A6F! y = - \frac{1}{5}\)là đường tiệm cận ngang của đồ thị hàm số.

\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaCbeaeaaci % GGSbGaaiyAaiaac2gaaSqaaiaadIhacqGHsgIRcqGHsislcaaIXaWa % aWbaaWqabeaacqGHRaWkaaaaleqaaOWaaSaaaeaacaWG4bWaaWbaaS % qabeaacaaIYaaaaOGaey4kaSIaamiEaiabgUcaRiaaigdaaeaacqGH % sislcaaI1aGaamiEamaaCaaaleqabaGaaGOmaaaakiabgkHiTiaaik % dacaWG4bGaey4kaSIaaG4maaaacqGH9aqpcqGHRaWkcqGHEisPaaa!4F6A! \mathop {\lim }\limits_{x \to - {1^ + }} \frac{{{x^2} + x + 1}}{{ - 5{x^2} - 2x + 3}} = + \infty \)\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaCbeaeaaci % GGSbGaaiyAaiaac2gaaSqaaiaadIhacqGHsgIRcqGHsislcaaIXaWa % aWbaaWqabeaacqGHRaWkaaaaleqaaOWaaSaaaeaacaWG4bWaaWbaaS % qabeaacaaIYaaaaOGaey4kaSIaamiEaiabgUcaRiaaigdaaeaacqGH % sislcaaI1aGaamiEamaaCaaaleqabaGaaGOmaaaakiabgkHiTiaaik % dacaWG4bGaey4kaSIaaG4maaaacqGH9aqpcqGHRaWkcqGHEisPaaa!4F6A! \mathop {\lim }\limits_{x \to - {1^ + }} \frac{{{x^2} + x + 1}}{{ - 5{x^2} - 2x + 3}} = + \infty \)  \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyO0H4naaa!3851! \Rightarrow \)đường thẳng \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiEaiabg2 % da9iabgkHiTiaaigdaaaa!399F! x= - 1\)\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiEaiabg2 % da9iabgkHiTiaaigdaaaa!399F! x = - 1\) là đường tiệm cận đứng của đồ thị hàm số.

\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaCbeaeaaci % GGSbGaaiyAaiaac2gaaSqaaiaadIhacqGHsgIRdaWcaaqaaiaaioda % aeaacaaI1aaaamaaCaaameqabaGaey4kaScaaaWcbeaakmaalaaaba % GaamiEamaaCaaaleqabaGaaGOmaaaakiabgUcaRiaadIhacqGHRaWk % caaIXaaabaGaeyOeI0IaaGynaiaadIhadaahaaWcbeqaaiaaikdaaa % GccqGHsislcaaIYaGaamiEaiabgUcaRiaaiodaaaGaeyypa0JaeyOe % I0IaeyOhIukaaa!4F59! \mathop {\lim }\limits_{x \to {{\frac{3}{5}}^ + }} \frac{{{x^2} + x + 1}}{{ - 5{x^2} - 2x + 3}} = - \infty \)\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyO0H4naaa!3851! \Rightarrow \)\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaCbeaeaaci % GGSbGaaiyAaiaac2gaaSqaaiaadIhacqGHsgIRdaWcaaqaaiaaioda % aeaacaaI1aaaamaaCaaameqabaGaey4kaScaaaWcbeaakmaalaaaba % GaamiEamaaCaaaleqabaGaaGOmaaaakiabgUcaRiaadIhacqGHRaWk % caaIXaaabaGaeyOeI0IaaGynaiaadIhadaahaaWcbeqaaiaaikdaaa % GccqGHsislcaaIYaGaamiEaiabgUcaRiaaiodaaaGaeyypa0JaeyOe % I0IaeyOhIukaaa!4F59! \mathop {\lim }\limits_{x \to {{\frac{3}{5}}^ + }} \frac{{{x^2} + x + 1}}{{ - 5{x^2} - 2x + 3}} = - \infty \) \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyO0H4naaa!3851! \Rightarrow \) đường thẳng \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiEaiabg2 % da9maalaaabaGaaG4maaqaaiaaiwdaaaaaaa!3983! x = \frac{3}{5}\) là đường tiệm cận đứng của đồ thị hàm số.

Vậy đồ thị của hàm số đã cho có \(3\) đường tiệm cận.

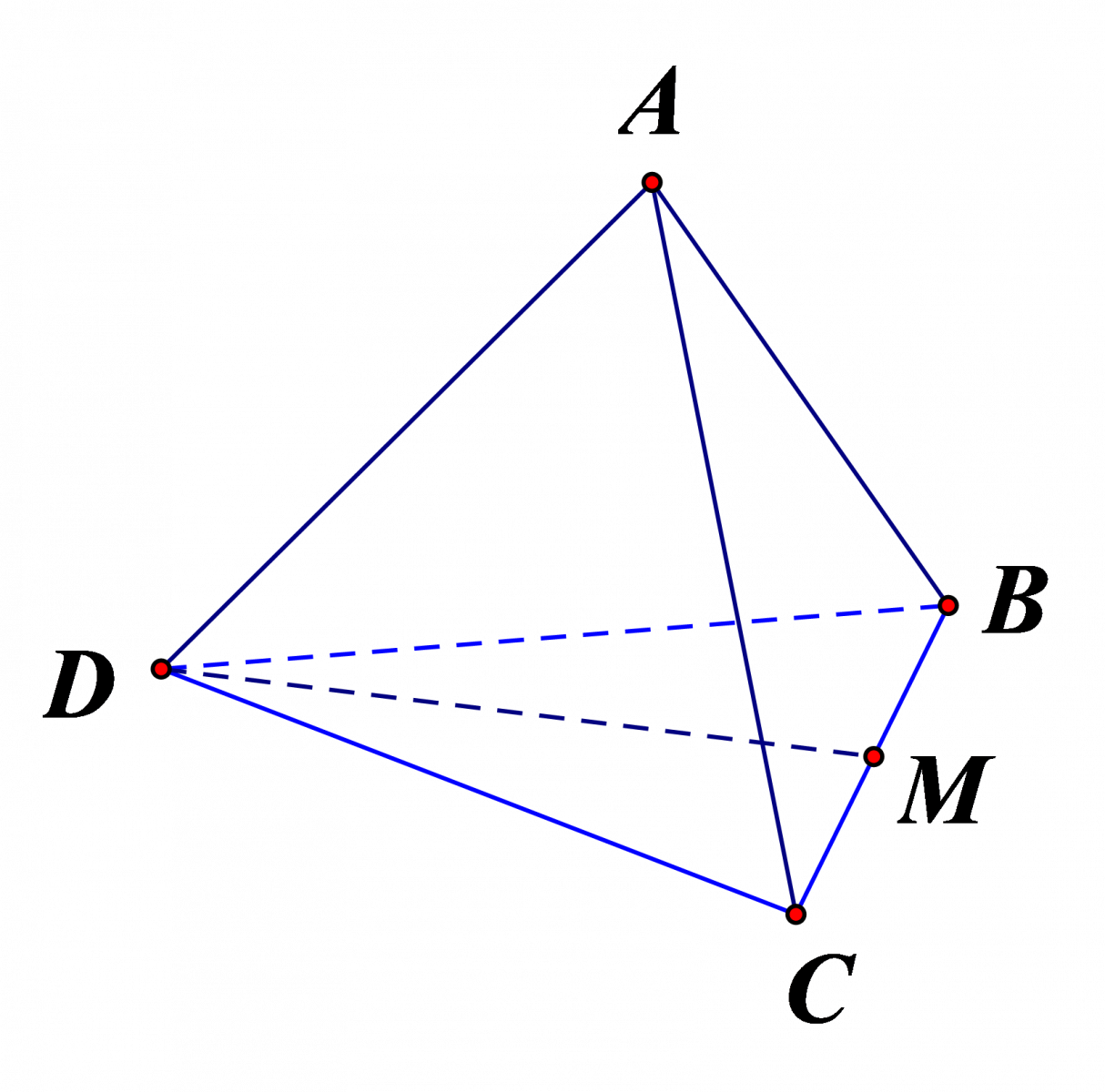
Giả sử tứ diện đều \(ABCD\) có cạnh bằng \(a\) ta có: \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiraiaad2 % eacqGH9aqpdaWcaaqaaiaadggadaGcaaqaaiaaiodaaSqabaaakeaa % caaIYaaaaaaa!3B29! DM = \frac{{a\sqrt 3 }}{2}\).

Ta lại có: \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaci4yaiaac+ % gacaGGZbWaaeWaaeaadaWhcaqaaiaadgeacaWGcbaacaGLxdcacaGG % SaWaa8HaaeaacaWGebGaamytaaGaay51GaaacaGLOaGaayzkaaGaey % ypa0ZaaSaaaeaadaWhcaqaaiaadgeacaWGcbaacaGLxdcacaGGUaWa % a8HaaeaacaWGebGaamytaaGaay51GaaabaWaaqWaaeaadaWhcaqaai % aadgeacaWGcbaacaGLxdcaaiaawEa7caGLiWoacaGGUaWaaqWaaeaa % daWhcaqaaiaadseacaWGnbaacaGLxdcaaiaawEa7caGLiWoaaaaaaa!576E! \cos \left( {\overrightarrow {AB} ,\overrightarrow {DM} } \right) = \frac{{\overrightarrow {AB} .\overrightarrow {DM} }}{{\left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {DM} } \right|}}\)  \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyypa0ZaaS % aaaeaadaWhcaqaaiaadgeacaWGcbaacaGLxdcacaGGUaWaa8Haaeaa % caWGebGaamOqaaGaay51GaGaey4kaSYaa8HaaeaacaWGbbGaamOqaa % Gaay51GaGaaiOlamaaFiaabaGaamOqaiaad2eaaiaawEniaaqaaiaa % dggacaGGUaWaaSaaaeaacaWGHbWaaOaaaeaacaaIZaaaleqaaaGcba % GaaGOmaaaaaaaaaa!4A8F! = \frac{{\overrightarrow {AB} .\overrightarrow {DB} + \overrightarrow {AB} .\overrightarrow {BM} }}{{a.\frac{{a\sqrt 3 }}{2}}}\)

  .\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyypa0ZaaS % aaaeaacaWGHbGaaiOlaiaadggacaGGUaGaci4yaiaac+gacaGGZbGa % aGOnaiaaicdacqGHWcaScqGHRaWkcaWGHbGaaiOlamaalaaabaGaam % yyaaqaaiaaikdaaaGaaiOlaiGacogacaGGVbGaai4CaiaaigdacaaI % YaGaaGimaiabgclaWcqaaiaadggacaGGUaWaaSaaaeaacaWGHbWaaO % aaaeaacaaIZaaaleqaaaGcbaGaaGOmaaaaaaaaaa!506D! = \frac{{a.a.\cos 60^\circ + a.\frac{a}{2}.\cos 120^\circ }}{{a.\frac{{a\sqrt 3 }}{2}}}\)\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyypa0ZaaS % aaaeaadaWcaaqaaiaadggadaahaaWcbeqaaiaaikdaaaaakeaacaaI % 0aaaaaqaaiaadggacaGGUaWaaSaaaeaacaWGHbWaaOaaaeaacaaIZa % aaleqaaaGcbaGaaGOmaaaaaaGaeyypa0ZaaSaaaeaadaGcaaqaaiaa % iodaaSqabaaakeaacaaI2aaaaaaa!4095! = \frac{{\frac{{{a^2}}}{4}}}{{a.\frac{{a\sqrt 3 }}{2}}} = \frac{{\sqrt 3 }}{6}\)

Vậy \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaci4yaiaac+ % gacaGGZbWaaeWaaeaacaWGbbGaamOqaiaacYcacaWGebGaamytaaGa % ayjkaiaawMcaaiabg2da9maalaaabaWaaOaaaeaacaaIZaaaleqaaa % GcbaGaaGOnaaaaaaa!40E0! \cos \left( {AB,DM} \right) = \frac{{\sqrt 3 }}{6}\)

Do hàm số đồng biến trên \(R\) nên loại ý C; D vì hai hàm số này không có tập xác định là \(R\).

Loại ý A vì đây là hàm trùng phương.

Vậy chọn ý B.

Ta có: \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiAaiabg2 % da9iaadofacaWGbbGaeyypa0JaamyyamaakaaabaGaaG4maaWcbeaa % aaa!3C49! h = SA = a\sqrt 3 \) ; \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOqaiabg2 % da9iaadofadaWgaaWcbaGaamyqaiaadkeacaWGdbGaamiraaqabaGc % cqGH9aqpcaWGHbWaaWbaaSqabeaacaaIYaaaaaaa!3EC2! B = {S_{ABCD}} = {a^2}\).

           \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOvaiabg2 % da9maalaaabaGaaGymaaqaaiaaiodaaaGaamOqaiaac6cacaWGObGa % eyypa0ZaaSaaaeaacaWGHbWaaWbaaSqabeaacaaIZaaaaOWaaOaaae % aacaaIZaaaleqaaaGcbaGaaG4maaaaaaa!4052! V = \frac{1}{3}B.h = \frac{{{a^3}\sqrt 3 }}{3}\)

Ta có: \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaCbeaeaaci % GGSbGaaiyAaiaac2gaaSqaaiaadIhacqGHsgIRcqGHRaWkcqGHEisP % aeqaaOWaaSaaaeaacaaIXaGaey4kaSIaaG4maiaadIhaaeaadaGcaa % qaaiaaikdacaWG4bWaaWbaaSqabeaacaaIYaaaaOGaey4kaSIaaG4m % aaWcbeaaaaGccqGH9aqpdaWfqaqaaiGacYgacaGGPbGaaiyBaaWcba % GaamiEaiabgkziUkabgUcaRiabg6HiLcqabaGcdaWcaaqaaiaadIha % daqadaqaamaalaaabaGaaGymaaqaaiaadIhaaaGaey4kaSIaaG4maa % GaayjkaiaawMcaaaqaamaaemaabaGaamiEaaGaay5bSlaawIa7amaa % kaaabaGaaGOmaiabgUcaRmaalaaabaGaaG4maaqaaiaadIhadaahaa % WcbeqaaiaaikdaaaaaaaqabaaaaOGaeyypa0ZaaCbeaeaaciGGSbGa % aiyAaiaac2gaaSqaaiaadIhacqGHsgIRcqGHRaWkcqGHEisPaeqaaO % WaaSaaaeaadaWcaaqaaiaaigdaaeaacaWG4baaaiabgUcaRiaaioda % aeaadaGcaaqaaiaaikdacqGHRaWkdaWcaaqaaiaaiodaaeaacaWG4b % WaaWbaaSqabeaacaaIYaaaaaaaaeqaaaaaaaa!6F26! \mathop {\lim }\limits_{x \to + \infty } \frac{{1 + 3x}}{{\sqrt {2{x^2} + 3} }} = \mathop {\lim }\limits_{x \to + \infty } \frac{{x\left( {\frac{1}{x} + 3} \right)}}{{\left| x \right|\sqrt {2 + \frac{3}{{{x^2}}}} }} = \mathop {\lim }\limits_{x \to + \infty } \frac{{\frac{1}{x} + 3}}{{\sqrt {2 + \frac{3}{{{x^2}}}} }}\)\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyypa0ZaaS % aaaeaacaaIZaaabaWaaOaaaeaacaaIYaaaleqaaaaakiabg2da9maa % laaabaGaaG4mamaakaaabaGaaGOmaaWcbeaaaOqaaiaaikdaaaaaaa!3C18! = \frac{3}{{\sqrt 2 }} = \frac{{3\sqrt 2 }}{2}\)

Lấy điểm M trên a , qua M kẻ đường thẳng b' song song với b . Khi đó mặt phẳng (a;b') song song với b .

Nếu có một mặt phẳng (P) khác (a;b') qua a mà song song với P khi đó \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaeWaaeaaca % WGqbaacaGLOaGaayzkaaGaeyykIC8aaeWaaeaacaWGHbGaai4oaiaa % ykW7ceWGIbGbauaaaiaawIcacaGLPaaacqGH9aqpcaWGHbaaaa!4188! \left( P \right) \cap \left( {a;\,b'} \right) = a\) phải song song với b . Mâu thuẩn a,b  chéo nhau. Vậy có duy nhất một mặt phẳng chứa a và song song với b.

Gọi h là khoảng cách từ \(C'\) đến mặt phẳng \((ABC)\) và \(B\) là diện tích tam giác \(ABC\). Khi đó, thể tích lăng trụ \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOvaiabg2 % da9iaadkeacaWGObaaaa!3989! V = Bh\), thể tích khối chóp \(C'.ABC\) là  \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOvamaaBa % aaleaaceWGdbGbauaacaGGUaGaamyqaiaadkeacaWGdbaabeaakiab % g2da9maalaaabaGaaGymaaqaaiaaiodaaaGaamOqaiaadIgaaaa!3F21! {V_{C'.ABC}} = \frac{1}{3}Bh\). Do đó, \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOvamaaBa % aaleaaceWGdbGbauaacaGGUaGaamyqaiaadkeacaWGdbaabeaakiab % g2da9maalaaabaGaaGymaaqaaiaaiodaaaGaamOvaaaa!3E48! {V_{C'.ABC}} = \frac{1}{3}V\).

Công thức tính số tổ hợp là \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4qamaaDa % aaleaacaWGUbaabaGaam4Aaaaakiabg2da9maalaaabaGaamOBaiaa % cgcaaeaadaqadaqaaiaad6gacqGHsislcaWGRbaacaGLOaGaayzkaa % GaaiyiaiaadUgacaGGHaaaaaaa!4216! C_n^k = \frac{{n!}}{{\left( {n - k} \right)!k!}}\)

Gọi E là trung điểm của BC . Tam giác ABC cân nên \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOqaiaado % eacqGHLkIxcaWGbbGaamyraaaa!3AC4! BC \bot AE\);

Tam giác DBC cân nên \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOqaiaado % eacqGHLkIxcaWGebGaamyraaaa!3AC7! BC \bot DE\) . Do đó \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOqaiaado % eacqGHLkIxdaqadaqaaiaadgeacaWGfbGaamiraaGaayjkaiaawMca % aiabgkDiElaadkeacaWGdbGaeyyPI4Laamyqaiaadseaaaa!4442! BC \bot \left( {AED} \right) \Rightarrow BC \bot AD\).

Hình lập phương có 9 mặt phẳng đối xứng.

Công thức tính thể tích khối lăng trụ là: \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOvaiabg2 % da9iaadkeacaGGUaGaamiAaaaa!3A3B! V = B.h\) .

Hàm số \(f(x)\) xác định trên nửa khoảng \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaKGeaeaacq % GHsislcaaIYaGaai4oaiabgUcaRiabg6HiLcGaay5waiaawMcaaaaa % !3C81! \left[ { - 2; + \infty } \right)\).  

Ta có: \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaCbeaeaaci % GGSbGaaiyAaiaac2gaaSqaaiaadIhacqGHsgIRdaqadaqaaiabgkHi % TiaaikdaaiaawIcacaGLPaaadaahaaadbeqaaiabgUcaRaaaaSqaba % GccaWGMbWaaeWaaeaacaWG4baacaGLOaGaayzkaaGaeyypa0ZaaCbe % aeaaciGGSbGaaiyAaiaac2gaaSqaaiaadIhacqGHsgIRdaqadaqaai % abgkHiTiaaikdaaiaawIcacaGLPaaadaahaaadbeqaaiabgUcaRaaa % aSqabaGcdaWcaaqaamaakaaabaGaaGOmaiaadIhacqGHRaWkcaaI4a % aaleqaaOGaeyOeI0IaaGOmaaqaamaakaaabaGaamiEaiabgUcaRiaa % ikdaaSqabaaaaaaa!56EF! \mathop {\lim }\limits_{x \to {{\left( { - 2} \right)}^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {{\left( { - 2} \right)}^ + }} \frac{{\sqrt {2x + 8} - 2}}{{\sqrt {x + 2} }}\)\(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyypa0ZaaC % beaeaaciGGSbGaaiyAaiaac2gaaSqaaiaadIhacqGHsgIRdaqadaqa % aiabgkHiTiaaikdaaiaawIcacaGLPaaadaahaaadbeqaaiabgUcaRa % aaaSqabaGcdaWcaaqaaiaaikdacaWG4bGaey4kaSIaaGioaiabgkHi % TiaaisdaaeaadaGcaaqaaiaadIhacqGHRaWkcaaIYaaaleqaaOWaae % WaaeaadaGcaaqaaiaaikdacaWG4bGaey4kaSIaaGioaaWcbeaakiab % gUcaRiaaisdaaiaawIcacaGLPaaaaaaaaa!4FC6! = \mathop {\lim }\limits_{x \to {{\left( { - 2} \right)}^ + }} \frac{{2x + 8 - 4}}{{\sqrt {x + 2} \left( {\sqrt {2x + 8} + 4} \right)}}\) \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyypa0ZaaC % beaeaaciGGSbGaaiyAaiaac2gaaSqaaiaadIhacqGHsgIRdaqadaqa % aiabgkHiTiaaikdaaiaawIcacaGLPaaadaahaaadbeqaaiabgUcaRa % aaaSqabaGcdaWcaaqaaiaaikdadaGcaaqaaiaadIhacqGHRaWkcaaI % YaaaleqaaaGcbaWaaOaaaeaacaaIYaGaamiEaiabgUcaRiaaiIdaaS % qabaGccqGHRaWkcaaI0aaaaiabg2da9iaaicdaaaa!4BB1! = \mathop {\lim }\limits_{x \to {{\left( { - 2} \right)}^ + }} \frac{{2\sqrt {x + 2} }}{{\sqrt {2x + 8} + 4}} = 0\)

Khẳng định (I) đúng.

Ta có \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaCbeaeaaci % GGSbGaaiyAaiaac2gaaSqaaiaadIhacqGHsgIRdaqadaqaaiabgkHi % TiaaikdaaiaawIcacaGLPaaadaahaaadbeqaaiabgUcaRaaaaSqaba % GccaWGMbWaaeWaaeaacaWG4baacaGLOaGaayzkaaGaeyypa0ZaaCbe % aeaaciGGSbGaaiyAaiaac2gaaSqaaiaadIhacqGHsgIRdaqadaqaai % abgkHiTiaaikdaaiaawIcacaGLPaaadaahaaadbeqaaiabgkHiTaaa % aSqabaGccaWGMbWaaeWaaeaacaWG4baacaGLOaGaayzkaaGaeyypa0 % JaamOzamaabmaabaGaeyOeI0IaaGOmaaGaayjkaiaawMcaaiabg2da % 9iaaicdaaaa!595D! \mathop {\lim }\limits_{x \to {{\left( { - 2} \right)}^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {{\left( { - 2} \right)}^ - }} f\left( x \right) = f\left( { - 2} \right) = 0\) , theo định nghĩa hàm số liên tục trên một đoạn thì hàm số liên tục tại x = -2 . Khẳng định (II) đúng, khẳng định (III) sai.

Xét hình lập phương ABCD.A'B'C'D'.

Mặt phẳng (ABCD) và (A'B'C'D') lần lượt chứa hai đường thẳng song song là AB và A'B' nhưng hai mặt phẳng này không song song với nhau. Đáp án A sai.

Hai mặt phẳng (ABCD) và (A'B'C'D') song song với nhau nhưng hai đường thẳng CD và A'D' lần lượt nằm trên hai mặt phẳng này không song song với nhau. Đáp án B sai.

Hai mặt phẳng chỉ có ba vị trí tương đối: song song, cắt nhau, trùng nhau. Nếu hai mặt phẳng phân biệt không song song thì chúng phải cắt nhau. Đáp án C đúng.

Hai mặt phẳng (ADA'D') và (CDC'D') cùng song song với đường thẳng BB' nhưng chúng không song song với nhau. Đáp án D sai.

Theo công thức tỉ số thể tích khối chóp, ta được: \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaace % WGwbGbauaaaeaacaWGwbaaaiabg2da9maalaaabaGaam4uaiqadgea % gaqbaaqaaiaadofacaWGbbaaaiaac6cadaWcaaqaaiaadofaceWGcb % GbauaaaeaacaWGtbGaamOqaaaacaGGUaWaaSaaaeaacaWGtbGabm4q % ayaafaaabaGaam4uaiaadoeaaaGaeyypa0ZaaSaaaeaacaaIXaaaba % GaaGOmaaaacaGGUaWaaSaaaeaacaaIXaaabaGaaG4maaaacaGGUaWa % aSaaaeaacaaIXaaabaGaaGinaaaacqGH9aqpdaWcaaqaaiaaigdaae % aacaaIYaGaaGinaaaaaaa!4E8A! \frac{{V'}}{V} = \frac{{SA'}}{{SA}}.\frac{{SB'}}{{SB}}.\frac{{SC'}}{{SC}} = \frac{1}{2}.\frac{1}{3}.\frac{1}{4} = \frac{1}{{24}}\).

[phương pháp tự luận]

Điều kiện: \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOBaiabgw % MiZkaaiodaaaa!3969! n \ge 3\) , \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbiqaaqugcaWGUb % GaeyicI4SaeSyfHukaaa!3A37! n \in N\) .

\(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyqamaaDa % aaleaacaWGUbaabaGaaG4maaaakiabg2da9iaaikdacaaIWaGaamOB % aiabgsDiBpaalaaabaGaamOBaiaacgcaaeaadaqadaqaaiaad6gacq % GHsislcaaIZaaacaGLOaGaayzkaaGaaiyiaaaacqGH9aqpcaaIYaGa % aGimaiaad6gaaaa!484D! A_n^3 = 20n \Leftrightarrow \frac{{n!}}{{\left( {n - 3} \right)!}} = 20n\)\(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyi1HS9aae % WaaeaacaWGUbGaeyOeI0IaaGOmaaGaayjkaiaawMcaamaabmaabaGa % amOBaiabgkHiTiaaigdaaiaawIcacaGLPaaacaWGUbGaeyypa0JaaG % OmaiaaicdacaWGUbaaaa!44FA! \Leftrightarrow \left( {n - 2} \right)\left( {n - 1} \right)n = 20n\)\(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyi1HSTaam % OBamaabmaabaGaamOBamaaCaaaleqabaGaaGOmaaaakiabgkHiTiaa % iodacaWGUbGaeyOeI0IaaGymaiaaiIdaaiaawIcacaGLPaaacqGH9a % qpcaaIWaaaaa!4378! \Leftrightarrow n\left( {{n^2} - 3n - 18} \right) = 0\)\(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyi1HS9aam % qaaqaabeqaaiaad6gacqGH9aqpcaaI2aaabaGaamOBaiabg2da9iab % gkHiTiaaiodaaeaacaWGUbGaeyypa0JaaGimaaaacaGLBbaaaaa!4261! \Leftrightarrow \left[ \begin{array}{l} n = 6\\ n = - 3\\ n = 0 \end{array} \right.\)

Kết hợp điều kiện, ta được \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOBaiabg2 % da9iaaiAdaaaa!38AC! n = 6\).

[phương pháp trắc nghiệm]

Nhập vào máy tính vế trái trừ đi vế phải:

CALC lần lượt các đáp án, ta được đáp án A thỏa mãn vế trái trừ vế phải bằng 0.

\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGabmyEayaafa % Gaeyypa0JaaGOmaiGacogacaGGVbGaai4CaiaaikdacaWG4baaaa!3D4C! y' = 2\cos 2x\)\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyO0H4Tabm % yEayaafyaafaGaeyypa0JaeyOeI0IaaGinaiGacohacaGGPbGaaiOB % aiaaikdacaWG4baaaa!40A8! \Rightarrow y'' = - 4\sin 2x\)

\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEamaaCa % aaleqabaGaaGOmaaaakiabgkHiTmaabmaabaGabmyEayaafaaacaGL % OaGaayzkaaWaaWbaaSqabeaacaaIYaaaaOGaeyypa0Jaci4CaiaacM % gacaGGUbWaaWbaaSqabeaacaaIYaaaaOGaaGOmaiaadIhacqGHsisl % caaI0aGaci4yaiaac+gacaGGZbWaaWbaaSqabeaacaaIYaaaaOGaaG % OmaiaadIhacqGHGjsUcaaI0aaaaa!4C91! {y^2} - {\left( {y'} \right)^2} = {\sin ^2}2x - 4{\cos ^2}2x \ne 4\)\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyO0H4naaa!3851! \Rightarrow \) A sai

\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaaGinaiaadM % hacqGHRaWkceWG5bGbauGbauaacqGH9aqpcaaI0aGaci4CaiaacMga % caGGUbGaaGOmaiaadIhacqGHsislcaaI0aGaci4CaiaacMgacaGGUb % GaaGOmaiaadIhacqGH9aqpcaaIWaaaaa!47F8! 4y + y'' = 4\sin 2x - 4\sin 2x = 0\)\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyO0H4naaa!3851! \Rightarrow \) B đúng

Tương tự ta kiểm tra được C, D sai.

\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOzamaabm % aabaGaamiEaaGaayjkaiaawMcaaiabg2da9maalaaabaGaamiEamaa % CaaaleqabaGaaGOmaaaakiabgUcaRiaadIhacqGHRaWkcaaIXaaaba % GaamiEaiabgUcaRiaaigdaaaaaaa!4281! f\left( x \right) = \frac{{{x^2} + x + 1}}{{x + 1}}\) TXĐ \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiraiabg2 % da9iabl2riHkaacYfadaGadaqaaiabgkHiTiaaigdaaiaawUhacaGL % 9baaaaa!3DEC! D = R\backslash \left\{ { - 1} \right\}\)

\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGabmOzayaafa % WaaeWaaeaacaWG4baacaGLOaGaayzkaaGaeyypa0ZaaSaaaeaacaWG % 4bWaaWbaaSqabeaacaaIYaaaaOGaey4kaSIaaGOmaiaadIhaaeaada % qadaqaaiaadIhacqGHRaWkcaaIXaaacaGLOaGaayzkaaWaaWbaaSqa % beaacaaIYaaaaaaakiabg2da9iaaicdaaaa!45E8! f'\left( x \right) = \frac{{{x^2} + 2x}}{{{{\left( {x + 1} \right)}^2}}} = 0\)\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyi1HS9aam % qaaqaabeqaaiaadIhacqGH9aqpcaaIWaaabaGaamiEaiabg2da9iab % gkHiTiaaikdaaaGaay5waaaaaa!3FBB! \Leftrightarrow \left[ \begin{array}{l} x = 0\\ x = - 2 \end{array} \right.\)

\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaCbeaeaaci % GGSbGaaiyAaiaac2gaaSqaaiaadIhacqGHsgIRcqGHXcqScqGHEisP % aeqaaOGaamyEaiabg2da9iabgglaXkabg6HiLcaa!44B3! \mathop {\lim }\limits_{x \to \pm \infty } y = \pm \infty \) và \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaCbeaeaaci % GGSbGaaiyAaiaac2gaaSqaaiaadIhacqGHsgIRcqGHsislcaaIXaWa % aWbaaWqabeaacqGHsislaaaaleqaaOGaamyEaiabg2da9iabgkHiTi % abg6HiLcaa!4321! \mathop {\lim }\limits_{x \to - {1^ - }} y = - \infty \); \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaCbeaeaaci % GGSbGaaiyAaiaac2gaaSqaaiaadIhacqGHsgIRcqGHsislcaaIXaWa % aWbaaWqabeaacqGHRaWkaaaaleqaaOGaamyEaiabg2da9iabgUcaRi % abg6HiLcaa!430B! \mathop {\lim }\limits_{x \to - {1^ + }} y = + \infty \)

Bảng biến thiên:

Từ bảng biến thiên suy ra hàm số có 2 điểm cực trị.

Dựa vào đồ thị ta suy ra hàm số có dạng: \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 %da9iaadggacaWG4bWaaWbaaSqabeaacaaI0aaaaOGaey4kaSIaamOy % aiaadIhadaahaaWcbeqaaiaaikdaaaGccqGHRaWkcaWGJbaaaa!4053! y = a{x^4} + b{x^2} + c\)  với  \(a < 0\)

 \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyO0H4naaa!3851! \Rightarrow \)Loại đáp án D.

Đáp án B loại vì: \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGabmyEayaafa % Gaeyypa0JaeyOeI0IaaGinaiaadIhadaahaaWcbeqaaiaaiodaaaGc % cqGHsislcaaI0aGaamiEaiabg2da9iaaicdaaaa!4008! y' = - 4{x^3} - 4x = 0\)  \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyi1HSTaam % iEaiabg2da9iaaicdaaaa!3B0D! \Leftrightarrow x = 0\)  \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyO0H4naaa!3851! \Rightarrow \)  Đồ thị hàm số có 1 điểm cực trị.

Đáp án A: \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGabmyEayaafa % Gaeyypa0JaeyOeI0IaaGinaiaadIhadaahaaWcbeqaaiaaiodaaaGc % cqGHRaWkcaaI4aGaamiEaiabg2da9iaaicdaaaa!4001! y' = - 4{x^3} + 8x = 0\) \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyi1HS9aam % qaaqaabeqaaiaadIhacqGH9aqpcaaIWaaabaGaamiEaiabg2da9iab % gglaXoaakaaabaGaaGOmaaWcbeaaaaGccaGLBbaaaaa!40E1! \Leftrightarrow \left[ \begin{array}{l} x = 0\\ x = \pm \sqrt 2 \end{array} \right.\) \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyO0H4naaa!3851! \Rightarrow \) Đồ thị hàm số có 3 điểm cực trị lần lượt là: O(0;0) , \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyqamaabm % aabaWaaOaaaeaacaaIYaaaleqaaOGaai4oaiaaisdaaiaawIcacaGL % Paaaaaa!3AA1! A\left( {\sqrt 2 ;4} \right)\), \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOqamaabm % aabaGaeyOeI0YaaOaaaeaacaaIYaaaleqaaOGaai4oaiaaisdaaiaa % wIcacaGLPaaaaaa!3B8F! B\left( { - \sqrt 2 ;4} \right)\).

Vậy chọn đáp án A.

Gọi M là trung điểm của AC \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyO0H4Taam % Oqaiaad2eacqGH9aqpcaWGbbGaamytaiabg2da9iaadoeacaWGnbGa % eyypa0ZaaSaaaeaacaaIXaaabaGaaGOmaaaacaWGbbGaam4qaaaa!4343! \Rightarrow BM = AM = CM = \frac{1}{2}AC\).

 \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyiLdqKaam % 4uaiaadgeacaWGdbaaaa!39C1! \Delta SAC\) cân tại  S \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyO0H4Taam % 4uaiaad2eacqGHLkIxcaWGbbGaam4qaiaaykW7caaMc8UaaGPaVpaa % bmaabaGaaGymaaGaayjkaiaawMcaaaaa!441F! \Rightarrow SM \bot AC\,\,\,\left( 1 \right)\) .

\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyiLdqKaam % 4uaiaad2eacaWGbbaaaa!39CB! \Delta SMA\) vuông tại M \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyO0H4Taam % 4uaiaadgeadaahaaWcbeqaaiaaikdaaaGccqGH9aqpcaWGbbGaamyt % amaaCaaaleqabaGaaGOmaaaakiabgUcaRiaadofacaWGnbWaaWbaaS % qabeaacaaIYaaaaaaa!41E8! \Rightarrow S{A^2} = A{M^2} + S{M^2}\) \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyi1HSTaam % 4uaiaadkeadaahaaWcbeqaaiaaikdaaaGccqGH9aqpcaWGcbGaamyt % amaaCaaaleqabaGaaGOmaaaakiabgUcaRiaadofacaWGnbWaaWbaaS % qabeaacaaIYaaaaaaa!41E8! \Leftrightarrow S{B^2} = B{M^2} + S{M^2}\)  .

\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyO0H4naaa!3851! \Rightarrow \) \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyiLdqKaam % 4uaiaad2eacaWGcbaaaa!39CC! \Delta SMB\) vuông tại M hay \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4uaiaad2 % eacqGHLkIxcaWGcbGaamytaiaaykW7caaMc8UaaGPaVpaabmaabaGa % aGOmaaGaayjkaiaawMcaaaaa!41CE! SM \bot BM\,\,\,\left( 2 \right)\)

Từ (1) và (2)  suy ra: \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4uaiaad2 % eacqGHLkIxdaqadaqaaiaadgeacaWGcbGaam4qaaGaayjkaiaawMca % aaaa!3D2D! SM \bot \left( {ABC} \right)\).

Theo giả thiết:\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4uaiaadI % eacqGHLkIxdaqadaqaaiaadgeacaWGcbGaam4qaaGaayjkaiaawMca % aaaa!3D28! SH \bot \left( {ABC} \right)\) ,  \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamisaiabgI % GiopaabmaabaGaamyqaiaadkeacaWGdbaacaGLOaGaayzkaaaaaa!3C23! H \in \left( {ABC} \right)\) \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyO0H4Taam % isaiabggMi6kaad2eaaaa!3BB9! \Rightarrow H \equiv M\).

Vậy H trùng với trung điểm AC.

Số hạng tổng quát của khai triển: \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamivamaaBa % aaleaacaWGRbGaey4kaSIaaGymaaqabaGccqGH9aqpcaWGdbWaa0ba % aSqaaiaaiAdaaeaacaWGRbaaaOGaamiEamaaCaaaleqabaGaaGOnai % abgkHiTiaadUgaaaGccaGGUaWaaeWaaeaadaWcaaqaaiaaikdaaeaa % daGcaaqaaiaadIhaaSqabaaaaaGccaGLOaGaayzkaaWaaWbaaSqabe % aacaWGRbaaaaaa!465B! {T_{k + 1}} = C_6^k{x^{6 - k}}.{\left( {\frac{2}{{\sqrt x }}} \right)^k}\) \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyypa0Jaam % 4qamaaDaaaleaacaaI2aaabaGaam4AaaaakiaaikdadaahaaWcbeqa % aiaadUgaaaGccaGGUaGaamiEamaaCaaaleqabaGaaGOnaiabgkHiTm % aalaaabaGaaG4maaqaaiaaikdaaaGaam4Aaaaaaaa!418E! = C_6^k{2^k}.{x^{6 - \frac{3}{2}k}}\)  .

Số hạng chứa \(x^3\) ứng với \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaaGOnaiabgk % HiTmaalaaabaGaaG4maaqaaiaaikdaaaGaam4Aaiabg2da9iaaioda % aaa!3BDD! 6 - \frac{3}{2}k = 3\) \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyi1HSTaam % 4Aaiabg2da9iaaikdaaaa!3B02! \Leftrightarrow k = 2\) .

Vậy hệ số của \(x^3\) là: \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4qamaaDa % aaleaacaaI2aaabaGaaGOmaaaakiaac6cacaaIYaWaaWbaaSqabeaa % caaIYaaaaOGaeyypa0JaaGOnaiaaicdaaaa!3D50! C_6^2{.2^2} = 60\).

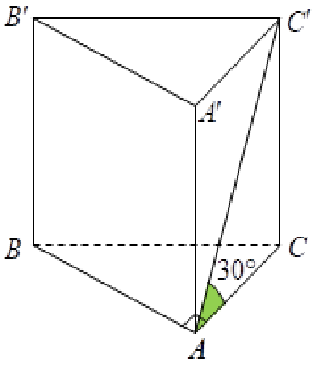
Ta có AC là hình chiếu vuông góc của AC' lên mặt phẳng (ABC) 

\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyO0H49aae % WaaeaadaqiaaqaaiaadgeaceWGdbGbauaacaGGSaGaaGPaVpaabmaa % baGaamyqaiaadkeacaWGdbaacaGLOaGaayzkaaaacaGLcmaaaiaawI % cacaGLPaaacqGH9aqpdaqiaaqaaiaadoeacaWGbbGabm4qayaafaaa % caGLcmaacqGH9aqpcaaIZaGaaGimaiabgclaWcaa!4AE2! \Rightarrow \left( {\widehat {AC',\,\left( {ABC} \right)}} \right) = \widehat {CAC'} = 30^\circ \)

Tam giác ACC' vuông tại  C có  \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4qaiqado % eagaqbaiabg2da9iaadgeacaWGdbGaaiOlaiGacshacaGGHbGaaiOB % aiaaiodacaaIWaGaeyiSaaRaeyypa0ZaaSaaaeaacaaIYaGaamyyam % aakaaabaGaaG4maaWcbeaaaOqaaiaaiodaaaaaaa!4561! CC' = AC.\tan 30^\circ = \frac{{2a\sqrt 3 }}{3}\)

Khi đó \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOvamaaBa % aaleaacaWGbbGaamOqaiaadoeacaGGUaGabmyqayaafaGabmOqayaa % faGabm4qayaafaaabeaakiabg2da9iaadofadaWgaaWcbaGaamyqai % aadkeacaWGdbaabeaakiaac6cacaWGdbGabm4qayaafaGaeyypa0Za % aSaaaeaacaaI0aGaamyyamaaCaaaleqabaGaaG4maaaakmaakaaaba % GaaG4maaWcbeaaaOqaaiaaiodaaaaaaa!4889! {V_{ABC.A'B'C'}} = {S_{ABC}}.CC' = \frac{{4{a^3}\sqrt 3 }}{3}\)

Xét phương trình \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiEamaaCa % aaleqabaGaaGinaaaakiabgkHiTiaaiodacaWG4bWaaWbaaSqabeaa % caaIYaaaaOGaey4kaSIaamyBaiabg2da9iaaicdacqGHuhY2caWG4b % WaaWbaaSqabeaacaaI0aaaaOGaeyOeI0IaaG4maiaadIhadaahaaWc % beqaaiaaikdaaaGccqGHsislcaaIZaGaeyypa0JaeyOeI0IaamyBai % abgkHiTiaaiodaaaa!4D34! {x^4} - 3{x^2} + m = 0 \Leftrightarrow {x^4} - 3{x^2} - 3 = - m - 3\)

Khi đó Dựa vào đồ thị để phương trình đã cho có ba nghiệm thì \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyOeI0Iaam % yBaiabgkHiTiaaiodacqGH9aqpcqGHsislcaaIZaGaeyi1HSTaamyB % aiabg2da9iaaicdaaaa!413B! - m - 3 = - 3 \Leftrightarrow m = 0\).

Đồ thị hàm số có đúng một cực trị khi và chỉ khi \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyyaiaadk % gacqGHLjYScaaIWaGaeyi1HSTaeyOeI0IaamyBamaabmaabaGaaGym % aiabgkHiTiaad2gaaiaawIcacaGLPaaacqGHLjYScaaIWaGaeyi1HS % 9aamqaaqaabeqaaiaad2gacqGHKjYOcaaIWaaabaGaamyBaiabgwMi % ZkaaigdaaaGaay5waaaaaa!4F51! ab \ge 0 \Leftrightarrow - m\left( {1 - m} \right) \ge 0 \Leftrightarrow \left[ \begin{array}{l} m \le 0\\ m \ge 1 \end{array} \right.\).

Xét dãy số \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaeWaaeaaca % WG1bWaaSbaaSqaaiaad6gaaeqaaaGccaGLOaGaayzkaaaaaa!39A0! \left( {{u_n}} \right)\), với \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyDamaaBa % aaleaacaWGUbaabeaakiabg2da9maabmaabaGaaGymaiabgkHiTmaa % laaabaGaaGymaaqaaiaaikdadaahaaWcbeqaaiaaikdaaaaaaaGcca % GLOaGaayzkaaWaaeWaaeaacaaIXaGaeyOeI0YaaSaaaeaacaaIXaaa % baGaaG4mamaaCaaaleqabaGaaGOmaaaaaaaakiaawIcacaGLPaaaca % GGUaGaaiOlaiaac6cadaqadaqaaiaaigdacqGHsisldaWcaaqaaiaa % igdaaeaacaWGUbWaaWbaaSqabeaacaaIYaaaaaaaaOGaayjkaiaawM % caaaaa!4C6C! {u_n} = \left( {1 - \frac{1}{{{2^2}}}} \right)\left( {1 - \frac{1}{{{3^2}}}} \right)...\left( {1 - \frac{1}{{{n^2}}}} \right)\); \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOBaiabgw % MiZkaaikdacaGGSaGaaGPaVlaad6gacqGHiiIZcqWIvesPaaa!3F87! n \ge 2,\,n \in N \)

Ta có:

\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyDamaaBa % aaleaacaaIYaaabeaakiabg2da9iaaigdacqGHsisldaWcaaqaaiaa % igdaaeaacaaIYaWaaWbaaSqabeaacaaIYaaaaaaakiabg2da9maala % aabaGaaG4maaqaaiaaisdaaaGaeyypa0ZaaSaaaeaacaaIYaGaey4k % aSIaaGymaaqaaiaaikdacaGGUaGaaGOmaaaaaaa!4532! {u_2} = 1 - \frac{1}{{{2^2}}} = \frac{3}{4} = \frac{{2 + 1}}{{2.2}}\);

\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyDamaaBa % aaleaacaaIZaaabeaakiabg2da9maabmaabaGaaGymaiabgkHiTmaa % laaabaGaaGymaaqaaiaaikdadaahaaWcbeqaaiaaikdaaaaaaaGcca % GLOaGaayzkaaGaaiOlamaabmaabaGaaGymaiabgkHiTmaalaaabaGa % aGymaaqaaiaaiodadaahaaWcbeqaaiaaikdaaaaaaaGccaGLOaGaay % zkaaGaeyypa0ZaaSaaaeaacaaIZaaabaGaaGinaaaacaGGUaWaaSaa % aeaacaaI4aaabaGaaGyoaaaacqGH9aqpdaWcaaqaaiaaisdaaeaaca % aI2aaaaiabg2da9maalaaabaGaaG4maiabgUcaRiaaigdaaeaacaaI % YaGaaiOlaiaaiodaaaaaaa!51F7! {u_3} = \left( {1 - \frac{1}{{{2^2}}}} \right).\left( {1 - \frac{1}{{{3^2}}}} \right) = \frac{3}{4}.\frac{8}{9} = \frac{4}{6} = \frac{{3 + 1}}{{2.3}}\);

\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyDamaaBa % aaleaacaaI0aaabeaakiabg2da9maabmaabaGaaGymaiabgkHiTmaa % laaabaGaaGymaaqaaiaaikdadaahaaWcbeqaaiaaikdaaaaaaaGcca % GLOaGaayzkaaGaaiOlamaabmaabaGaaGymaiabgkHiTmaalaaabaGa % aGymaaqaaiaaiodadaahaaWcbeqaaiaaikdaaaaaaaGccaGLOaGaay % zkaaWaaeWaaeaacaaIXaGaeyOeI0YaaSaaaeaacaaIXaaabaGaaGin % amaaCaaaleqabaGaaGOmaaaaaaaakiaawIcacaGLPaaacqGH9aqpda % WcaaqaaiaaiodaaeaacaaI0aaaaiaac6cadaWcaaqaaiaaiIdaaeaa % caaI5aaaaiaac6cadaWcaaqaaiaaigdacaaI1aaabaGaaGymaiaaiA % daaaGaeyypa0ZaaSaaaeaacaaI1aaabaGaaGioaaaacqGH9aqpdaWc % aaqaaiaaisdacqGHRaWkcaaIXaaabaGaaGOmaiaac6cacaaI0aaaaa % aa!5B61! {u_4} = \left( {1 - \frac{1}{{{2^2}}}} \right).\left( {1 - \frac{1}{{{3^2}}}} \right)\left( {1 - \frac{1}{{{4^2}}}} \right) = \frac{3}{4}.\frac{8}{9}.\frac{{15}}{{16}} = \frac{5}{8} = \frac{{4 + 1}}{{2.4}}\)

...

\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyDamaaBa % aaleaacaWGUbaabeaakiabg2da9maalaaabaGaamOBaiabgUcaRiaa % igdaaeaacaaIYaGaamOBaaaaaaa!3D6C! {u_n} = \frac{{n + 1}}{{2n}}\)

Dễ dàng chứng minh bằng phương pháp qui nạp để khẳng định \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyDamaaBa % aaleaacaWGUbaabeaakiabg2da9maalaaabaGaamOBaiabgUcaRiaa % igdaaeaacaaIYaGaamOBaaaacaGGSaGaaGPaVlabgcGiIiaad6gacq % GHLjYScaaIYaaaaa!43EC! {u_n} = \frac{{n + 1}}{{2n}},\,\forall n \ge 2\)

Khi đó .

\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaciiBaiaacM % gacaGGTbWaamWaaeaadaqadaqaaiaaigdacqGHsisldaWcaaqaaiaa % igdaaeaacaaIYaWaaWbaaSqabeaacaaIYaaaaaaaaOGaayjkaiaawM % caamaabmaabaGaaGymaiabgkHiTmaalaaabaGaaGymaaqaaiaaioda % daahaaWcbeqaaiaaikdaaaaaaaGccaGLOaGaayzkaaGaaiOlaiaac6 % cacaGGUaWaaeWaaeaacaaIXaGaeyOeI0YaaSaaaeaacaaIXaaabaGa % amOBamaaCaaaleqabaGaaGOmaaaaaaaakiaawIcacaGLPaaaaiaawU % facaGLDbaacqGH9aqpciGGSbGaaiyAaiaac2gadaWcaaqaaiaad6ga % cqGHRaWkcaaIXaaabaGaaGOmaiaad6gaaaGaeyypa0ZaaSaaaeaaca % aIXaaabaGaaGOmaaaaaaa!58B7! \lim \left[ {\left( {1 - \frac{1}{{{2^2}}}} \right)\left( {1 - \frac{1}{{{3^2}}}} \right)...\left( {1 - \frac{1}{{{n^2}}}} \right)} \right] = \lim \frac{{n + 1}}{{2n}} = \frac{1}{2}\)

Ta có: \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGabmyEayaafa % Gaeyypa0JaeyOeI0IaamiEamaaCaaaleqabaGaaGOmaaaakiabgUca % RiaaikdadaqadaqaaiaadggacqGHsislcaaIXaaacaGLOaGaayzkaa % GaamiEaiabgUcaRiaadggacqGHRaWkcaaIZaaaaa!44FA! y' = - {x^2} + 2\left( {a - 1} \right)x + a + 3\).

Để hàm số đồng biến trên khoảng \((0;3)\) thì \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGabmyEayaafa % GaeyyzImRaaGimaiaacYcacaaMc8UaaGPaVlabgcGiIiaadIhacqGH % iiIZdaqadaqaaiaaicdacaGG7aGaaGPaVlaaykW7caaIZaaacaGLOa % Gaayzkaaaaaa!476A! y' \ge 0,\,\,\forall x \in \left( {0;\,\,3} \right)\)

(Dấu  chỉ xảy ra tại hữu hạn điểm trên \((0;3)\) ).

\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyi1HSTaam % yyaiabgwMiZoaalaaabaGaamiEamaaCaaaleqabaGaaGOmaaaakiab % gUcaRiaaikdacaWG4bGaeyOeI0IaaG4maaqaaiaaikdacaWG4bGaey % 4kaSIaaGymaaaacaGGSaGaaGPaVlabgcGiIiaadIhacqGHiiIZdaqa % daqaaiaaicdacaGG7aGaaGPaVlaaykW7caaIZaaacaGLOaGaayzkaa % Gaeyi1HSTaamyyaiabgwMiZoaaxababaGaciyBaiaacggacaGG4baa % leaadaqadaqaaiaaicdacaGG7aGaaGPaVlaaykW7caaIZaaacaGLOa % GaayzkaaaabeaakiaadAgadaqadaqaaiaadIhaaiaawIcacaGLPaaa % aaa!635D! \Leftrightarrow a \ge \frac{{{x^2} + 2x - 3}}{{2x + 1}},\,\forall x \in \left( {0;\,\,3} \right) \Leftrightarrow a \ge \mathop {\max }\limits_{\left( {0;\,\,3} \right)} f\left( x \right)\).

Xét hàm số \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOzamaabm % aabaGaamiEaaGaayjkaiaawMcaaiabg2da9maalaaabaGaamiEamaa % CaaaleqabaGaaGOmaaaakiabgUcaRiaaikdacaWG4bGaeyOeI0IaaG % 4maaqaaiaaikdacaWG4bGaey4kaSIaaGymaaaaaaa!4406! f\left( x \right) = \frac{{{x^2} + 2x - 3}}{{2x + 1}}\) trên khoảng \((0;3)\)

Ta có \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGabmOzayaafa % WaaeWaaeaacaWG4baacaGLOaGaayzkaaGaeyypa0ZaaSaaaeaacaaI % YaGaamiEamaaCaaaleqabaGaaGOmaaaakiabgUcaRiaaikdacaWG4b % Gaey4kaSIaaGioaaqaamaabmaabaGaaGOmaiaadIhacqGHRaWkcaaI % XaaacaGLOaGaayzkaaWaaWbaaSqabeaacaaIYaaaaaaakiabg2da9m % aalaaabaGaaGOmamaabmaabaGaamiEaiabgUcaRmaalaaabaGaaGym % aaqaaiaaikdaaaaacaGLOaGaayzkaaWaaWbaaSqabeaacaaIYaaaaO % Gaey4kaSYaaSaaaeaacaaIXaGaaGynaaqaaiaaikdaaaaabaWaaeWa % aeaacaaIYaGaamiEaiabgUcaRiaaigdaaiaawIcacaGLPaaadaahaa % WcbeqaaiaaikdaaaaaaOGaeyOpa4JaaGimaiaacYcacaaMc8UaaGPa % VlabgcGiIiaadIhacqGHiiIZdaqadaqaaiaaicdacaGG7aGaaGPaVl % aaykW7caaIZaaacaGLOaGaayzkaaaaaa!67A0! f'\left( x \right) = \frac{{2{x^2} + 2x + 8}}{{{{\left( {2x + 1} \right)}^2}}} = \frac{{2{{\left( {x + \frac{1}{2}} \right)}^2} + \frac{{15}}{2}}}{{{{\left( {2x + 1} \right)}^2}}} > 0,\,\,\forall x \in \left( {0;\,\,3} \right)\).

 \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyO0H4Taam % OzamaabmaabaGaamiEaaGaayjkaiaawMcaaaaa!3BC2! \Rightarrow f\left( x \right)\) luôn đồng biến trên khoảng \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaeWaaeaaca % aIWaGaai4oaiaaykW7caaMc8UaaG4maaGaayjkaiaawMcaaiabgkDi % EpaaxababaGaciyBaiaacggacaGG4baaleaadaqadaqaaiaaicdaca % GG7aGaaGPaVlaaykW7caaIZaaacaGLOaGaayzkaaaabeaakiaadAga % daqadaqaaiaadIhaaiaawIcacaGLPaaacqGH9aqpcaWGMbWaaeWaae % aacaaIZaaacaGLOaGaayzkaaGaeyypa0ZaaSaaaeaacaaIXaGaaGOm % aaqaaiaaiEdaaaaaaa!5408! \left( {0;\,\,3} \right) \Rightarrow \mathop {\max }\limits_{\left( {0;\,\,3} \right)} f\left( x \right) = f\left( 3 \right) = \frac{{12}}{7}\).

Vậy \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyBaiabgw % MiZoaalaaabaGaaGymaiaaikdaaeaacaaI3aaaaaaa!3AF4! m \ge \frac{{12}}{7}\).

Xét phương trình \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyyaiGaco % hacaGGPbGaaiOBaiaadIhacqGHRaWkcaWGIbGaci4yaiaac+gacaGG % ZbGaamiEaiabgUcaRiaadogacqGH9aqpcaaIWaaaaa!43D1! a\sin x + b\cos x + c = 0\) có nghiệm khi \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyyamaaCa % aaleqabaGaaGOmaaaakiabgUcaRiaadkgadaahaaWcbeqaaiaaikda % aaGccqGHLjYScaWGJbWaaWbaaSqabeaacaaIYaaaaaaa!3E1F! {a^2} + {b^2} \ge {c^2}\). Vậy để phương trình vô nghiệm thì \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyyamaaCa % aaleqabaGaaGOmaaaakiabgUcaRiaadkgadaahaaWcbeqaaiaaikda % aaGccqGH8aapcaWGJbWaaWbaaSqabeaacaaIYaaaaaaa!3D5D! {a^2} + {b^2} < {c^2}\).

Ta có: \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaaGOmaiGaco % hacaGGPbGaaiOBamaaCaaaleqabaGaaGOmaaaakiaadIhacqGHRaWk % caWGTbGaaiOlaiGacohacaGGPbGaaiOBaiaaikdacaWG4bGaeyypa0 % JaaGOmaiaad2gaaaa!4542! 2{\sin ^2}x + m.\sin 2x = 2m\)\(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyi1HSTaaG % ymaiabgkHiTiGacogacaGGVbGaai4CaiaaikdacaWG4bGaey4kaSIa % amyBaiaac6caciGGZbGaaiyAaiaac6gacaaIYaGaamiEaiabg2da9i % aaikdacaWGTbaaaa!484E! \Leftrightarrow 1 - \cos 2x + m.\sin 2x = 2m\)

\(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyi1HSTaam % yBaiaac6caciGGZbGaaiyAaiaac6gacaaIYaGaamiEaiabgkHiTiGa % cogacaGGVbGaai4CaiaaikdacaWG4bGaeyOeI0IaaGOmaiaad2gacq % GHRaWkcaaIXaGaeyypa0JaaGimaaaa!49F5! \Leftrightarrow m.\sin 2x - \cos 2x - 2m + 1 = 0\) (*)

Để phương trình (*) vô nghiệm thì:

\(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyBamaaCa % aaleqabaGaaGOmaaaakiabgUcaRmaabmaabaGaeyOeI0IaaGymaaGa % ayjkaiaawMcaamaaCaaaleqabaGaaGOmaaaakiabgYda8maabmaaba % GaeyOeI0IaaGOmaiaad2gacqGHRaWkcaaIXaaacaGLOaGaayzkaaWa % aWbaaSqabeaacaaIYaaaaaaa!448C! {m^2} + {\left( { - 1} \right)^2} < {\left( { - 2m + 1} \right)^2}\) \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyi1HSTaaG % 4maiaad2gadaahaaWcbeqaaiaaikdaaaGccqGHsislcaaI0aGaamyB % aiabg6da+iaaicdaaaa!3F50! \Leftrightarrow 3{m^2} - 4m > 0\)\(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyi1HS9aam % qaaqaabeqaaiaad2gacqGH8aapcaaIWaaabaGaamyBaiabg6da+maa % laaabaGaaGinaaqaaiaaiodaaaaaaiaawUfaaaaa!3F86! \Leftrightarrow \left[ \begin{array}{l} m < 0\\ m > \frac{4}{3} \end{array} \right.\)

Chất điểm chuyển động theo quy luật \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4uamaabm % aabaGaamiDaaGaayjkaiaawMcaaiabg2da9iaaigdacqGHRaWkcaaI % ZaGaamiDamaaCaaaleqabaGaaGOmaaaakiabgkHiTiaadshadaahaa % Wcbeqaaiaaiodaaaaaaa!4169! S\left( t \right) = 1 + 3{t^2} - {t^3}\) . Vì vận tốc của chuyển động ở thời điểm t chính là \(S'(t)\); ta đi tìm giá trị lớn nhất của hàm số \(S'(t)\).

Ta có  \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGabm4uayaafa % WaaeWaaeaacaWG0baacaGLOaGaayzkaaGaeyypa0ZaaeWaaeaacaaI % XaGaey4kaSIaaG4maiaadshadaahaaWcbeqaaiaaikdaaaGccqGHsi % slcaWG0bWaaWbaaSqabeaacaaIZaaaaaGccaGLOaGaayzkaaWaaWba % aSqabeaakiadacUHYaIOaaGaeyypa0JaaGOnaiaadshacqGHsislca % aIZaGaamiDamaaCaaaleqabaGaaGOmaaaaaaa!4C72! S'\left( t \right) = {\left( {1 + 3{t^2} - {t^3}} \right)^\prime } = 6t - 3{t^2}\)\(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyypa0Jaey % OeI0IaaG4mamaabmaabaGaamiDamaaCaaaleqabaGaaGOmaaaakiab % gkHiTiaaikdacaWG0baacaGLOaGaayzkaaaaaa!3EBA! = - 3\left( {{t^2} - 2t} \right)\)\(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyypa0JaaG % 4maiabgkHiTiaaiodadaqadaqaaiaadshacqGHsislcaaIXaaacaGL % OaGaayzkaaWaaWbaaSqabeaacaaIYaaaaOGaeyizImQaaG4maiaacY % cacqGHaiIicaWG0bGaeyicI4SaeSyhHekaaa!465C! = 3 - 3{\left( {t - 1} \right)^2} \le 3,\forall t \in R\)

\(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaCbeaeaaci % GGTbGaaiyyaiaacIhaaSqaaiabl2riHcqabaGcceWGtbGbauaadaqa % daqaaiaadshaaiaawIcacaGLPaaacqGH9aqpcaaIZaaaaa!3FA3! \mathop {\max }\limits_ RS'\left( t \right) = 3\) khi \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiDaiabgk % HiTiaaigdacqGH9aqpcaaIWaGaeyi1HSTaamiDaiabg2da9iaaigda % aaa!3F6A! t - 1 = 0 \Leftrightarrow t = 1\)

Vậy Chọn B.

Quan sát đồ thị của hàm số \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9iaadggacaWG4bWaaWbaaSqabeaacaaIZaaaaOGaey4kaSIaamOy % aiaadIhadaahaaWcbeqaaiaaikdaaaGccqGHRaWkcaWGJbGaamiEai % abgUcaRiaadsgadaqadaqaaiaadggacqGHGjsUcaaIWaaacaGLOaGa % ayzkaaaaaa!4809! y = a{x^3} + b{x^2} + cx + d\left( {a \ne 0} \right)\) luôn luôn có một điểm uốn và một tâm đối xứng, loại B và C.

\(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9maabmaabaGaaGymaiabgkHiTiaadIhaaiaawIcacaGLPaaadaqa % daqaaiaadIhacqGHRaWkcaaIYaaacaGLOaGaayzkaaWaaWbaaSqabe % aacaaIYaaaaaaa!4132! y = \left( {1 - x} \right){\left( {x + 2} \right)^2}\) \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyypa0Jaey % OeI0IaamiEamaaCaaaleqabaGaaG4maaaakiabgkHiTiaaiodacaWG % 4bWaaWbaaSqabeaacaaIYaaaaOGaey4kaSIaaGinaaaa!3F11! = - {x^3} - 3{x^2} + 4\)\(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyO0H4Tabm % yEayaafaGaeyypa0JaeyOeI0IaaG4maiaadIhadaahaaWcbeqaaiaa % ikdaaaGccqGHsislcaaI2aGaamiEaiabg2da9iaaicdacqGHshI3aa % a!44C1! \Rightarrow y' = - 3{x^2} - 6x = 0 \Rightarrow \) \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaamqaaqaabe % qaaiaadIhacqGH9aqpcaaIWaaabaGaamiEaiabg2da9iabgkHiTiaa % ikdaaaGaay5waaaaaa!3D5E! \left[ \begin{array}{l} x = 0\\ x = - 2 \end{array} \right.\)( có hai nghiệm phân biệt).

Vậy (C) có hai điểm cực trị nên loại A. Chọn D

Gọi t là số lần giảm \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaeWaaeaaca % aIWaGaeyizImQaamiDaiabgsMiJkaaisdacaGG7aGaamiDaiabgIGi % olabl2riHcGaayjkaiaawMcaaaaa!4203! \left( {0 \le t \le 4;t \in R } \right)\) thì 5000t  là tổng số tiền giảm. Lúc đó giá bán sẽ là 50000 - 5000t , số quả bưởi bán ra là 40 + + 50t suy ra tổng số tiền bán được cả vốn lẫn lãi là \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaeWaaeaaca % aI1aGaaGimaiaaicdacaaIWaGaaGimaiabgkHiTiaaiwdacaaIWaGa % aGimaiaaicdacaWG0baacaGLOaGaayzkaaGaaiOlamaabmaabaGaaG % inaiaaicdacqGHRaWkcaaI1aGaaGimaiaadshaaiaawIcacaGLPaaa % aaa!46FD! \left( {50000 - 5000t} \right).\left( {40 + 50t} \right)\); số tiền vốn nhập ban đầu là \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaaG4maiaaic % dacaaIWaGaaGimaiaaicdacaGGUaWaaeWaaeaacaaI0aGaaGimaiab % gUcaRiaaiwdacaaIWaGaamiDaaGaayjkaiaawMcaaaaa!409F! 30000.\left( {40 + 50t} \right)\).

Ta có lợi nhuận thu được là \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOzamaabm % aabaGaamiDaaGaayjkaiaawMcaaiabg2da9maabmaabaGaaGynaiaa % icdacaaIWaGaaGimaiaaicdacqGHsislcaaI1aGaaGimaiaaicdaca % aIWaGaamiDaaGaayjkaiaawMcaamaabmaabaGaaGinaiaaicdacqGH % RaWkcaaI1aGaaGimaiaadshaaiaawIcacaGLPaaacqGHsislcaaIZa % GaaGimaiaaicdacaaIWaGaaGimamaabmaabaGaaGinaiaaicdacqGH % RaWkcaaI1aGaaGimaiaadshaaiaawIcacaGLPaaaaaa!55A5! f\left( t \right) = \left( {50000 - 5000t} \right)\left( {40 + 50t} \right) - 30000\left( {40 + 50t} \right)\).

Ta tìm t để f(t) lớn nhất: \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOzamaabm % aabaGaamiDaaGaayjkaiaawMcaaiabg2da9maabmaabaGaaGinaiab % gUcaRiaaiwdacaWG0baacaGLOaGaayzkaaWaaeWaaeaacaaIYaGaaG % imaiabgkHiTiaaiwdacaWG0baacaGLOaGaayzkaaGaaiOlaiaaigda % caaIWaGaaGimaiaaicdacaaIWaaaaa!4940! f\left( t \right) = \left( {4 + 5t} \right)\left( {20 - 5t} \right).10000\)

\(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyO0H4Taam % 4zamaabmaabaGaamiDaaGaayjkaiaawMcaaiabg2da9maalaaabaGa % amOzamaabmaabaGaamiDaaGaayjkaiaawMcaaaqaaiaaigdacaaIWa % GaaGimaiaaicdacaaIWaaaaiabg2da9iabgkHiTiaaikdacaaI1aGa % amiDamaaCaaaleqabaGaaGOmaaaakiabgUcaRiaaiIdacaaIWaGaam % iDaiabgUcaRiaaiIdacaaIWaaaaa!4EF3! \Rightarrow g\left( t \right) = \frac{{f\left( t \right)}}{{10000}} = - 25{t^2} + 80t + 80\) \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyypa0JaaG % ymaiaaisdacaaI0aGaeyOeI0YaaeWaaeaacaaI1aGaamiDaiabgkHi % TiaaiIdaaiaawIcacaGLPaaadaahaaWcbeqaaiaaikdaaaGccqGHKj % YOcaaIXaGaaGinaiaaisdacaGGSaGaeyiaIiIaamiDaiabgIGiolab % l2riHcaa!4959! = 144 - {\left( {5t - 8} \right)^2} \le 144,\forall t \in R\)

Để f(t) lớn nhất khi g(t) lớn nhất; g(t0 lớn nhất bằng 144 khi \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaaGynaiaads % hacqGHsislcaaI4aGaeyypa0JaaGimaiabgsDiBlaadshacqGH9aqp % daWcaaqaaiaaiIdaaeaacaaI1aaaaaaa!4106! 5t - 8 = 0 \Leftrightarrow t = \frac{8}{5}\)

\(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiDaiabg2 % da9maalaaabaGaaGioaaqaaiaaiwdaaaGaeyO0H4TaaGynaiaaicda % caaIWaGaaGimaiaadshacqGH9aqpcaaI4aGaaGimaiaaicdacaaIWa % aaaa!43BC! t = \frac{8}{5} \Rightarrow 5000t = 8000\). Do đó giảm số tiền một quả bưởi là 8000  đồng , tức giá bán ra một quả là 50000 - 8000 = 42000 đông thì lợi nhuận thu được cao nhất.

Xét hình chóp tam giác đều S.ABC . Gọi  M là trung điểm BC , G là trọng tâm của tam giác đều ABC cạnh a thì \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyqaiaad2 % eacqGH9aqpdaWcaaqaaiaadggadaGcaaqaaiaaiodaaSqabaaakeaa % caaIYaaaaaaa!3B25! AM = \frac{{a\sqrt 3 }}{2}\) ; \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4uaiaadE % eacqGHLkIxdaqadaqaaiaadgeacaWGcbGaam4qaaGaayjkaiaawMca % aaaa!3D26! SG \bot \left( {ABC} \right)\),   SG là chiều cao của hình chóp nên \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaecaaeaaca % WGtbGaamyqaiaadEeaaiaawkWaaiabg2da9iabeA8aQbaa!3BE2! \widehat {SAG} = \varphi \).

Ta có: \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4uamaaBa % aaleaacqGHuoarcaWGbbGaamOqaiaadoeaaeqaaOGaeyypa0ZaaSaa % aeaacaaIXaaabaGaaGOmaaaacaWGbbGaamytaiaac6cacaWGcbGaam % 4qaiabg2da9maalaaabaGaaGymaaqaaiaaikdaaaGaeyyXIC9aaSaa % aeaacaWGHbWaaWbaaSqabeaacaaIYaaaaOWaaOaaaeaacaaIZaaale % qaaaGcbaGaaGOmaaaacqGH9aqpdaWcaaqaaiaadggadaahaaWcbeqa % aiaaikdaaaGcdaGcaaqaaiaaiodaaSqabaaakeaacaaI0aaaaaaa!4E10! {S_{\Delta ABC}} = \frac{1}{2}AM.BC = \frac{1}{2} \cdot \frac{{{a^2}\sqrt 3 }}{2} = \frac{{{a^2}\sqrt 3 }}{4}\)

Xét tam giác SAG vuông tại G, \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaecaaeaaca % WGtbGaamyqaiaadEeaaiaawkWaaiabg2da9iabeA8aQbaa!3BE2! \widehat {SAG} = \varphi \), \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyqaiaadE % eacqGH9aqpdaWcaaqaaiaaikdaaeaacaaIZaaaaiaadgeacaWGnbGa % eyypa0ZaaSaaaeaacaWGHbWaaOaaaeaacaaIZaaaleqaaaGcbaGaaG % 4maaaaaaa!3F47! AG = \frac{2}{3}AM = \frac{{a\sqrt 3 }}{3}\):\(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4uaiaadE % eacqGH9aqpcaWGbbGaam4raiaac6caciGG0bGaaiyyaiaac6gacqaH % gpGAcqGH9aqpdaWcaaqaaiaadggadaGcaaqaaiaaiodaaSqabaGcci % GG0bGaaiyyaiaac6gacqaHgpGAaeaacaaIZaaaaaaa!4798! SG = AG.\tan \varphi = \frac{{a\sqrt 3 \tan \varphi }}{3}\)

Vậy thể tích hình chóp S.ABC: \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOvaiabg2 % da9maalaaabaGaaGymaaqaaiaaiodaaaGaam4uaiaadEeacaGGUaGa % am4uamaaBaaaleaacqGHuoarcaWGbbGaamOqaiaadoeaaeqaaOGaey % ypa0ZaaSaaaeaacaaIXaaabaGaaG4maaaacqGHflY1daWcaaqaaiaa % dggadaGcaaqaaiaaiodaaSqabaGcciGG0bGaaiyyaiaac6gacqaHgp % GAaeaacaaIZaaaaiabgwSixpaalaaabaGaamyyamaaCaaaleqabaGa % aGOmaaaakmaakaaabaGaaG4maaWcbeaaaOqaaiaaisdaaaGaeyypa0 % ZaaSaaaeaacaWGHbWaaWbaaSqabeaacaaIZaaaaOGaciiDaiaacgga % caGGUbGaeqOXdOgabaGaaGymaiaaikdaaaaaaa!5B3F! V = \frac{1}{3}SG.{S_{\Delta ABC}} = \frac{1}{3} \cdot \frac{{a\sqrt 3 \tan \varphi }}{3} \cdot \frac{{{a^2}\sqrt 3 }}{4} = \frac{{{a^3}\tan \varphi }}{{12}}\) .

Trong mặt phẳng (SBC) . Qua G kẻ đường thẳng song song với BC và lần lượt cắt SC, SB  tại E, F . Khi đó ta được khối đa diện không chứa đỉnh S là ABCEF

Ta có G là trọng tâm của \(\Delta SBC\) nên \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaaca % WGwbWaaSbaaSqaaiaadofacaGGUaGaaeyqaiaabAeacaWGfbaabeaa % aOqaaiaadAfadaWgaaWcbaGaam4uaiaac6cacaWGbbGaamOqaiaado % eaaeqaaaaakiabg2da9maalaaabaGaam4uaiaadgeaaeaacaWGtbGa % amyqaaaacaGGUaWaaSaaaeaacaWGtbGaamOraaqaaiaadofacaWGcb % aaaiaac6cadaWcaaqaaiaadofacaWGfbaabaGaam4uaiaadoeaaaGa % eyypa0ZaaSaaaeaacaaIYaaabaGaaG4maaaacaGGUaWaaSaaaeaaca % aIYaaabaGaaG4maaaacqGH9aqpdaWcaaqaaiaaisdaaeaacaaI5aaa % aiaac6caaaa!5452! \frac{{{V_{S.{\rm{AF}}E}}}}{{{V_{S.ABC}}}} = \frac{{SA}}{{SA}}.\frac{{SF}}{{SB}}.\frac{{SE}}{{SC}} = \frac{2}{3}.\frac{2}{3} = \frac{4}{9}.\)

Do đó: \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOvamaaBa % aaleaacaWGtbGaaiOlaiaabgeacaqGgbGaamyraaqabaGccqGH9aqp % daWcaaqaaiaaisdaaeaacaaI5aaaaiaac6cacaWGwbWaaSbaaSqaai % aadofacaGGUaGaamyqaiaadkeacaWGdbaabeaakiabgkDiElaadAfa % daWgaaWcbaGaamyqaiaadkeacaWGdbGaamyraiaadAeaaeqaaOGaey % ypa0JaamOvamaaBaaaleaadaWgaaadbaGaam4uaiaac6cacaWGbbGa % amOqaiaadoeaaeqaaaWcbeaakiabgkHiTmaalaaabaGaaGinaaqaai % aaiMdaaaGaaiOlaiaadAfadaWgaaWcbaGaam4uaiaac6cacaWGbbGa % amOqaiaadoeaaeqaaOGaeyypa0ZaaSaaaeaacaaI1aaabaGaaGyoaa % aacaGGUaGaamOvamaaBaaaleaacaWGtbGaaiOlaiaadgeacaWGcbGa % am4qaaqabaGccaGGUaaaaa!61B0! {V_{S.{\rm{AF}}E}} = \frac{4}{9}.{V_{S.ABC}} \Rightarrow {V_{ABCEF}} = {V_{_{S.ABC}}} - \frac{4}{9}.{V_{S.ABC}} = \frac{5}{9}.{V_{S.ABC}}.\)

Vì tam giác \(\Delta ABC\) vuông cân ở B, \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyqaiaado % eacqGH9aqpcaWGHbWaaOaaaeaacaaIYaaaleqaaaaa!3A44! AC = a\sqrt 2 \) nên AB = BC = a

Mặt khác \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOvamaaBa % aaleaacaWGtbGaaiOlaiaadgeacaWGcbGaam4qaaqabaGccqGH9aqp % daWcaaqaaiaaigdaaeaacaaIZaaaamaalaaabaGaaGymaaqaaiaaik % daaaGaamyyaiaac6cacaWGHbGaaiOlaiaadggacqGH9aqpdaWcaaqa % aiaadggadaahaaWcbeqaaiaaiodaaaaakeaacaaI2aaaaiaac6caaa % a!4770! {V_{S.ABC}} = \frac{1}{3}\frac{1}{2}a.a.a = \frac{{{a^3}}}{6}.\) Suy ra \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOvamaaBa % aaleaacaWGbbGaamOqaiaadoeacaWGfbGaamOraaqabaGccqGH9aqp % daWcaaqaaiaaiwdaaeaacaaI5aaaaiaac6cadaWcaaqaaiaadggada % ahaaWcbeqaaiaaiodaaaaakeaacaaI2aaaaiabg2da9maalaaabaGa % aGynaiaadggadaahaaWcbeqaaiaaiodaaaaakeaacaaI1aGaaGinaa % aaaaa!460E! {V_{ABCEF}} = \frac{5}{9}.\frac{{{a^3}}}{6} = \frac{{5{a^3}}}{{54}}\) .

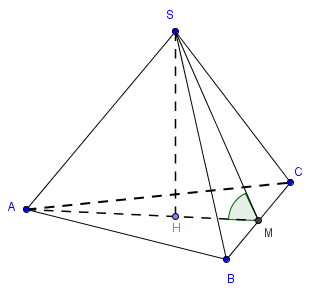
Gọi M là trung điểm của BC

Vì \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaiqaaqaabe % qaamaabmaabaGaam4uaiaadkeacaWGdbaacaGLOaGaayzkaaGaeyyk % IC8aaeWaaeaacaWGbbGaamOqaiaadoeaaiaawIcacaGLPaaacqGH9a % qpcaWGcbGaam4qaaqaaiaadofacaWGnbGaeyOGIW8aaeWaaeaacaWG % tbGaamOqaiaadoeaaiaawIcacaGLPaaacaGG6aGaam4uaiaad2eacq % GHLkIxcaWGcbGaam4qaaqaaiaadgeacaWGnbGaeyOGIW8aaeWaaeaa % caWGbbGaamOqaiaadoeaaiaawIcacaGLPaaacaGG6aGaamyqaiaad2 % eacqGHLkIxcaWGcbGaam4qaaaacaGL7baaaaa!5D5D! \left\{ \begin{array}{l} \left( {SBC} \right) \cap \left( {ABC} \right) = BC\\ SM \subset \left( {SBC} \right):SM \bot BC\\ AM \subset \left( {ABC} \right):AM \bot BC \end{array} \right.\).\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyO0H49aae % caaeaacaWGtbGaamyqaiaad2eaaiaawkWaaiabg2da9iaaiAdacaaI % WaWaaWbaaSqabeaacaqGVbaaaaaa!3F22! \Rightarrow \widehat {SAM} = {60^{\rm{o}}}\) 

Gọi H là trọng tâm tam giác ABC . Vì S.ABC là hình chóp đều nên \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4uaiaadI % eacqGHLkIxdaqadaqaaiaadgeacaWGcbGaam4qaaGaayjkaiaawMca % aaaa!3D27! SH \bot \left( {ABC} \right)\).

Trong tam giác SHM vuông có  \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4uaiaadI % eacqGH9aqpcaWGibGaamytaiaac6caciGG0bGaaiyyaiaac6gacaaI % 2aGaaGimaiabgclaWkabg2da9maalaaabaGaamyyamaakaaabaGaaG % 4maaWcbeaaaOqaaiaaiAdaaaGaaiOlamaakaaabaGaaG4maaWcbeaa % kiabg2da9maalaaabaGaamyyaaqaaiaaikdaaaGaaiOlaaaa!49C2! SH = HM.\tan 60^\circ = \frac{{a\sqrt 3 }}{6}.\sqrt 3 = \frac{a}{2}.\)

ĐK \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiEaiabgI % GiopaadmaabaGaeyOeI0IaaGinaiaacUdacaaMc8UaaGinaaGaay5w % aiaaw2faaaaa!3F1A! x \in \left[ { - 4;\,4} \right]\). Đặt \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiDaiabg2 % da9maakaaabaGaaGinaiabgkHiTiaadIhaaSqabaGccqGHRaWkdaGc % aaqaaiaaisdacqGHRaWkcaWG4baaleqaaaaa!3E5A! t = \sqrt {4 - x} + \sqrt {4 + x} \) , ta có \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiDaiabgI % GiopaadmaabaGaaGOmamaakaaabaGaaGOmaaWcbeaakiaacUdacaaM % c8UaaGinaaGaay5waiaaw2faaaaa!3F08! t \in \left[ {2\sqrt 2 ;\,4} \right]\).

Ta có  \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiDamaaCa % aaleqabaGaaGOmaaaakiabg2da9iaaikdadaGcaaqaaiaaigdacaaI % 2aGaeyOeI0IaamiEamaaCaaaleqabaGaaGOmaaaaaeqaaOGaey4kaS % IaaGioaaaa!3FAE! {t^2} = 2\sqrt {16 - {x^2}} + 8\)\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyi1HSTaaG % OmamaakaaabaGaaGymaiaaiAdacqGHsislcaWG4bWaaWbaaSqabeaa % caaIYaaaaaqabaGccqGH9aqpcaWG0bWaaWbaaSqabeaacaaIYaaaaO % GaeyOeI0IaaGioaiaac6caaaa!42C7! \Leftrightarrow 2\sqrt {16 - {x^2}} = {t^2} - 8.\)

Phương trình đã cho trở thành \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiDamaaCa % aaleqabaGaaG4maaaakiabgkHiTiaaiodadaqadaqaaiaadshadaah % aaWcbeqaaiaaikdaaaGccqGHsislcaaI4aaacaGLOaGaayzkaaGaey % 4kaSIaaGOmaiaad2gacqGHRaWkcaaIXaGaeyypa0JaaGimaaaa!449C! {t^3} - 3\left( {{t^2} - 8} \right) + 2m + 1 = 0\) \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyi1HSTaaG % Omaiaad2gacqGH9aqpcqGHsislcaWG0bWaaWbaaSqabeaacaaIZaaa % aOGaey4kaSIaaG4maiaadshadaahaaWcbeqaaiaaikdaaaGccqGHsi % slcaaIYaGaaGynaiaac6caaaa!4483! \Leftrightarrow 2m = - {t^3} + 3{t^2} - 25.\)

Xét hàm số: \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOzamaabm % aabaGaamiDaaGaayjkaiaawMcaaiabg2da9iabgkHiTiaadshadaah % aaWcbeqaaiaaiodaaaGccqGHRaWkcaaIZaGaamiDamaaCaaaleqaba % GaaGOmaaaakiabgkHiTiaaikdacaaI1aGaeyO0H4TabmOzayaafaWa % aeWaaeaacaWG0baacaGLOaGaayzkaaGaeyypa0JaeyOeI0IaaG4mai % aadshadaahaaWcbeqaaiaaikdaaaGccqGHRaWkcaaI2aGaamiDaiaa % c6caaaa!50F3! f\left( t \right) = - {t^3} + 3{t^2} - 25 \Rightarrow f'\left( t \right) = - 3{t^2} + 6t.\)

Ta có: \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGabmOzayaafa % WaaeWaaeaacaWG0baacaGLOaGaayzkaaGaeyypa0JaeyOeI0IaaG4m % aiaadshadaahaaWcbeqaaiaaikdaaaGccqGHRaWkcaaI2aGaamiDai % abgYda8iaaicdacaGGSaGaaGjbVlabgcGiIiaadshacqGHiiIZdaWa % daqaaiaaikdadaGcaaqaaiaaikdaaSqabaGccaGG7aGaaGPaVlaais % daaiaawUfacaGLDbaaaaa!4E83! f'\left( t \right) = - 3{t^2} + 6t < 0,\;\forall t \in \left[ {2\sqrt 2 ;\,4} \right]\) nên phương trình có nghiệm khi và chỉ khi

 \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOzamaabm % aabaGaaGinaaGaayjkaiaawMcaaiabgsMiJkaaikdacaWGTbGaeyiz % ImQaamOzamaabmaabaGaaGOmamaakaaabaGaaGOmaaWcbeaaaOGaay % jkaiaawMcaaiabgsDiBdaa!44AB! f\left( 4 \right) \le 2m \le f\left( {2\sqrt 2 } \right) \Leftrightarrow \)\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyOeI0IaaG % inaiaaigdacqGHKjYOcaaIYaGaamyBaiabgsMiJkabgkHiTiaaigda % cqGHsislcaaIXaGaaGOnamaakaaabaGaaGOmaaWcbeaaaaa!4259! - 41 \le 2m \le - 1 - 16\sqrt 2 \)\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyi1HSTaey % OeI0YaaSaaaeaacaaI0aGaaGymaaqaaiaaikdaaaGaeyizImQaamyB % aiabgsMiJoaalaaabaGaeyOeI0IaaGymaiabgkHiTiaaigdacaaI2a % WaaOaaaeaacaaIYaaaleqaaaGcbaGaaGOmaaaacaGGUaaaaa!464D! \Leftrightarrow - \frac{{41}}{2} \le m \le \frac{{ - 1 - 16\sqrt 2 }}{2}.\)

Ta có: \( {\sin ^2}x + \sin x = 0\)\(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyi1HS9aam % qaaqaabeqaaiGacohacaGGPbGaaiOBaiaadIhacqGH9aqpcaaIWaaa % baGaci4CaiaacMgacaGGUbGaamiEaiabg2da9iabgkHiTiaaigdaaa % Gaay5waaaaaa!4569! \Leftrightarrow \left[ \begin{array}{l} \sin x = 0\\ \sin x = - 1 \end{array} \right.\)\( \Leftrightarrow \left[ \begin{array}{l} x = k\pi \\ x = - \frac{\pi }{2} + k2\pi \end{array} \right.;k \in Z\)

Đối chiếu với điều kiện \( - \frac{\pi }{2} < x < \frac{\pi }{2}.\) Ta được nghiệm của phương trình là x = 0 

Ta có: \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyOeI0IaaG % ymaiabgsMiJkGacogacaGGVbGaai4CamaabmaabaWaaSaaaeaacqaH % apaCaeaacaaI2aaaaiaadshacqGHRaWkdaWcaaqaaiabec8aWbqaai % aaiodaaaaacaGLOaGaayzkaaGaeyizImQaaGymaaaa!470F! - 1 \le \cos \left( {\frac{\pi }{6}t + \frac{\pi }{3}} \right) \le 1\) \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyi1HSTaaG % yoaiabgsMiJkaadIgacqGHKjYOcaaIXaGaaGynaaaa!3EE4! \Leftrightarrow 9 \le h \le 15\). Do đó mực nước cao nhất của kênh là 15m đạt được khi  \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaci4yaiaac+ % gacaGGZbWaaeWaaeaadaWcaaqaaiabec8aWbqaaiaaiAdaaaGaamiD % aiabgUcaRmaalaaabaGaeqiWdahabaGaaG4maaaaaiaawIcacaGLPa % aacqGH9aqpcaaIXaaaaa!4303! \cos \left( {\frac{\pi }{6}t + \frac{\pi }{3}} \right) = 1\)\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyi1HS9aaS % aaaeaacqaHapaCaeaacaaI2aaaaiaadshacqGHRaWkdaWcaaqaaiab % ec8aWbqaaiaaiodaaaGaeyypa0Jaam4AaiaaikdacqaHapaCaaa!43B1! \Leftrightarrow \frac{\pi }{6}t + \frac{\pi }{3} = k2\pi \)\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyi1HSTaam % iDaiabg2da9iabgkHiTiaaikdacqGHRaWkcaaIXaGaaGOmaiaadUga % aaa!3F41! \Leftrightarrow t = - 2 + 12k\)

Vì \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyi1HSTaey % OeI0IaaGOmaiabgUcaRiaaigdacaaIYaGaam4Aaiabg6da+iaaicda % aaa!3F04! t>0 \Leftrightarrow - 2 + 12k > 0\)\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyi1HSTaam % 4Aaiabg6da+maalaaabaGaaGymaaqaaiaaiAdaaaaaaa!3BD3! \Leftrightarrow k > \frac{1}{6}\)

Chọn số k nguyên dương nhỏ nhất thoả  \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4Aaiabg6 % da+maalaaabaGaaGymaaqaaiaaiAdaaaaaaa!3977! k > \frac{1}{6}\) là \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4Aaiabg2 % da9iaaigdacqGHshI3caWG0bGaeyypa0JaaGymaiaaicdaaaa!3E76! k = 1 \Rightarrow t = 10\)

Gọi E là trung điểm của BB'. Khi đó: \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyraiaad2 % eacaaMi8UaaGjbVlaab+cacaqGVaGaaGjbVlqadkeagaqbaiaadoea % aaa!3F39! EM{\kern 1pt} \;{\rm{//}}\;B'C\)\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyO0H4Tabm % OqayaafaGaam4qaiaayIW7caaMe8Uaae4laiaab+cacaaMe8Uaaiik % aiaadgeacaWGnbGaamyraiaacMcaaaa!43B6! \Rightarrow B'C{\kern 1pt} \;{\rm{//}}\;(AME)\)

Ta có:\(d\left( {AM,B'C} \right) = d\left( {B'C,\left( {AME} \right)} \right) = d\left( {C,\left( {AME} \right)} \right) = d\left( {B,\left( {AME} \right)} \right)\)

Xét khối chóp BAME có các cạnh BE ,AB, BM đôi một vuông góc với nhau nên \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaaca % aIXaaabaGaamizamaaCaaaleqabaGaaGOmaaaakmaabmaabaGaamOq % aiaacYcadaqadaqaaiaadgeacaWGnbGaamyraaGaayjkaiaawMcaaa % GaayjkaiaawMcaaaaacqGH9aqpdaWcaaqaaiaaigdaaeaacaWGbbGa % amOqamaaCaaaleqabaGaaGOmaaaaaaGccqGHRaWkdaWcaaqaaiaaig % daaeaacaWGnbGaamOqamaaCaaaleqabaGaaGOmaaaaaaGccqGHRaWk % daWcaaqaaiaaigdaaeaacaWGfbGaamOqamaaCaaaleqabaGaaGOmaa % aaaaaaaa!4C37! \frac{1}{{{d^2}\left( {B,\left( {AME} \right)} \right)}} = \frac{1}{{A{B^2}}} + \frac{1}{{M{B^2}}} + \frac{1}{{E{B^2}}}\)\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyi1HS9aaS % aaaeaacaaIXaaabaGaamizamaaCaaaleqabaGaaGOmaaaakmaabmaa % baGaamOqaiaacYcadaqadaqaaiaadgeacaWGnbGaamyraaGaayjkai % aawMcaaaGaayjkaiaawMcaaaaacqGH9aqpdaWcaaqaaiaaiEdaaeaa % caWGHbWaaWbaaSqabeaacaaIYaaaaaaaaaa!4588! \Leftrightarrow \frac{1}{{{d^2}\left( {B,\left( {AME} \right)} \right)}} = \frac{7}{{{a^2}}}\)\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyi1HSTaam % izamaaCaaaleqabaGaaGOmaaaakmaabmaabaGaamOqaiaacYcadaqa % daqaaiaadgeacaWGnbGaamyraaGaayjkaiaawMcaaaGaayjkaiaawM % caaiabg2da9maalaaabaGaamyyamaaCaaaleqabaGaaGOmaaaaaOqa % aiaaiEdaaaaaaa!44C7! \Leftrightarrow {d^2}\left( {B,\left( {AME} \right)} \right) = \frac{{{a^2}}}{7}\)\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyi1HSTaam % izamaabmaabaGaamOqaiaacYcadaqadaqaaiaadgeacaWGnbGaamyr % aaGaayjkaiaawMcaaaGaayjkaiaawMcaaiabg2da9maalaaabaGaam % yyaaqaamaakaaabaGaaG4naaWcbeaaaaaaaa!42FC! \Leftrightarrow d\left( {B,\left( {AME} \right)} \right) = \frac{a}{{\sqrt 7 }}\)

.

Chữ số 5 đứng liền giữa hai chữ số 1 và 4 nên ta có thể có 154 hoặc 451

Gọi số cần tìm là \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaa0aaaeaaca % WGHbGaamOyaiaadogaaaaaaa!38BA! \overline {abc} \) (các chữ số khác nhau từng đôi một và a, b, c thuộc \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaiWaaeaaca % aIWaGaaiilaiaaykW7caaIYaGaaiilaiaaykW7caaIZaGaaiilaiaa % ykW7caaI2aGaaiilaiaaykW7caaI3aGaaiilaiaaykW7caaI4aGaai % ilaiaaykW7caaI5aaacaGL7bGaayzFaaaaaa!4AC0! \left\{ {0,\,2,\,3,\,6,\,7,\,8,\,9} \right\}\)), sau đó ta chèn thêm 154 hoặc 451 để có được số gồm 6 chữ số cần tìm.

TH1:\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyyaiabgc % Mi5kaaicdaaaa!395B! a \ne 0\) , số cách chọn a là 6, số cách chọn b và c  là \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyqamaaDa % aaleaacaaI2aaabaGaaGOmaaaaaaa!3863! A_6^2\) , sau đó chèn  154 hoặc 451 vào 4 vị trí còn lại nên có \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaaGOnaiaac6 % cacaWGbbWaa0baaSqaaiaaiAdaaeaacaaIYaaaaOGaaiOlaiaaisda % caGGUaGaaGOmaaaa!3CBD! 6.A_6^2.4.2\) cách

TH2: a = 0, số cách chọn a là 1, số cách chọn b và c là \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyqamaaDa % aaleaacaaI2aaabaGaaGOmaaaaaaa!3863! A_6^2\), sau đó chèn 154 hoặc 451 vào vị trí trước a có duy nhất 1 cách nên có \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyqamaaDa % aaleaacaaI2aaabaGaaGOmaaaakiaac6cacaaIYaaaaa!39DB! A_6^2.2\) cách

Vậy có \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaaGOnaiaac6 % cacaWGbbWaa0baaSqaaiaaiAdaaeaacaaIYaaaaOGaaiOlaiaaisda % caGGUaGaaGOmaiabgUcaRiaadgeadaqhaaWcbaGaaGOnaaqaaiaaik % daaaGccaGGUaGaaGOmaiabg2da9iaaigdacaaI1aGaaGimaiaaicda % aaa!457A! 6.A_6^2.4.2 + A_6^2.2 = 1500\) (số).

Gọi H là trọng tâm tam giác ABC và I là trung điểm BCBC. Ta có:\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaaGPaVlaayk % W7daGabaabaeqabaGabmyqayaafaGaamisaiabgwQiEjaadkeacaWG % dbGaaGPaVdqaaiaadgeacaWGjbGaeyyPI4LaamOqaiaadoeaaeaace % WGbbGbauaacaWGibGaeyykICSaamyqaiaadMeacqGH9aqpcaWGibGa % aGPaVdaacaGL7baacaaMc8UaaGPaVlabgkDiElaadkeacaWGdbGaey % yPI41aaeWaaeaaceWGbbGbauaacaWGbbGaamysaaGaayjkaiaawMca % aiabgkDiElaadkeacaWGdbGaeyyPI4Laamyqaiqadgeagaqbaiaac6 % caaaa!6222! \,\,\left\{ \begin{array}{l} A'H \bot BC\,\\ AI \bot BC\\ A'H \cap AI = H\, \end{array} \right.\,\, \Rightarrow BC \bot \left( {A'AI} \right) \Rightarrow BC \bot AA'.\)

Gọi K là hình chiếu vuông góc của I lên AA'. Khi đó IK là đoạn vuông góc chung của AA' và BC nên \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamysaiaadU % eacaqG9aGaamizamaabmaabaGaamyqaiqadgeagaqbaiaabYcacaqG % GaGaamOqaiaadoeaaiaawIcacaGLPaaacqGH9aqpdaWcaaqaaiaadg % gadaGcaaqaaiaaiodaaSqabaaakeaacaaI0aaaaiaac6caaaa!438A! IK{\rm{ = }}d\left( {AA'{\rm{, }}BC} \right) = \frac{{a\sqrt 3 }}{4}.\)  Xét tam giác vuông AIK vuông tại K có: \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamysaiaadU % eacaqG9aWaaSaaaeaacaWGHbWaaOaaaeaacaaIZaaaleqaaaGcbaGa % aGinaaaacaGGSaGaaGPaVlaaykW7caWGbbGaamysaiabg2da9maala % aabaGaamyyamaakaaabaGaaG4maaWcbeaaaOqaaiaaikdaaaGaeyO0 % H4TaamysaiaadUeacqGH9aqpdaWcaaqaaiaaigdaaeaacaaIYaaaai % aadgeacaWGjbGaeyO0H49aaecaaeaacaWGlbGaamyqaiaadMeaaiaa % wkWaaiabg2da9iaaiodacaaIWaGaeyiSaaRaaiOlaaaa!5695! IK{\rm{ = }}\frac{{a\sqrt 3 }}{4},\,\,AI = \frac{{a\sqrt 3 }}{2} \Rightarrow IK = \frac{1}{2}AI \Rightarrow \widehat {KAI} = 30^\circ .\)

Xét tam giác vuông AA'H vuông tại H có: \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGabmyqayaafa % Gaamisaiaab2dacaWGbbGaamisaiaab6cacaqG0bGaaeyyaiaab6ga % caqGZaGaaeimaiabgclaWkabg2da9maalaaabaGaamyyamaakaaaba % GaaG4maaWcbeaaaOqaaiaaiodaaaGaaiOlamaalaaabaWaaOaaaeaa % caaIZaaaleqaaaGcbaGaaG4maaaacqGH9aqpdaWcaaqaaiaadggaae % aacaaIZaaaaiaac6caaaa!4A1E! A'H{\rm{ = }}AH{\rm{.tan30}}^\circ = \frac{{a\sqrt 3 }}{3}.\frac{{\sqrt 3 }}{3} = \frac{a}{3}.\)

 Vậy: \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaaeOvamaaBa % aaleaacaWGbbGaamOqaiaadoeacaGGUaGabmyqayaafaGabmOqayaa % faGabm4qayaafaaabeaakiabg2da9maalaaabaGaamyyamaaCaaale % qabaGaaGOmaaaakmaakaaabaGaaG4maaWcbeaaaOqaaiaaisdaaaGa % aiOlamaalaaabaGaamyyaaqaaiaaiodaaaGaeyypa0ZaaSaaaeaaca % WGHbWaaWbaaSqabeaacaaIZaaaaOWaaOaaaeaacaaIZaaaleqaaaGc % baGaaGymaiaaikdaaaGaaiOlaaaa!4971! {{\rm{V}}_{ABC.A'B'C'}} = \frac{{{a^2}\sqrt 3 }}{4}.\frac{a}{3} = \frac{{{a^3}\sqrt 3 }}{{12}}.\)

Gọi a,b h,  lần lượt là chiều dài, chiều rộng, chiều cao của hố ga.

Ta có hình vẽ:

Ta có: \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaiqaaqaabe % qaaiaadggacaWGIbGaamiAaiabg2da9iaaiodacaaIYaGaaGimaiaa % icdaaeaadaWcaaqaaiaadIgaaeaacaWGIbaaaiabg2da9iaaikdaaa % Gaay5EaaGaeyi1HS9aaiqaaqaabeqaaiaaikdacaWGHbGaamOyamaa % CaaaleqabaGaaGOmaaaakiabg2da9iaaiodacaaIYaGaaGimaiaaic % daaeaacaWGObGaeyypa0JaaGOmaiaadkgaaaGaay5EaaGaeyi1HS9a % aiqaaqaabeqaaiaadggacqGH9aqpdaWcaaqaaiaaigdacaaI2aGaaG % imaiaaicdaaeaacaWGIbWaaWbaaSqabeaacaaIYaaaaaaaaOqaaiaa % dIgacqGH9aqpcaaIYaGaamOyaaaacaGL7baaaaa!5DC2! \left\{ \begin{array}{l} abh = 3200\\ \frac{h}{b} = 2 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} 2a{b^2} = 3200\\ h = 2b \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} a = \frac{{1600}}{{{b^2}}}\\ h = 2b \end{array} \right.\)

Để xây hố tiết kiệm nguyên vật liệu nhất thì \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4uamaaBa % aaleaacaWG4bGaamyCaaqabaGccqGHRaWkcaWGtbWaaSbaaSqaaiaa % dgraaeqaaaaa!3B72! {S_{xq}} + {S_{đ}}\) đạt giá trị nhỏ nhất.\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4uamaaBa % aaleaacaWG4bGaamyCaaqabaGccqGHRaWkcaWGtbWaaSbaaSqaaiaa % dgraaeqaaOGaeyypa0JaaGOmaiaadkgacaWGObGaey4kaSIaaGOmai % aadggacaWGObGaey4kaSIaamyyaiaadkgacqGH9aqpcaaI0aGaamOy % amaaCaaaleqabaGaaGOmaaaakiabgUcaRmaalaaabaGaaGOnaiaais % dacaaIWaGaaGimaaqaaiaadkgaaaGaey4kaSYaaSaaaeaacaaIXaGa % aGOnaiaaicdacaaIWaaabaGaamOyaaaacqGH9aqpcaaI0aGaamOyam % aaCaaaleqabaGaaGOmaaaakiabgUcaRmaalaaabaGaaGioaiaaicda % caaIWaGaaGimaaqaaiaadkgaaaGaeyypa0JaamOzamaabmaabaGaam % OyaaGaayjkaiaawMcaaaaa!5F2B! {S_{xq}} + {S_{đ}} = 2bh + 2ah + ab = 4{b^2} + \frac{{6400}}{b} + \frac{{1600}}{b} = 4{b^2} + \frac{{8000}}{b} = f\left( b \right)\)

Xét \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOzamaabm % aabaGaamOyaaGaayjkaiaawMcaaiabg2da9iaaisdacaWGIbWaaWba % aSqabeaacaaIYaaaaOGaey4kaSYaaSaaaeaacaaI4aGaaGimaiaaic % dacaaIWaaabaGaamOyaaaaaaa!41B6! f\left( b \right) = 4{b^2} + \frac{{8000}}{b}\) trên \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaeWaaeaaca % aIWaGaai4oaiabgUcaRiabg6HiLcGaayjkaiaawMcaaaaa!3B49! \left( {0; + \infty } \right)\)

Với \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGabmOzayaafa % WaaeWaaeaacaWGIbaacaGLOaGaayzkaaGaeyypa0JaaGioaiaadkga % cqGHsisldaWcaaqaaiaaiIdacaaIWaGaaGimaiaaicdaaeaacaWGIb % WaaWbaaSqabeaacaaIYaaaaaaakiabgkDiElqadAgagaqbamaabmaa % baGaamOyaaGaayjkaiaawMcaaiabg2da9iaaicdacqGHuhY2caaI4a % GaamOyamaaCaaaleqabaGaaG4maaaakiabgkHiTiaaiIdacaaIWaGa % aGimaiaaicdacqGH9aqpcaaIWaGaeyi1HSTaamOyaiabg2da9iaaig % dacaaIWaaaaa!59A9! f'\left( b \right) = 8b - \frac{{8000}}{{{b^2}}} \Rightarrow f'\left( b \right) = 0 \Leftrightarrow 8{b^3} - 8000 = 0 \Leftrightarrow b = 10\)

Bảng biến thiên: 

Với \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOyaiabg2 % da9iaaigdacaaIWaGaeyO0H4Taamyyaiabg2da9iaaigdacaaI2aaa % aa!3F1A! b = 10 \Rightarrow a = 16\)

Vậy diện tích đáy hố ga để khi xây hố tiết kiệm được nguyên liệu nhất là:\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4uamaaBa % aaleaacaWGreaabeaakiabg2da9iaaigdacaaI2aGaaiOlaiaaigda % caaIWaGaeyypa0JaaGymaiaaiAdacaaIWaWaaeWaaeaaieaacaWFJb % Gaa8xBamaaCaaaleqabaGaa8NmaaaaaOGaayjkaiaawMcaaaaa!43CA! {S_{đ}} = 16.10 = 160\left( {c{m^2}} \right)\)

(C)  có tâm O( 0;0) và bán kính R =1.

Qua phép đối xứng tâm I ( 1;0), ảnh của O(0;0)  là O'(2;0) (vì I là trung điểm của OO'),  với R' = R là bán kính của (C').

Vậy phương trình đường tròn (C') là: \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaeWaaeaaca % WG4bGaeyOeI0IaaGOmaaGaayjkaiaawMcaamaaCaaaleqabaGaaGOm % aaaakiabgUcaRiaadMhadaahaaWcbeqaaiaaikdaaaGccqGH9aqpca % aIXaaaaa!3FAA! {\left( {x - 2} \right)^2} + {y^2} = 1\)