Đề thi thử tốt nghiệp THPT QG môn Vật Lý năm 2020 - Trường THPT Nguyễn Bá Ngọc
Đề thi thử tốt nghiệp THPT QG môn Vật Lý năm 2020
-
Hocon247
-
40 câu hỏi
-
90 phút
-
70 lượt thi
-
Trung bình
Tham gia [ Hs Hocon247.com ] - Cộng Đồng Luyện Thi Trực Tuyến để được học tập những kiến thức bổ ích từ HocOn247.com
Một dây dẫn thẳng dài đặt trong không khí có dòng điện với cường độ I chạy qua. Độ lớn cảm ứng từ B do dòng điện này gây ra tại một điểm cách dây một đoạn r được tính bởi công thức
Độ lớn cảm ứng từ B do dòng điện này gây ra tại một điểm cách dây một đoạn r là:
\(B = {2.10^{ - 7}}\frac{I}{r}\)
Trong một điện trường đều có cường độ E, khi một điện tích dương q di chuyển cùng chiều đường sức điện một đoạn d thì công của lực điện là
Công của lực điện làm một điện tích dương q di chuyển cùng chiều đường sức điện một đoạn d:
A = qEd
Một khung dây dẫn tròn, phẳng, bán kính 10 cm gồm 50 vòng dây được đặt trong từ trường đều. Cảm ứng từ hợp với mặt phẳng khung một góc 600. Lúc đầu cảm ứng từ có giá trị bằng 50 mT. Trong khoảng thời gian 50 ms, nếu cảm ứng từ tăng đều lên gấp đôi thì độ lớn suất điện động cảm ứng trong khung là e1, còn nếu cảm ứng từ giảm đều đến không thì độ lớn suất điện động cảm ứng trong khung là e2. Khi đó tổng e1 + e2 bằng
Góc hợp bởi cảm ứng từ và vecto pháp tuyến của mặt phẳng khung dây là:
\(\alpha = 90^\circ - 60^\circ = 30^\circ \)
Cảm ứng từ tăng lên gấp đôi, độ lớn suất điện động cảm ứng trong khung là:
\(\begin{array}{l} {e_1} = \left| { - N\frac{{\Delta B.S\cos \alpha }}{{\Delta t}}} \right| = \left| {\frac{{\left( {2B - B} \right).\pi {R^2}\cos \alpha }}{{\Delta t}}} \right|\\ \Rightarrow {e_1} = \left| { - 50.\frac{{\left( {{{2.50.10}^{ - 3}} - {{50.10}^{ - 3}}} \right).\pi .0,{1^2}.cos{{30}^0}}}{{{{50.10}^{ - 3}}}}} \right| = 1,36{\mkern 1mu} {\mkern 1mu} \left( V \right) \end{array}\)
Cảm ứng từ giảm đều đến 0, độ lớn suất diện động cảm ứng trong khung là:
\(\begin{array}{l} \Rightarrow {e_2} = \left| { - N\frac{{\Delta {B_2}.S.cos\alpha }}{{\Delta t}}} \right| = \left| { - N\frac{{\left( {0 - B} \right).\pi {R^2}.cos\alpha }}{{\Delta t}}} \right|\\ {e_2} = \left| { - 50.\frac{{\left( {0 - {{50.10}^{ - 3}}} \right).\pi .0,{1^2}.cos{{30}^0}}}{{{{50.10}^{ - 3}}}}} \right| = 1,36{\mkern 1mu} {\mkern 1mu} \left( V \right)\\ \Rightarrow {e_1} + {e_2} = 1,36 + 1,36 = 2,72{\mkern 1mu} {\mkern 1mu} \left( V \right) \end{array}\)
Cho mạch điện một chiều gồm nguồn điện có suất điện động E = 12 V, điện trở trong \(r = 1{\mkern 1mu} {\mkern 1mu} \Omega \), mạch ngoài gồm điện trở \({R_0} = 3{\mkern 1mu} {\mkern 1mu} \Omega \) mắc nối tiếp với một biến trở RV. Điều chỉnh biến trở để công suất tiêu thụ trên biến trở đạt giá trị cực đại. Giá trị cực đại đó bằng
Cường độ dòng điện trong mạch là:
\(I = \frac{E}{{{R_V} + {R_0} + r}}\)
Công suất tiêu thụ trên biến trở là:
\({P_V} = {I^2}{R_V} = \frac{{{E^2}{R_V}}}{{{{\left( {{R_V} + {R_0} + r} \right)}^2}}} = \frac{{{E^2}}}{{{R_V} + \frac{{{{\left( {{R_0} + r} \right)}^2}}}{{{R_V}}} + 2\left( {{R_0} + r} \right)}}\)
Để công suất tiêu thụ trên biến trở đạt cực đại:
\(\begin{array}{l} {P_{V\max }} \Leftrightarrow {\left[ {{R_V} + \frac{{{{\left( {{R_0} + r} \right)}^2}}}{{{R_V}}} + 2\left( {{R_0} + r} \right)} \right]_{\min }}\\ \Leftrightarrow {\left[ {{R_V} + \frac{{{{\left( {{R_0} + r} \right)}^2}}}{{{R_V}}}} \right]_{\min }} \end{array}\)
Áp dụng bất đẳng thức Cô-si, ta có:
\({R_V} + \frac{{{{\left( {{R_0} + r} \right)}^2}}}{{{R_V}}} \ge 2\left( {{R_0} + r} \right)\)
(dấu “=” xảy ra \( \Leftrightarrow {R_V} = \frac{{{{\left( {{R_0} + r} \right)}^2}}}{{{R_V}}} \Leftrightarrow {R_V} = {R_0} + r = 3 + 1 = 4{\mkern 1mu} {\mkern 1mu} \Omega \) )
Công suất cực đại trên biến trở là:
\({P_{\max }} = \frac{{{E^2}}}{{4\left( {{R_0} + r} \right)}} = \frac{{{{12}^2}}}{{4.\left( {3 + 1} \right)}} = 9{\mkern 1mu} {\mkern 1mu} \left( W \right)\)
Khi nói về dao động cơ cưỡng bức, phát biểu nào sau đây là sai?
Tần số góc của dao động cưỡng bức bằng tần số góc của ngoại lực. Vậy chu kì của dao động cưỡng bức bằng chu kì của lực cưỡng bức. → A đúng.
Biên độ của dao động cưỡng bức tỉ lệ thuận với biên độ của ngoại lực và phụ thuộc vào tần số góc của ngoại lực. → B, D đúng.
Biên độ cảu dao động cưỡng bức đạt giá trị cực đại khi tần số góc của ngoại lực bằng tần số góc riêng của hệ dao động, khi đó xảy ra hiện tượng cộng hưởng. → C sai.
Một vật dao động điều hòa theo phương trình \(x = A\cos \left( {\omega t + \varphi } \right)\). Tần số góc của dao động là
Phương trình dao động điều hòa: \(x = A\cos \left( {\omega t + \varphi } \right)\),
trong đó x là li độ; A là biên độ dao động;
w là tần số góc;
φ là pha ban đầu;
(ωt + φ) là pha dao động
Hai dao động có phương trình lần lượt là: \({x_1} = 5\cos \left( {2\pi t + 0,75\pi } \right){\mkern 1mu} {\mkern 1mu} \left( {cm} \right);{x_2} = 10\cos \left( {2\pi t + 0,5\pi } \right){\mkern 1mu} {\mkern 1mu} \left( {cm} \right)\) . Độ lệch pha của hai dao động này có độ lớn bằng
Độ lệch pha của hai dao động này là:
\(\Delta \varphi = \left| {{\varphi _1} - {\varphi _2}} \right| = \left| {0,75\pi - 0,5\pi } \right| = 0,25\pi {\mkern 1mu} {\mkern 1mu} \left( {rad} \right)\)
Một vật nhỏ khối lượng 100 g dao động theo phương trình x = 8cos 10t (x tính bằng cm, t tính bằng s). Động năng cực đại của vật bằng
Động năng cực đại của vật là:
\({W_{d\max }} = \frac{1}{2}m{\omega ^2}{A^2} = \frac{1}{2}.0,{1.10^2}.0,{08^2} = 0,032{\mkern 1mu} {\mkern 1mu} \left( J \right) = 32{\mkern 1mu} {\mkern 1mu} \left( {mJ} \right)\)
Một chất điểm dao động điều hòa có vận tốc cực đại 60 cm/s và gia tốc cực đại là 2π m/s2. Chọn mốc thế năng tại vị trí cân bằng. Thời điểm ban đầu (t = 0), chất điểm có vận tốc 30 cm/s và thế năng đang tăng. Chất điểm có gia tốc bằng π m/s2 lần đầu tiên ở thời điểm
Ta có vận tốc cực đại và gia tốc cực đại của vật:
\(\left\{ {\begin{array}{*{20}{l}} {{v_{\max }} = \omega A = 60}\\ {{a_{\max }} = {\omega ^2}A = 200\pi } \end{array}} \right. \Rightarrow \left\{ {\begin{array}{*{20}{l}} {A = \frac{{18}}{\pi }{\mkern 1mu} {\mkern 1mu} \left( {cm} \right)}\\ {\omega = \frac{{10\pi }}{3}{\mkern 1mu} {\mkern 1mu} \left( {rad/s} \right)} \end{array}} \right.\)
Tại thời điểm ban đầu t = 0, vật có vận tốc v > 0 và thế năng đang tăng, vật chuyển động đến biên, ta có:
\(\begin{array}{l} {x_0}^2 + \frac{{{v_0}^2}}{{{\omega ^2}}} = {A^2} \Rightarrow {x_0}^2 + \frac{{{{30}^2}}}{{{{\left( {\frac{{10\pi }}{3}} \right)}^2}}} = {\left( {\frac{{18}}{\pi }} \right)^2}\\ \Rightarrow {x_0} = \pm \frac{{18\sqrt 3 }}{{2\pi }}{\mkern 1mu} {\mkern 1mu} \left( {cm} \right) = \pm A\frac{{\sqrt 3 }}{2} \end{array}\)
Ở thời điểm chất điểm có gia tốc 100π cm/s2 lần đầu tiên, ta có:
\(\begin{array}{l} a = - {\omega ^2}x \Rightarrow 100\pi = - {\left( {\frac{{10\pi }}{3}} \right)^2}x\\ \Rightarrow x = - \frac{9}{\pi }{\mkern 1mu} {\mkern 1mu} \left( {cm} \right) = - \frac{A}{2} \end{array}\)
Ta có vòng tròn lượng giác:
Từ vòng tròn lượng giác, ta thấy tại thời điểm vật có gia tốc 100π cm/s2 lần đầu tiên, vecto quay được góc \(\frac{{5\pi }}{6}{\mkern 1mu} {\mkern 1mu} rad\)
Thời điểm vật có gia tốc 100π cm/s2 lần đầu tiên là:
\(\Delta t = \frac{{\Delta \varphi }}{\omega } = \frac{{\frac{{5\pi }}{6}}}{{\frac{{10\pi }}{3}}} = 0,25{\mkern 1mu} {\mkern 1mu} \left( s \right)\)
Con lắc lò xo dọc gồm lò xo có độ cứng k, đầu trên cố định, đầu dưới có treo vật m. Khi con lắc ở vị trí cân bằng thì lò xo giãn một đoạn 4 cm. Cho con lắc dao động theo phương thẳng đứng. Bỏ qua ma sát, lấy π2 = 10, lấy g = 10 m/s2. Con lắc dao động với chu kì bằng
Chu kì dao động của con lắc là:
\(T = 2\pi \sqrt {\frac{{\Delta {\rm{l}}}}{g}} = 2.\sqrt {10} .\sqrt {\frac{{0,04}}{{10}}} = 0,4{\mkern 1mu} {\mkern 1mu} \left( s \right)\)
Một thấu kính hội tụ có tiêu cự 15 cm. M là một điểm nằm trên trục chính của thấu kính, P là một chất điểm dao động điều hòa quanh vị trí cân bằng trùng với điểm M. Gọi P’ là ảnh của P qua thấu kính. Khi P dao động theo phương vuông góc với trục chính, biên độ 5 cm thì P’ là ảnh ảo dao động với biên độ 10 cm. Nếu P dao động dọc theo trục chính với tần số 5 Hz, biên độ 2,5 cm thì P’ có tốc độ trung bình trong khoảng thời gian 0,2 s bằng
Khi P dao động theo phương vuông góc với trục chính của thấu kính, độ phóng đại của ảnh là:
\(k = - \frac{{d'}}{d} = - 2 \Rightarrow d' = - 2d\)
Ta có công thức thấu kính:
\(\begin{array}{l} \frac{1}{d} + \frac{1}{{d'}} = \frac{1}{f} \Rightarrow \frac{1}{d} + \frac{1}{{ - 2d}} = \frac{1}{{15}}\\ \Rightarrow d = 7,5{\mkern 1mu} {\mkern 1mu} \left( {cm} \right) \end{array}\)
Khi P dao động theo phương trục chính, khoảng cách cực đại và cực tiểu của P tới quang tâm là:
\(\left\{ {\begin{array}{*{20}{l}} {{d_{\max }} = 7,5 + 2,5 = 10{\mkern 1mu} {\mkern 1mu} \left( {cm} \right)}\\ {{d_{\min }} = 7,5 - 2,5 = 5{\mkern 1mu} {\mkern 1mu} \left( {cm} \right)} \end{array}} \right.\)
Ta có công thức thấu kính:
\(\begin{array}{l} \left\{ \begin{array}{l} \frac{1}{{{d_{\max }}}} + \frac{1}{{{{d'}_{\min }}}} = \frac{1}{f}\\ \frac{1}{{{d_{\min }}}} + \frac{1}{{{{d'}_{\max }}}} = \frac{1}{f} \end{array} \right. \Rightarrow \left\{ \begin{array}{l} \frac{1}{{10}} + \frac{1}{{{{d'}_{\min }}}} = \frac{1}{{15}}\\ \frac{1}{5} + \frac{1}{{{{d'}_{\max }}}} = \frac{1}{{15}} \end{array} \right.\\ \Rightarrow \left\{ \begin{array}{l} {{d'}_{\min }} = - 30\left( {cm} \right)\\ {{d'}_{\max }} = - 7,5\left( {cm} \right) \end{array} \right. \end{array}\)
Chiều dài quỹ đạo của ảnh P’ là:
\(L = \left| {{{d'}_{\max }} - {{d'}_{\min }}} \right| = \left| { - 7,5 - \left( { - 30} \right)} \right| = 22,5\left( {cm} \right)\)
Chu kì dao động của chất điểm P là:
\(T = \frac{1}{f} = \frac{1}{5} = 0,2\,\left( s \right)\)
Vậy ảnh P’ dao động với chu kì T' = 0,2s
Tốc độ trung bình của ảnh P’ trong 1 chu kì là:
\({v_{tb}} = \frac{{2L}}{{T'}} = \frac{{2.22,5}}{{0,2}} = 225{\mkern 1mu} {\mkern 1mu} \left( {cm/s} \right) = 2,25{\mkern 1mu} {\mkern 1mu} \left( {m/s} \right)\)
Một sóng cơ hình sin truyền theo trục Ox với chu kì T. Khoảng thời gian để sóng truyền được quãng đường bằng một bước sóng là
Để sóng truyền được quãng đường bằng một bước sóng, khoảng thời gian sóng truyền là T.
Một sóng cơ truyền dọc theo trục Ox. Phương trình dao động của phần tử tại một điểm trên phương truyền sóng là \(u = 4\cos \left( {20\pi t} \right)\) (u tính bằng mm; t tính bằng s). Biết tốc độ truyền sóng bằng 60 cm/s. Bước sóng của sóng này là
Bước sóng của sóng này là:
\(\lambda = \frac{{v.2\pi }}{\omega } = \frac{{60.2\pi }}{{20\pi }} = 6{\mkern 1mu} {\mkern 1mu} \left( {cm} \right)\)
Trong thí nghiệm giao thoa sóng ở mặt nước, hai nguồn kết hợp đặt tại hai điểm A và B dao động cùng pha theo phương thẳng đứng. Trên đoạn thẳng AB, khoảng cách giữa hai cực tiểu giao thoa liên tiếp là 0,5 cm. Sóng truyền trên mặt nước có bước sóng là
Trên đoạn thẳng AB, khoảng cách giữa hai cực tiêu giao thoa liên tiếp là:
\(\frac{\lambda }{2} = 0,5 \Rightarrow \lambda = 1{\mkern 1mu} {\mkern 1mu} \left( {cm} \right)\)
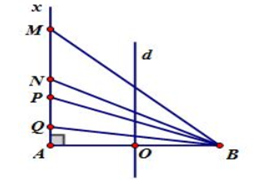
Ở mặt chất lỏng có hai nguồn kết hợp đặt tại A và B dao động điều hòa, cùng pha theo phương thẳng đứng. Ax là nửa đường thẳng nằm ở mặt chất lỏng và vuông góc với AB. Trên Ax có những điểm mà các phần tử ở đó dao động với biên độ cực đại, trong đó M là điểm xa A nhất, N là điểm kế tiếp với M, P là điểm kế tiếp với N và Q là điểm gần A nhất. Biết MN = 22,25 cm; NP = 8,75 cm. Độ dài đoạn QA gần nhất với giá trị nào sau đây?
M, N, P là ba điểm có biên độ cực đại có k = 1; k = 2 và k = 3.
Q là điểm có biên độ cực đại gần A nhất nên Q thuộc vân cực đại có k lớn nhất.
Ta có:
\(\left\{ {\begin{array}{*{20}{l}} {MB - MA = \lambda {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( * \right)}\\ {NB - NA = 2\lambda {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( {**} \right)}\\ {PB - PA = 3\lambda {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( {***} \right)}\\ {QB - QA = k\lambda } \end{array}} \right.\)
Đặt AB = d ta có:
\(\left\{ {\begin{array}{*{20}{l}} {M{B^2} - M{A^2} = {d^2} \Leftrightarrow \left( {MB - MA} \right)\left( {MB + MA} \right) = {d^2} \Rightarrow MB + MA = \frac{{{d^2}}}{\lambda }{\mkern 1mu} {\mkern 1mu} \left( 1 \right)}\\ {N{B^2} - N{A^2} = {d^2} \Leftrightarrow \left( {NB - NA} \right)\left( {NB + NA} \right) = {d^2} \Rightarrow NB + NA = \frac{{{d^2}}}{{2\lambda }}{\mkern 1mu} {\mkern 1mu} \left( 2 \right)}\\ {P{B^2} - P{A^2} = {d^2} \Leftrightarrow \left( {PB - PA} \right)\left( {PB + PA} \right) = {d^2} \Rightarrow PB + PA = \frac{{{d^2}}}{{3\lambda }}{\mkern 1mu} {\mkern 1mu} \left( 3 \right)} \end{array}} \right.\)
Từ (*) và (1) \( \Rightarrow MA = \frac{{{d^2}}}{{2\lambda }} - \frac{\lambda }{2}{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( 4 \right)\)
Từ (**) và (2) \(\Rightarrow NA = \frac{{{d^2}}}{{4\lambda }} - \lambda {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( 5 \right)\)
Từ (***) và (3) \( \Rightarrow PA = \frac{{{d^2}}}{{6\lambda }} - \frac{{3\lambda }}{2}{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( 6 \right)\)
Có : \(MN = MA - NA = 22,25cm\)
Kết hợp (4) và (5) ta được : \(\frac{{{d^2}}}{{2\lambda }} + \lambda = 44,5{\mkern 1mu} {\mkern 1mu} \left( 7 \right)\)
Lại có : NP = NA - PA = 8,75cm
Kết hợp (5) và (6) ta được : \(\frac{{{d^2}}}{{6\lambda }} + \lambda = 17,5{\mkern 1mu} {\mkern 1mu} \left( 8 \right)\)
Giải hệ (7) và (8) được :
\(\left\{ {\begin{array}{*{20}{l}} {d = 18cm}\\ {\lambda = 4cm} \end{array}} \right.\)
Do hai nguồn cùng pha nên :
\(\begin{array}{l} - \frac{d}{\lambda } < k < \frac{d}{\lambda } \Leftrightarrow - 4,5 < k < 4,5\\ \Rightarrow {k_{\max }} = 4 \end{array}\)
Vây điểm Q thuộc đường cực đại ứng với k = 4.
Ta lại có hệ:
\(\begin{array}{l} \left\{ {\begin{array}{*{20}{l}} {QB - QA = 4\lambda }\\ {QB + QA = \frac{{{d^2}}}{{4\lambda }}} \end{array}} \right.\\ \Rightarrow QA = \frac{{{d^2}}}{{8\lambda }} - 2\lambda = \frac{{{{18}^2}}}{{8.4}} - 2.4 = 2,125cm \end{array}\)
Theo thứ tự tăng dần về tần số của các sóng vô tuyến, sắp xếp nào sau đây đúng?
Thứ tự tăng dần về tần số của các sóng vô tuyến: sóng dài, sóng trung, sóng ngắn, sóng cực ngắn.
Từ Trái Đất, các nhà khoa học điều khiển các xe tự hành trên Mặt Trăng nhờ các thiết bị thu phát sóng vô tuyến. Sóng vô tuyến được dùng trong ứng dụng này thuộc dải
Sóng vô tuyến được dùng trong thiết bị thu phát sóng vô tuyến để điều khiển xe tự hành trên Mặt Trăng là sóng cực ngắn.
Hai mạch dao động điện từ lí tưởng đang có dao động điện từ tự do với cùng cường độ dòng điện cực đại I0. Chu kì dao động riêng của mạch thứ nhất là T1, của mạch thứ hai là T2 = 2T1. Khi cường độ dòng điện trong hai mạch có cùng độ lớn và nhỏ hơn I0 thì độ lớn điện tích trên một bản tụ điện của mạch dao động thứ nhất là q1 và của mạch dao động thứ hai là q2. Tỉ số \(\frac{{{q_1}}}{{{q_2}}}\) là
Theo đề bài ta có: \(% MathType!MTEF!2!1!+- % faaahqart1ev3aaaKnaaaaWenf2ys9wBH5garuavP1wzZbItLDhis9 % wBH5garmWu51MyVXgaruWqVvNCPvMCG4uz3bqee0evGueE0jxyaiba % ieYlf9irVeeu0dXdh9vqqj-hHeeu0xXdbba9frFj0-OqFfea0dXdd9 % vqaq-JfrVkFHe9pgea0dXdar-Jb9hs0dXdbPYxe9vr0-vr0-vqpi0d % c9GqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaabaaaaaaaaape % Gaamiva8aadaWgaaWcbaWdbiaaikdaa8aabeaak8qacqGH9aqpcaaI % YaGaamiva8aadaWgaaWcbaWdbiaaigdaa8aabeaak8qacqGHshI3ca % WGrbWdamaaBaaaleaapeGaaGimaiaaikdaa8aabeaak8qacqGH9aqp % caaIYaGaamyua8aadaWgaaWcbaWdbiaaicdacaaIXaaapaqabaaaaa!4240! {T_2} = 2{T_1} \Rightarrow {Q_{02}} = 2{Q_{01}}\)
Áp dụng công thức độc lập với thời gian cho hai mạch, ta có
\( \left\{ {\begin{array}{*{20}{l}} {\frac{{{i^2}}}{{{I_0}^2}} + \frac{{{q_1}^2}}{{{Q_{01}}^2}} = 1}\\ {\frac{{{i^2}}}{{{I_0}^2}} + \frac{{{q_2}^2}}{{{Q_{02}}^2}} = 1} \end{array}} \right. \Rightarrow \frac{{{q_1}^2}}{{{Q_{01}}^2}} = \frac{{{q_2}^2}}{{{Q_{02}}^2}} \Rightarrow \frac{{{q_1}}}{{{q_2}}} = \frac{{{Q_{01}}}}{{{Q_{02}}}} = 0,5\)
Một anten parabol đặt tại điểm M trên mặt đất, phát ra một sóng truyền theo phương làm với mặt phẳng nằm ngang một góc 300 hướng lên cao. Sóng này phản xạ trên tầng điện li, rồi trở lại gặp mặt đất ở điểm N. Xem mặt đất và tầng điện li là những mặt cầu đồng tâm có bán kính lần lượt là R1 = 6400 km và R2 = 6500 km. Bỏ qua sự tự quay của trái đất. Cung MN có độ dài gần giá trị nào nhất sau đây?
Áp dụng định lí hàm sin cho tam giác OMI, ta có:
\(\begin{array}{l} \frac{{OM}}{{\sin \widehat {MIO}}} = \frac{{OI}}{{\sin \widehat {OMI}}}\\ \Rightarrow \frac{{6400}}{{\sin \widehat {MIO}}} = \frac{{6500}}{{\sin \left( {{{90}^0} + {{30}^0}} \right)}}\\ \Rightarrow \sin \widehat {MIO} = 0,823\\ \Rightarrow \widehat {MIO} = 58,{5^0}\\ \Rightarrow \alpha = \widehat {MOI} = {180^0} - \widehat {OMI} - \widehat {MIO}\\ \Leftrightarrow \alpha = {180^0} - \left( {{{90}^0} + {{30}^0}} \right) - 58,{5^0} = 1,{5^0} = 0,026{\mkern 1mu} {\mkern 1mu} \left( {rad} \right) \end{array}\)
Độ dài cung MN là:
\({\rm{l}} = 2\alpha {R_1} = 2.0,026.6400 = 332,8{\mkern 1mu} {\mkern 1mu} \left( {km} \right)\)
Suất điện động \(e = 100\cos \left( {100\pi t + \pi } \right){\mkern 1mu} {\mkern 1mu} \left( V \right)\) có giá trị cực đại là
Biểu thức suất điện động:
\(e = {E_0}\cos \left( {\omega t + \varphi } \right)\)
với e là suất điện động tức thời, E0 là suất điện động cực đại, w là tần số góc, φ là pha ban đầu, (wt + φ) là pha dao động.
=> Suất điện động cực đại là E0 = 100 V
Đặt điện áp \(u = {U_0}.\cos \left( {100\pi t} \right){\mkern 1mu} V\) (với U0 không đổi, ω thay đổi) vào hai đầu đoạn mạch mắc nối tiếp gồm điện trở R, cuộn cảm thuần có độ tự cảm L và tụ điện có điện dung C. Khi \(\omega = {\omega _0}\) thì trong mạch có cộng hưởng điện. Tần số góc \( {\omega _0}\) là:
Điều kiện có cộng hưởng điện:
\({Z_L} = {Z_C} \Leftrightarrow {\omega _0}L = \frac{1}{{{\omega _0}C}} \Rightarrow {\omega _0} = \frac{1}{{\sqrt {LC} }}\)
Đặt vào hai đầu điện trở một điện áp xoay chiều có giá trị hiệu dụng không đổi và tần số f thay đổi được. Khi f = f0 và f = 2f0 thì công suất tiêu thụ của điện trở tương ứng là P1 và P2. Hệ thức nào sau đây đúng?
Ta có công thức xác định công suất tiêu thụ trên điện trở: \(% MathType!MTEF!2!1!+- % faaahqart1ev3aaaKnaaaaWenf2ys9wBH5garuavP1wzZbItLDhis9 % wBH5garmWu51MyVXgaruWqVvNCPvMCG4uz3bqee0evGueE0jxyaiba % ieYlf9irVeeu0dXdh9vqqj-hHeeu0xXdbba9frFj0-OqFfea0dXdd9 % vqaq-JfrVkFHe9pgea0dXdar-Jb9hs0dXdbPYxe9vr0-vr0-vqpi0d % c9GqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaabaaaaaaaaape % Gaamiuaiabg2da9maalaaapaqaa8qacaWGvbWdamaaCaaaleqabaWd % biaaikdaaaaak8aabaWdbiaadkfaaaaaaa!37D5! P = \frac{{{U^2}}}{R}\)Đoạn mạch xoay chiều chỉ có điện trở, công suất tiêu thụ không phụ thuộc vào tần số. Do đó: \(% MathType!MTEF!2!1!+- % faaahqart1ev3aaaKnaaaaWenf2ys9wBH5garuavP1wzZbItLDhis9 % wBH5garmWu51MyVXgaruWqVvNCPvMCG4uz3bqee0evGueE0jxyaiba % ieYlf9irVeeu0dXdh9vqqj-hHeeu0xXdbba9frFj0-OqFfea0dXdd9 % vqaq-JfrVkFHe9pgea0dXdar-Jb9hs0dXdbPYxe9vr0-vr0-vqpi0d % c9GqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaabaaaaaaaaape % Gaamiua8aadaWgaaWcbaWdbiaaikdaa8aabeaak8qacqGH9aqpcaWG {P_2} = {P_1}\)
Đặt điện áp xoay chiều \(% MathType!MTEF!2!1!+- % faaahqart1ev3aaaKnaaaaWenf2ys9wBH5garuavP1wzZbItLDhis9 % wBH5garmWu51MyVXgaruWqVvNCPvMCG4uz3bqee0evGueE0jxyaiba % ieYlf9irVeeu0dXdh9vqqj-hHeeu0xXdbba9frFj0-OqFfea0dXdd9 % vqaq-JfrVkFHe9pgea0dXdar-Jb9hs0dXdbPYxe9vr0-vr0-vqpi0d % c9GqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaabaaaaaaaaape % GaamyDaiabg2da9iaadwfapaWaaSbaaSqaa8qacaaIWaaapaqabaGc % peGaaiOlaiGacogacaGGVbGaai4Camaabmaapaqaa8qacaaIXaGaaG % imaiaaicdacqaHapaCcaWG0baacaGLOaGaayzkaaWdaiaayEW7peGa % amOvaaaa!438D! u = {U_0}.\cos \left( {100\pi t} \right){\mkern 1mu} V\) (t tính bằng s) vào hai đầu một tụ điện có điện dung \(% MathType!MTEF!2!1!+- % faaahqart1ev3aaaKnaaaaWenf2ys9wBH5garuavP1wzZbItLDhis9 % wBH5garmWu51MyVXgaruWqVvNCPvMCG4uz3bqee0evGueE0jxyaiba % ieYlf9irVeeu0dXdh9vqqj-hHeeu0xXdbba9frFj0-OqFfea0dXdd9 % vqaq-JfrVkFHe9pgea0dXdar-Jb9hs0dXdbPYxe9vr0-vr0-vqpi0d % c9GqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaabaaaaaaaaape % WaaSaaa8aabaWdbiaaigdacaaIWaWdamaaCaaaleqabaWdbiabgkHi \frac{{{{10}^{ - 4}}}}{\pi }F\). Dung kháng của tụ là:
Dung kháng của tụ là: \(% MathType!MTEF!2!1!+- % faaahqart1ev3aaaKnaaaaWenf2ys9wBH5garuavP1wzZbItLDhis9 % wBH5garmWu51MyVXgaruWqVvNCPvMCG4uz3bqee0evGueE0jxyaiba % ieYlf9irVeeu0dXdh9vqqj-hHeeu0xXdbba9frFj0-OqFfea0dXdd9 % vqaq-JfrVkFHe9pgea0dXdar-Jb9hs0dXdbPYxe9vr0-vr0-vqpi0d % c9GqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaabaaaaaaaaape % GaamOwa8aadaWgaaWcbaWdbiaadoeaa8aabeaak8qacqGH9aqpdaWc % aaWdaeaapeGaaGymaaWdaeaapeGaeqyYdCNaam4qaaaacqGH9aqpda % WcaaWdaeaapeGaaGymaaWdaeaapeGaaGymaiaaicdacaaIWaGaeqiW % daNaaiOlamaalaaapaqaa8qacaaIXaGaaGima8aadaahaaWcbeqaa8 % qacqGHsislcaaI0aaaaaGcpaqaa8qacqaHapaCaaaaaiabg2da9iaa % igdacaaIWaGaaGimaiabfM6axbaa!4A99! {Z_C} = \frac{1}{{\omega C}} = \frac{1}{{100\pi .\frac{{{{10}^{ - 4}}}}{\pi }}} = 100\Omega \)
Đặt điện áp \(% MathType!MTEF!2!1!+- % faaahqart1ev3aaaKnaaaaWenf2ys9wBH5garuavP1wzZbItLDhis9 % wBH5garmWu51MyVXgaruWqVvNCPvMCG4uz3bqee0evGueE0jxyaiba % ieYlf9irVeeu0dXdh9vqqj-hHeeu0xXdbba9frFj0-OqFfea0dXdd9 % vqaq-JfrVkFHe9pgea0dXdar-Jb9hs0dXdbPYxe9vr0-vr0-vqpi0d % c9GqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaabaaaaaaaaape % GaamyDaiabg2da9iaaikdacaaIWaGaaGimamaakaaapaqaa8qacaaI % YaaaleqaaOGaaiOlaiGacogacaGGVbGaai4Camaabmaapaqaa8qaca % aIXaGaaGimaiaaicdacqaHapaCcaWG0baacaGLOaGaayzkaaWdaiaa % yEW7peGaamOvaaaa!44B5! u = 200\sqrt 2 .\cos \left( {100\pi t} \right){\mkern 1mu} V\) vào hai đầu một điện trở thuần . Công suất tiêu thụ của điện trở bằng:
Công suất tiêu thụ của điện trở: \(% MathType!MTEF!2!1!+- % faaahqart1ev3aaaKnaaaaWenf2ys9wBH5garuavP1wzZbItLDhis9 % wBH5garmWu51MyVXgaruWqVvNCPvMCG4uz3bqee0evGueE0jxyaiba % ieYlf9irVeeu0dXdh9vqqj-hHeeu0xXdbba9frFj0-OqFfea0dXdd9 % vqaq-JfrVkFHe9pgea0dXdar-Jb9hs0dXdbPYxe9vr0-vr0-vqpi0d % c9GqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaabaaaaaaaaape % Gaamiuaiabg2da9maalaaapaqaa8qacaWGvbWdamaaCaaaleqabaWd % biaaikdaaaaak8aabaWdbiaadkfaaaGaeyypa0ZaaSaaa8aabaWdbi % aaikdacaaIWaGaaGima8aadaahaaWcbeqaa8qacaaIYaaaaaGcpaqa % a8qacaaIXaGaaGimaiaaicdaaaGaeyypa0JaaGinaiaaicdacaaIWa P = \frac{{{U^2}}}{R} = \frac{{{{200}^2}}}{{100}} = 400W\)
Cho đoạn mạch xoay chiều gồm cuộn dây không thuần cảm (R, L) mắc nối tiếp với tụ điện C, thoả mãn \(% MathType!MTEF!2!1!+- % faaahqart1ev3aaaKnaaaaWenf2ys9wBH5garuavP1wzZbItLDhis9 % wBH5garmWu51MyVXgaruWqVvNCPvMCG4uz3bqee0evGueE0jxyaiba % ieYlf9irVeeu0dXdh9vqqj-hHeeu0xXdbba9frFj0-OqFfea0dXdd9 % vqaq-JfrVkFHe9pgea0dXdar-Jb9hs0dXdbPYxe9vr0-vr0-vqpi0d % c9GqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaabaaaaaaaaape % GaaGOmaiaadYeacqGH+aGpcaWGdbGaamOua8aadaahaaWcbeqaa8qa 2L > C{R^2}\) . Đặt vào hai đầu đoạn mạch một điện áp xoay chiều \(% MathType!MTEF!2!1!+- % faaahqart1ev3aaaKnaaaaWenf2ys9wBH5garuavP1wzZbItLDhis9 % wBH5garmWu51MyVXgaruWqVvNCPvMCG4uz3bqee0evGueE0jxyaiba % ieYlf9irVeeu0dXdh9vqqj-hHeeu0xXdbba9frFj0-OqFfea0dXdd9 % vqaq-JfrVkFHe9pgea0dXdar-Jb9hs0dXdbPYxe9vr0-vr0-vqpi0d % c9GqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaabaaaaaaaaape % GaamyDaiabg2da9iaadwfapaWaaSbaaSqaa8qacaaIWaaapaqabaGc % peGaaiOlaiGacogacaGGVbGaai4Camaabmaapaqaa8qacqaHjpWDca u = {U_0}.\cos \left( {\omega t} \right)\) (với U0 không đổi, ω thay đổi). Điều chỉnh ω để điện áp hiệu dụng giữa hai đầu tụ điện đạt giá trị cực đại, khi đó hiệu điện thế giữa hai đầu cuộn dây sớm pha hơn hiệu điện thế giữa hai đầu đoạn mạch một góc φ. Giá trị nhỏ nhất mà φ có thể đạt được là:
\(% MathType!Translator!2!1!LaTeX.tdl!LaTeX 2.09 and later! % MathType!MTEF!2!1!+- % faaahqart1ev3aaaKnaaaaWenf2ys9wBH5garuavP1wzZbItLDhis9 % wBH5garmWu51MyVXgaruWqVvNCPvMCaebbnrfifHhDYfgasaacH8sr % ps0lbbf9q8WrFfeuY-ribbf9v8qqaqFr0xc9pk0xbba9q8WqFfea0- % yr0RYxir-Jbba9q8aq0-yq-He9q8qqQ8frFve9Fve9Ff0dc9Gqpi0d % meaabaqaciGacaGaaeqabaWaaeaaeaaakeaaciGG0bGaaiyyaiaac6 % gacqaHXoqycqGH9aqpciGG0bGaaiyyaiaac6gacaGGOaGaeqOXdO2a % aSbaaSqaaiaadkfacaWGmbaabeaakiabgkHiTiabeA8aQnaaBaaale % aacaWGsbGaamitaiaadoeaaeqaaOGaaiykaiabg2da9maalaaabaGa % amiEaiabgkHiTiaadMhaaeaacaaIXaGaey4kaSIaamiEaiaadMhaaa % aaaa!4BA0! \tan \alpha = \tan ({\varphi _{RL}} - {\varphi _{RLC}}) = \frac{{x - y}}{{1 + xy}}\)
Với \(% MathType!Translator!2!1!LaTeX.tdl!LaTeX 2.09 and later! % MathType!MTEF!2!1!+- % faaahqart1ev3aaaKnaaaaWenf2ys9wBH5garuavP1wzZbItLDhis9 % wBH5garmWu51MyVXgaruWqVvNCPvMCaebbnrfifHhDYfgasaacH8sr % ps0lbbf9q8WrFfeuY-ribbf9v8qqaqFr0xc9pk0xbba9q8WqFfea0- % yr0RYxir-Jbba9q8aq0-yq-He9q8qqQ8frFve9Fve9Ff0dc9Gqpi0d % meaabaqaciGacaGaaeqabaWaaeaaeaaakeaacaWG4bGaeyypa0Jaci % iDaiaacggacaGGUbGaeqOXdO2aaSbaaSqaaiaadkfacaWGmbaabeaa % kiaacYcacaWG5bGaeyypa0JaciiDaiaacggacaGGUbGaeqOXdO2aaS % baaSqaaiaadkfacaWGmbGaam4qaaqabaaaaa!43CC! x = \tan {\varphi _{RL}},y = \tan {\varphi _{RLC}} \), ta có \(% MathType!MTEF!2!1!+- % faaahqart1ev3aaaKnaaaaWenf2ys9wBH5garuavP1wzZbItLDhis9 % wBH5garmWu51MyVXgaruWqVvNCPvMCaebbnrfifHhDYfgasaacH8sr % ps0lbbf9q8WrFfeuY-ribbf9v8qqaqFr0xc9pk0xbba9q8WqFfea0- % yr0RYxir-Jbba9q8aq0-yq-He9q8qqQ8frFve9Fve9Ff0dc9Gqpi0d % meaabaqaciGacaGaaeqabaWaaeaaeaaakeaacaWG4bGaamyEaiabg2 % da9iabgkHiTmaalaaabaGaaGymaaqaaiaaikdaaaaaaa!36F4! xy = - \frac{1}{2}\)
\(% MathType!MTEF!2!1!+- % faaahqart1ev3aaaKnaaaaWenf2ys9wBH5garuavP1wzZbItLDhis9 % wBH5garmWu51MyVXgaruWqVvNCPvMCaebbnrfifHhDYfgasaacH8sr % ps0lbbf9q8WrFfeuY-ribbf9v8qqaqFr0xc9pk0xbba9q8WqFfea0- % yr0RYxir-Jbba9q8aq0-yq-He9q8qqQ8frFve9Fve9Ff0dc9Gqpi0d % meaabaqaciGacaGaaeqabaWaaeaaeaaakeaacqGHshI3ciGG0bGaai % yyaiaac6gacqaHXoqycqGH9aqpcaaIYaWaaeWaaeaacaWG4bGaey4k % aSYaaSaaaeaacaaIXaaabaGaaGOmaiaadIhaaaaacaGLOaGaayzkaa % GaeyyzImRaaGOmaiaacYcacaaIYaWaaOaaaeaacaWG4bGaaiOlamaa % laaabaGaaGymaaqaaiaaikdacaWG4baaaaWcbeaakiabg2da9iaaik % dadaGcaaqaaiaaikdaaSqabaGccqGHshI3cqaHXoqycqGHLjYScaaI \Rightarrow \tan \alpha = 2\left( {x + \frac{1}{{2x}}} \right) \ge 2,2\sqrt {x.\frac{1}{{2x}}} = 2\sqrt 2 \Rightarrow \alpha \ge 1,23rad\)
Cho bốn ánh sáng đơn sắc: đỏ, tím, cam và lục. Chiết suất của thuỷ tinh có giá trị lớn nhất đối với ánh sáng:
Chiết suất của các chất trong suốt biến thiên theo màu sắc của ánh sáng và tăng dần từ màu đỏ, đến màu tím: \(% MathType!MTEF!2!1!+- % faaahqart1ev3aaaKnaaaaWenf2ys9wBH5garuavP1wzZbItLDhis9 % wBH5garmWu51MyVXgaruWqVvNCPvMCG4uz3bqee0evGueE0jxyaiba % ieYlf9irVeeu0dXdh9vqqj-hHeeu0xXdbba9frFj0-OqFfea0dXdd9 % vqaq-JfrVkFHe9pgea0dXdar-Jb9hs0dXdbPYxe9vr0-vr0-vqpi0d % c9GqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaabaaaaaaaaape % GaamOBa8aadaWgaaWcbaWdbiaadsgaa8aabeaak8qacqGH8aapcaWG % UbWdamaaBaaaleaapeGaamizaiaadogaa8aabeaak8qacqGH8aapca % WGUbWdamaaBaaaleaapeGaamODaaWdaeqaaOWdbiabgYda8iaad6ga % paWaaSbaaSqaa8qacaWGSbGaamyDaiaadogaa8aabeaak8qacqGH8a % apcaGGUaGaaiOlaiaac6cacaGGUaGaeyipaWJaamOBa8aadaWgaaWc % baWdbiaadogacaWGObGaamyyaiaad2gaa8aabeaak8qacqGH8aapca % WGUbWdamaaBaaaleaapeGaamiDaiaadMgacaWGTbaapaqabaaaaa!5127! {n_d} < {n_{dc}} < {n_v} < {n_{luc}} < .... < {n_{cham}} < {n_{tim}}\)
Trong 4 ánh sáng đơn sắc đỏ, tím, cam và lục. Chiết suất của thuỷ tinh có giá trị lớn nhất đối với ánh sáng tím.
Sự phát sáng nào sau đây là hiện tượng quang – phát quang?
Lý thuyết: Hiện tượng quang phát quang là sự hấp thụ ánh sáng có bước sóng này để phát ra ánh sáng có bước sóng khác.
Sự phát sáng của đèn ống thông dụng là hiện tượng quang – phát quang.
Thành trong của các đèn ống thông dụng có phủ một lớp bột phát quang. Lớp bột này sẽ phát quang ánh sáng trắng khi bị kích thích bởi ánh sáng giàu tia tử ngoại do hơi thuỷ ngân trong đèn phát ra lúc có sự phóng điện qua nó.
Khi nói về tia hồng ngoại và tia tử ngoại, phát biểu nào sau đây là đúng?
Thang sóng điện từ:
.png)
Ta có: Tia hồng ngoại có bước sóng lớn hơn bước sóng của ánh sáng đỏ, tia tử ngoại có bước sóng nhỏ hơn bước sóng của ánh sáng tím.
Vậy bước sóng của tia hồng ngoại lớn hơn bước sóng của tia tử ngoại.
Từ không khí, chiếu chùm sáng hẹp (coi như một tia sáng) gồm hai bức xạ đơn sắc màu đỏ và màu tím tới mặt nước với góc tới 530 thì xảy ra hiện tượng phản xạ và khúc xạ. Biết tia khúc xạ màu đỏ vuông góc với tia phản xạ, góc giữa tia khúc xạ màu tím và tia khúc xạ màu đỏ là 0,50. Chiết suất của nước đối với tia sáng màu tím là:
Ta có: \(\left\{ {\begin{array}{*{20}{l}} {n = \frac{c}{v} = \frac{{cT}}{\lambda } \Rightarrow n \sim \frac{1}{\lambda }}\\ {{\lambda _d} > {\lambda _t}} \end{array}} \right. \Rightarrow {n_d} < {n_t}\)
Lại có: \(% MathType!MTEF!2!1!+- % faaahqart1ev3aaaKnaaaaWenf2ys9wBH5garuavP1wzZbItLDhis9 \left\{ {\begin{array}{*{20}{l}} {\sin i = n.\sin {\mkern 1mu} r \Rightarrow \frac{{\sin i}}{{\sin {\mkern 1mu} r}} = n}\\ {{n_d} < {n_t}} \end{array}} \right. \Rightarrow {r_d} > {r_t}\)
Áp dụng định luật khúc xạ ánh sáng và dữ kiện tia khúc xạ màu đỏ vuông góc với tia phản xạ ta có: \(\left\{ {\begin{array}{*{20}{l}} {i = i' = {{53}^0}}\\ {{r_d} = 90 - i'} \end{array}} \right. \Rightarrow {r_d} = {37^0}\)
Góc giữa tia khúc xạ màu chàm và tia khúc xạ màu đỏ là 0,50 nên:
\({r_t} = {r_d} - 5 = 37 - 5 = 36,{5^0}\)
\( \Rightarrow {n_t} = \frac{{\sin i}}{{\sin {\mkern 1mu} {r_t}}} = \frac{{\sin 53}}{{\sin 36,5}} = 1,343\)
Trong thí nghiệm giao thoa ánh sáng bằng khe Y – âng, khoảng cách giữa hai khe kết hợp là a = 1mm, khoảng cách từ hai khe đến màn là D = 50cm, ánh sáng sử dụng gồm 4 bức xạ có bước sóng: \(% MathType!MTEF!2!1!+- % faaahqart1ev3aaaKnaaaaWenf2ys9wBH5garuavP1wzZbItLDhis9 % wBH5garmWu51MyVXgaruWqVvNCPvMCG4uz3bqee0evGueE0jxyaiba % ieYlf9irVeeu0dXdh9vqqj-hHeeu0xXdbba9frFj0-OqFfea0dXdd9 % vqaq-JfrVkFHe9pgea0dXdar-Jb9hs0dXdbPYxe9vr0-vr0-vqpi0d % c9GqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaabaaaaaaaaape % Gaeq4UdW2damaaBaaaleaapeGaaGymaaWdaeqaaOWdbiabg2da9iaa % icdacaGGSaGaaGOnaiaaisdacqaH8oqBcaWGTbGaai4oaiabeU7aS9 % aadaWgaaWcbaWdbiaaikdaa8aabeaak8qacqGH9aqpcaaIWaGaaiil % aiaaiAdacqaH8oqBcaWGTbGaai4oaiabeU7aS9aadaWgaaWcbaWdbi % aaiodaa8aabeaak8qacqGH9aqpcaaIWaGaaiilaiaaiwdacaaI0aGa % eqiVd0MaamyBaiaacUdacqaH7oaBpaWaaSbaaSqaa8qacaaI0aaapa % qabaGcpeGaeyypa0JaaGimaiaacYcacaaI0aGaaGioaiabeY7aTjaa % d2gacaGGUaaaaa!5B05! {\lambda _1} = 0,64\mu m;{\lambda _2} = 0,6\mu m;{\lambda _3} = 0,54\mu m;{\lambda _4} = 0,48\mu m.\)
Khoảng cách ngắn nhất giữa hai vân cùng màu với vân trung tâm là:
Vị trí 4 vân sáng trùng nhau:
\(\begin{array}{l} {x_1} = {x_2} = {x_3} = {x_4} \Leftrightarrow {k_1}{\lambda _1} = {k_2}{\lambda _2} = {k_3}{\lambda _3} = {k_4}{\lambda _4}\\ {x_1} = {x_2} = {x_3} = {x_4} \Leftrightarrow {k_1}{\lambda _1} = {k_2}{\lambda _2} = {k_3}{\lambda _3} = {k_4}{\lambda _4}\\ \Leftrightarrow {k_1}.0,64 = {k_2}.0,6 = {k_3}.0,54 = {k_4}.0,48\\ \Leftrightarrow 64{k_1} = 60{k_2} = 54{k_3} = 48{k_4}\\ \Leftrightarrow 32{k_1} = 30{k_2} = 27{k_3} = 24{k_4} \end{array}\)
Ta có: \(BCNN\left( {32;30;27;24} \right) = 4320\)
\(\Rightarrow \left\{ {\begin{array}{*{20}{l}} {{k_1} = \frac{{4320}}{{32}}.n = 135.n}\\ {{k_2} = \frac{{4320}}{{30}}.n = 144.n}\\ {{k_3} = \frac{{4320}}{{27}}.n = 160.n}\\ {{k_4} = \frac{{4320}}{{24}}.n = 180.n} \end{array}} \right.\)
Vị trí vân trùng nhau của 4 bức xạ: \({x_{1234}} = \frac{{{k_1}{\lambda _1}D}}{a} = \frac{{135n.0,64.0,5}}{1} = 43,2.n{\mkern 1mu} \left( {mm} \right) = 4,32.n{\mkern 1mu} {\mkern 1mu} \left( {cm} \right)\)
Khoảng cách ngắn nhất giữa hai vân cùng màu với vân trung tâm là 4,32cm.
Trong thí nghiệm Y – âng về giao thoa ánh sáng, khoảng cách giữa hai khe là 0,5mm, khoảng cách từ mặt phẳng chứa hai khe đến màn quan sát là 2m. Nguồn sáng phát ra vô số ánh sáng đơn sắc có bước sóng biến thiên liên tục từ 380nm đến 750nm. Trên màn, khoảng cách gần nhất từ vân sáng trung tâm đến vị trí mà ở đó có hai bức xạ cho vân sáng là:
Vị trí vân đỏ và vân tím bậc k là: \(% MathType!MTEF!2!1!+- % faaahqart1ev3aaaKnaaaaWenf2ys9wBH5garuavP1wzZbItLDhis9 % wBH5garmWu51MyVXgaruWqVvNCPvMCG4uz3bqee0evGueE0jxyaiba % ieYlf9irVeeu0dXdh9vqqj-hHeeu0xXdbba9frFj0-OqFfea0dXdd9 % vqaq-JfrVkFHe9pgea0dXdar-Jb9hs0dXdbPYxe9vr0-vr0-vqpi0d % c9GqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaabaaaaaaaaape % Waaiqaa8aabaqbamaabiqaaaqaa8qacaWG4bWdamaaBaaaleaapeGa % amizaaWdaeqaaOWdbiabg2da9iaadUgacaGGUaWaaSaaa8aabaWdbi % abeU7aS9aadaWgaaWcbaWdbiaadsgaa8aabeaak8qacaGGUaGaamir % aaWdaeaapeGaamyyaaaacqGH9aqpdaWcaaWdaeaapeGaam4Aaiaac6 % cacaaIWaGaaiilaiaaiEdacaaI1aGaaiOlaiaaikdaa8aabaWdbiaa % icdacaGGSaGaaGynaaaacqGH9aqpcaaIZaGaam4Aa8aacaaMh8+dbm % aabmaapaqaa8qacaWGTbGaamyBaaGaayjkaiaawMcaaaWdaeaapeGa % amiEa8aadaWgaaWcbaWdbiaadshaa8aabeaak8qacqGH9aqpcaWGRb % GaaiOlamaalaaapaqaa8qacqaH7oaBpaWaaSbaaSqaa8qacaWG0baa % paqabaGcpeGaaiOlaiaadseaa8aabaWdbiaadggaaaGaeyypa0ZaaS % aaa8aabaWdbiaadUgacaGGUaGaaGimaiaacYcacaaIZaGaaGioaiaa % c6cacaaIYaaapaqaa8qacaaIWaGaaiilaiaaiwdaaaGaeyypa0JaaG % ymaiaacYcacaaI1aGaaGOmaiaadUgapaGaaG5bV-qadaqadaWdaeaa % peGaamyBaiaad2gaaiaawIcacaGLPaaaaaaacaGL7baaaaa!6EE5! \left\{ {\begin{array}{*{20}{l}} {{x_d} = k.\frac{{{\lambda _d}.D}}{a} = \frac{{k.0,75.2}}{{0,5}} = 3k{\mkern 1mu} \left( {mm} \right)}\\ {{x_t} = k.\frac{{{\lambda _t}.D}}{a} = \frac{{k.0,38.2}}{{0,5}} = 1,52k{\mkern 1mu} \left( {mm} \right)} \end{array}} \right.\)
Ta có bảng sau:
.png)
Dựa vào hình vẽ ta thấy vùng phủ nhau đầu tiên là của hai bậc quang phổ bậc 2 và bậc 3.
Vị trí bắt đầu phủ nhau cách vân sáng trung tâm là 4,56mm (tương ứng với xt3)
Vậy khoảng cách gần nhất từ vân sáng trung tâm đến vị trí mà ở đó có hai bức xạ cho vân sáng là 4,56mm
Pin quang điện (còn gọi là pin Mặt Trời) là nguồn điện chạy bằng năng lượng ánh sáng. Nó biến đổi trực tiếp quang năng thành:
Pin quang điện (còn gọi là pin Mặt Trời) là nguồn điện chạy bằng năng lượng ánh sáng. Nó biến đổi trực tiếp quang năng thành điện năng.
Khi nói về tia laze, phát biểu nào sau đây sai?
Đặc điểm của tia laze: có tính đơn sắc, tịnh định hướng, tính kết hợp cao và cường độ lớn.
Phát biểu không đúng về laze: Tia laze là ánh sáng trắng.
Giới hạn quang điện của một kim loại là 300nm. Lấy \(h = 6,{625.10^{ - 34}}J.s;c = {3.10^8}m/s\). Công thoát electron của kim loại này là:
Công thoát electron của kim loại này là:
\(A = \frac{{hc}}{{{\lambda _0}}} = \frac{{6,{{625.10}^{ - 34}}{{.3.10}^8}}}{{{{300.10}^{ - 9}}}} = 6,{625.10^{ - 19}}J\)
Các mức năng lượng của các trạng thái dừng của nguyên tử hidro được xác định bằng biểu thức \({E_n} = - \frac{{13,6}}{{{n^2}}}eV{\mkern 1mu} {\mkern 1mu} \left( {n = 1,2,3,...} \right)\). Nếu nguyên tử hidro hấp thụ một photon có năng lượng 2,55eV thì bước sóng nhỏ nhất của bức xạ mà nguyên tử hidro có thể phát ra là:
Ta có \({E_n} = - \frac{{13,6}}{{{n^2}}}eV \Rightarrow \left\{ {\begin{array}{*{20}{l}} {{E_{1{\mkern 1mu} }} = - 13,6eV}\\ {{E_{2{\mkern 1mu} }} = - 3,4eV}\\ {{E_{3{\mkern 1mu} }} = - 1,51eV}\\ {{E_{4{\mkern 1mu} }} = - 0,85eV} \end{array}} \right.\)
Thấy rằng : \({E_4}\, - {E_2}\, = - 0,85 + 3,44 = 2,55eV\)
→ Nguyên tử hidro hấp thụ năng lượng 2,55 eV và nhảy từ mức n = 2 lên mức n = 4.
Nguyên tử Hidro có thể phát ra bước sóng nhỏ nhất khi nó chuyển từ mức 4 xuống mức 1.
Ta có:
\({E_4} - {E_1} = \frac{{hc}}{{{\lambda _{41}}}} \Rightarrow {\lambda _{41}} = \frac{{hc}}{{{E_4} - {E_1}}} = \frac{{6,{{625.10}^{ - 34}}{{.3.10}^8}}}{{\left( { - 0,85 + 13,6} \right).1,{{6.10}^{ - 19}}}} = 9,{74.10^{ - 8}}m\)
Một đám nguyên tử hidro đang ở trạng thái cơ bản. Khi chiếu bức xạ có tần số f1 vào đám nguyên tử này thì chúng phát ra tối đa 3 bức xạ. Khi chiếu bức xạ có tần số f2 vào đám nguyên tử này thì chúng phát ra tối đa 10 bức xạ. Biết năng lượng ứng với các trạng thái dừng của nguyên tử hidro được tính theo biểu thức \({E_n} = - \frac{{{E_0}}}{{{n^2}}}\), (với E0 là hằng số dương; n = 1, 2, 3,…). Tỉ số \(\frac{{{f_1}}}{{{f_2}}}\) là:
+ Chiếu f1 vào đám nguyên tử thứ nhất thì chúng phát ra tối đa 3 bức xạ nên:\(\frac{{{n_1}\left( {{n_1} - 1} \right)}}{2} = 3 \Rightarrow {n_1} = 3\)
+ Chiếu f2 vào đám nguyên tử thứ hai thì chúng phát ra tối đa 10 bức xạ nên: \(\frac{{{n_2}\left( {{n_2} - 1} \right)}}{2} = 10 \Rightarrow {n_2} = 5\)
Ta có: \(\left\{ {\begin{array}{*{20}{l}} {{\varepsilon _1} = {E_3} - {E_1} \Leftrightarrow h.{f_1} = - \frac{{{E_0}}}{{{3^2}}} - \left( { - \frac{{{E_0}}}{{{1^2}}}} \right) = \frac{8}{9}{E_0}{\mkern 1mu} {\mkern 1mu} \left( 1 \right)}\\ {{\varepsilon _2} = {E_5} - {E_1} \Leftrightarrow h.{f_2} = - \frac{{{E_0}}}{{{5^2}}} - \left( { - \frac{{{E_0}}}{{{1^2}}}} \right) = \frac{{24}}{{25}}{E_0}{\mkern 1mu} {\mkern 1mu} \left( 2 \right)} \end{array}} \right.\)
Chia hai vế của (1) cho (2) ta được: \(\frac{{{f_1}}}{{{f_2}}} = \frac{8}{9}.\frac{{25}}{{24}} = \frac{{25}}{{27}}\)
Gọi c là tốc độ ánh sáng trong chân không. Theo thuyết tương đối, một hạt có khối lượng động (khối lượng tương đối tính) là m thì nó có năng lượng toàn phần là:
Năng lượng toàn phần là: \(E = m{c^2}\)
Hạt nhân \(_3^7Li\) có khối lượng 7,0144u. Cho khối lượng của proton và notron lần lượt là 1,0073u và 1,0087u. Độ hụt khối của hạt nhân \(_3^7Li\) là:
Độ hụt khối của hạt nhân \(_3^7Li\) là: \(\Delta m = Z.{m_p} + \left( {A - Z} \right){m_n} - {m_{hn}}\)
\( \Rightarrow \Delta m = 3.1,0073 + \left( {7 - 3} \right).1,0087 - 7,0144 = 0,0423u\)
Hiện nay urani tự nhiên chứa hai đồng vị phóng xạ \(^{235}U\) và \(^{238}U\) với tỉ lệ số hạt \(^{235}U\) và số hạt \(^{238}U\) là \(\frac{7}{{1000}}\). Biết chu kì bán rã của \(^{235}U\) và \(^{238}U\) lần lượt là \(7,{00.10^8}\) năm và \(4,{50.10^9}\) năm. Cách đây bao nhiêu năm, urani tự nhiên có tỉ lệ số hạt \(^{235}U\) và số hạt \(^{238}U\) là \(\frac{3}{{100}}\)?
Gọi \({N_{01}};{N_{02}}\) lần lượt là số hạt nhân ban đầu của \(^{235}U\) và \(^{238}U\)
Hiện nay:
\(\frac{{{N_1}}}{{{N_2}}} = \frac{{{N_{01}}{{.2}^{ - \frac{{{t_2}}}{{{T_1}}}}}}}{{{N_{02}}{{.2}^{ - \frac{{{t_2}}}{{{T_2}}}}}}} = \frac{7}{{1000}}{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( 1 \right)\)
Tại thời điểm t1:
\(\frac{{{N_1}}}{{{N_2}}} = \frac{{{N_{01}}{{.2}^{ - \frac{{{t_1}}}{{{T_1}}}}}}}{{{N_{02}}{{.2}^{ - \frac{{{t_1}}}{{{T_2}}}}}}} = \frac{3}{{100}}{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( 2 \right)\)
Chia (1) cho (2) ta được:
\(\begin{array}{l} \frac{{{2^{ - \frac{{{t_2}}}{{{T_1}}}}}{{.2}^{ - \frac{{{t_1}}}{{{T_2}}}}}}}{{{2^{ - \frac{{{t_2}}}{{{T_2}}}}}{{.2}^{ - \frac{{{t_1}}}{{{T_1}}}}}}} = \frac{7}{{30}}{\mkern 1mu} \Leftrightarrow {2^{ - \frac{{{t_2}}}{{{T_1}}}}}{.2^{ - \frac{{{t_1}}}{{{T_2}}}}}{.2^{\frac{{{t_2}}}{{{T_2}}}}}{.2^{\frac{{{t_1}}}{{{T_1}}}}} = \frac{7}{{30}}\\ \Leftrightarrow \left( {{2^{ - \frac{{{t_2}}}{{{T_1}}}}}{{.2}^{\frac{{{t_1}}}{{{T_1}}}}}} \right).\left( {{2^{ - \frac{{{t_1}}}{{{T_2}}}}}{{.2}^{\frac{{{t_2}}}{{{T_2}}}}}} \right) = \frac{7}{{30}}\\ \Leftrightarrow {2^{ - \frac{{{t_2} - {t_1}}}{{{T_1}}}}}{.2^{\frac{{{t_2} - {t_1}}}{{{T_2}}}}} = \frac{7}{{30}} \Leftrightarrow {2^{\left( {{t_2} - {t_1}} \right).\left( {\frac{1}{{{T_2}}} - \frac{1}{{{T_1}}}} \right)}} = \frac{7}{{30}}\\ \Leftrightarrow \left( {{t_2} - {t_1}} \right).\left( {\frac{1}{{{T_2}}} - \frac{1}{{{T_1}}}} \right) = \ln \frac{7}{{30}} \Rightarrow \left( {{t_2} - {t_1}} \right) = \frac{{{{\log }_2}\frac{7}{{30}}}}{{\left( {\frac{1}{{{T_2}}} - \frac{1}{{{T_1}}}} \right)}} \end{array}\)
\( \Rightarrow \left( {{t_2} - {t_1}} \right) = \frac{{{{\log }_2}\frac{7}{{30}}}}{{\left( {\frac{1}{{{T_2}}} - \frac{1}{{{T_1}}}} \right)}} = 1,74{\mkern 1mu} {\mkern 1mu} \left( {ti{\mkern 1mu} nam} \right)\)
Người ta dùng hạt proton có động năng 1,6MeV bắn vào hạt nhân \(_3^7Li\) đứng yên, sau phản ứng thu được hai hạt giống nhau có cùng động năng. Giả sử phản ứng không kèm theo bức xạ γ. Biết năng lượng toả ra của phản ứng là 17,4MeV. Động năng của mỗi hạt sinh ra bằng:
Phương trình phản ứng hạt nhân\(_1^1p + _3^7Li \to _2^4He + _2^4He\)
Ta có: \(\left\{ {\begin{array}{*{20}{l}} {{K_p} = 1,6MeV}\\ {{K_{Li}} = 0}\\ {\Delta E = 17,4MeV} \end{array}} \right.\)
Năng lượng toả ra của phản ứng được xác định bởi công thức:
\(\begin{array}{l} \Delta E = \sum {{K_s}} - \sum {{K_{tr}}} = \left( {{K_{He}} + {K_{He}}} \right) - \left( {{K_{Li}} + {K_p}} \right)\\ \Leftrightarrow 17,4 = 2{K_{He}} - 1,6 \Rightarrow {K_{He}} = 9,5MeV \end{array}\)

.PNG)