Đề thi thử tốt nghiệp THPT QG môn Vật Lý năm 2020 - Tuyển chọn số 3
Đề thi thử tốt nghiệp THPT QG môn Vật Lý năm 2020
-
Hocon247
-
40 câu hỏi
-
90 phút
-
54 lượt thi
-
Dễ
Tham gia [ Hs Hocon247.com ] - Cộng Đồng Luyện Thi Trực Tuyến để được học tập những kiến thức bổ ích từ HocOn247.com
Một chất điểm dao động điều hòa với phương trình \(x = 4\cos \left( {5\pi t + \frac{{3\pi }}{4}} \right)\) cm. Biên độ dao động của chất điểm là
Biên độ dao động của chất điểm 4 cm.
Dao động cưỡng bức có
Dao động cưỡng bức có biên độ không đổi theo thời gian
Khi nói về sự phản xạ của sóng cơ trên vật cản cố định, phát biểu nào sau đây đúng?
Sóng phản xạ luôn ngược pha với sóng tới tại điểm phản xạ.
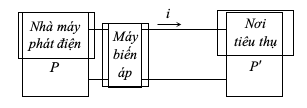
Sơ đồ của một quá trình truyền tải điện năng từ nơi sản xuất đến nơi tiêu thụ được mô tả bởi hình vẽ. Kết luận nào sau đây là đúng?
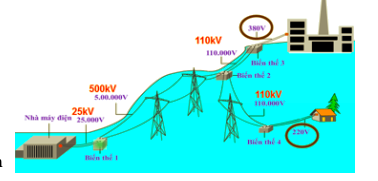
Biến thế 4 là biến thế hạ áp
Đặt điện áp \(u = U\sqrt 2 c{\rm{os}}\left( {\omega {\rm{t}}} \right)\)chỉ chứa cuộn cảm thuần có độ tự cảm L . Cường độ dòng điện hiệu dụng chạy qua cuộn cảm là
Cường độ dòng điện hiệu dụng qua cuộn cảm \(I = \frac{U}{{{Z_L}}} = \frac{U}{{L\omega }}\)
Trong chân không, ánh sáng màu vàng của quang phổ hơi natri có bước sóng bằng
Ánh sáng vàng có bước sóng vào cỡ 0,58 μm.
Điểm khác nhau cơ bản giữa hiện tượng quang điện trong và hiện tượng quang điện ngoài là electron quang điện
Hiện tượng quang điện trong thì electron bị bứt ra khỏi liên kết, còn quang điện ngoài thì electron bị bứt ra khỏi bề mặt kim loại
Một hạt nhân X có số khối A , độ hụt khối \(\Delta m\) Với c là vận tốc của ánh sáng trong chân không. Năng lượng liên kết riêng của hạt nhân này được xác định bởi biểu thức
Năng lượng liên kết riêng của hạt nhân \({\varepsilon _{lk}} = \frac{{\Delta m{c^2}}}{A}\)
Một phần đồ thị li độ – thời gian của một dao động điều hòa trên trục Ox được cho như hình vẽ. Biên độ dao động của vật là
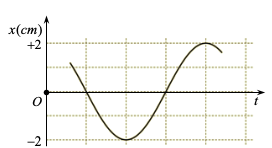
Biên độ của dao động 2 cm
Hiện tượng tự cảm là hiện tượng cảm ứng điện từ do sự biến thiên từ thông qua mạch gây ra bởi
Tự cảm là hiện tượng cảm ứng điện từ do sự biến thiên từ thông qua mạch gây bởi sự biến thiên của chính cường độ dòng điện trong mạch.
Một con lắc lò xo gồm vật nặng và lò xo có độ cứng N/m dao động điều hòa với biên độ 10 cm. Năng lượng của con lắc là
Năng lượng dao động của con lắc \(E = \frac{1}{2}k{A^2} = 0,4\) J
Một mạch dao động điện từ lí tưởng gồm cuộn cảm thuần có độ tự cảm L và tụ điện có điện dung C. Khoảng thời gian giữa hai lần liên tiếp điện áp trên tụ đạt cực đại là
Chu kì dao động của mạch LC là \(T = 2\pi \sqrt {LC} \)
Trong các dụng cụ dưới đây, dụng cụ nào có cả máy phát và máy thu vô tuyến?
Điện thoại di động có cả máy phát và máy thu sóng vô tuyến
Tia tử ngoại được ứng dụng để
Tia tử ngoại được ứng dụng để tìm vết nứt trên bề mặt các vật.
Theo mẫu nguyên tử Bo, bán kính quỹ đạo dừng ứng với trạng thái cơ bản của nguyên tử hiđrô là r0 . Khi electron chuyển động trên quỹ đạo dừng M thì bán kính quỹ đạo của nó là:
Bán kính quỹ đạo dừng của electron \({r_n} = {n^2}{r_0}\), quỹ đạo dừng M ứng với n = 3 → \(% MathType!MTEF!2!1!+- {r_M} = 9{r_0}\)
Gọi A1, A2 ,A3 lần lượt là công thoát electron khỏi đồng, kẽm, canxi. Giới hạn quang điện của đồng, kẽm, can xi lần lượt là 0,3 µm, 0,35 µm, 0,45 µm. Kết luận nào sau đây đúng?
Công thoát tỉ lệ nghịch với giới hạn quang điện, do vậy với \({\lambda _1} > {\lambda _2} > {\lambda _3}\) → \({A_3} < {A_2} < {A_1}\)
So với hạt nhân \(_{27}^{60}Co\) , hạt nhân \(_{84}^{210}Po\) có nhiều hơn
So với hạt nhân \(_{27}^{60}Co\), hạt nhân \(_{84}^{210}Po\) có nhiều hơn 57 proton và 93 notron.
Cho phản ứng hạt nhân A -> B + C . Gọi mA, mB và mC lần lượt là khối lượng của các hạt nhân A, B, C. Phản ứng tỏa năng lượng khi
Phản ứng là tỏa năng lượng khi \({m_A} > {m_B} + {m_C}\)
Một đoạn dây dẫn chuyển động với vận tốc v trong một từ trường đều B , điện tích xuất hiện ở hai đầu của đoạn dây do hiện tượng cảm ứng điện từ được biểu diễn như hình vẽ. Cảm ứng từ có
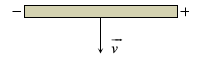
Đầu trái của dây dẫn tích điện âm → đầu này thừa electron → Lực Lo – ren – xo tác dụng lên các electron tự do có chiều từ phải sâng trái.
→ Áp dụng quy tắc bàn tay trái → cảm ứng từ có phương thẳng đứng, hướng vào trong mặt phẳng hình vẽ.
Nam châm không tác dụng lên
Nam châm không tác dụng lên điện tích đứng yên (không có từ tính).
Đồ thị li độ – thời gian của hai dao động điều hòa cùng tần số được cho như hình vẽ. Phương trình dao động tổng hợp của chúng là
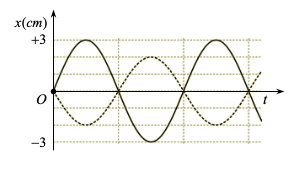
+ Từ đồ thị, ta thu được phương trình của hai dao động thành phần:
\(\left\{ \begin{array}{l} {x_1} = 3\cos \left( {\frac{\pi }{2}t - \frac{\pi }{2}} \right)\\ {x_2} = 2\cos \left( {\frac{\pi }{2}t + \frac{\pi }{2}} \right) \end{array} \right.\)cm → \(x = {x_1} + {x_2} = \cos \left( {\frac{\pi }{2}t - \frac{\pi }{2}} \right)\)cm.
Một con lắc đơn dao động điều hòa với biên độ góc 0,1 rad ở một nơi có gia tốc trọng trường là m/s2. Vào thời điểm vật qua vị trí có li độ dài 8 cm thì vật có vận tốc \(20\sqrt 3 \)cm/s. Chiều dài dây treo con lắc là
Ta có:
\({\left( {\frac{s}{{{s_0}}}} \right)^2} + {\left( {\frac{v}{{{v_0}}}} \right)^2} = 1\) → \({\left( {\frac{s}{{l{\alpha _0}}}} \right)^2} + {\left( {\frac{v}{{\sqrt {gl} {\alpha _0}}}} \right)^2} = 1\)→ l = 1,6 m.
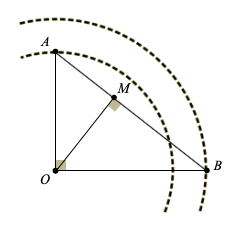
Nguồn âm (coi như một điểm) đặt tại đỉnh A của tam giác vuông ABC \((\widehat {{A_{}}} = {90^0})\) . Tại B đo được mức cường độ âm là L1= 50,0 dB. Khi di chuyển máy đo trên cạnh huyền BC từ B tới C người ta thấy : thoạt tiên mức cường độ âm tăng dần tới giá trị cực đại L2 = 60 dB sau đó lại giảm dần. Bỏ qua sự hấp thụ âm của môi trường. Mức cường độ âm tại C là
Khi máy đo di chuyển trên BC thì mức cường độ âm lớn nhất tại H, với H là hình chiếu của A lên BC .
Ta có
\(\frac{{AB}}{{AH}} = {10^{\frac{{\Delta L}}{{20}}}} = \sqrt {10} \), chọn AH = 1 → \(AB = \sqrt {10} \)
Áp dụng hệ thức lượng trong tam giác vuông
\(\frac{1}{{A{B^2}}} = \frac{1}{{A{H^2}}} + \frac{1}{{A{C^2}}}\) → \(AC = \frac{{\sqrt {10} }}{3}\)
→ Mức cường độ âm tại C: \({L_C} = {L_H} - 20\log \frac{{AC}}{{AH}} = 60 - 20\log \frac{{\sqrt {10} }}{3} = 59,5\)dB
Đặt điện áp xoay chiều có giá trị hiệu dụng không đổi và tần số f thay đổi được vào hai bản tụ điện. Khi f = 60Hz thì cường độ dòng điện hiệu dụng qua tụ điện bằng 0,5 A. Để cường độ dòng điện hiệu dụng qua tụ điện bằng 8 A thì tần số f' bằng
Ta có
\(I = \frac{U}{{{Z_C}}} = U2\pi fC\) -> \(\left\{ \begin{array}{l} 0,5 = U2\pi C.60\\ 8 = U2\pi C.f' \end{array} \right.\)
=> \(f' = 960\) Hz
Mạch dao động gồm cuộn cảm thuần có độ tự cảm L = 5 mH và tụ điện có C = 2 µF. Điện áp hai bản tụ điện có biểu thức \(u = 2\cos \left( {\omega t} \right)\)V. Từ thông cực đại qua cuộn cảm là
+ Với mạch dao động LC ta có: \(\frac{1}{2}LI_0^2 = \frac{1}{2}CU_0^2\)→ \(I = \sqrt {\frac{C}{L}} {U_0} = 0,04\)A.
→ Từ thông tự cảm cực đại \({\Phi _0} = L{I_0} = {2.10^{ - 4}}\)Wb.
Đặt điện áp \(u = 100\sqrt 2 \cos \left( {{\rm{100}}\pi t} \right)\) vào hai đầu đoạn mạch mắc nối tiếp gồm điện trở thuần R, cuộn cảm thuần có độ tự cảm L và tụ điện có điện dung C thay đổi được. Thay đổi C để điện áp hiệu dụng giữa hai bản tụ điện đạt cực đại; khi đó điện áp hiệu dụng ở hai đầu cuộn cảm là UL = 97,5V. So với điện áp hai đầu đoạn mạch thì điện áp hai đầu điện trở thuần:
+ Khi C biến thiên để Uc cực đại thì điện áp hai đầu đoạn mạch vuông pha với điện áp hai đầu đoạn mạch RL
+ Từ hình vẽ, ta có :
\({U^2} = {U_{Cmax}}\left( {{U_{Cmax}} - {U_L}} \right)\)
→ \({100^2} = {U_{Cmax}}\left( {{U_{Cmax}} - 97,5} \right)\)→ \({U_{Cmax}} = 160\)V.
\(\sin \varphi = \frac{{{U_C} - {U_L}}}{U} = 0,625\) → \(\varphi = 0,22\pi \)
→ Vậy điện áp hai đầu điện trở sớm pha hơn điện áp hai đầu đoạn mạch một góc\(\varphi = 0,22\pi \) rad.
Chiết suất của thủy tinh phụ thuộc vào bước sóng ánh sáng theo công thức \(n = 1,26 + \frac{{7,{{555.10}^{ - 4}}}}{{{\lambda ^2}}}\) với \(\lambda \) là bước sóng trong chân không, đo bằng mét. Chiếu chùm sáng hẹp gồm hai màu đỏ và tím (màu đỏ có bước sóng 0,76 µm và tím có bước sóng 0,38 µm) từ không khí vào thủy tinh với góc tới 450. Góc giữa tia đỏ và tia tím trong thủy tinh là
+ Áp dụng định luật khúc xạ ánh sáng
\({n_1}\sin i = {n_2}\sin r\)
→ \(\left\{ \begin{array}{l} \sin \left( {{{45}^0}} \right) = \left[ {1,26 + \frac{{7,{{555.10}^{ - 14}}}}{{{{\left( {0,{{76.10}^{ - 6}}} \right)}^2}}}} \right]\sin {r_d}\\ \sin \left( {{{45}^0}} \right) = \left[ {1,26 + \frac{{7,{{555.10}^{ - 14}}}}{{{{\left( {0,{{38.10}^{ - 6}}} \right)}^2}}}} \right]\sin {r_t} \end{array} \right.\)
→\(\left\{ \begin{array}{l} {r_d} = {30^0}33'30,48''\\ {r_t} = {23^0}21'43'' \end{array} \right.\)
→ \(\Delta r = {7^0}11'47''\)
Trong thí nghiệm giao thoa ánh sáng đơn sắc với khe Y – âng, khoảng cách từ hai khe đến màn là 2 m. Trên màn, tại điểm M cách vân sáng trung tâm 6 mm có vân sáng bậc 5. Khi thay đổi khoảng cách giữa hai khe một đoạn bằng 0,2 mm sao cho vị trí vân sáng trung tâm không thay đổi thì tại M có vận sáng bậc 6. Giá trị của bước sóng là
+ Theo giả thuyết bài toán, ta có:
\({x_S} = k\frac{{D\lambda }}{a}\)→ \(\left\{ \begin{array}{l} {6.10^{ - 3}} = 5\frac{{D\lambda }}{a}\\ {6.10^{ - 3}} = 6\frac{{D\lambda }}{{a + 0,{{2.10}^{ - 3}}}} \end{array} \right.\)
→ \(\frac{5}{a} = \frac{6}{{a + 0,{{2.10}^{ - 3}}}}\)
→ a = 1 mm và \(\lambda = 0,6\) μm
Theo mẫu nguyên tử của Bo, bán kính quỹ đạo dừng ứng với trạng thái cơ bản của nguyên tử Hiđro là \({r_0} = 0,{53.10^{ - 10}}\) m và năng lượng của nguyên tử ứng với các trạng thái dừng được xác định bằng biểu thức \({E_n} = \frac{{ - 13,6}}{{{n^2}}}\)eV, với n = 1, 2, 3…. Một đám nguyên tử Hiđro đang ở trạng thái kích thích ứng với bán kính quỹ đạo dừng là 1,908 nm. Tỉ số giữa phôtôn có năng lượng lớn nhất và phôtôn có năng lượng nhỏ nhất có thể phát ra là
Bán kính quỹ đạo dừng của electron theo mẫu nguyên tử Bo:
\({r_n} = {n^2}{r_0}\)→ \(n = \sqrt {\frac{{{r_n}}}{{{r_0}}}} = \sqrt {\frac{{1,{{908.10}^{ - 9}}}}{{0,{{53.10}^{ - 10}}}}} = 6\)
Photon có năng lượng lớn nhất ứng với sự chuyển mức từ 6 về 1, photon có năng lượng bé nhất ứng với sự chuyển mức từ 6 về 5, ta có tỉ số
\(\frac{{{\varepsilon _{ma{\rm{x}}}}}}{{{\varepsilon _{\min }}}} = \frac{{ - \left( {\frac{1}{{{6^2}}} - \frac{1}{{{1^2}}}} \right)}}{{ - \left( {\frac{1}{{{6^2}}} - \frac{1}{{{5^2}}}} \right)}} = \frac{{875}}{{11}}\)
Một nhà máy phát điện hạt nhân có công suất phát điện là 1000 MW và hiệu suất 25% sử dụng các thanh nhiên liệu đã được làm giàu \(_{92}^{235}U\) đến 35% (khối lượng \(_{92}^{235}U\) chiếm 35% khối lượng thanh nhiên liệu). Biết rằng trung bình mỗi hạt nhân \(_{92}^{235}U\) phân hạch tỏa ra 200 MeV cung cấp cho nhà máy. Cho \({N_A} = 6,{022.10^{23}}\) mol–1. Khối lượng các thanh nhiên liệu cần dùng trong một năm (365 ngày) là
Năng lượng mà nhà máy tạo ra được trong 1 năm : \(E = Pt = 3,{1536.10^6}\)J.
Với hiệu suất 0,25 thì năng lượng thực tế nhà máy này thu được từ phản ưng phân hạch là
\({E_0} = \frac{E}{{25}}100 = 1,{26144.10^{17}}\)J.
Số phản ứng phân hạch tương ứng : \(n = \frac{{{E_0}}}{{\Delta E}} = \frac{{1,{{26144.10}^{17}}}}{{{{200.10}^6}.1,{{6.10}^{ - 19}}}} = 3,{942.10^{27}}\)
Khối lượng Urani tương ứng \(m = \mu A = \frac{n}{{{N_A}}}A = 1538\)kg.
→ Vậy khối lượng nhiên liệu là \({m_0} = \frac{m}{{35}}100 \approx 4395\)kg.
Ban đầu có một lượng chất phóng xạ X nguyên chất. Ở thời điểm t1, trong mẫu chất phóng xạ có 60% số hạt nhân bị phân rã. Đến thời điểm\({t_2} = {t_1} + 36\)ngày số hạt nhân chưa bị phân rã còn 2,5% so với số hạt nhân ban đầu. Chu kì bán rã của X là
+ Ta có
\(\left\{ \begin{array}{l} \Delta {N_{{t_1}}} = 0,6{N_0} = {N_0}\left( {1 - {2^{ - \frac{{{t_1}}}{T}}}} \right)\\ {N_{{t_2}}} = 0,025{N_0} = {N_0}{2^{ - \frac{{{t_1} + 36}}{T}}} = {N_0}{2^{ - \frac{{{t_1}}}{T}}}{.2^{ - \frac{{36}}{T}}} \end{array} \right.\)→\(\left\{ \begin{array}{l} {2^{ - \frac{{{t_1}}}{T}}} = 0,4\\ 0,025 = 0,{42^{ - \frac{{36}}{T}}} \end{array} \right.\) → T = 9 ngày
Một nguồn sóng điểm O tại mặt nước dao động điều hòa theo phương thẳng đứng với tần số 10 Hz. Tốc độ truyền sóng trên mặt nước là 40 cm/s. Gọi A và B là hai điểm tại mặt nước có vị trí cân bằng cách O những đoạn 12 cm và 16 cm mà OAB là tam giác vuông tại O. Tại thời điểm mà phần tử tại O ở vị trí cao nhất thì trên đoạn AB có mấy điểm mà phần tử tại đó đang ở vị trí cân bằng ?
Bước sóng của sóng \(\lambda = \frac{v}{f} = \frac{{40}}{{10}} = 4\)cm.
+ Ta để ý rằng \(\left\{ \begin{array}{l} \frac{{OA}}{\lambda } = \frac{{12}}{4} = 3\\ \frac{{OB}}{\lambda } = \frac{{16}}{4} = 4 \end{array} \right.\)
→ Tại thời điểm O ở vị trí cao nhất (đỉnh gợn sóng) thì A và B là các định của những gợn thứ 3 và thứ 4.
+ Áp dụng hệ thức lượng trong tam giác vuông
\(\frac{1}{{O{A^2}}} + \frac{1}{{O{B^2}}} = \frac{1}{{O{M^2}}}\)↔ \(\frac{1}{{{{12}^2}}} + \frac{1}{{{{16}^2}}} = \frac{1}{{O{M^2}}}\) → OM = 9,6cm.
→ Khi O là đỉnh cực đại thì trên AB chỉ có đỉnh thứ 3 và thứ 4 đi qua.
+ Ta để ý rằng đỉnh sóng thứ hai có bán kính 2.4 = 8 cm, giữa hai sóng liên tiếp có hai dãy phần tử đang ở vị trí cân bằng cách đỉnh \(0,25\lambda \)và \(0,75\lambda \)→ dãy các phần tử đang ở vị trí cân bằng nằm giữa đỉnh thứ hai và thứ 3 cách O lần lượt là 8 + 1 = 9 cm và 8 + 1 + 2 = 11 cm. → trên AB chỉ có dãy phần tử ứng với bán kính 11 cm đi qua.
+ Giữa hai đỉnh sóng thứ 3 và thứ 4 có hai dãy phần tử môi trường đang ở vị trí cân bằng.
→ Có tất cả 4 vị trí phần tử môi trường đang ở vị trí cân bằng.
Trong thí nghiệm khe Y – âng ta thu được hệ thống vân sáng, vân tối trên màn. Xét hai điểm A, B đối xứng qua vân trung tâm, khi màn cách hai khe một khoảng là D thì A, B là vân sáng. Dịch chuyển màn ra xa hai khe một khoảng d thì A, B là vân sáng và đếm được số vân sáng trên đoạn AB trước và sau dịch chuyển màn hơn kém nhau 4. Nếu dịch tiếp màn ra xa hai khe một khoảng 9d nữa thì A, B là vân sáng và nếu dịch tiếp màn ra xa nữa thì tại A và B không còn xuất hiện vẫn sang nữa. Tại A khi chưa dịch chuyển màn là vân sáng thứ mấy?
+ Giả sử ban đầu là vị trí cho vân sáng bậc k → \({x_M} = k\frac{{D\lambda }}{a}\)
Khi dịch chuyển mà ra xa một đoạn thì vẫn là vân sáng nhưng số vân sáng trên giảm đi 4 vân điều này chứng tỏ tại lúc này là vân sáng bậc k - 2 → \({x_M} = \left( {k - 2} \right)\frac{{\left( {D + d} \right)\lambda }}{a}\)→ \(k = \left( {k - 2} \right)\left( {1 + \frac{d}{D}} \right)\) (*).
+ Tiếp tục dịch chuyển màn ra xa thêm một khoảng 9d nữa thì A là vân sáng, sau đó nếu dịch chuyển màn tiếp tục ra xa thì ta sẽ không thu được vân sáng → lúc này A là vân sáng bậc nhất → \({x_M} = \frac{{\left( {D + 10d} \right)\lambda }}{a}\)
→ \(kD = D + 10d\)→ \(\frac{d}{D} = \frac{{k - 1}}{{10}}\)
+ Thay vào phương trình (*) ta thu được \(\frac{{{k^2}}}{{10}} - \frac{3}{{10}}k - \frac{9}{5} = 0\) → k = 6
Một vật sáng cho ảnh qua thấu kính hội tụ L, ảnh này hứng trên một màn E đặt cách vật một khoảng 1,8 m. Ảnh thu được cao gấp 0,2 lần vật. Tiêu cự của thấu kính là:
+ Ảnh hứng được trên màn → thấu kính là hội tụ, ảnh là thật → ngược chiều với vật.
+ Ta có hệ :
\(\left\{ \begin{array}{l} d + d' = 1,8\\ k = - \frac{{d'}}{d} = - 0,2 \end{array} \right.\)→ \(\left\{ \begin{array}{l} d = 1,5\\ d' = 0,3 \end{array} \right.\)m.
→ Áp dụng công thức thấu kính \(\frac{1}{d} + \frac{1}{{d'}} = \frac{1}{f}\) ↔ \(\frac{1}{{1,5}} + \frac{1}{{0,3}} = \frac{1}{f}\)→ f = 25 cm
Một con lắc lò xo thẳng đứng gồm lò xo nhẹ có độ cứng k = 25N/m một đầu được gắn với hòn bi nhỏ có khối lượng m = 100g. Khi vật đang ở vị trí cân bằng, tại thời điểm t = 0 người ta thả cho con lắc rơi tự do sao cho trục lò xo luôn nằm theo phương thẳng đứng và vật nặng ở phía dưới lò xo. Đến thời điểm \({t_1} = 0,02\sqrt {15} \) s thì điểm chính giữa của lò xo đột ngột bị giữ lại cố định. Bỏ qua ma sát, lực cản. Tốc độ của hòn bi tại thời điểm \({t_2} = {t_1} + 0,07\)s có độ lớn gần nhất với giá trị nào sau đây?
Ban đầu lò xo giãn một đoạn \(\Delta {l_0}\) , sau khoảng thời gian thả rơi lò xo và vật → lò xo co về trạng thái không biến dạng. Khi ta giữ cố định điểm chính giữa của lò xo, con lắc sẽ dao động quanh vị trí cân bằng mới.
+ Khi giữ cố định điểm chính giữa của lò xo, phần lò xo tham gia vào dao động có độ cứng \(k = 2{k_0} = 50\)N/m.
→ Tần số góc của dao động \(\omega = \sqrt {\frac{k}{m}} = \sqrt {\frac{{50}}{{0,1}}} c = 10\sqrt 5 \)rad/s → T = 0,28s.
→ Độ biến dạng của lò xo tại vị trí cân bằng mới \(\Delta l = \frac{{mg}}{k} = \frac{{0,1.10}}{{50}} = 2\)cm.
+ Vận tốc của con lắc tại thời điểm t1 là \({v_0} = g{t_1} = 10.0,02\sqrt {15} = 0,2\sqrt {15} \) m/s.
→ Biên độ dao động của con lắc \(A = \sqrt {\Delta {l^2} + {{\left( {\frac{{{v_0}}}{\omega }} \right)}^2}} = \sqrt {{2^2} + {{\left( {\frac{{20\sqrt {15} }}{{10\sqrt 5 }}} \right)}^2}} = 4\) cm.
+ Ta chú ý rằng tại thời điểm t1 vật ở vị trí có li độ \(\left| x \right| = \frac{A}{2} = 2\) cm → sau khoảng thời gian \(\Delta t = {t_2} - {t_1} = \frac{T}{4} = 0,07\) s vật đi vị trí có li độ \(\left| x \right| = \frac{{\sqrt 3 }}{2}A\)→ \(v = \frac{{{v_{max}}}}{2} = \frac{{\omega A}}{2} = \frac{{4.10\sqrt 5 }}{2} = 20\sqrt 5 \approx 44,7\)cm/s
Sóng dừng trên một sợi dây có biên độ ở bụng là 40 mm. Xét hai phần tử M ,N trên dây có biên độ \(20\sqrt 3\)mm, vị trí cân bằng riêng cách nhau 5 cm, người ta nhận thấy giữa M và N các phần tử dây luôn dao động với biên độ nhỏ hơn \(20\sqrt 3\)mm. Bước sóng của sóng truyền trên dây là
Ta có:
o \({a_M} = {a_N} = \frac{{\sqrt 3 }}{2}{A_b} = 20\sqrt 3 \) mm → M và N cách nút một đoạn \(\frac{\lambda }{6}\).
o giữa M và N các điểm dao động với biên độ nhỏ hơn biên độ của M, N → M và N nằm hai bên một nút sóng.
→ \(MN = \frac{\lambda }{6} + \frac{\lambda }{6} = 5\) cm → \(\lambda = 15\)cm
Ở mặt thoáng của chất lỏng có hai nguồn sóng A, B cách nhau 18 cm, dao động theo phương thẳng đứng với phương trình \({u_A} = {u_B} = a\cos \left( {20\pi t} \right)\) (t tính bằng giây). Tốc độ truyền sóng trên mặt chất lỏng là 50 cm/s. Gọi M là điểm ở mặt chất lỏng gần A nhất sao cho phần tử chất lỏng tại M dao động với biên độ cực đại và cùng pha với nguồn A. Khoảng cách AM là
+ Áp dụng kết quả bài toán điều kiện để một vị trí cực đại và cùng pha với nguồn
\(\left\{ \begin{array}{l} {d_2} - {d_1} = k\lambda \\ {d_2} + {d_1} = n\lambda \end{array} \right.(1)\)với n, k có độ lớn cùng chẵn hoặc cùng lẽ
+ Số dãy dao động với biên độ cực đại
\(\left\{ \begin{array}{l} {d_2} - {d_1} = k\lambda \\ {d_2} + {d_1} = n\lambda \end{array} \right.(1)\)→ \( - \frac{{18}}{5} < k < \frac{{18}}{5}\)→ \( - 3,6 < k < 3,6\)
+ Để M gần A nhất thì khi đó M phải nằm trên cực đại ứng với , áp dụng kết quả ta có:
\(\left\{ \begin{array}{l} {d_2} - {d_1} = 3\lambda \\ {d_2} + {d_1} = n\lambda \end{array} \right.\) ↔ \(n = 3 + \frac{{2{d_1}}}{\lambda }\) chú ý rằng n là một số lẻ
+ Mặc khác từ hình vẽ ta có thể xác định được giá trị nhỏ nhất của d1 như sau
\(\left\{ \begin{array}{l} {d_2} - {d_{1\min }} = 15\\ {d_2} + {d_{1in}} = 18 \end{array} \right.\)→ \(2{{\rm{d}}_{1\min }} = 3\)
Thay vào biểu thức trên ta thu được \(n \ge 3 + \frac{{2{{\rm{d}}_{1\min }}}}{\lambda } = 3 + \frac{3}{5} = 3,6\)
→ Vậy số lẻ gần nhất ứng với n = 5 .
Thay trở lại phương trình (1) ta tìm được d1 = 5 cm.
Xét một đoạn mạch xoay chiều mắc nối tiếp gồm cuộn dây D và tụ điện C. Điện áp tức thời ở hai đầu cuộn dây D và điện áp tức thời ở hai đầu tụ điện C được biểu diễn bởi các đồ thị uD , như hình vẽ. Trên trục thời gian t , khoảng cách giữa các điểm a – b, b – c, c – d, d – e là đều nhau. Điện áp hiệu dụng ở hai đầu đoạn mạch gần bằng với giá trị nào nhất sau đây?
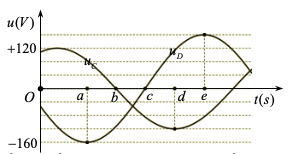
Ta gọi các khoảng thời gian a – b, b – c, c – d, d – e là . Từ đồ thị ta thấy:
o các điện áp biển đổi với chu kì T = 8t
o khoảng thời gian kể từ khi uDmin đến uCmin gần nhất là \(\Delta t = 3t\).
→ Độ lệch pha giữa hai dao động \(\Delta \varphi = \frac{{\Delta t}}{T}{360^0} = {135^0}\)
+ Mặc khác U0C=120 V và U0D=160V → \(U = \frac{{\sqrt {U_{0D}^2 + U_{0C}^2 + 2{U_{0D}}{U_{0C}}\cos \Delta \varphi } }}{{\sqrt 2 }} \approx 80\) V
Trên đường dây người ta tăng điện áp ở nơi truyền đi bằng máy tăng áp lí tưởng có tỉ số giữa số vòng dây của cuộn thứ cấp và số vòng dây của cuộn sơ cấp là k. Biết công suất của nhà máy điện không đổi, điện áp hiệu dụng giữa hai đầu cuộn sơ cấp không đổi, hệ số công suất của mạch điện bằng 1. Khi k = 10 thì công suất hao phí trên đường dây bằng 10% công suất ở nơi tiêu thụ. Để công suất hao phí trên đường dây bằng 5% công suất ở nơi tiêu thụ thì k phải có giá trị là
Phương trình truyền tải điện năng \(P = \Delta P + {P_{tt}}\) , với P, \(\Delta P\) và Ptt lần lượt là công suất truyền đi, công suất hao phí và công suất nơi tiêu thụ.
Ta có
\(\left\{ \begin{array}{l} \Delta P = 0,1P'\\ \Delta P = 0,05P' \end{array} \right.\)→ \(\left\{ \begin{array}{l} \Delta P = \frac{P}{{11}} = \frac{{{P^2}R}}{{{U^2}}}\\ \Delta P = \frac{P}{{21}} = \frac{{{P^2}R}}{{{k^2}{U^2}}} \end{array} \right.\)
+ Lập tỉ số → \(\frac{{{k^2}}}{{{{10}^2}}} = \frac{{21}}{{11}}\)→ k = 13,8.
Một sóng điện từ lan truyền trong chân không dọc theo đường thẳng từ điểm M đến điểm N cách nhau 45 m. Biết sóng này có thành phần điện trường tại mỗi điểm biến thiên điều hòa theo thời gian với tần số 5 MHz. Lấy \(c = {3.10^8}\)m/s. Ở thời điểm t, cường độ điện trường tại M bằng 0. Thời điểm nào sau đây cường độ điện trường tại N bằng 0 là
+ Chu kì dao động của điện từ trường \(T = \frac{1}{f} = \frac{1}{{{{5.10}^6}}} = {2.10^{ - 7}}\)s.
Thời gian để sóng truyền đi từ M đến N là \(\Delta t = \frac{{MN}}{c} = \frac{{45}}{{{{3.10}^8}}} = 1,{5.10^{ - 7}}\)s.
+ Tại thời điểmt = 0 , cường độ điện trường tại M bằng 0, sau khoảng thời gian \(\Delta t = \frac{3}{4}T\) sóng truyền tới N→ dễ thấy rằng cần ít nhất \(\frac{T}{4} = {50.10^{ - 9}}\)s nữa điện trường tại N sẽ bằng 0.

