Ôn tập chương 5
I. Sơ đồ Ôn tập chương 5
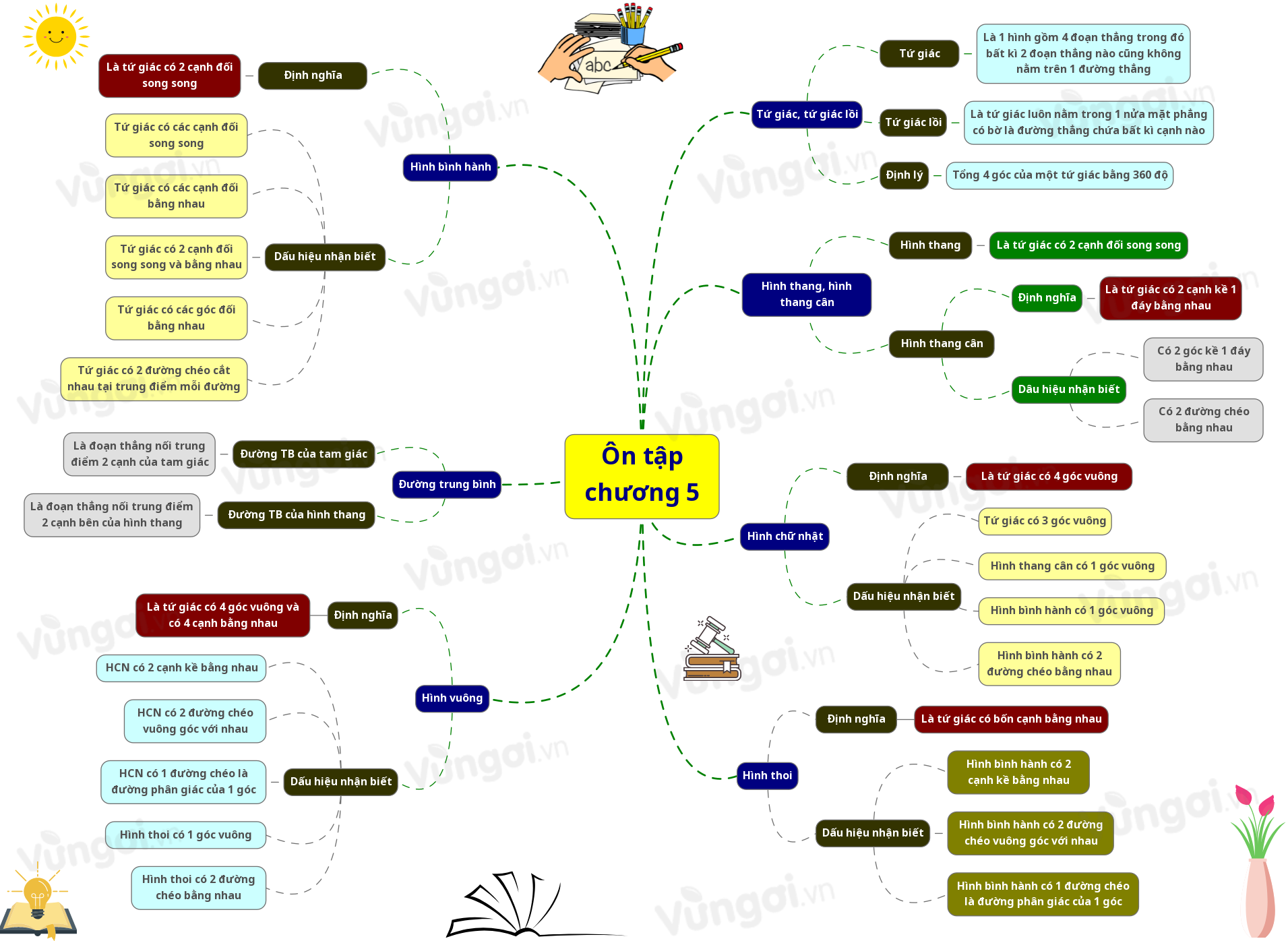
II. Ôn tập chương 5: Tứ giác
1. Tứ giác, tứ giác lồi
Định nghĩa
+ Tứ giác $ABCD$ là một hình gồm bốn đoạn thẳng $AB$ , $BC$ , $CD$ , $DA$ trong đó bất kỳ hai đoạn thẳng nào cũng không cùng nằm trên một đường thẳng.
+ Tứ giác lồi là tứ giác luôn nằm trong một nửa mặt phẳng có bờ là đường thẳng chứa bất kỳ cạnh nào
Chú ý:
Đa giác đều là đa giác có tất cả các cạnh bằng nhau và tất cả các góc bằng nhau.
Định lý tổng các góc của một tứ giác
Định lý : Tổng bốn góc của một tứ giác bằng ${360^0}$ .
2. Hình thang, hình thang cân
a. Hình thang
Định nghĩa: Hình thang là tứ giác có hai cạnh đối song song.
Hai góc kề một cạnh bên của hình thang có tổng bằng ${180^0}$
Nhận xét:
+ Nếu một hình thang có hai cạnh bên song song thì hai cạnh bên bằng nhau, hai cạnh đáy bằng nhau.
+ Nếu một hình thang có hai cạnh đáy bằng nhau thì hai cạnh bên song song và bằng nhau.
+ Hình thang vuông là hình thang có một góc vuông.
b. Hình thang cân
Định nghĩa: Hình thang cân là hình thang có hai góc kề một đáy bằng nhau.
Tính chất:
+ Trong hình thang cân, hai cạnh bên bằng nhau.
+ Trong hình thang cân, hai đường chéo bằng nhau.
Dấu hiệu nhận biết:
+ Hình thang có hai góc kề một đáy bằng nhau là hình thang cân.
+ Hình thang có hai đường chéo bằng nhau là hình thang cân.
3. Đường trung bình
a. Đường trung bình của tam giác
Định nghĩa: Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.
Định lý 1: Đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm cạnh thứ ba.
Định lý 2: Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.
b. Đường trung bình của hình thang
Định nghĩa: Đường trung bình của hình thang là đoạn thẳng nối trung điểm hai cạnh bên của hình thang.
Định lí 3: Đường thẳng đi qua trung điểm một cạnh bên của hình thang và song song với hai đáy thì đi qua trung điểm cạnh bên thứ hai.
Định lí 4: Đường trung bình của hình thang thì song song với hai đáy và bằng nửa tổng hai đáy.
4. Đối xứng trục
Định nghĩa: Hai điểm $A,B$ gọi là đối xứng với nhau qua đường thẳng $d$ nếu $d$ là đường trung trực của đoạn thẳng nối hai điểm đó.
Hai hình đối xứng qua một đường thẳng
Định nghĩa: Hai hình gọi là đối xứng với nhau qua đường thẳng $d$ nếu mỗi điểm thuộc hình này đối xứng với một điểm thuộc hình kia qua đường thẳng $d$ và ngược lại. Đường thẳng $d$ gọi là trục đối xứng của hai hình đó
Hình có trục đối xứng
Đường thẳng $d$ gọi là trục đối xứng của hình $H$ nếu điểm đối xứng với mỗi điểm thuộc hình $H$ qua đường thẳng $d$ cũng thuộc hình $H$ . Ta nói hình $H$ có trục đối xứng.
5. Hình bình hành
Định nghĩa: Hình bình hành là tứ giác có các cạnh đối song song .
Tính chất:
Trong hình bình hành:
+ Các cạnh đối bằng nhau
+ Các góc đối bằng nhau
+ Hai đường chéo cắt nhau tại trung điểm của mỗi đường
Dấu hiệu nhận biết:
+ Tứ giác có các cạnh đối song song là hình bình hành
+ Tứ giác có các cạnh đối bằng nhau là hình bình hành.
+ Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành.
+ Tứ giác có các góc đối bằng nhau là hình bình hành.
+ Tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường là hình bình hành.
6. Đối xứng tâm
Hai điểm đối xứng qua một điểm
Định nghĩa: Hai điểm $A$ , $B$ gọi là đối xứng với nhau qua điểm $O$ nếu $O$ là trung điểm của đoạn thẳng nối hai điểm đó.
Hai hình đối xứng qua một điểm
Hai hình gọi là đối xứng với nhau qua điểm $O$ nếu mỗi điểm thuộc hình này đối xứng với mỗi điểm thuộc hình kia qua điểm $O$ và ngược lại. Điểm $O$ gọi là tâm đối xứng của hai hình đó.
Hình có tâm đối xứng
Định nghĩa: Điểm $O$ gọi là tâm đối xứng của hình $H$ nếu điểm đối xứng với mỗi điểm thuộc hình $H$ qua điểm $O$ cũng thuộc hình $H$ . Ta nói hình $H$ có tâm đối xứng.
Định lý: Giao điểm hai đường chéo của hình bình hành là tâm đối xứng của hình bình hành đó.
Chú ý: Nếu hai đoạn thẳng (góc, tam giác) đối xứng với nhau qua một điểm thì chúng bằng nhau.
7. Hình chữ nhật
Định nghĩa: Hình chữ nhật là tứ giác có bốn góc vuông.
Chú ý: Hình chữ nhật cũng là một hình bình hành, một hình thang cân.
Tính chất:
+ Hình chữ nhật có tất cả các tính chất của hình hành, của hình thang cân.
- Hai cạnh đối song song, hai cạnh đối bằng nhau, hai góc đối bằng nhau
- Hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường.
Dấu hiệu nhận biết
+ Tứ giác có ba góc vuông là hình chữ nhật
+ Hình thang cân có một góc vuông là hình chữ nhật.
+ Hình bình hành có một góc vuông là hình chữ nhật
+ Hình bình hành có hai đường chéo bằng nhau là hình chữ nhật.
Áp dụng vào tam giác
Định lí:
Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền.
Nếu một tam giác có đường trung tuyến ứng với một cạnh bằng nửa cạnh ấy thì tam giác đó là tam giác vuông.
8. Hình thoi
Định nghĩa: Hình thoi là tứ giác có bốn cạnh bằng nhau.
Tính chất: Hình thoi có tất cả các tính chất của hình bình hành
+ Các cạnh đối song song, các góc đối bằng nhau
+ Hai đường chéo giao nhau tại trung điểm mỗi đường.
Định lý: Trong hình thoi:
+ Hai đường chéo vuông góc với nhau.
+ Hai đường chéo là các đường phân giác của các góc của hình thoi.
Dấu hiệu nhận biết
+ Tứ giác có bốn cạnh bằng nhau là hình thoi.
+ Hình bình hành có hai cạnh kề bằng nhau là hình thoi.
+ Hình bình hành có hai đường chéo vuông góc với nhau là hình thoi..
+ Hình bình hành có một đường chéo là đường phân giác của một góc là hình thoi.
9. Hình vuông
Định nghĩa: Hình vuông là tứ giác có bốn góc vuông và có bốn cạnh bằng nhau.
Nhận xét 1:
+ Hình vuông là hình chữ nhật có bốn cạnh bằng nhau.
+ Hình vuông là hình thoi có một góc vuông.
Như vậy, hình vuông vừa là hình chữ nhật, vừa là hình thoi.
Tính chất:
+ Hình vuông có tất cả các tính chất của hình chữ nhật và hình thoi.
+ Đường chéo của hình vuông vừa bằng nhau vừa vuông góc với nhau
Dấu hiệu nhận biết
+ Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông.
+ Hình chữ nhật có hai đường chéo vuông góc với nhau là hình vuông
+ Hình chữ nhật có một đường chéo là đường phân giác của một góc là hình vuông
+ Hình thoi có một góc vuông là hình vuông
+ Hình thoi có hai đường chéo bằng nhau là hình vuông
Nhận xét 2:
Một tứ giác vừa là hình chữ nhật, vừa là hình thoi thì tứ giác đó là hình vuông.
